数控车床主轴热变形检测及回转精度评定
李 艳 梁 亮 李英浩 高 峰
西安理工大学教育部数控机床及机械制造装备集成重点实验室,西安,710048
数控车床主轴热变形检测及回转精度评定
李艳梁亮李英浩高峰
西安理工大学教育部数控机床及机械制造装备集成重点实验室,西安,710048
针对主轴回转热误差包含的多种误差分量,采用双向正交法测量了不同转速温度场下数控车床主轴热变形所引起的回转误差。以复向量描述主轴回转精度理论为基础,利用FFT误差分离方法,从传感器测得的信号中分离并去除检棒的安装偏心及热变形导致的回转中心的偏移量,从而得到精确的主轴回转热误差信息,进而评定数控机床主轴热变形对加工精度的影响。
主轴热变形;复向量;误差分离;回转精度评定
0 引言
机床工作时,在内外热源的作用下,主轴系统的组成部分形成各自的温度场,各组成部分热膨胀性能不一致会导致空间机械结构发生热变形,引起零件的加工误差。受动力学、静力学、热变形以及轴承和轴颈的加工误差等的影响,数控车床主轴瞬时回转轴线在空间位置是不断变化的。实验结果表明:精密车削的圆度误差约有30%~70%是由主轴的回转误差引起的,且机床的精度越高,所占的比例越大[5]。主轴回转精度反映了车床的动态性能,与车床所能达到的加工精度息息相关。车床加工过程中产生的主轴热变形也对主轴回转精度有较大影响,对其进行检测和补偿控制可提高加工精度[6]。随着高速高精机床的广泛应用,检测精度和效率逐渐提高,检测方法从静态检测迅速向动态、在线检测发展。轴系回转误差的测量已从单向测量转向多点测量,测量精度不断提高[7]。
测量主轴回转热误差时,实际的主轴回转轴心是不可见的,只能通过对装卡在主轴上的标准检棒外部轮廓的测量来间接获取主轴轴心的运动轨迹。这样一来,测量结果不可避免地混入了标准检棒的形状误差和安装误差。对于具有高回转精度的精密主轴,混入的形状误差或安装误差有时甚至会淹没掉微小的主轴回转误差,所以对于高精密车床主轴回转误差的测量,混入的形状误差和安装误差不能忽略,必须采取有效的方法从测量信号中分离并去除由测量系统引入的、影响测量精度的信号分量,从而获得主轴回转精度[8-9]。本文以复向量描述的主轴回转精度理论为基础,运用FFT方法对信号进行分解处理,通过分析剔除对主轴回转精度无影响的成分,提取出主轴回转精度,进而评定机床主轴热变形的回转精度并分析其加工精度。
1 主轴热误差测量原理
主轴系统的热变形包括轴向热窜动和径向热变形。测量轴向热窜动时,只需在主轴悬空端安置一个电涡流传感器进行测量即可。主轴径向热变形是二维变量,应采用双向正交法进行间接测量。测量结果包含了主轴制造和安装的误差、热变形等误差,要准确评估主轴热变形对加工精度的影响,需要从综合误差中将热变形误差分离出来。机床主轴回转精度的测量原理是:主轴电机带动主轴做回转运动时产生的径向跳动,使电涡流传感器与被测件表面间的距离发生变化,通过电涡流传感器和信号转换装置将其转换成模拟电压信号,进行定时采集。主轴回转精度对精加工零件的形状精度和表面粗糙度有很大的影响,是评价机床加工精度的重要指标,可预测机床在理想加工条件下所能达到的最小形状误差和粗糙度,也能用于机床加工补偿。
主轴热变形所引起的径向跳动量如图1所示。Oo为理想回转中心,是由主轴支承部件确定的安装中心;Or为主轴实际回转中心;Om为基准球的几何中心;Rm为基准截面的半径;e为检棒的安装偏心量;θ为检棒回转角。电动机运转一段时间后,主轴支承轴承的热变形会导致主轴系统的回转中心Or在不同的温度场下产生偏移,加之运动过程中主轴的随机跳动,使得电涡流位移传感器与被测圆柱表面间的距离发生实时改变,通过电涡流传感器和信号转换器测量得到包含误差信息的位移变化的电压值。

图1 热变形误差信号分析
如图1所示,两个位移传感器检测的位移信号dx和dy分别为
dx=ecosθ+rx(α)+Sx(θ)
(1)
dy=esinθ+ry(α)+Sy(θ)
(2)
式中,ecosθ、esinθ分别为偏心e在X、Y方向上的投影;rx(α)、ry(α)分别为径向运动误差r(α)在X、Y方向上的投影;Sx(θ)、Sy(θ)分别为检棒相差90°的两对应点的形状误差。
测量过程中,采用形状误差远小于回转误差的高精度检棒为基准。在高精度检棒形状误差可忽略的情况下,dx和dy是圆截面中心的位移在X、Y方向的分量。换言之,由于安装偏心的存在,由dx和dy所确定的是圆截面几何中心的轨迹,而不是回转轴心的轨迹。所以,为了尽量减小偏心对dx、dy的影响,使测量结果更能真实地反映r(α),就必须尽量减小或消除偏心量e。
2 误差运动的数学模型
径向运动误差具有周期性和径向性的特征:周期性是指圆轮廓信号具有以2π为周期变化的性质;径向性指圆形横截面的实际轮廓是一个复杂封闭的曲线轮廓,轮廓上各点的径向尺寸有差异,大小不同。被测元件径向回转运动的傅里叶级数描述为
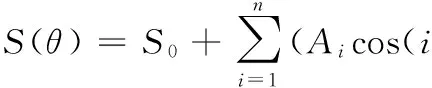
(3)
0°≤θ<360°
式中,n为被测圆轮廓谐波分量的最大谐波阶数;S0为被测圆轮廓数据的直流分量,与传感器初始安装位置有关;Ai、Bi分别为沿X轴和Y轴的i阶次谐波分量的幅值。
式(3)的实际意义是,周期性的径向误差运动可分解成许多个做圆周运动的倍频分量。为了得到真正的径向运动误差,应从测量数据中除去被测元件的直流分量和偏心量e。
3 主轴热误差测量
3.1主轴温度测量
如图2所示,测试对象为FANUC数控车床,分别在主轴电机、前法兰、主轴箱前壁等处布置磁吸式高精度温度传感器,同时采集环境温度的变化。机床在不同转速下空运行,其主轴具体运行情况如表1所示,车床主轴各部件温升曲线如图3所示。各部件温升相异,形成不同的温度场。在室温变化不大的情况下,电机发热温升较快,前法兰亦有较大温升。

(a)温测实验现场(b)数据采集仪图2 机床主轴温度测量

主轴运转速度(r/min)2404809601200主轴运转时间(min)809612670
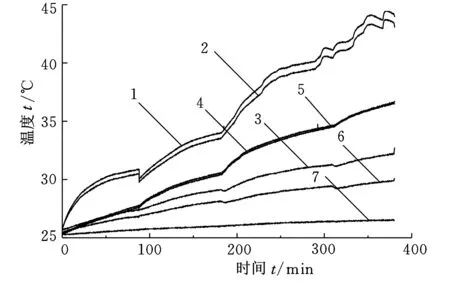
1.电机Y轴负方向 2.电机X轴正方向 3.前法兰X轴正方向4.前法兰Y轴负方向 5.主轴前端壁Y轴负方向6.主轴前端壁Y轴正方向 7.室温图3 机床主轴各部件温升图
3.2主轴径向误差运动检测
如图4所示,采用双向测量法,即两传感器正交分布安装进行检测。检测试验中,用主轴带动检棒的回转来测试主轴的热误差。沿检棒轴向布置2组非接触式电涡流位移传感器(每组2个,共4个)。每组2个位移传感器沿X、Y坐标轴方向上呈正交分布安装,即图4中的S1、S2、S3、S4。主轴的回转误差信号通过这4个位移传感器采集,MX、MY分别为设置在X、Y方向的高速数据采集装置。电涡流位移传感器分辨力为25 nm,数据采集仪的采样频率最高为1 MHz。

图4 双向测量法原理
因测试部位为圆柱孔,不能直接用表检测,故用一根精密检棒插入主轴锥孔内,进行动态测量,如图5所示。

图5 主轴回转误差测量
3.3主轴轴向端面热误差检测
轴向误差是一维误差,故只在检棒端面安装位移传感器进行测量即可。车床主轴的轴向窜动主要影响工件端面的几何形状精度,会产生端面相对于外圆柱面的垂直度误差,但对圆柱工件的外圆轮廓的加工没有影响。主轴的轴向热伸长量随温度场升高而加大,端面跳动量在不同转速、不同温度下呈增加趋势,其相应信号由图4中所示的S5采集。
4 热误差分离及主轴回转精度评定
测量元件的形状误差和安装偏心对主轴回转精度测量结果产生比较大的影响,所以,测量数据中不可避免地混入了形状误差和安装误差,只有有效地分离出形状误差和安装误差,才能对主轴回转精度进行准确评定。径向热变形误差可分解为不同阶次的信号,非接触测量时,测量数据主要由测量检棒的圆度误差信号、截面粗糙度的误差信号和波纹度的误差信号组成,其中,主轴圆度误差属宏观误差,为低频信号;粗糙度误差属微观信号,为高频信号;波纹度误差是介于圆度误差和表面粗糙度之间的中频信号。主轴回转误差中以周期性成分为主,并且主要由1阶、2阶、3阶和4阶的低阶谐波信号组成。因作为基准轴用的试验检棒加工精度高,所以对检棒的圆度误差可忽略不计,且热变形误差分离主要针对径向方向进行处理。
误差分离中,首先应从采集信号S(θ)中除去被测元件的直流分量A0,得到径向运动误差Sn(θ)。Sn(θ)具有周期性和径向性。周期性是指圆周工件轮廓信号的变化是以2π/i为时长、多次重复出现;径向性是指被测件的同一个横截面上的半径在不同位置处各不相同,存在差异性。所以主轴回转时在误差敏感方向上的误差运动可以看成是多个不同倍频的误差信号的叠加。
被测元件敏感方向上的回转运动Sn(θ)的傅里叶级数展开为
(4)
i=1时,S1为测量结果中包含的一阶谐波分量,是与主轴同频的圆周运动信息,由被测元件的安装偏心所致,有
(5)
其初相位θ1为
(6)
i≥2时,Si为每周圈具有i个波峰的内摆线。主轴热误差主要由两部分组成:①主轴支承轴承热变形导致回转中心发生的偏移,在信号中反映为直流分量的变化;②从测量结果中除去被测元件的偏心量就可获得热变形导致的径向运动误差:
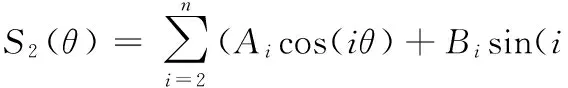
(7)
本文误差信号的频谱分析借助于FFT方法,将时域采集到的离散误差信号变为频域信号,以便分析其误差组成。所以,数据处理时,用傅里叶级数分离检棒的安装偏心量e,也可分离出采样数据中的检棒的形状误差,从而提取出主轴回转误差,流程如图6所示。
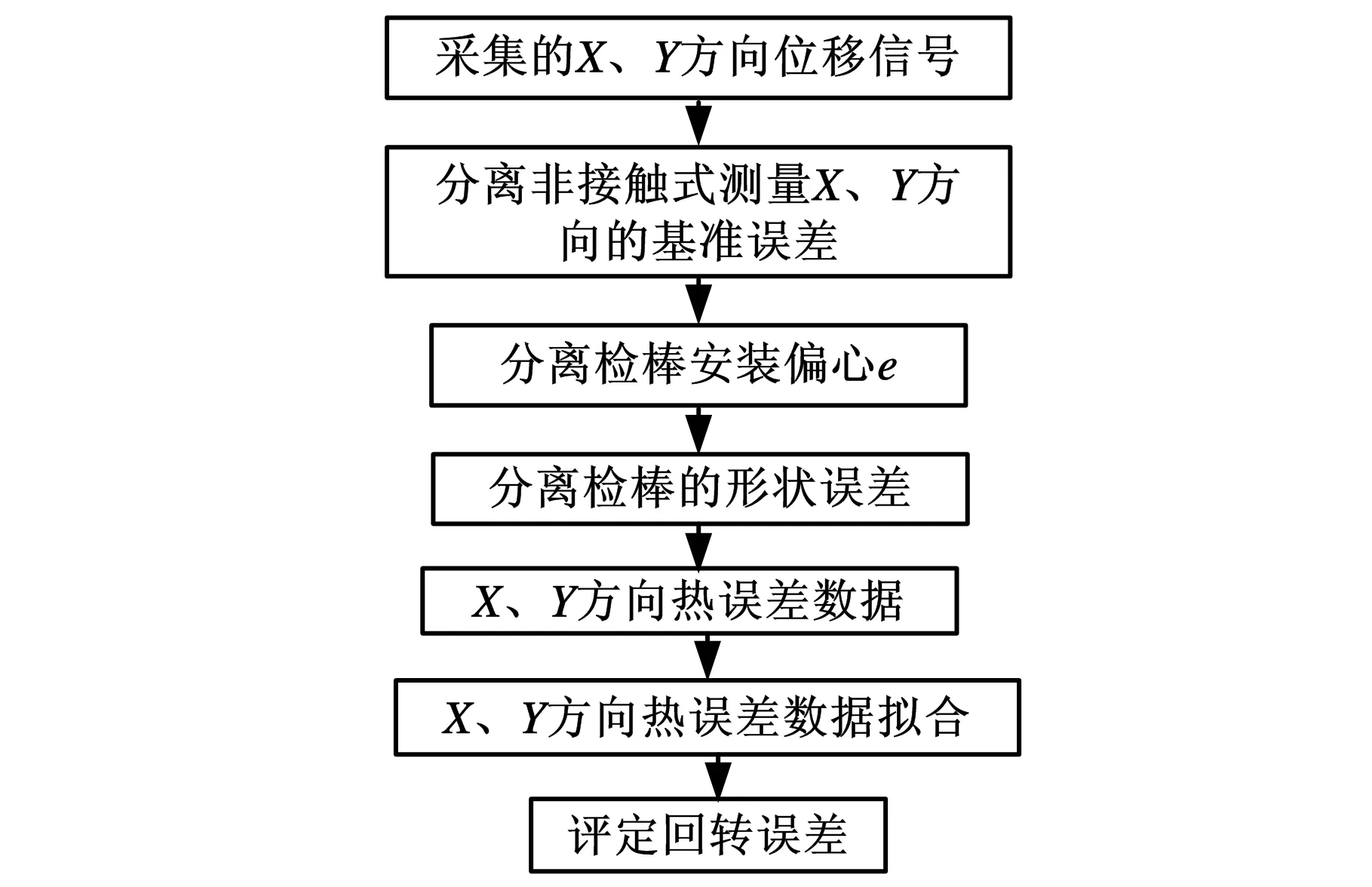
图6 数据处理流程图
图7所示为X、Y方向上的原始数据,其中微小的噪声数据为主轴随机跳动所致。图8为两者的频谱分析图,其中,具有最大幅值的频率接近零,对应着传感器的初始安装位置,其一阶分量为检棒的安装偏心量。图9所示为去除直流分量后X、Y方向的误差测量数据,主要由安装偏心和运动误差组成。图10所示为未分离安装偏心e情况下,在不同时刻(主轴分别以240 r/min,480 r/min,960 r/min速度运行结束时)的径向回转误差的变化情况,尽管有温升的变化,但是偏心量基本不变,均在21 μm左右。图11所示为直流分量分别在240 r/min,480 r/min,960 r/min结束时的情况,它反映了回转中心随温度的变化而发生了偏移。

(a)主轴X向原始数据
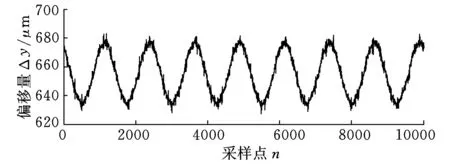
(b)主轴Y向原始数据图7 X、Y方向原始测量数据

(a)X向幅频图

(b)Y向幅频图图8 测量数据频谱分析结果
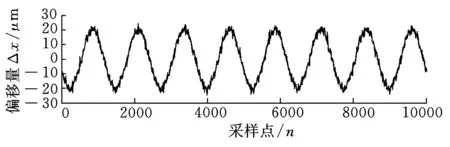
(a)主轴X向原始数据减去直流分量

(b)主轴Y向原始数据减去直流分量图9 去除直流分量后的误差数据

图10 不同时刻的运动误差(未分离安装偏心)

图11 直流分量随温度的变化情况
表2所示为在不同转速、不同的温度场下,基于圆图像法并采用最小二乘圆方法获得的径向热跳动量变化所产生的主轴系统回转精度。如表2所示,随着主轴系统温度的升高,热变形所引起的径向运动误差相应增大。主轴系统的温度上升愈大,其热变形愈严重。
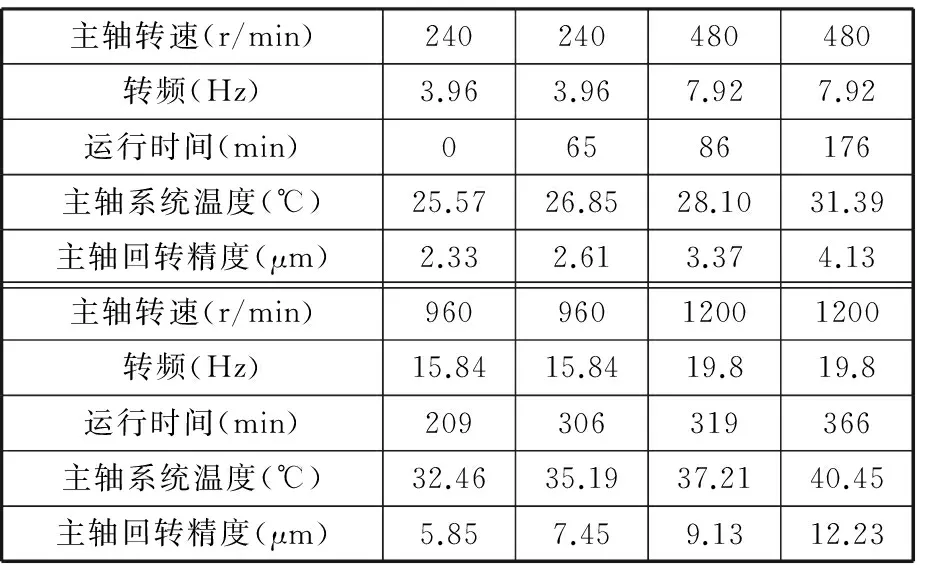
表2 不同转速下的主轴回转误差
5 结论
(1)对测量数据进行FFT谐波分析可知,不同转速下的主轴回转偏心量基本保持不变,其一阶频率与主轴回转频率一致。
(2)主轴在轴向和径向均有热变形,因此,适时地控制机床轴系的温升,可以减小机床主轴的热变形,提高其加工精度。
(3)全面分析了机床主轴回转热误差,由研究结果可以看出,车床主轴在热温升的影响下,其回转误差有加速增大的趋势。通过对实验测量数据
的分析及回转误差评定研究,可以评测机床热变形对主轴回转误差的影响,获得主轴在不同的温度稳定场下,其加工精度的变化状况,为后续机床热变形补偿提供更加可靠的实验依据。
[1]Bryan J.International Status of Thermal Error Research[J].Annals of the CIRP,1990,39(2):645-656.
[2]Weck M,McKeown P.Reduction and Compensation of Thermal Error in Machine Tools[J].Annals of the CIRP,1995,44(2):589-598.
[3]Creighton E,Honegger A,Tulsian A,et al.Analysis of Thermal Errors in a High-speed Micro-milling Spindle[J].International Journal of Machine Tools & Manufacture,2010,50:386-393.
[4]Wanga Yung-Cheng,Kao Ming-Che,Chang Chung-Ping.Investigation on the Spindle Thermal Displacement and Its Compensation of Precision Cutter Grinders[J].Measurement,2011,44:1183-1187.
[5]Yun Won Soo,Kim Soo Kwang,Cho Dong Woo.Thermal Error Analysis for a CNC Lathe Feed Drive System[J].International Journal of Machine Tools and Manufacture,1999,39(7):1087-1101.
[6]Li Yang,Zhao Wanhua.Axial Thermal Error Compensation Method for the Spindle of a Precision Horizontal Machining Center[C]//Proc. 2012 IEEE Int. Conf. on Mechatronics and Automation.Chengdu,2012:2319-2323.
[7]Castro H F F.A Method for Evaluating Spindle Rotation Errors of Machine Tools Using a Laser Interferometer[J].Measurement,2008,41:526-537.
[8]Chen Cha’o-Kuang,Wu San-Ching.A Method for Measuring and Separating Cylindrical and Spindle Errors in Machine Tool Rotational Parts[J].Measurement Science and Technology,1999,10(2):76-83.
[9]Marsha E R,Arnesonb D A,Martinc D L.A Comparison of Reversal and Multiprobe Error Separation[J].Precision Engineering,2010,34:85-91.
(编辑张洋)
Thermal Error Measurement and Rotation Accuracy Evaluation of CNC Lathe Spindle
Li YanLiang LiangLi YinghaoGao Feng
Key Laboratory of NC Machine Tools and Integrated Manufacturing Equipment,Ministry of Education,Xi’an University of Technology,Xi’an,710048
Considering that various types of error components were contained in the thermal errors,the orthogonal method was adopted herein to measure the rotation errors of spindle including radial errors and axial errors resulted from thermal deformation under various temperature fields.Based on complex vector principle of spindle rotation errors,error separation with FFT method was used to separate the eccentric errors of the calibrated artifact and displacement caused by thermal deformation from sampled signals to obtain pure rotation error motion of the rotation axis successfully.So that,the rotation accuracy of spindle concerning thermal deformation was evaluated accurately,its analyzed results provide the experimental basis and reference data for the subsequent thermal error compensation.
thermal deformation of spindle;complex vector;error separation;rotation accuracy evaluation
2014-05-07
国家科技重大专项项目(2012ZXX04012032);陕西省教育厅自然科学计划资助项目(12JK0685)
TH460.40DOI:10.3969/j.issn.1004-132X.2015.12.008
李艳,女,1970年生。西安理工大学机械与精密仪器学院副教授。主要研究方向为数控装备结构设计及检测。发表文章30余篇。梁亮,男,1987年生。西安理工大学机械与精密仪器学院硕士研究生。李英浩,男,1991年生。西安理工大学机械与精密仪器学院硕士研究生。高峰,男,1969年生。西安理工大学机械与精密仪器学院教授、博士研究生导师。

