基于数学本质的概念教学

吴建华

本人曾作为广州市名师应邀在“广州市名师、特级教师教学思想推介研讨会”上执教课例《方程的意义》。

《方程的意义》一课属于概念教学。概念是思维的基本形式，是事物的本质属性在人脑中的反映。数学概念是客观现实中的数量关系和空间关系的本质属性在人脑中的反映。数学概念是一切数学知识和数序思维的基础。在小学数学教学中，引导帮助学生形成正确的数学概念，是数学教学的重要任务。

对于《方程的意义》一课，我们该怎样把握数学本质？在小学数学教材中，方程是这样定义的：含有未知数的等式叫做方程。实质上，方程是为了寻求未知数，在未知数和已知数之间建立起来的等式关系。如此理解，方程的定义是一个发生式定义，刻画的是方程形成或产生的过程。这样的方程本质体现了方程的核心价值，那么在教学中如何基于这一“方程”本质进行教学？

一、概念引入：在已知数与未知数之间建立关系，经历概念发生的过程

方程是含有未知数的等式，是为了解决实际问题，建立已知数和未知数之间的一种等量关系。而让学生学会找等量关系是学生学习方程解决问题的重点和难点。这方面应该贯穿于本单元教学的全过程。本节课是学生初次建立方程的概念，引导学生学会找等量关系是本节课的难点，因此，本课中我从从天平引入，提供了两边可以一起操作的直观模型，引导孩子感悟天平的平衡实质是等式的原型，并在此过程中，引导学生感悟分类的数学思想和方法。

通过观察天平图，得到各式各样的式子，采用自然分类的方法：学生将相关的数学式子写出来后，将它放在相应的位置（等式或不等式）。然后再引导学生观察这些式子的特点，得出方程的定义。在这过程中，分类的标准是在学生已有的学习经验的基础上自然形成的，从而感悟到分类在学习中的作用。

二、概念探究：在构建模型中揭示概念内涵，经历概念形成的过程

2011版小学数学课程标准指出：模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。建立和求解模型的过程包括：从现实生活或具体情境中抽象出数学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果并讨论结果的意义，这些内容的学习有助于学生初步形成模型思想，提高学习数学的兴趣和应用意识。《方程的意义》一课的教学是引导学生感悟模型思想的重要载体。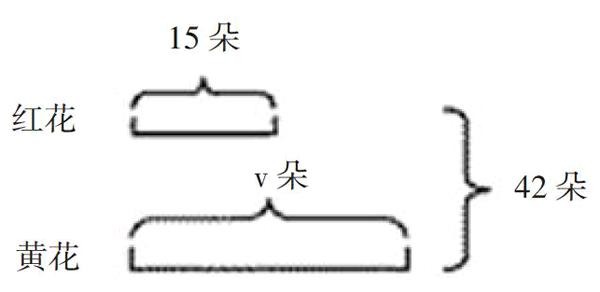

如何更好地使学生感悟模型的思想，促进孩子对“方程”的认识从表征走向本质？我以“天平”为主线，构造模型。

实物天平——各种状态的天平图——平衡状态的天平图——心中的天平——解释方程在生活中的应用。

从实物天平中，引发问题：天平的这种平衡与不平衡的现象和数学有什么联系呢？一下将学生的思维从现实生活中的天平引发到数学思考上来。

提供各种不同状态的天平图，让学生从观察中，用数学的式子表示出天平的状态，从天平的状态抽象出数学问题，然后再用数学的符号建立起等式、不等式，再建立起方程的概念。

平衡状态的天平图：这是学生从“称物体质量相等”的活动转入到“等量关系”的重要一环。怎样引导学生寻找“等量关系”呢？我出具了各种各样的平衡的天平图，如立体图形质量平衡、水果质量平衡……引导学生找到左右两边相等的数量关系，感悟等量关系的建立是列方程的依据。

心中的天平：心中的天平的建立，不是那么容易的事情，它应该在学生读懂题意的基础上建立起来。我以红花和黄花图（如图）切入，找到左右两边相等的数量关系从而建立心中的天平。通过多种图例，引导学生感悟心中的天平既可以是质量相等，也可以是数量相等、路程相等、总价相等……。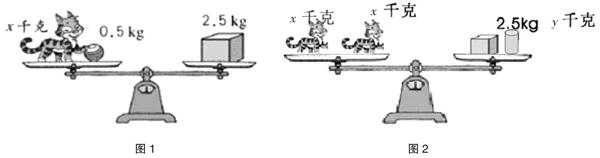

最后，方程在生活中的应用，我设计了一个情景：老师和学生站在一起，有方程吗？当只有师生两个信息时，不存在方程，因为缺了“关系”。然后我提供“三种关系”的信息，让学生选择信息，找到等量关系，从而感受方程就在身边。最后通过讲方程中的“故事”，进一步解释了方程的应用和意义。

三、概念运用：丰富概念的外延，经历数学应用的过程

本课的重点是“理解方程的意义”。我引导学生在“感知方程的多样性”上丰富概念的外延。这“多样性”包括形式上的多样性和数量关系上的多样性两方面。

形式上的“多样性”：引导学生观察小朋友写出的各式各样方程，有含加、减、乘、除法运算的，有一步计算的，两步计算的，有含小括号的，还有的含两个未知数的；在辨一辨、议一议中，感知方程中未知数可以用不同的字母表示，未知数可以参与多种运算……

数量关系表达方式上的“多样性”：因为同样的情境，有不同的数量关系的表达方式，因此用方程表示的形式也不同。

对课堂的练习，我始终坚持立足教材，有效开发，以教材为主、课外习题为辅的原则。教材习题的使用有三种方式：一是有效整合，二是变式应用，三是适当补充。

有效整合：教材习题怎么呈现，怎么整合使用？天平图、各式各样的方程、辨析题、天平平衡图、建立心中天平的相关练习都是教材的原型，怎样有效整合是呈现方式的问题。如观察各式各样的方程中，凸显一些特别形式上的方程；辨析中凸显未知数的多样性等……

变式应用：如本课中，天平平衡图的第二幅图（图2）是课本练习的变式，目的在于引导学生寻找等量关系列出方程，这个方程含两个未知数，分别放在两边，这是一种特殊的方程。对于师生自由创编的环节，也是教材（如图1）的变式。

适当补充：如本课中，我增加了回顾看图写方程的过程，引导学生明确方程的本质意义，增加力度研学课本62页的四幅情境图，目的在于体现怎样处理、用好教材，又如适当补充各种图形图和水果图的天平图，目的在于让学生更好地体会不管天平左右两边放什么、有已知还是未知，只要两边质量相等，都可以写出等式。在认识方程环节，补充“议一议”。在自由创编环节，补充各种关系“老师比学生大28岁，老师和学生的年龄和是48岁，老师的年龄是学生的3.8倍”，补充多种生活中的情景，结合方程“x+5=18”讲故事，目的在于更好地体现方程就在生活中，赋予方程更多的在生活中的应用。

四、教学的核心：数学思想和数学精神的培育

2011版小学数学课程标准把数学学习的总目标定为“四基”——基础知识、基本技能、基本思想、基本活动经验。数学课堂的魅力上，一是体现在教师本身的人格魅力上，二是体现在数学本身的魅力，数学本身的魅力在于其内含的数学思想和数学精神。

在《方程的意义》一课中，不断创设让学生“可触的标高”，引发学生的数学思考。在实物天平中，沟通天平与“数学”的关系；“分类”活动中，不管怎样分，都可以找到同样的式子——“方程”。什么是方程？在平衡的天平图中，可以找到怎样的“等量关系”？如何建立心中的天平？心中的天平可以表示哪些数量相等的关系？光有老师和学生的信息，能找到方程吗？同一情境中，为什么会列出不同的方程？同一方程，怎么表示不同的情境？在这过程中都可以不断渗透“分类”“变与不变”等数学思想。

在数学精神的培育上，从上课伊始的猜谜语中“抓住特征、学会分析”；书写“=”的要求上体现认真、严谨的学习态度；了解方程发展史，体现人类的智慧；感悟方程在数学上的重要地位，在学习“简单”知识中体现的“不简单”；在感知方程的多样性中体验数学学习的乐趣；在自由创编中的“举一反三”……这些无一不是数学精神的教育，而这种教育应该是无痕的，应该贯穿于数学教学的全过程。