对以正态分布法计算医疗器械抽样数量的探索

北京市医疗器械审评中心（100061）张高亮 吴楠 于泳

（接6月下）

整体医疗器械抽样不合格相对率I为各类医疗器械抽样不合格相对率I(i)之和。

对全部医疗器械抽样数量S、各类医疗器械抽样数量S(i)、各类不合格医疗器械抽样数量TN(i)、各类医疗器械抽样不合格率U(i)、各类医疗器械抽样不合格相对率I(i)进行计算，得出医疗器械产品不合格统计见附表2。

附表2 医疗器械产品不合格统计表

2.2.2 医疗器械正态分布概率密度函数对象的选择 各类医疗器械抽样不合格率U(i)主要反映的是各类不合格医疗器械抽样数量TN(i)与全部医疗器械抽样数量S的关系，与各类医疗器械抽样数量无关，在某类医疗器械不合格数量一定，抽样总数量一定的情况下，此类医疗器械抽样不合格率U(i)不会发生变化，但是当此类医疗器械抽样数量变化时，此类医疗器械不合格风险是随之变化的，U(i)无法体现出风险变化，所以不适于使用。

各类医疗器械抽样不合格相对率I(i) 主要反映的是各类不合格医疗器械抽样数量TN(i)与各类医疗器械抽样数量S(i)的关系。在某类医疗器械不合格数量一定，抽样总数量一定的情况下，当此类医疗器械抽样数量变化时，医疗器械抽样不合格相对率I(i)是随风险而变化的，更能体现出医疗器械风险的变化，比各类医疗器械抽样不合格率U(i)更适于使用。

各类医疗器械产品各数值经过计算后，医疗器械产品风险排序对比情况见附表3。

附表3 医疗器械产品风险排序表

通过对比附表3后我们可以发现：卫生材料和其他类医疗器械序号发生变化，其它和卫生材料不合格数量分别为9和7，其它类医疗器械的U(i)大于卫生材料的U(i)；而其它和卫生材料抽样数量分别为118和71，其它类数量大，但是抽样数量同样大，其单位数量下不合格率反而小于卫生材料，说明卫生材料风险更大，因此I(i)排序卫生材料在其它类医疗器械之前。同样，安全套和注射器同为1个不合格，抽样总数量相同，U(i)也相同；而因为各类抽样数量不同，所以I(i)也发生变化。通过对比说明I(i)更有实际意义，选择I(i)建立正态分布概率密度函数更加科学。

故本文选用对各类医疗器械抽样不合格相对率I(i)建立正态分布概率密度函数。

2.3 建立医疗器械产品正态分布概率密度函数 正态分布(Normal distribution)又名高斯分布(Gaussian distribution)，是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。若随机变量X服从一个数学期望为μ、方差为σ^2的高斯分布，记为N(μ，σ^2)。其概率密度函数的正态分布期望值μ决定了其位置，其标准差σ决定了分布的幅度[5]。

我们通过分析可知各类医疗器械产品不合格相对率I(i)服从一个位置参数为μ，尺度参数为σ的概率分布，符合正态分布概率密度函数定义，因此，我们建立各类医疗器械产品不合格相对率正态分布概率密度函数(以下简称正态分布函数)、医疗器械抽样不合格相对率期望值μ、医疗器械抽样不合格相对率标准方差σ。

根据对基础数据进行数学运算，得出各类医疗器械产品抽样不合格相对率I(i)的各类医疗器械抽样不合格相对率期望值μ为0.03396，医疗器械抽样不合格相对率标准方差σ为0.03477。

我们建立医疗器械产品不合格相对率正态分布概率密度函数公式(2-1)，根据正态分布概率密度函数性质，令μ=0，简化后为正态分布概率密度函数(2-2)。

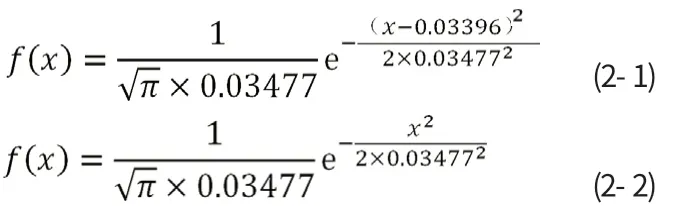
2.4 确定医疗器械产品不合格概率算法 本文通过建立正态分布函数计算医疗器械不合格产品概率的算法主要有两种，对称法和排序法。

2.4.1 对称法计算医疗器械不合格产品概率 基本思路：首先确定医疗器械产品数据正态分布区间范围长度，然后计算各区间内分布概率，最后确定各类医疗器械和概率之间一一对应关系。

（未完待续）