管状填充性椭圆形溶洞的围岩应力弹性解析分析

饶军应，傅鹤林，刘运思，尹泉



管状填充性椭圆形溶洞的围岩应力弹性解析分析

饶军应1, 2，傅鹤林1，刘运思1，尹泉1

(1. 中南大学土木工程学院，湖南长沙，410075；2. 贵州大学土木工程学院，贵州贵阳，550025)

为分析含管状填充性椭圆溶洞的围岩应力，将实际工况简化为计及椭圆孔洞内压()的双向受压无限平面应力问题；以平面弹性复变方法为基础，把平面椭圆外域保角映射到平面圆外域，利用留数定理推导简化力学模型的2个复势函数1()和1()的表达式，得到围岩任意一点应力分量(σ，σ，τ)的解析通式。随后，导出由孔洞内压产生的孔口附加应力场，讨论孔口应力随椭圆形状与围岩侧压系数的变化规律。研究结果表明：产生的附加应力在孔口与轴、轴相交处分别有最大值、最小值；圆形孔洞无内压时，孔口应力的最大值随的增大而减小，最小值与无关。

地下工程；管状填充性岩溶；椭圆孔洞；围岩应力；孔口应力；解析分析

岩溶地质区修建地下工程一直是难点课题，岩溶不仅发育于浅层岩体，而且在地下水位数百米以下的深埋地层仍有大量溶洞存在[1]。地下工程施工揭露的岩溶总是被各类介质充填，高压、富水岩溶隧道开挖过程中，涌水事故时常发生[2−3]。深埋填充性岩溶中的充填介质往往对溶腔壁作用有较大内压，导致溶洞围岩初始应力与无溶洞或有溶洞但无内压时差异显著。为此，学者对含填充性溶洞的地下工程展开了大量相关研究[4−5]，为了从理论上探明溶洞对围岩应力分布的影响，国内外学者普遍把这类问题简化为含孔洞的弹性力学平面问题[6−9]，Howland等[6]基于这种简化并利用平面弹性复变方法，求解了具有单圆孔、双圆孔、单排圆孔和双排圆孔的平面板应力问题，求得孔口的最大、最小应力；陈子荫等[7−9]也采用平面弹性复变方法，对无限平面岩体中具有单个、2个和任意个圆孔的孔口应力进行了解析分析。已有研究表明，将洞室对围岩应力的影响问题简化为带孔洞的无限平面应力问题是可行的，并利用平面弹性复变方法来求解是行之有效的。对地下洞室围岩应力的解析分析，关键是利用保角变换将复杂洞室外域映射到单位圆外域，再将Airy应力函数用2个解析函数1()和1()表示。为解决这一难题，朱大勇等[10]提出超长项级数形式的保角映射函数，并对复杂的非凸型洞室围岩应力进行了解析求解；而祝江鸿[11]把1()和1()中各项积分转换成相应的留数进行求解，并得出了这2个解析函数通式；吴家龙[12]则系统介绍了把平面问题转化为在给定的边界条件下，求解2个解析函数的问题。此外，在解答孔口弹塑性问题时，也可采用复变函数方法来计算平面椭圆孔口塑性区半径，并可用于岩溶隧道 中[13]。但上述研究成果在分析溶洞(或地下洞室)孔口及围岩应力时，均仅把溶洞简化成空腔模型，未考虑溶洞内填充介质对溶腔壁的压力。在分析含填充性溶洞的深埋隧道围岩应力时，由充填介质产生的溶洞内压是不容忽视的，这对深埋岩溶隧道施工安全尤为重要。本文作者以平面弹性复变方法为基础，分析管状填充性椭圆溶洞的围岩及孔口应力情况，力求为预测、防止岩溶隧道开挖时突水、突泥、坍塌等地质灾害提供理论基础。

1 简化模型

1.1 基本假设

为重点考察溶腔及其内压对其围岩应力分布的影响，本文研究基于以下几点假设：

1) 围岩为弹性体，其泊松比为；

2) 溶洞呈管状，其埋深与管状长度均较横截面尺寸大得多；

3) 溶洞横截面形状为椭圆形。

1.2 计算模型简介

基于假设2)，取管状溶洞的某一横截面为研究对象。令椭圆形溶腔的长、短半轴分别为和，其中长轴与水平方向的夹角为，椭圆内区域为，椭圆曲线为，椭圆外区域为，，含填充性溶洞的围岩应力计算模型如图1所示。由于溶洞埋深比其尺寸大得多，故忽略重力梯度影响，简化为双向受压模型；设其上下边界的面力(垂直原岩应力)为，则左右边界面力(水平原岩应力)为，椭圆内边界受均匀压力作用；其中，围岩的侧压系数(1−)，，和均为实常数。

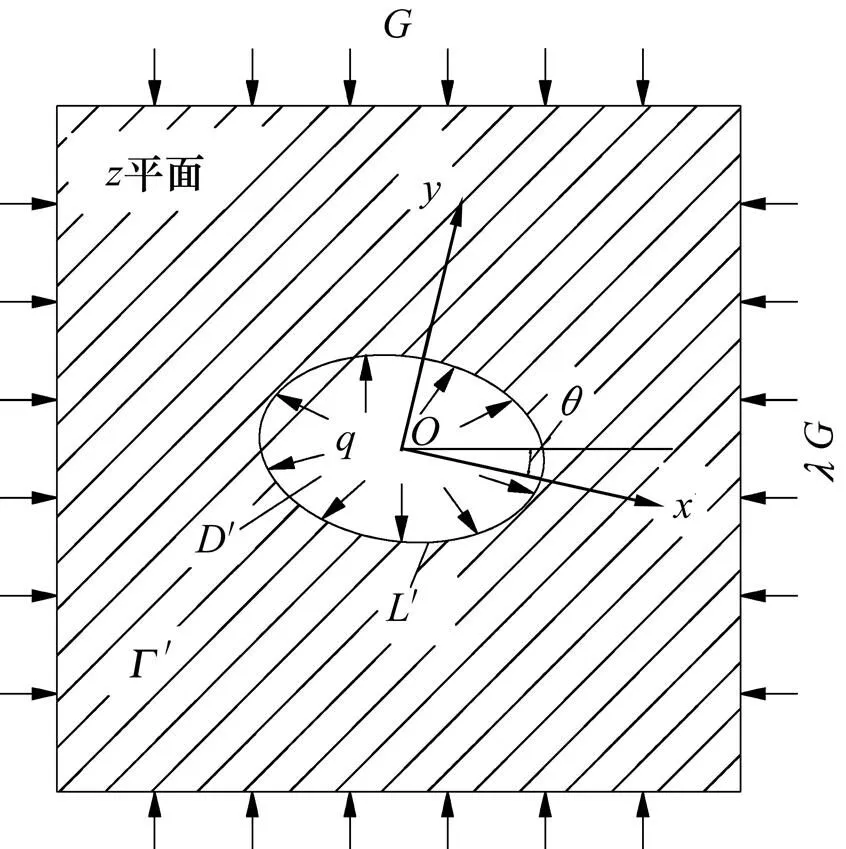
图1 椭圆填充性溶洞的双向受压力学模型

2 平面弹性解析分析一般公式

当溶洞所处埋深比洞径大得多时，可不考虑重力梯度的影响，把重力作用化为无限远处作用有主应力1和2的外载来求解[9]。

现将平面椭圆外域(见图1)保角映射到平面的单位圆外域(如图2所示)，平面的单位圆内域为，单位圆曲线为，单位圆外域为，。其映射可表示为[12]

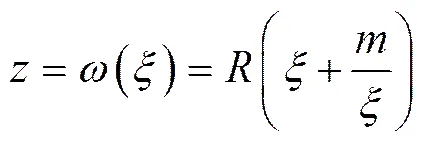
图2 保角映射后平面的力学模型

Fig. 2 Mechanics model from plane to plane with a conformal mapping function

经保角映射后，平面具有单孔的围岩任意一点应力弹性平面解可用平面的复势函数1()和1()表示为[7, 12]

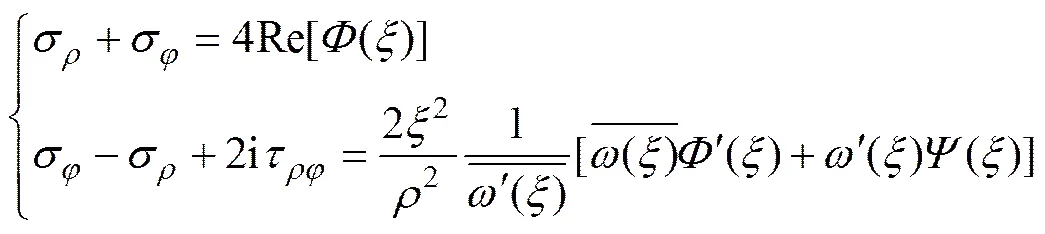
(3)

式(3)中复势函数1()和1()为平面单位圆内的解析函数，可按式(4)对其进行求解。

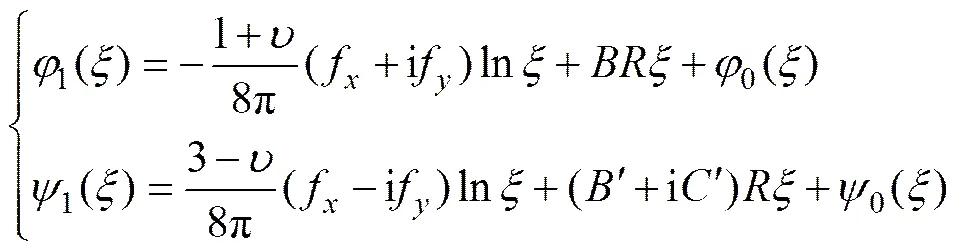
而式(4)中的0()和0()也为平面单位圆外域的解析函数，并可从下式求得：

(5)

式(5)中的为平面在上的取值，可表示为

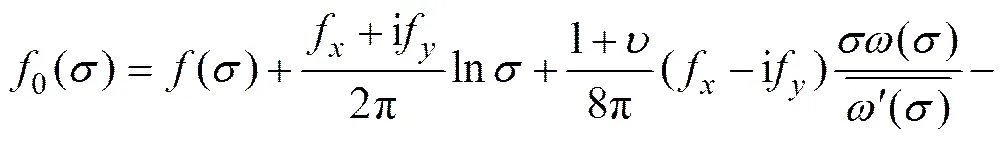
(6)

3 含内压孔无限平面双向受压应力

3.1 复势函数1()和1()求解

若1和2分别为垂直和水平方向的主应力，且主应力2与轴的夹角为，则由边界条件可得：1=−，2=−，再由平衡条件容易得到：

结合式(8)和式(9)，可求得，和如下式所示：

(10)

由图1中边界条件可知：孔洞边界处面力矢量的2个分量可分别表示为

(12)

又因为孔洞内壁所受外力为平衡力系，即整个孔边的面力主矢量。因此，由式(6)有

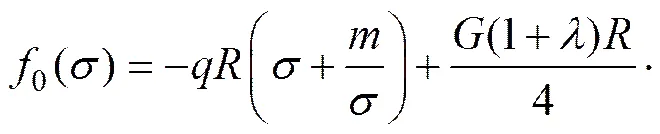
(13)

式(13)中的取值同式(5)中的一致，显然或。因此，可解得如下式所示：

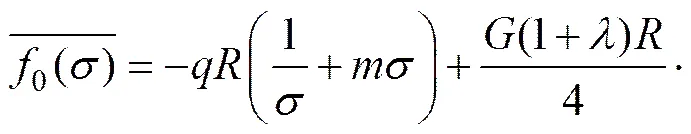
(14)

再将式(13)代入式(5)中第1式便得到0()的表达式为

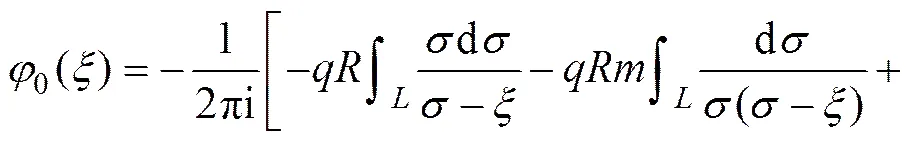
(15)

注意到式(15)存在形如式(16)，(17)和(18)的3个积分待求解：

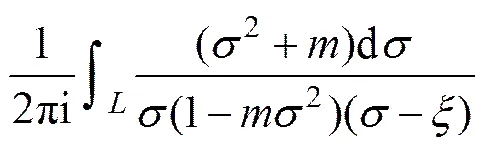
(17)

(18)

由于为单位圆外域任意一点，而1=0为式(16)的一级极点，除该极点外，式(16)的被积函数是圆域内的解析函数的边界值。因此，根据留数定理可求得式(16)为被积函数在一级极点处的留数，即

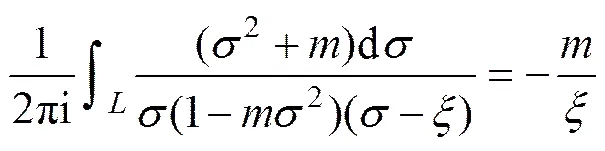
同理，可求得积分式(17)为

(20)

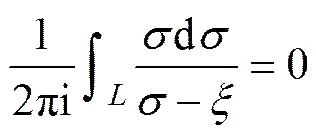
因此，将式(19)，(20)和(21)代入式(15)即可求得0()为

(22)

再由式(22)两边同时对求一阶导数，有

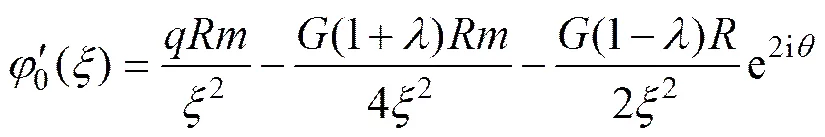
对于0()的求解，将式(14)和(23)代入式(5)中的第2式，发现除含有形如式(17)和(18)两类积分需求解外，还有形如下式的积分待求：

(24)

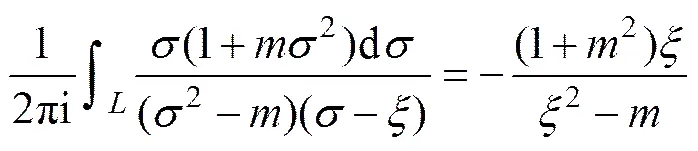
因此，将式(14)和式(23)代入式(5)中的第2式后，结合已求得的式(20)，(21)和(25)的积分值，可解得0()如下式所示：

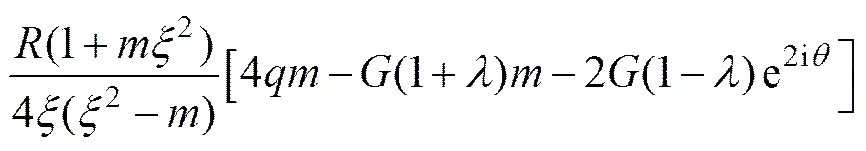
再将式(22)和式(26)分别代入式(4)中的第1式和第2式，整理后有

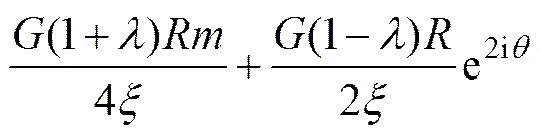
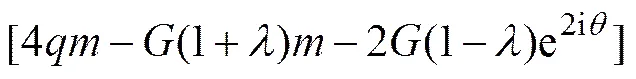
式(27)和式(28)即为含均匀内压椭圆孔围岩应力的复势函数1()和1()的表达式。

3.2 复合函数()和()求解

前文已经解得2个复势函数1()和1()，而由式(2)和(3)可以看出，在求解围岩内任意一点应力分量ρ和φ之前，必须先导出复势函数1()的一阶导数。显然，由式(27)可容易求得其导数为

(29)

对式(1)求一阶导数后，结合式(29)及式(3)中的第一式，便可解得()的具体表达式为

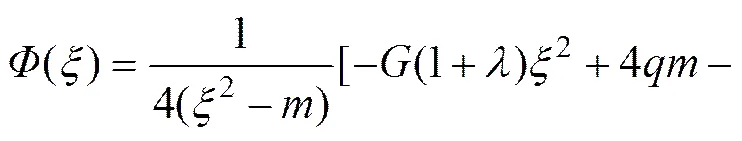
(30)

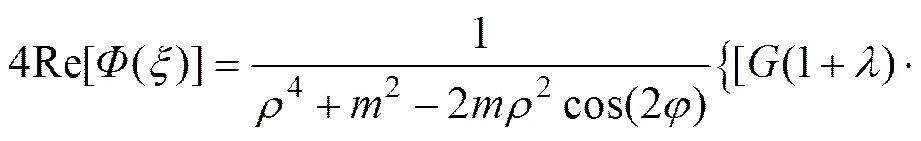
(31)

接下来求解()的表达式。首先，将式(28)两边求一阶导数，可得到：

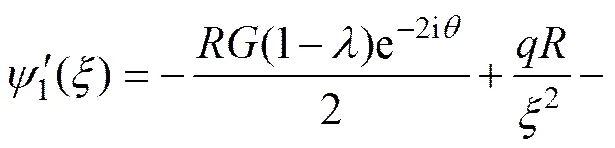
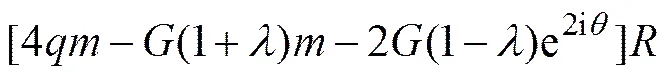
然后，求式(1)的一阶导数后，结合式(32)与式(3)中的第2式，便可得到()的具体表达式为

(33)

式(30)和式(33)即分别为所需求解的复合函数()和()。

3.3 应力分量求解

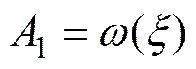
现在把9的实部与虚部分开，令910i11，则由式(34)可知

(35)

最终，从式(35)可求得受双向压缩且含均匀内压椭圆孔洞的围岩内任意一点应力分量为

式(36)即为计及含内压孔洞的双向受压围岩内任意一点3个应力分量的表达式。

4 孔口应力讨论

在溶洞(孔口)边上，有=1且边界条件ρ=−成立。因此，由式(2)的第1式及式(31)可知，孔口的φ将由

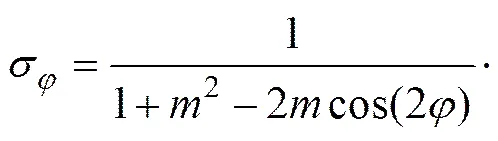
给出，再就式(37)所表示的孔口应力φ展开讨论。

4.1 当=0°时的孔口应力

在=0°时，椭圆溶洞的长轴与轴平行，式(37)可简化为

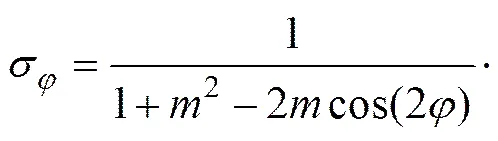
(38)

4.2 当=0时的孔口应力

在=0时，即无穷远处的边界面力不存在，该问题退化为无限平面仅在椭圆孔内壁受均匀压力作用，则式(37)可简化为

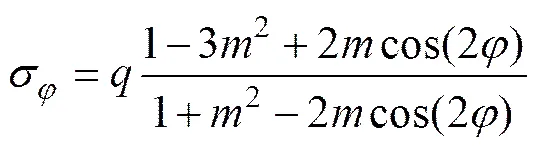
式(39)的物理含义为孔洞内压对孔口的附加应力场，它随和的变化曲线如图3所示。从图3可见：当在[0, π]时，该附加应力曲线存在如下规律。

1) 关于π/2对称，在[0, π/2]随单调递减，而在[π/2, π]随单调递增；

2) 单调递增和递减区间的曲线斜率均随着的增加而增大；

3)在[0, 1]时，附加应力均存在极大值和极小值，各极大值随的增大而增大，各极小值随的增大而减小。

由式(39)也可求得孔口的最大正应力和最小正应力表达式分别为：

: 1—0; 2—0.2; 3—0.4; 4—0.6; 5—0.8; 6—1.0

图3 内压的孔口附加应力随和的变化曲线

Fig. 3 Additional orifice stress changed withandproduced by internal pressure

4.3 当=0°且=0时的孔口应力

在=0°且=0时，即椭圆形溶洞退化为圆形，所需求解的问题退化为在无限平面远边界处双向压缩、圆孔内壁受均匀压力作用的问题。整理式(37)可得

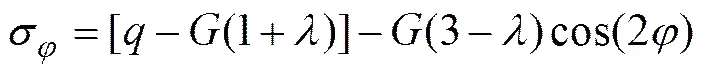
此时，孔口处φ的最大值在±π/2(即椭圆孔与轴相交)处，其最大值为

而φ的最小值在0, π(即椭圆孔与轴相交)处，其最小值为

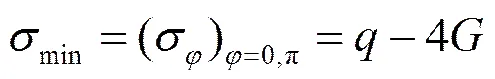
该结果还可用于探讨内压圆孔对周边介质的应力分布影响，如隧道钻爆法施工时炮眼的合理分布研究；也可用于分析深埋圆形洞室开挖，洞壁支护力为时，围岩的应力状态。

4.4 当=0°且=0时的孔口应力

当=0°且=0时，即溶洞为非填充型空腔，不存在内压。经整理后，式(37)可化为

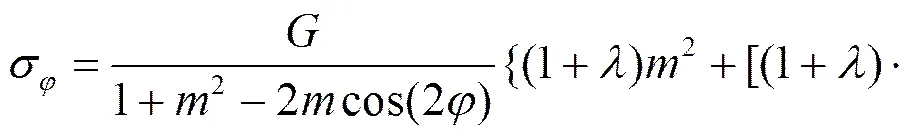
(40)

现对式(40)中的取值进行讨论。

1)=0时，该问题退化为对无限岩体中圆形地下洞室开挖后，暂未施作支护结构的力学模型。此时，式(40)可进一步整理为

式(41)所示为仅受双向压缩时的圆形孔口处的正应力表达式，绘制σ随和的变化曲线如图4所示。当在[0, π]时，这些曲线有如下规律。

①关于π/2对称，在[0, π/2]随单调递增，而在[π/2, π]随单调递减；

②单调递增和递减区间的曲线斜率均随着的增加而减小；

③在[0, 1]时，φ均存在极大值和极小值，各极大值随的增大而减小，各极小值与无关(恒为−4)。

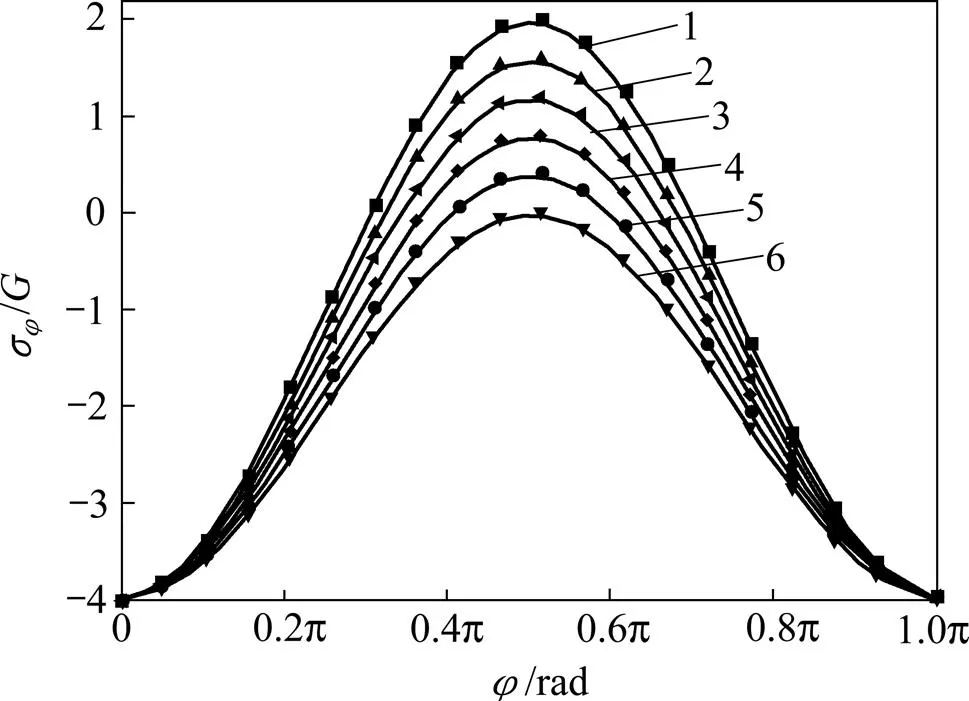
λ: 1—0; 2—0.2; 3—0.4; 4—0.6; 5—0.8; 6—1.0

由式(41)也可求得圆形孔口仅受双向压缩时最大正应力和最小正应力分别为：

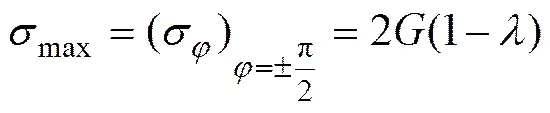
显然，从表达式可以看出：此时最大正应力随侧压系数增加而减小，而最小正应力与侧压系数无关。

2) 当0＜＜1时，则研究对象退化为在无限岩体中椭圆形地下洞室开挖后，暂未施作支护结构的力学模型，在力学上则表示含椭圆孔口的无限平面仅受双向压缩时的孔口应力问题。

由式(40)可得，在椭圆孔与轴相交(即±π/2)处，有

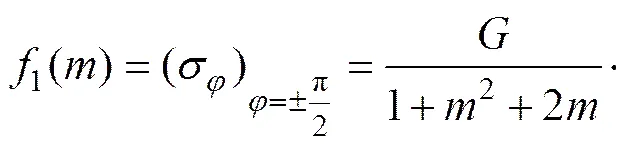
(42)

绘制式(42)所表示的椭圆孔与轴相交处σ随和的变化曲线如图5所示。从图5可以看出：在0＜＜1时：1()随着的增加而减小，=0时1()有最大值，=1时1()有最小值；1()的最大值与最小值分别为

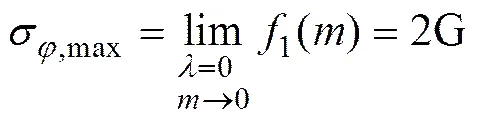
在椭圆孔与轴相交(即0,π)处，有

4.5 当=0且=1时的孔口应力

当=0，且=1(即→0)时，非填充性的椭圆溶洞退化成方向的长度为2的一条贯穿裂纹，同样可以按第3节的步骤求解裂纹两尖端的应力表达式。

5 结论

1) 基于平面弹性复变方法，将含填充性椭圆溶洞的围岩应力问题，简化为求解计及椭圆孔洞内压的双向受压无限平面应力问题；推导了含填充性椭圆溶洞围岩应力的复势函数1()和1()的表达式，并求得了其围岩任意一点应力分量(σ，σ和ρφ)的解析通式；并重点讨论了椭圆孔洞、椭圆孔洞退化为圆形孔洞和孔洞有无内压时的孔口应力情况。

2) 椭圆孔洞的轴比改变时，孔洞内压产生的孔口附加应力的极大值与极小值位置不发生改变，即孔洞与轴的交点处有极大值，与轴的交点处有极小值；该附加应力的极大值随单调递增，而极小值随单调递减。

3) 当椭圆孔洞退化为圆形，且孔洞无内压时，圆形孔口应力的极大值随侧压系数单调递减，而最小值与无关(恒为−4)。

4) 考虑了椭圆孔口的内压对围岩应力的附加影响，更接近于填充性岩溶的实际力学状态；结果可用于探讨内压圆孔对周边介质的应力分布影响，以及分析无限岩体中椭圆形、圆形洞室开挖时围岩的应力状态。

5) 本文仅讨论了单个椭圆形和圆形孔口含内压时的平面弹性应力状态，对其他含内压的任意数量及任意形状的孔口弹性应力或弹塑性应力问题，有待进一步探讨。

参考文献：

[1] 张倬元, 蒋良文. 倒虹吸形成深饱水带大型充填溶洞的典型实例: 圆梁山隧道毛坝向斜深饱水带特大型充填溶洞的形成及充填物成灾机制分析[J]. 工程地质学报, 2010, 18(4): 455−469. ZHANG Zhuoyuan, JIANG Liangwen. A typical case history of infilled karstic caves formed by reverse siphonic circulation in deep phreatic zone: Preliminary analysis of the formation mechanism of infilled huge caves exposed by Yuanliangshan tunneling in deep phreatic zone of Maoba syncline[J]. Journal of Engineering Geology, 2010, 18(4): 455−469.

[2] 莫阳春. 高水压充填型岩溶隧道稳定性研究[D]. 成都: 西南交通大学土木工程学院, 2009: 18−55. MO Yangchun. Stability research on high water pressure filled karst caves tunnel[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2009: 18−55.

[3] 吕建兵, 傅鹤林. 填充性岩溶软基加固方案的模糊综合评价与工程应用[J]. 岩土力学, 2005, 26(增刊1): 244–248. LÜ Jianbing, FU Helin. Fuzzy comprehensive evaluation of reinforcement plan for filling karst soft soil foundation and engineering application[J]. Rock and Soil Mechanics. 2005, 26(z): 244–248.

[4] 刘新荣, 张旭东, 黄明, 等. 深埋隧道填充型溶腔溃水机制及风险识别[J]. 重庆大学学报, 2012, 35(2): 28−34. LIU Xinrong, ZHANG Xudong, HUANG Ming, et al. Feature and risk identification of super karst water burst in deeply buried karst tunnel[J]. Journal of Chongqing University, 2012, 35(2): 28−34.

[5] 吕建兵, 傅鹤林. 隧道填充性岩溶软基弹塑性固结沉降机理研究[J]. 路基工程, 2011(5): 36−39. LÜ Jianbing, FU Helin. Study on the mechanism of elastoplastic consolidation settlement of filling karst soft foundation of tunnel[J]. Subgrade Engineering, 2011(5): 36−39.

[6] Howland R C J, Knight R C. Stress functions for a plate containing groups of circular holes[J]. Philosophical Transactions of the Royal Society A: Mathematical and Physical Sciences, 1939, 238(2): 357−392.

[7] 陈子荫. 围岩力学分析中的解析方法[M]. 北京: 煤炭工业出版社, 1994: 24−89. CHEN Ziyin. Analytic method of mechanical analysis for the surrounding rock[M]. Beijing: Coal Industry Publishing House, 1994: 24−89.

[8] 吕爱钟, 张路青. 地下隧道力学分析中的复变函数方法[M]. 北京: 科学出版社, 2007: 50−74. LÜ Aizhong, ZHANG Luqing. Mechanics analysis with complex variables function in tunnel underground[M]. Beijing: Science Press, 2007: 50−74.

[9] 张路青, 吕爱钟. 双孔圆形洞室围岩应力分析的交替法研究[J]. 岩石力学与工程学报, 1998, 17(5): 534−543. ZHANG Luqing, LÜ Aizhong. Study of alternation method for stress analysis on surrounding rocks of two circular holes[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(5): 534−543.

[10] 朱大勇, 钱七虎, 周早生, 等. 复杂形状洞室映射函数的新解法[J]. 岩石力学与工程学报, 1999, 18(3): 279−282. ZHU Dayong, QIAN Qihu, ZHOU Zaosheng, et al. New method for calculating mapping function of opening with complex shape[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(3): 279−282.

[11] 祝江鸿. 隧洞围岩应力复变函数分析法中的解析函数求解[J]. 应用数学和力学, 2013, 34(4): 345−354. ZHU Jianghong. Analytic functions in stress analysis of the surrounding rock for caverns with the complex variable theory[J]. Applied Mathematics and Mechanics, 2013, 34(4): 345−354.

[12] 吴家龙. 弹性力学[M]. 北京：高等教育出版社, 2001: 174−213. WU Jialong. Elasticity[M]. Beijing: Higher Education Press, 2001: 174−213.

[13] 郭佳奇, 乔春生. 椭圆孔口塑性区及其在岩溶隧道工程中的应用[J]. 铁道学报, 2013, 35(3): 108−114. GUO Jiaqi, QIAO Chunsheng. Plastic zone around elliptical hole portal and its application in karst tunnel[J]. Journal of the China Railway Society, 2013, 35(3): 108−114.

Stress analysis of rocks surrounding a tubular filled elliptical karst cave with complex function of elastic mechanics

RAO Junying1, 2, FU Helin1, LIU Yunsi1, YIN Quan1

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. School of Civil Engineering, Guizhou University, Guiyang 550025, China)

For analyzing the stresses of surrounding rock containing a tubular filled elliptical karst cave, it was simplified to solve the stresses of infinite plane containing an elliptical hole with internal pressure () under bi-axial compressions. According to the complex function of elastic mechanics, the outer region of elliptical hole inplane was mapped to the outer of a unit circle inplane with a conformal mapping function. After that, the complex potential functions of1() and1()were deduced for the simplified model by applying the residue theorem, and the analytic general formula for the component of stresses (σ,σ,τ) were solved. Then, as the elliptical hole was degraded into circular, or the filled karst cave was transformed into unfilled, their stresses were both solved. Moreover, the subsidiary stress field around hole produced by internal pressure was obtained, the variation of opening stress changing with the ellipse shape and the coefficient of horizontal pressure () were discussed. The results show that the subsidiary stress fromgets the maximum value at the point of ellipse intersecting with-axis, while the minimum value is at-axis. As=0 for circular hole, the maximum opening stress is smaller asbecomes greater, but the minimum value has no relationship to.

underground engineering; tubular filled karst cave; elliptical hole; surrounding rock stress; opening stress; analytic analysis

10.11817/j.issn.1672-7207.2015.07.030

U451

A

1672−7207(2015)07−2605−08

2014−07−05；

2014−10−16

国家自然科学基金资助项目(51008308，50878213)；湖南省研究生科研创新项目(CX2013B078) (Projects(51008308, 50878213) supported by the National Natural Science Foundation of China; Project(CX2013B078) supported by the Hunan Provincial Innovation Foundation for Postgraduate)

饶军应，博士，从事隧道、岩土工程等研究；E-mail: rao-ale@163.com

(编辑 杨幼平)