高含水期油藏液流方向优化及流线模拟
李才学,沈曦,贾卫平,毛立华,朱黎明
(1.中国石化中原油田分公司采油六厂,山东 东明 274515;2.中国石化中原油田分公司勘探开发研究院,河南 濮阳 457001;3.中国石化中原油田分公司采油一厂,河南 濮阳 457172)
高含水期油藏液流方向优化及流线模拟
李才学1,沈曦2,贾卫平3,毛立华2,朱黎明2
(1.中国石化中原油田分公司采油六厂,山东东明274515;2.中国石化中原油田分公司勘探开发研究院,河南濮阳457001;3.中国石化中原油田分公司采油一厂,河南濮阳457172)
目前国内大部分油田已经进入高含水开发、剩余油零星分布阶段,造成该现象的主要原因是由于储层平面非均质性、水驱波及程度的不同。为了提高水驱开发效果,需要对液流方向优化进行研究,进一步提高水驱采收率。该次研究以中原油田某高含水油藏为研究对象,将数值模拟和最优理论相结合,建立了基于改进的CRM模型为驱动、EnOpt集合优化为最优化手段,以经济效益为目标函数的液流方向自动化优化方法,从而量化油藏配产配注。以相控精细地质模型为基础,利用流线模拟器进行开发指标预测,确定油井泄流面积、注水井水驱波及面积、水驱速度、井间储层波及面积和井间储层含水等参数。
液流方向优化;流线模拟;配产配注
据统计,目前中国石化大部分油田已经进入了高含水率开发阶段,含水率大于90%的区块地质储量占中国石化整个地质储量的43%,面临递减速度快、稳产难度大的开发难题。高含水油藏剩余油分布零散,下步开采难度大,造成该现象的主要原因是储层平面非均质性、水驱波及程度不同,部分波及程度较低的区域成为剩余油富集区。如何提高油田水驱波及程度,制定配产配注的最优化方案,成为提高油田水驱采收率的主要问题[1-5]。
1 液流方向优化模型建立及求解
新的液流优化模型构架见图1,改进的CRM模型为驱动,EnOpt集合优化为手段,净现值最大为优化方向。优化目标为优化出分阶段的最优注入量、采液量[6-11]。
1.1改进的CRM模型
原CRM模型下,油藏饱和度是常数,无法反映水驱后,含油饱和度变化对传导率的影响。本方法创新之处在于,通过计算各时间步累注与累产数据,不断修正模型各井间传导率。
本质上讲,CRM是一个带有压缩系数的总质量平衡方程。通常,每口生产井同时受效于多个注入井,依据每口生产井周围的控制量,主要的物质平衡可以由不同的方程表示为
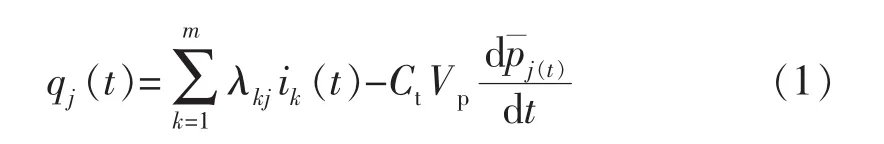
式中:Ct为控制体积周围的总压缩系数,1/MPa;Vp为每口生产井周围的孔隙体积,m3;pj为生产井采出液量的平均压力,MPa;ik为每口注入井的注入速度,m3/d;qj为注入井的总生产速度,m3/d;λkj为注入井与生产井之间的连通系数;t为时间步数。

式中:qkj为注入井k对应的生产井j的产液量,m3。
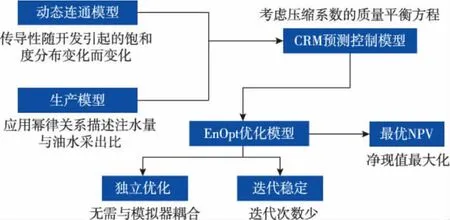
图1 模型流程
依据储层传导性,λkj可解释为

式中:Tkj为注入井k与生产井j之间的有效传导系数。
有效传导系数Tkj是储层表征的一个因素,取值由储层饱和点渗透率决定,因此,在本研究中,规定λkj是一个随时间的变量。式(1)中,生产井总采液量受生产井周围的平均压力和总注入量劈分的注入量决定,但该状态方程在假定注采井间压缩系数很小以及其他井没有流体流动情况下才能成立。为了使方程完全依据流速,引入生产指数模型:

式中:pwf,j为生产井的井底压力,MPa;Jj为生产井的采油指数,t/(MPa·d)。
忽略式(1)和式(4)中平均压力,得到CRM的基本微分方程:
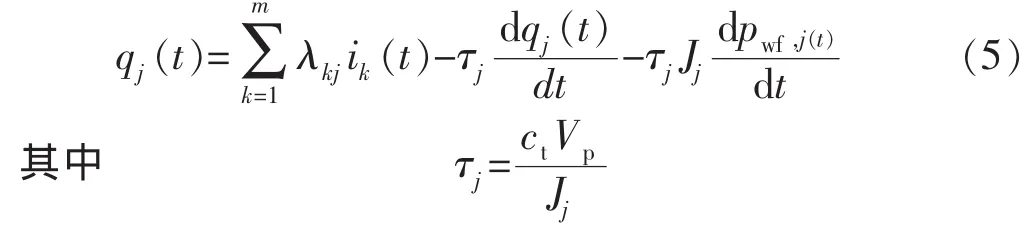
式中:τj为每口生产井驱替体积的时间常数。
同时,为λkj给定了一个m×n的参数,m是τj的参数,n是Jj的参数,可以表述为
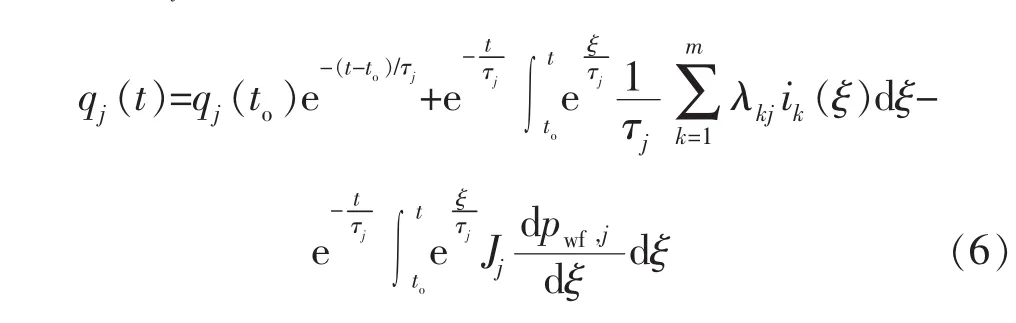
式中:ξ为积分变量,其变化范围为to~t。
1.1.1井间连通性与时间滞留随时间的变化
有关CRM的前期研究都以井间连通性与时间滞留是时间的常数为前提。利用数值模拟方法研究后发现,均质储层中λkj不随注入速度改变而改变。注采井之间有效传导系数Tkj可以根据岩石渗透率、有效剖面、黏度(流体组分黏度之和)、注采井之间的距离、相对渗透率(流体各组分相对黏度之和)等地质参数确定。
解析式(6),假定λkj,Tj,Jj是常数,在本研究中,利用带有分段常数的动力系统模拟了这些参数随时间的可能变化。在这种情况下,式(6)可改写为

在式(7)中,假定τj(tn)和λkj(tn)在每个时间间隔(tn-1,tn)为常数,该解法导致一个时间离散,即在每个时间段,这些参数假定为常数,这可以使CRM的适用性扩展至非成熟油藏,并能提供关于油藏更定量的信息。
1.1.2采油量模型
CRM模型表述了注采井之间总的流体动力情况,在此模型中,不考虑油水之间的区别。不同现象模型可用来描述油井生产情况和液体特征之间的关系。在本研究中,应用了一个幂律关系来描述在第j个生产井(Wj)的累计注水量与油水采出比之间的关系:
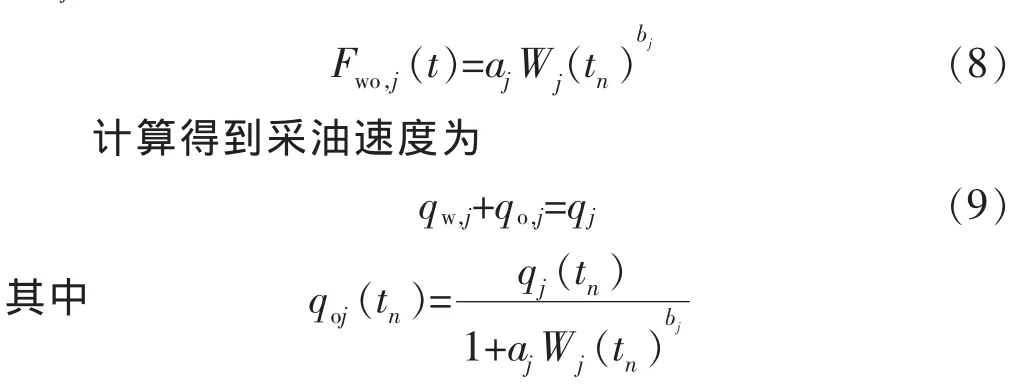
式中:aj为系数。
1.2整体为基础的集合优化(EnOpt模型)
以净现值为目标函数,应用EnKF(卡尔曼滤波)方程进行多参数自动集合最优化逐步迭代,得到最优化的油水井注采量参数。
设y为该系统状态变量。本次研究在每个时间点的y包含:动态参数设置,每口井的总产量qj、每口井的累计注入量Wj、采油速度qo,j;静态参数设置,{λkj},{Tj},{Jj},{aj},{bj},以及可观测的{qj},{qoj}。在EnKF方程中,可观测的参数包含在动态参数之中,但作为可观测的数据,也具分离的特点;因此,观测参数可随系统发展自动更新,但也可通过单次投影所模拟的动力变量得到。状态向量变量的整体被存为Y=(y1,y2,y3,…,yNe)。ENKF程序提供了一个更新状态整体的方法,给出了观测数dobs。
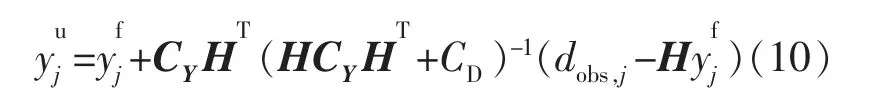
式中:dobs,j为每个整体的扰动观测量;yu为更新的整体;yf为通过数模预测的整体组分状态;CD为测量噪音的协方差;CY为状态向量变量的协方差矩阵;矩阵H为相态向量得到的观测变量。

式中:〈Yf〉为状态向量。
要优化就必须存储一个控制变量的集合,设X为描述控制变量的向量,X=[x1,x2,x3,…,xNx],Nx为控制变量的总数,净现值(NPV)是本次优化的目标函数,由控制向量X和油藏状态向量Y表示。
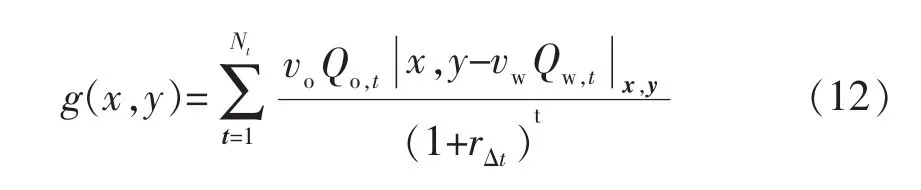
式中:Nt为时间步总数;rΔt为时步Δt基础上的折现率。
为确定年利率,可设定rΔt=exp(rΔt),其中r是年利率,时间步Δt是连续2个控制步之间的时间,控制步相当于可以随时间及时调整的注入速度这一点。例如,总开发时间1000d,就可得到20个控制步,相当于50d为一个时间间隔,这就可以根据优化程序对注入速度进行调整。常数vo和vw分别为原油销售和水处理的单价。Qo,t|x,y与Qw,t|x,y为所有井在控制变量x与状态变量y所表述的t时间点,所有井的累计采油量和产水量。
利用求平均值的方式,在模型的不确定性中优化控制变量。其公式表述如下:
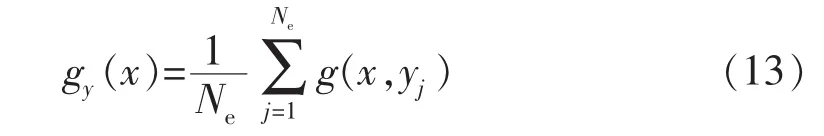
参数y的每个选择都可使目标函数(x,yj)得到不同的值,下标y表示NPV是依据于由EnKF所得的时变模型,模拟状态向量Y在优化部分设为不变量,NPV的优化受控于控制变量x,在每一优化步,更新的控制变量x1由式(14)得到:
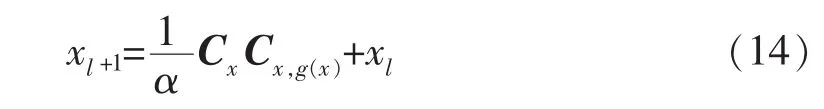
式中:l为优化迭代步;a为决定步长的调优参数;Cx,g(x)为控制变量与g(x)间的互协方差。

式中:xl,j为控制变量摄动值的整体(控制变量是指具有平均值<xl>和前协方差的大小Ne)。
本研究用0平均值作为摄动,对xl进行高斯随机域进行校正。
1.3模拟分析
模拟油田包括5口注入井和4口生产井(见图2)。油田大小:15 m×15 m×2 m,网格数为31×31×5。油水流度比为1,油、水、岩石压缩系数分别为5×10-6,1×10-6,1×10-6,注入井由注入速度控制,其井底压力固定为0.1 MPa。储层孔隙设定为24%,平均渗透率100×10-3μm2。储层存在2个高渗透优势通道:注入井I1与生产井P1之间,优势通道渗透率1 000×10-3μm2;注入井I3与生产井P4之间,其渗透率500×10-3μm2。

图2 概念模型
方案的拟合精度表明,EnKF-CRM的结合可以成功预测CRM在储层研究中的未知参数。作为实际情况来看,EnOpt-CRM程序计算中,目标函数的评价需要单独的数值模拟来计算g(xl+1,yref),当存在真实储层的实际注入速度时,该计算由CRM来执行。
针对不同优化迭代步的注入速度与控制步之间关系的过程中,各个注入速度相关的变化趋势是不同的,注入井I1和I3显示的减低、增加趋势与生产井P2,P4,P5刚好相反,I1和I3相对I2,I4,I5来说,具有更低的注入速度,其优化趋势倾向于改善油藏驱替效率。I1和I3的注入速度低于其他井,这是因为I1-1井组与I3-4井组内更高的渗透率通道造成的。为了得到更高的净现值,靠近高渗透带井的注入速度需要降低,以使整个油藏可以得到更好的驱替。
2 流线模拟技术研究
以相控精细地质模型为基础,利用流线模拟器进行开发指标预测,研究油井泄流面积、注水井水驱波及面积、水驱速度、井间储层波及面积和井间储层含水等参数,开展高含水期油藏的注水利用效率研究[11-14]。
2.1配产配注量优化
应用流线方法描述油水两相驱替过程,要建立油水两相流线数学模型。在黑油模型与流线方法相结合的基础上,尽可能多地考虑地层流体渗流机理。
基本假设:1)忽略气相的存在,流体为油、水两相;2)油藏中流体的渗流是等温的;3)油藏中流体和岩石均不可压缩;4)油藏中流体的流动符合达西渗流定律。
优化流程可以归纳为以下步骤:1)利用流线法对油藏进行数值模拟,并进行历史拟合,重点拟合现场井间受效情况,拟合油水井的连通情况;2)利用流线模拟器,计算每口油井连通的注水井,计算每口注水井注水量平面劈分量,并计算对周围油井产油量的贡献量;3)根据注入水利用率的计算方法计算每口注水井的注水利用率;4)根据注水井的注水利用率分配每口注水井的注水量,同时考虑注水井的注入能力,最大注水量和注水井的最大井底流压;5)按照修改后的配产配注量进行数值模拟,进行下一步优化,返回步骤2)。
2.2理论模型优化
2.2.1流线优化效果模拟
数值模拟的模型使用的是表征河流相沉积的非均质模型,地质模型表征多期河道相互叠置的模型,在平面上沿河道沉积的方法渗透率较高,与河道垂直方向渗透率较低。使用非均值模型在ECLIPSE平台上进行数值模拟,并研究优化方法对提高采收率的效果[15-17]。以五点法进行部署井位,共13口井,其中4口注水井,9口生产井。由于采用的是非均质性储层,井间的连通性差别较大(见图3、图4)。如I2和P5之间的连通性较高,而P3和I2的连通性则较低。
根据水井的注水利用率,I3的注水利用率高,应优先考虑增加I3的注水量,其次是I4的注水利用率;I2的注水利用率在初期就出现了急剧下降的现象,因为I2和P2,P5之间的井间连通程度高,P2和P5很快就见水,含水急剧上升,造成I2和P2,P5之间的无效注水循环。
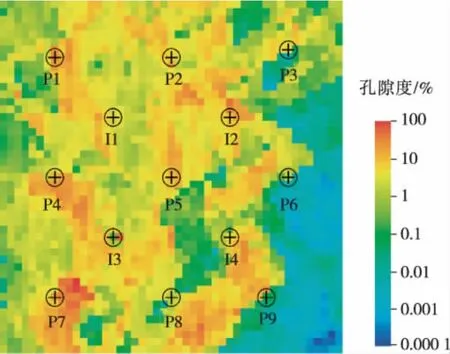
图3 地质模型孔隙度分布
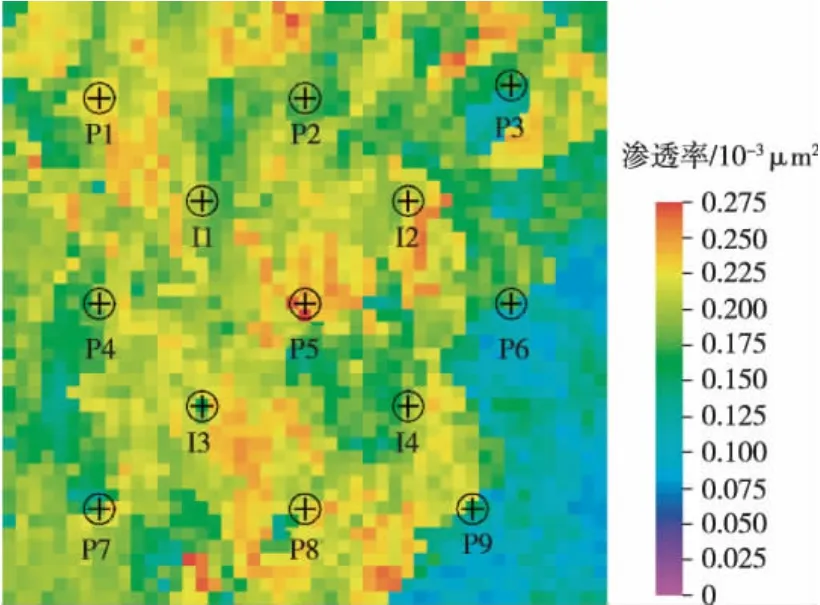
图4 地质模型渗透率分布
对比优化前后的流场,优化前井间存在多个水驱不到或水驱程度低的区域,如井I3和P5,I3和P8,P2和I1中间的储层水驱程度低;而优化之后这些井间的流线较优化前密集,这些区域的剩余油饱和度较优化之前低。优化之后注入水的利用率有了很大的提升,说明注入同样的水,驱动的油量更多,波及体积越大。对比两次模拟结果,优化后的采出程度有了很大的提升,含水也有较大幅度的降低(见图5—8)。
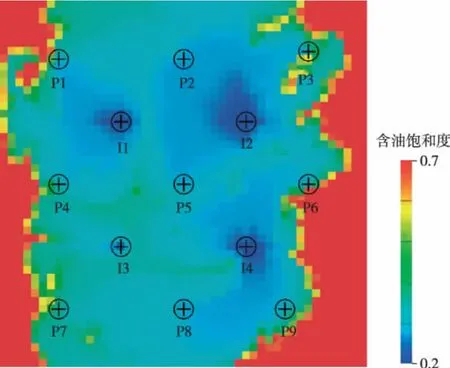
图5 优化前含油饱和度分布
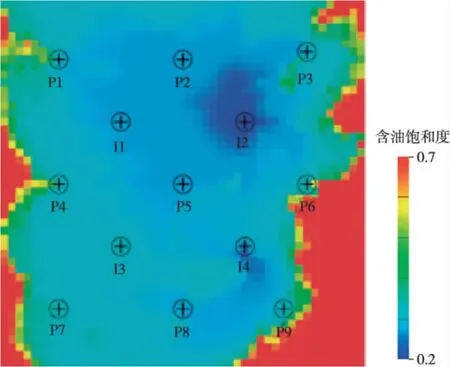
图6 优化后含油饱和度分布
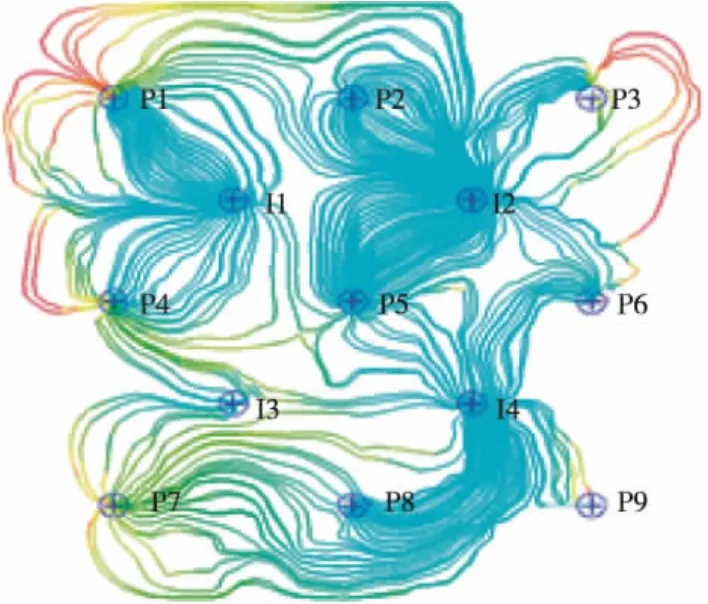
图7 优化前流线

图8 优化后流线
2.2.2优化时机
优化时机对该方法的影响程度也非常明显,进行不同含水阶段的优化效果对比,分别模拟了含水率30%,50%,70%,80%,90%和95%时的方案。对比不同时期的优化效果,进行优化时机的分析(见图9)。
不同含水阶段优化结果对比表明,早期优化的效果最优,优化时间越晚,效果越差;当含水率90%以后再优化效果会剧烈下降。因此,最佳的优化时机是在含水率80%阶段,即使是含水率在95%时进行优化,优化结果对比无优化的方案仍然采收率是提高的。由此可以得出在高含水期进行流线优化仍然能够提高水驱效果。
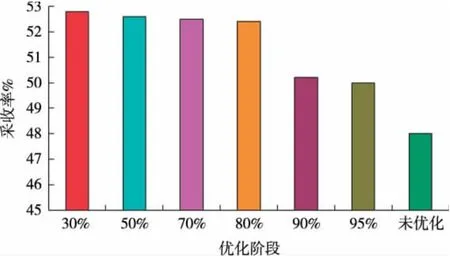
图9 不同时期优化采收率效果
3 矿场应用研究
选择中原油田某区块进行试验区的液流方向优化研究。对目标油藏进行流线模拟评价开发指标,识别高效驱替方向和低效驱替方向;通过液流方向优化方法优化目标油藏单井配注量配产量,进行井组的挑选和液流方向优化矿场应用以及效果分析。
3.1开发历史注采优化
运用该方法,从1990年开始进行优化(见图10)。优化前后整个区块的注入量和产液量完全相同,不同的是每口注水井的注入量,同样每口油井的产液量会有差别,但是为了便于优化前后进行对比,假设整个区块的产液量不变。
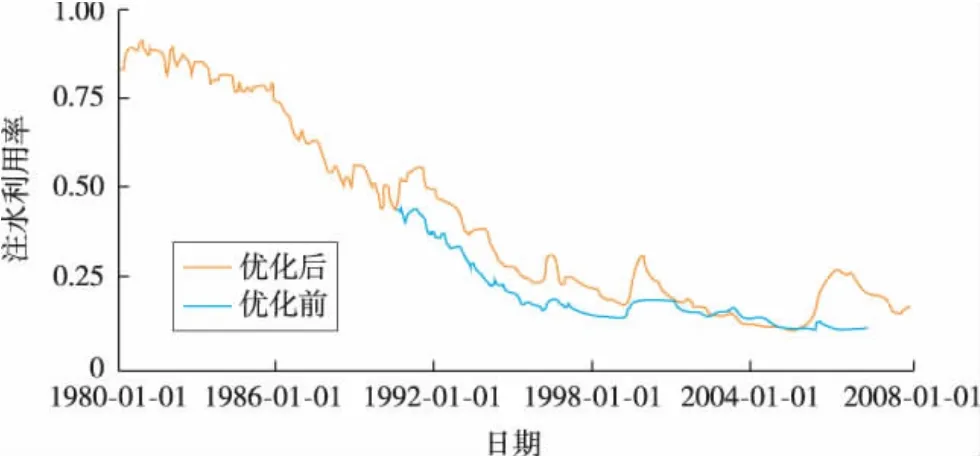
图10 油田注水利用率对比
3.2预测方案优化
储层含水级别统计显示,储层水淹及动用程度较高,储层含水率95%~98%是油层的主体,低含水率储层分布较少,如含水率小于60%的储层只有4%。不同含水率储层注水分配见图11,高含水率储层注水分配程度较高,而低含水率储层的水驱分配程度非常低。如含水率小于90%的储层注入水还不到5%,对于高含水方向,尤其是含水率大于95%的储层,注入水分配程度超过了70%,这些水必然形成无效的水循环,造成油井含水率高,开发效果差。优化后含水率大于98%的储层注入水分配率由33.3%下降到20.9%,而含水率在60%~90%的储层由4.6%上升到15.5%。扩大了对低含水率储层的水洗强度(见图12、图13)。

图11 优化前注入水分布直方图
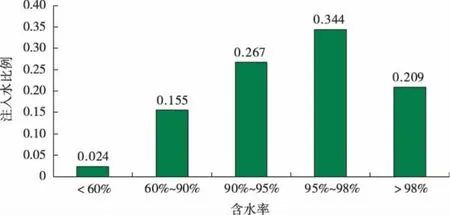
图12 优化后注入水分布直方图

图13 优化前后采出程度
通过流线优化对试验区块进行流线优化模拟。模拟油藏从2013年到2023年的开发动态指标,这期间注入水量427×104m3,优化前累产水396×104m3,累产油22×104t;优化前后的整个区块的注水量相同,优化后累产水394×104m3,累产油24×104t,增油2×104t。
4 结论
1)建立了基于改进的CRM模型为驱动、EnOpt集合优化为最优化手段、以经济效益为目标函数的液流方向自动化优化方法,来求解油藏最优配产配注量,得到每个油水井不同时期的最优注采参数,可以改善油藏驱替效率,提高油藏最终采收率10%以上。
2)根据剩余油的分布规律,建立流线模拟评价模型,对目标油藏进行模拟开发指标研究,可以识别高效驱替方向和低效驱替方向,优化目标油藏单井配注量配产量,实现有效注水,提高开发调整效果。
[1]李东玻.国内外高含水油田特高含水期主要技术措施及启示[J].当代石油石化,2013,26(10):13-15.
[2]王元搏.特高含水期水驱剩余油挖潜技术研究[J].中国石油和化工标准与质量,2011,31(6):160.
[3]王华,邴绍献,张海燕,等.特高含水期水驱油效率计算新方法[J].断块油气田,2013,20(2):201-203.
[4]王德龙,郭平,喻高明.双河油田注采井组剩余油分布规律研究[J].石油天然气学报,2012,34(2):128-130.
[5]邓新颖,殷旭东,尹承棣,等.特高含水期剩余油分析方法[J].断块油气田,2004,11(5):54-57.
[6]俞启泰,谢绪权,罗洪.改变液流方向可行性评价公式[J].断块油气田,2000,7(3):29-32.
[7]计秉玉,杨际平,吕志国.改变液流方向的数值模拟计算[J].大庆石油地质与开发,1994,13(2):73-74.
[8]周书院,陈雷,解立春,等.改变液流方向技术在安塞油田王窑区中高含水期措施挖潜中的应用[J].石油天然气学报,2007,29(3):423-425.
[9]王健,谢华锋.轮南油田中高含水期液流改向数值模拟研究[J].石油地质与工程,2011(3):90-92.
[10]李伟才,崔连训,赵蕊.水动力改变液流方向技术在低渗透油藏中的应用:以新疆宝浪油田北区为例[J].石油与天然气地质,2012,33(5):796-801.
[11]NeliaJafroodi,DongxiaoZhang.Newmethodforreservoir characterization and optimization using CRM-EnOpt approach[J]. Journal of Petroleum Science and Engineering,2011,77:155-171.
[12]张婷.基于流线模拟的井组注采关系定量研究[J].长江大学学报:自然版,2014,11(20):83-86.
[13]罗二辉,胡永乐.流线数值模拟中的流线追踪技术[J].油气井测试,2011,22(3):10-13.
[14]王冰,王焕.流线模拟技术在油藏数值模拟中的应用[J].内蒙古石油化工,2012,(7):80-82.
[15]王敏.泥页岩地层孔隙流体实验数据分析[J].石油实验地质,2013,35(2):199-201.
[16]崔传智,张继庆,杨勇,等.断块油藏典型井组特高含水期配产配注优化研究[J].科学技术与工程,2013,13(3):697-700.
[17]宁士华,肖斐,束宁凯.特高含水开发期曲流河储层构型深化研究及应用[J].断块油气田,2013,20(3):354-358.
(编辑杨会朋)
Fluid flow direction optimization and streamline simulation for high water reservoir
Li Caixue1,Shen Xi2,Jia Weiping3,Mao Lihua2,Zhu Liming2
(1.No.6 Oil Production Plant,Zhongyuan Oilfield Company,SINOPEC,Dongming 274515,China;2.Research Institute of Exploration and Development,Zhongyuan Oilfield Company,SINOPEC,Puyang 457001,China;3.No.1 Oil Production Plant,Zhongyuan Oilfield Company,SINOPEC,Puyang 457172,China)
Because of the planar heterogeneity and different water flooding degree,most oil fields in China have already entered into high water cut development stage,and the residual oil distributes sparsely.In order to optimize the water flooding development,the direction of fluid flow needs to be optimized to improve water drive recovery efficiency.Combining the numerical simulation and optimaltheory,based on improved CRM modeland EnOpt set optimization,taking economic benefit as the objective function,reservoir production and injection proration are quantified in a high water cut reservoir in Zhongyuan Oilfield.Development indexes are predicted by phased fine geological model and streamline simulator.The parameters about product well drainage area,water flooding sweep area of injection well,water flooding speed,inter-wellreservoir sweep area and inter-wellreservoir water are studied.
fluid flow direction optimization;streamline simulation;production and injection proration
TE312.
A
10.6056/dkyqt201505021
2015-03-01;改回日期:2015-07-22。
李才学,男,1968年生,高级工程师,硕士,1990年毕业于成都地质学院石油地质专业,现在从事开发管理与研究工作。E-mail:lclcx001@163.com。
引用格式:李才学,沈曦,贾卫平,等.高含水期油藏液流方向优化及流线模拟[J].断块油气田,2015,22(5):641-646.
Li Caixue,Shen Xi,Jia Weiping,et al.Fluid flow direction optimization and streamline simulation for high water reservoir[J].Fault-Block Oil&Gas Field,2015,22(5):641-646.

