实数的稠密性

张廷桂

（海南师范大学数学与统计学院，海南海口571158）

实数的稠密性

张廷桂

（海南师范大学数学与统计学院，海南海口571158）

实数的稠密性最简单的描述是任意两个不等的实数之间都有无限个其它实数.这个命题的证明是简单的.但是实数的稠密性的另一个含义，即任意两个不等的有理数之间都有无限个无理数，任意两个不等的无理数之间都有无限个有理数，确不容易显式的证明.文章利用实数的十进制表示来详细地证明这个事实.

有理数；无理数；实数

实数是我们从小学到大学数学科目的主要研究对象之一，在大学里的数学分析（微积分）［1-2］、实变函［3-4］等分析类的科目都还需要更深入的了解.我们究竟对实数的了解有多少呢？我们在平日的教学中会说实数与实数轴上的点是一一对应，直观上就是说实数是稠密的，但是我们怎么能够用数学的语言精确地证明这个事实呢？笔者最近从事实变函数论［3］的教学，发现实数的表示是这门课程非常重要的基础内容，而且实数的表示还可以帮助我们证明任意两个不等的有理数之间都有无限个无理数，任意两个不等的无理数之间都有无限个有理数.但是很多教材［3-4］没有详细的涉及这方面的内容，我们本文详细地探讨这一问题.

人类认识数是从自然数N=｛1，2，3，…｝开始，当人们赋予了这个集合N第一个运算法则—加法，发现它对加法是封闭的，即对这个集合内的任意两个元素，进行加法运算，结果仍然在这个集合内.当人类创造了减法运算后，发现这个集合对减法是不封闭，即两个自然数的差不一定还是自然数，这时我们引进了整数Z，当数从自然数集N扩充到整数集Z后，关于加法、减法、乘法运算都是封闭的.但是人们对整数集合进行除法运算时，发现其又是不封闭的，因此数又从整数集扩充到有理数集合有理数集合是对加、减、乘、除（除数不为零）四则运算都是封闭的.有理数有一个重要的性质.

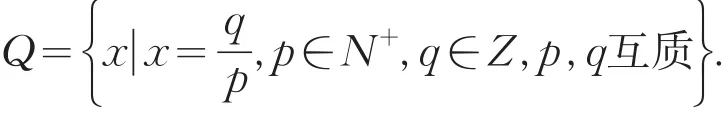
定理1任意两个不相等的有理数之间必有无穷多个其他有理数.

人们把有理数的这种性质叫做有理数的稠密性.以至于在很长一段时间内人们认为有理数就是和实数轴上的点一一对应的.但人们又在研究勾股定理中发现了无理数.用c表示边长为1的正方形的对角线的长度，根据勾股定理知道c2=1+1=2.若c=，其中p，q∈N+，p，q互质，那么2p2=q2由于奇数的平方是奇数，所以q是偶数，设q=2r，r∈N+，又得到p2=2r2，同理p也是偶数，这就与p，q是互质的矛盾.故c不是有理数，这说明了有理数在数轴上还是有空隙的.我们把这些缝隙代表的数叫做无理数，有理数和无理数构成的全体统称实数R.现在直观上看实数是和数轴一一对应的.

那么实数应该也具有一个稠密性的问题，最简单的是任意两个不等的实数之间都有无限个其他实数.这个命题的证明类似于有理数的稠密性，是简单的.但是我们下面证明本文的主要内容，即任意两个不等的有理数之间都有无限个无理数，任意两个不等的无理数之间都有无限个有理数.

为证明这个命题我们需要先介绍实数的十进制表示.

定理2任意实数r∈R，都可以唯一的表示为

其中c0为整数，ci∈｛0，1，2，…，9｝，i=1，2，3，…，n，…，且有无限个ci＜9.证明设c0为满足

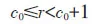
的整数，把长度为1的区间十等分，则存在0，1，2，…，9中的整数c1满足

成立，且当n→∞时，得（1）式成立.

下面证明在所有的cn中必有无限个小于9.事实上，如果存在某个N，使得当n＞N时均有cn=9.则由（1）式有

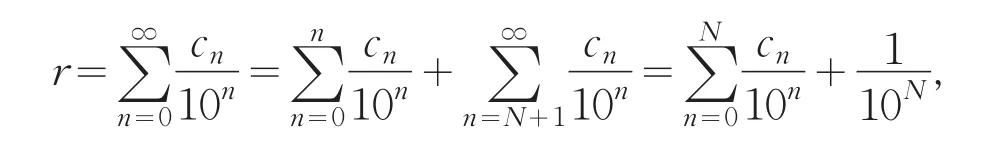
这与（2）式矛盾.故cn中必有无限个小于9.

最后证明唯一性，设r还有另一个不同的表示

假设cn与dn中第一个不等的是第N项，即当0≤n＜N时，cn=dn，当n=N时，cN≠dN，不妨设cN＜dN，由于它们都是整数，所以

由（3）与（4）得

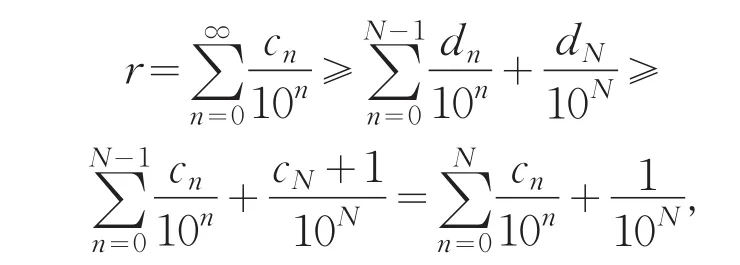
这与（2）式矛盾，唯一性得证.

再利用分数与小数间的关系，我们知道（1）式也可以写成r=c0·c1c2…cn…，其中c0表示整数部分.当它是无限循环小数时表示有理数（有限小数此时看作是以0为循环节的小数），当它是无限不循环小数时，表示无理数.下面我们利用实数的十进制表示，就可以证明我们的主要目标.

定理3任意两个有理数之间都有无限个无理数存在；任意两个无理数之间都有无限个有理数存在.

证明不妨设这两个数是在0到1之间的数.设在实数的十进制表示下两个不等的有理数分别为x= 0·C1C2…Cn…；y=0·E1E2…En….其中Ci，Ei∈｛0，1，2，…，9｝，i=1，2，3，…，且有无限小于9.因为x≠y，不妨设x＜y，再假设｛Ci｝与｛Ei｝序列中第一个不等的元素的下指标是k，即Ck＜Ek，此时我们只需在Ck后面找到第一个不为9的数字Cl，则0·C1C2…Ck…（Cl+1）与0· C1C2…Ek…之间的任意一个无限不循环小数都是我们要找的无理数（就是在（Cl+1）后任意写不循环的0至9的数字）.

同理，设在实数的十进制表示下两个不等的无理数分别为x=0·C1C2…Cn…；y=0·E1E2…En….其中Ci，Ei∈｛0，1，2，…，9｝，i=1，2，3，…，且有无限小于9.因为x≠y，不妨设x＜y，再假设｛Ci｝与｛Ei｝序列中第一个不等的元素的下指标是k，即Ck＜Ek，此时有限小数0·C1C2…Ek，0·C1C2…EkEk+1，……等就是我们要找的有理数.

文章主要应用实数的表示理论讨论了实数的稠密性，精确地证明了一个看似简单的事实：任意两个有理数之间都有无限个无理数存在；任意两个无理数之间都有无限个有理数存在.

［1］华东师范大学数学系.数学分析（上）［M］.3版.北京：高等教育出版社，2001.

［2］曾广洪，张晓霞，吴庆初.微积分［M］.北京：高等教育出版社，2014.

［3］程其襄，张奠宙，魏国强，等.实变函数与泛函分析基础［M］. 3版.北京：高等教育出版社，2010.

［4］王昆杨.实变函数讲义［M］.北京：高等教育出版社，2011.

责任编辑：刘红

The Denseness of Real Numbers

ZHANG Tinggui
（College of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China）

A simplest description for the denseness of real numbers is that there are an infinite real numbers between any two real numbers.In this paper，we demonstrate the fact there are infinite irrational numbers between two unequal arbitrary ra⁃tional numbers；between any two irrational number there are infinite numbers of rational number.

rational number；irrational number；real number

O 174.11

A

1674-4942（2015）04-0372-03

2015-09-13

国家自然科学基金（11501153）