关于M-矩阵最小特征值的几个不等式
李艳艳
(文山学院 数学学院,云南 文山 663099)
关于M-矩阵最小特征值的几个不等式
李艳艳
(文山学院 数学学院,云南 文山 663099)
首先给出了不可约M-矩阵最小特征值q(A)界的较易计算的新不等式,其次利用该不等式与柯西-施瓦兹不等式,得到了M-矩阵AC-1的最小特征值q(AC-1)的新的不等式。这些结果是对M-矩阵最小特征值界的估计的有益补充。
M-矩阵;Hadamard积;最小特征值;不等式
1 预备知识
记Cn×n(Rn×n) 表示n×n阶复(实)矩阵集,N= { 1, 2, …, n} 表示自然数集。
设A = (aij)∈Rn×n,1)若aij≥ 0,则称A为非负矩阵(A≥ 0);2)若aij≤ 0,i≠j,则称A为Z矩阵;3)若A为Z矩阵, 且A-1≥ 0(A-1为A的逆矩阵),就称A为非奇异M-矩阵。
矩阵A = (aij),B = (bij)∈Rn×n的Hadamard积为AB = (aijbij)∈Rn×n,矩阵A的r次Hadamard幂为A(r)=为正整数)。
令q(A)=min{ Re(λ), λ:∈σ (A)} ,σ (A)是Z矩阵A的特征值的集合。
M矩阵A = (aij)分裂为A = DA- CA(DA= diag(a11, a22, …, ann),称JA= DA-1CA为A的迭代矩阵。
M矩阵C = (cij)∈Rn×n的逆矩阵C-1= ( βij)∈Rn×n≥0,分裂为C-1= EC-1- FC-1,EC-1= diag( β11, β22, …,βnn),称的迭代矩阵。
引理1[1]设a=(a1, a2, …, an)T≥ 0 ,b=(b1, b2, …, bn)T≥ 0 ,则有
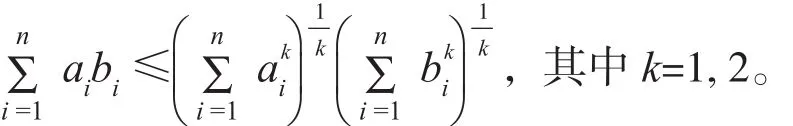
引理2[2]设A是不可约M-矩阵,则
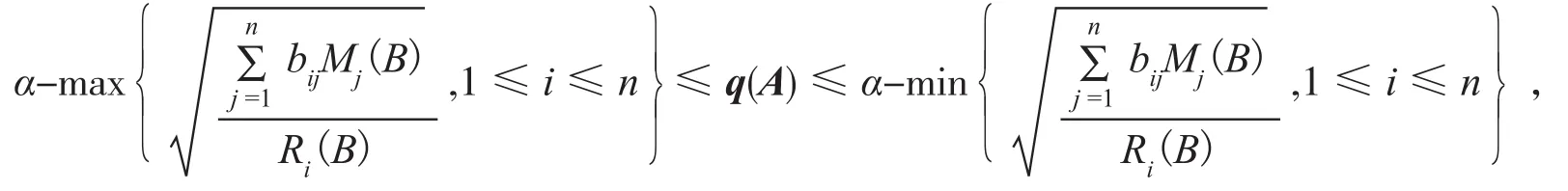
2 主要结果
定理1 设A是不可约M-矩阵,则

将以上两方面应用到引理2得

定理2 设A = (aij)∈Rn×n,C = ( cij)∈Rn×n是M-矩阵,则C-1= ( βij)∈Rn×n≥0,且
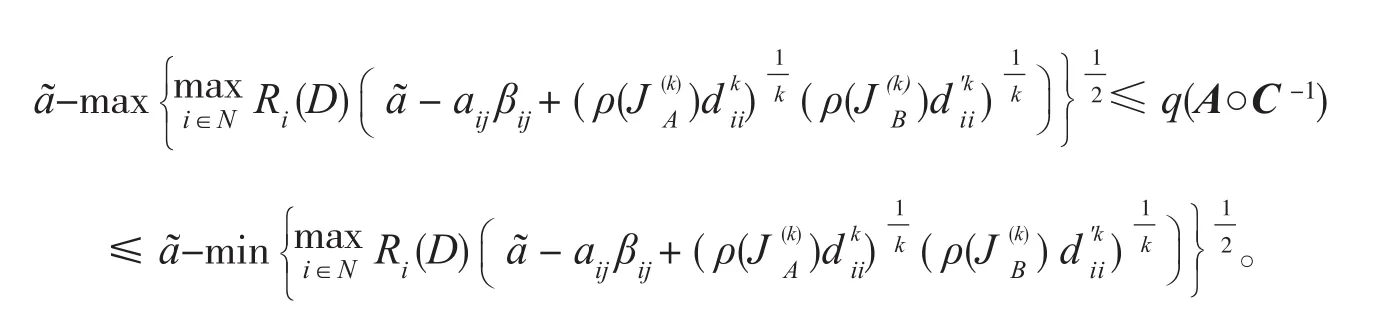
证明
设U = diag (u1, u2, …, un),V = diag (v1, v2, …, vn),ui, vi> 0
W = UV = diag (u1v1, u2v2, …, unvn),则


3 数值算例
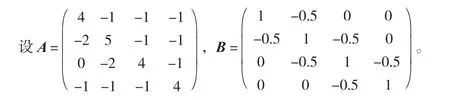
[1] 杜琨.矩阵Hadamard积和Fan积的特征值的界[J].华东师范大学学报,2008(5):45-50.
[2] 章伟,黄廷祝.不可约M-矩阵最小特征值的估计[J].工程数学学报,2004(6):31-34.
Some Inequalities on the Minimum Eigenvalue of M- matrix
LI Yanyan
(School of Mathematics, Wenshan University, Wenshan Yunnan 663099, China)
First of all, more easily calculation new inequality of irreducible M- matrix of minimum eigenvalue are given. Next the new inequalities of minimum eigenvalue of M- matrix is obtained through the inequality and cauchy-schwarz inequality. These results are benefi cial to the estimate of the M- matrix minimum eigenvalue bound.
M- matrix; Hadamard product; minimum eigenvalue; inequalities
O151.21
A
1674 - 9200(2015)06 - 0059 - 04
(责任编辑 刘常福)
2015 - 03 - 19
云南省教育厅科研基金项目“几类对角占优矩阵的逆矩范数界的估计”(2013Y585);文山学院重点学科“数学”建设项目。
李艳艳,文山学院数学学院讲师,硕士。

