基于尺规作图的新型公切线画法

张菁宇　李虎祥

摘要：简述了公切线的定义、性质，介绍了新型公切线尺规作图方法，并对这种尺规作图法进行了数学原理论证。

关键词：公切线；尺规作图；数学原理

引言

在生活工作中，公切线被广泛运用在各个领域。在生活中，自行车链轮传动中的运用；在工作中，拖拉机发动机之间带轮传动的运用等等，公切线在机械设计制造中被运用到的例子层出不穷，公切线给人类带来了广泛的好处、方便、美观。为了更好地将公切线运用在为人类服务行业中，我们在机械设计制图工作中，会了解公切线，会运用公切线变成了一种实际需要，下面就介绍一种新型尺规作公切线的方法及其数学原理论证。

1.公切线

和两个圆相切的直线叫作这两个圆的公切线。公切线有两种，如果两个圆在公切线的同侧，则这公切线叫外公切线；如果两个圆在公切线的异侧，则叫内公切线。如图1、图2所示。

2.公切线尺规作法

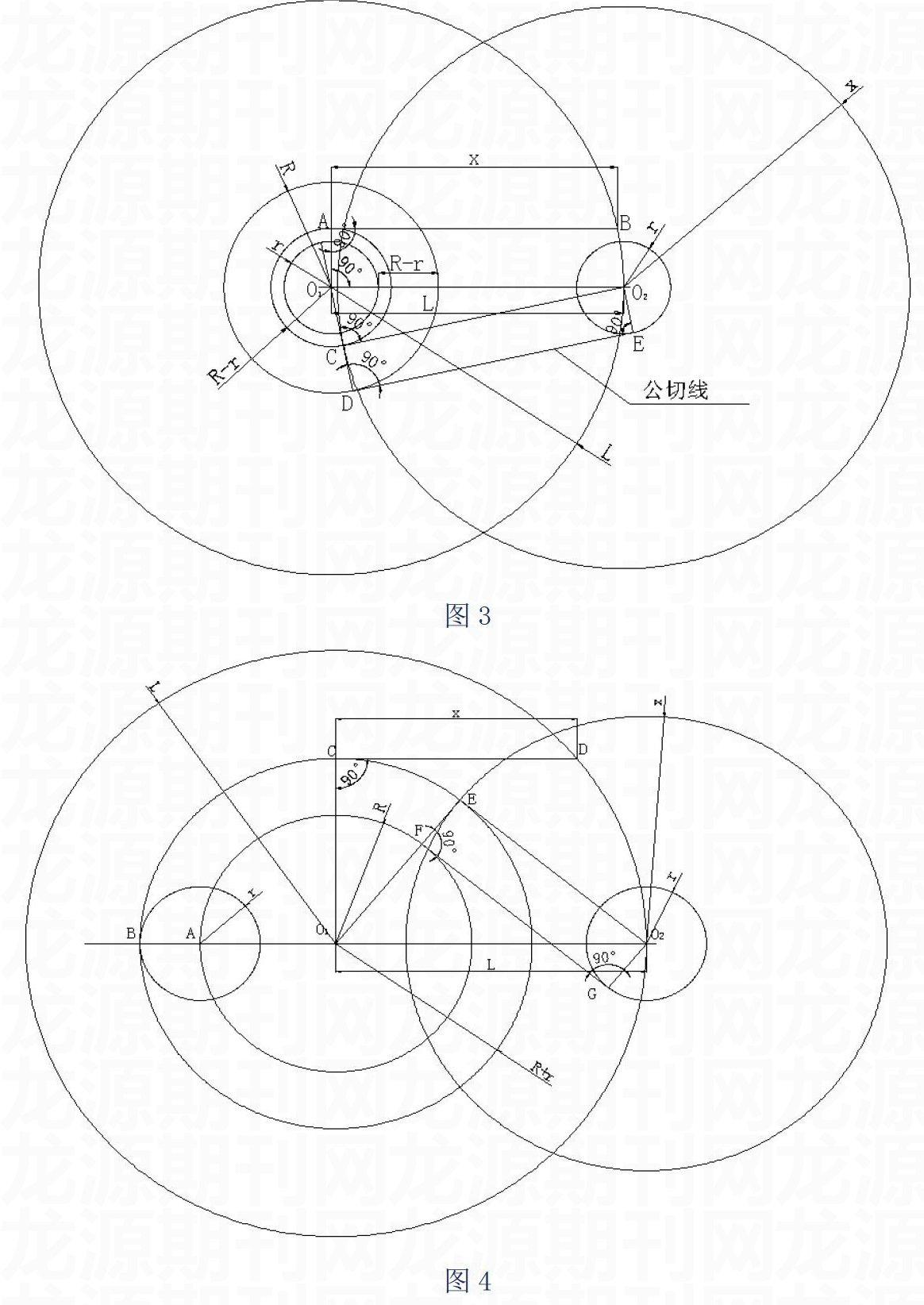
2.1 外公切线尺规作法

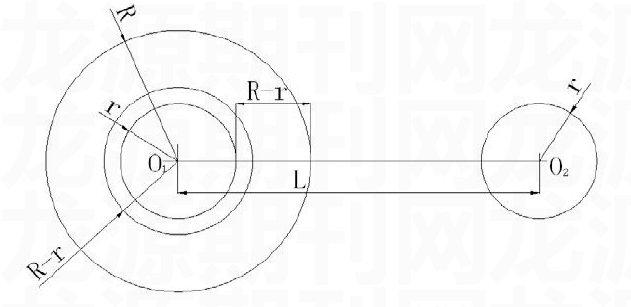
第一步：作大圆O1、小圆O2，其中圆O1的半径为R，圆O2的半径为r、两圆圆心O1O2间距长度为L（其中：L>R+r>R>r>0）。过圆心O1作一半径为r的圆r。

第二步：定义线段O1O2上一线段长度为R-r，如上图示。

第三步：过圆心O1作一半径为R-r的圆R-r。

第四步：过圆心O1作一半径为L的圆L；过圆心O1作线段O1O2的垂线O1A，点A为与圆R-r的交点；过A点作线段O1 A的垂线AB，点B为与圆L的交点；定义线段AB长度为x。

第五步：过圆心O2作一半径为x的圆x，与圆R-r的交点为C，连接圆心O1与点C；延长O1C与圆R相交于点D；连接圆心O2与点C，得一线段O2 C。

第六步：过点D作O1D的垂线DE，过圆心O2作直线DE的垂线，交点为E，则直线DE即为所求公切线。（以下为外公切线数学原理证明。）

2.2 内公切线尺规作法

第一步：作大圓O1、小圆O2，其中圆O1的半径为R，圆O2的半径为r、两圆圆心O1O2间距长度为L（其中：L>R+r>R>r>0）。

第二步：延长直线O1O2交大圆O1于点A ；过点A作一半径为r的圆r，交直线O1O2于点B。过圆心O1作一半径为R+r的圆R+r。

第三步：过圆心O1作一半径为L的圆L；作直线O1O2 垂线段O1C，交圆R+r于点C，过点C作线段O1C的垂线段CD，交圆L于点D，定义线段CD长度为x；过圆心O2作一半径为x的圆x，交圆R+r于点E。

第四步：连接圆心O1与点E，交圆R于点F；连接圆心O2与点E。

第五步：过点F作直线O1 E的垂线FG，过圆心O2 作直线FG的垂线段O2G，交点为点G。则直线FG即为所求公切线。（以下为内公切线的数学原理证明。）

3.结束语

尺规作图法作公切线是一种简便的机械制图方法，在教学中能得到广泛的应用，在工程中也不愧是一种简便的作图方法，因此有必要加以推广。