基于MATLAB的桥式起重机点动工况系统响应研究

晋跃　徐凯

摘 要：对桥式起重机进行简化建模，求出受单冲量及间断冲量条件下系统响应函数，进而找出系统结构阻尼系数对点动冲量所引起主梁振动周期以及振幅的影响关系。借助高精度的数值分析及数据可视化建模仿真软件MATLAB绘制函数曲线，避免了传统非交互式程序设计语言繁琐的编辑处理模式，有效地缩短起重机主梁疲劳寿命及振动响应的优化设计周期并提高了设计质量。

关键词：桥式起重机；冲量；系统响应

引言

对提升载荷的起重机而言，从货物离地的匀加速起升阶段到货物匀速起升阶段，主梁所受到的振动远不及冲量所带来的影响，尤其是受到间断冲量作用的工况，主梁受到不等交变应力幅的振动响应，如此的交变应力极易使主梁结构产生疲劳裂纹，而盲目地通过选用优质材料而提高疲劳强度或加大系统运动刚度势必会带来不必要的材料浪费或降低整机系统的工作效率[1，2]。起重机的点动工况是一种使用频率极高的工况，主梁所受载荷为冲击载荷，因而通过研究系统阻尼与该工况下系统响应的关系，在满足功能性要求的前提下，对指导起重机系统主梁结构的优化设计、提高系统疲劳寿命并满足其经济性要求[3]显得尤为重要。

1.简化建模

桥式起重机一般由桥架、起升机构、大/小车运行机构、小车导电装置等组成，为了实际研究需要，将电动单梁起重机进行科学地简化建模如图1（a）所示，将主梁简化为一具有阻尼和刚度的构件，等效质量利用动能原理求解出，电动葫芦简化为一具有重量的质量块连接于主梁上，忽略承重后的钢丝绳阻尼作用，将其视为弹性构件。将图1（a）中的质量及刚度系数进一步等效为图1（b）所示的单自由度振动系统，其中 为系统等效刚度， 为系统等效质量， 为阻尼系数，可通过计算或实验的方法确定。

2.响应函数建立

引入阻尼比 ，无阻尼系统振动频率 ，其c为系统阻尼系数， 为临界阻尼系数， 为系统等效刚度， 为系统等效质量

得到阻尼系统自由振动响应通解形式：

本文重点研究电动单梁起重机，针对欠阻尼系统响应：

振动系统初始条件： 和 ，阻尼系统振动频率 ，将系数b的兩复数形式 带入式3.4得到系统响应：

3.MATLAB求解及仿真分析

以电动单梁起重机为例，参数如下：主梁质量 ，主梁有效跨度L=19.5（m），电动葫芦质量 ，起升重物质量取 ，所受冲量 ，钢丝绳有效长度 ，钢丝绳直径 ，主梁及钢丝绳杨氏模量 ，主梁惯性矩近似取 ，其中B，H，b，h为截面腔体的宽、高，系统阻尼系数取 ，考虑冲量加载对主梁影响较大的工况即小车位于跨中起升钢丝绳长度为8米。

则系统等效刚度

其中 为主梁有效刚度， 为钢丝绳有效刚度

当起升重物位于梁的跨中，由梁的动能关系：

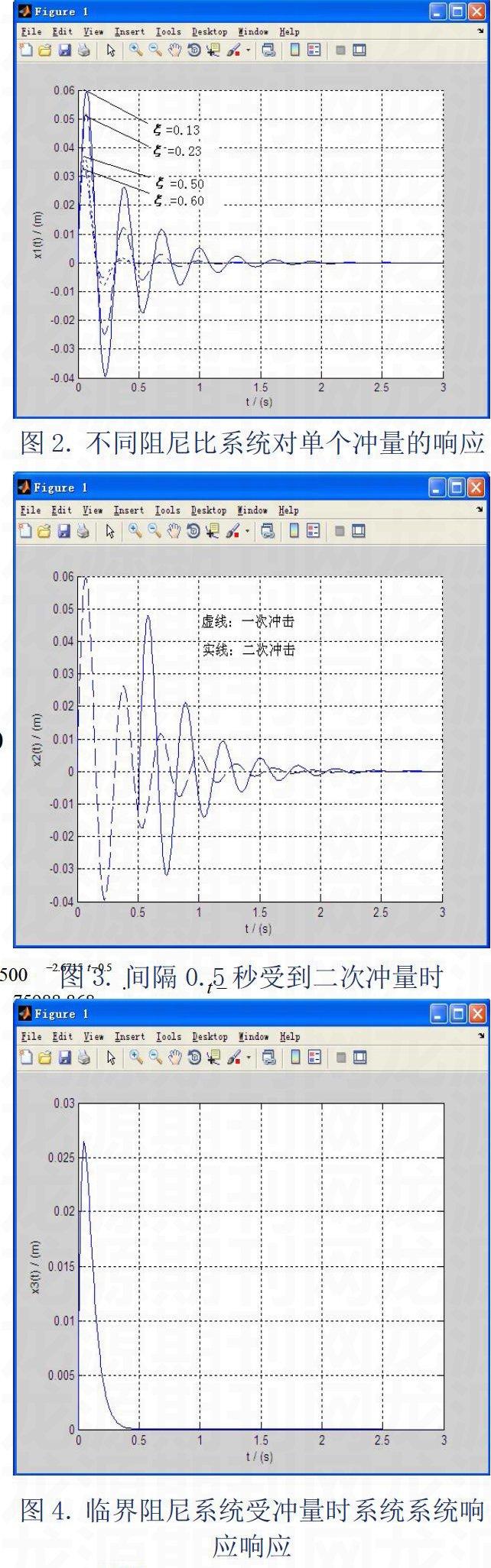
利用MATLAB的Plot等函数功能绘制阻尼比分别为0.13，0.23，0.50，0.60，受到相同的冲量F时系统响应对比曲线如图2所示；同一阻尼系统（阻尼比0.13）间隔半秒受到相同大小冲量F时系统响应曲线如图3所示；临界阻尼系统受到单个冲量F时系统响应曲线如图4所示。从图3可见，在同一冲量作用条件下，较小阻尼系数的系统响应幅度较大，能量衰减地较慢，作用到较大阻尼系数的系统所引起的交变应力幅能量会在较短时间内被衰减掉，因而会较大幅度地改善主梁零部件所受交变疲劳应力的破坏，特别地，当系统受到连续冲量作用的条件下，第二次振动能量势必会与第一次振动相叠加，两次振动的相位角也未必相同，这样会更进一步增强振动的幅度与延长衰减周期，使振动加剧，如图3所示。而对于系统阻尼系数接近于临界阻尼系数时，系统受到同样冲量F时所产生的振动振幅会大幅度地减小同时该能量会很快地被衰减掉，如图4所示，极大地减小起重机主梁结构受到的应力幅和衰减周期，有效地延长构件使用寿命。

4.结论

（1）对起重机进行简化建模，求解出受冲量作用的系统响应函数

（2）利用MATLAB软件绘制系统受到单个及间隔性地冲量作用下系统阻尼

与响应的仿真曲线图。

（3）仿真曲线分析，找出阻尼与系统响应对应关系，为指导起重机主梁寿命

优化设计提供更为精确的计算方法。

参考文献：

[1]成大先等.机械设计手册（第五版）：单行本—机械振动 机架设计[M].北京：化学工业出版社，2010.

[2]胡海岩等.机械振动基础[M].北京：北京航空航天大学出版社，2005.

[3]全国起重机械标准化技术委员会. GB/T3811-2008 起重机设计规范释义与应用[M].北京：中国标准出版社，2008.

作者简介：

晋跃（1982—），男，硕士研究生，研究方向：起重机械安全检验。