沪深300股指期货日历效应研究

陈雁

【摘要】 本文将沪深300股指期货作为研究的对象，研究其日历效应。我们用同花顺软件选取样本数据，并且应用EXCEL、SPSS、EVIEWS等软件对数据进行处理。在此基础上，运用ARCH模型和GRCH模型进行实证检验，最后发现沪深300股指期货存在收益率在星期一显著为负，在星期五显著为正数的周内效应的结论。并在该研究结论的基础上提出了针对性的政策建议。

【关键词】 沪深300股指期 货日历效应 ARCH模型

一、引言

股指期货在我国已经经历了四年多发展，沪深300股指期货不仅开启了中国金融期货的时代，也丰富了我国在证券市场上的交易种类，使得金融市场更加健全，但仍然存在着各种市场异象。这些异象的存在一方面严重影响了市场的有效性，另一方面也给投资者带来巨大的风险。其中主要的异象之一就是日历效应（Calendar Effect），即市场收益率在某一时间段内高出其他时间段，如果在此时进行交易就可以获得较高的收益。本文所研究的样本数据选取了2010年5月4日至2014年7月5日内所有交易日的收盘价，这段时间是2008年金融危机后开始走向经济复苏时段，也是沪深300股指期货推出到现今的大体时间。在研究时间范围内，指数大体是呈下降的趋势，但是走向平缓，没有太大的波动。采集一组相同背景下具有相似特征的样本，这便于开展研究，也使得研究结果更具可信度。

二、文献综述

美国学者Osborne（1962）最早研究周日效应的。后来Cross（1973）和French（1980）运用美国500家上市公司股票指数的标普500指数（S&P 500 Index）进行了日历效应研究和实证检验。他们的研究结果表明在美国的股票市场中存在着最高平均收益率出现在星期五的周内效应。在国内，俞乔较早对上海和深证股市进行研究，研究发现，周末效应同样存在于上海和深证股票市场。徐国栋等人研究结果表明，季节效应明显的存在于上海股票市场，而在深圳股票市场并不明显。郭彦峰等对沪深300指数进行了相关的研究，他们的研究结果显示指数中存在周内日历效应。

三、模型设定与实证检验

1、样本选取

本文通过同花顺软件，收集了沪深300股指期货从2010年5月4日到2014年7月5日每个交易日的成交量和收盘价作为研究样本，有效样本各为1010个。然后再对数据进行对数处理，得到每个交易日的对数收益率和成交量变化率，有效样本数各为1009个。本文在计算的过程中为了减少检验误差对所有的样本数据进行了对数处理。由于对数收益率和成交量变化率都比较小，所以将数据扩大100倍，目的是方便计算和统计。

分别对收盘价和成交量进行对数处理，计算公式如下：

其中rt代表的是t日当天的对数收益率，pt代表的是t日当天的收盘价格，pt-1代表的是t日前一天的收盘价格，即t-1日的收盘价格。dcjlt代表的是t日当天的成交量变化率，cjlt代表的是t日当天的成交量，cjlt-1代表的是t日前一天的成交量，即t-1日的成交量。

2、数据处理

对每个交易日的对数收益率做简单的描述性统计分析，得到表1如下：

从表1的描述统计可以看出：对数收益率平均值在星期三和星期五时都是正数，其中星期五的平均值最大，为0.163，而其余三日的平均值为负数，其中星期四的平均值最小，为-0.2572；从偏度来看，星期三和星期四这两天都是往右偏，其他三日均往左偏；从峰度来看，星期五的峰度为4.0168，大于3，表示比正太分布要陡峭一些，其余四日峰度均比3要小，所以比正太分布平坦。再从JB统计量可以看出，每个交易日以及总体的对数收益率均不服从正态分布。

对每个交易日的成交量变化率进行简单的描述性统计分析，得到表2如下：

从表2的描述统计可以看出：星期一和星期四这两日的成交量变化率平均值为正数，其中星期一的最大，为3.1675。其余三日均为负数，其中星期三的最小，为-1.9791；从偏度来看，成交量变化率在一周中均往右偏。再从JB统计量可以看出，每个交易日以及总体的成交量变化率均不服从正态分布。

3、ARCH模型检验

借鉴陈龙的研究，本文构建如下ARCH模型。

为了验证ARCH效应是否存在于一个模型的残差中，通常可以采用拉格朗日乘数检验（ARCH LM检验）以及残差平方相关图检验这两种方法。本文选取了在本文研究时间范围内的各交易日收盘价作为样本序列，并对该样本序列进行相关的验证。将样本序列进行对数处理是为了减少误差。

初步设定模型的基本形式为：

其中因变量Y所代表的是spt，表示在t日当天的对数收盘价；自变量X代表spt-1，表示在t-1日当天的对数收盘价。

（1）单位根检验

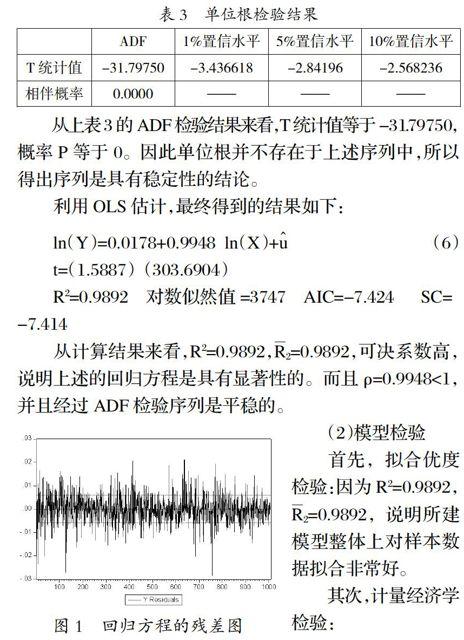
如果序列中存在单位根，那就说明这不是一个平稳的序列，假如对不平稳的序列进行回归分析，会使得结果存在误差，因此要对序列进行单位根检验。检验结果见表3。

从上表3的ADF检验结果来看，T统计值等于-31.79750，概率P等于0。因此单位根并不存在于上述序列中，所以得出序列是具有稳定性的结论。

利用OLS估计，最终得到的结果如下：

从计算结果来看，R2=0.9892，R2=0.9892，可决系数高，说明上述的回归方程是具有显著性的。而且？籽=0.9948<1，并且经过ADF检验序列是平稳的。

（2）模型检验

首先，拟合优度检验：因为R2=0.9892，R2=0.9892，说明所建模型整体上对样本数据拟合非常好。

其次，计量经济学检验：

最后，异方差检验：通过对图1的观察，可以发现在残差图中产生了波动成群的现象，说明模型可能存在异方差。因此，继续进行ARCH LM检验，最终得到滞后七阶的检验结果见表4。

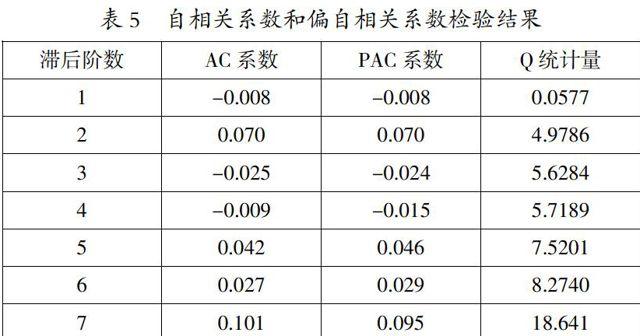
此时的概率P值等于0.0111，即在5%的显著水平下拒绝回归方程中不存在ARCH效应的原假设，说明了ARCH效应存在于回归方程的残差序列存中。此外，我们从AC系数和PAC系数也能够验证上诉结论（见表5）。

从表5可以看出，无论是AC图还是PAC图，在滞后二阶和七阶时都超出了區间范围，其他阶都在区间范围内。因为在滞后二阶和七阶的AC系数和PAC系数均显著不等于0，并且相对应的Q统计量较为显著，因此可以得出：ARCH效应存在于模型的残差序列中。

四、结论与政策建议

既然沪深300股指期货存在着周内日历效应，说明该市场并不是有效的市场。为了提高投资收益率，投资者在进入或者退出投资市场时，可以结合实际情况来利用已掌握到的日历效应信息，通过日历效应来改善自身的投资策略，从而更好的规避风险。比如，在星期五的平均收益率最高，就可以在其他平均收益率低的交易日进行买入操作，或者在星期五进行卖出操作。当然，我们并不能单单笼统的运用日历效应来进行市场操作，因为市场是多变的，要预测市场的变动需要考虑到多种因素的综合作用。

（注：本文系广西哲学社会科学十二五规划项目（项目编号：11EMZ014）和桂林旅游学院科研项目（项目编号：2011QN01）。）

【参考文献】

[1] 徐国栋、田祥新、林丙红：中国股市季节效应实证分析[J].广西财政高等专科学校学报，2004（10）.

[2] 郭彦峰、魏宇：我国股指期货标的指数的日历效应研究[J].西南交通大学学报（社会科学版），2007（5）.

[3] 郭彦峰、黄登仕、魏字：上海期货市场收益和波动的周日历效应研究[J].管理科学，2008（4）.

（责任编辑：谌盼）