Elman网络在养殖水体氨氮预测中的应用研究
汪翔 何吉祥 佘磊等
摘要利用2014年6~10月养殖塘口记录的饲料投喂量、水体溶解氧量、水温、气温、浊度、降雨量作为模型输入,检测的氨氮作为模型输出,建立了用于养殖水体氨氮模拟的Elman网络。利用2014年11月的观测数据,对模型的模拟能力进行了检验。结果表明:建立的养殖水体氨氮预测模型,可以较好地模拟水体中氨氮浓度的变化趋势,模拟的绝对误差平均值为0.016 mg/L,决定系数R2为0.74。说明Elman网络建立的预测模型在养殖水体氨氮含量变化预测中具有强非线性动态描述能力,对养殖水体中氨氮的预测有较好的适用性和预测精度。
关键词养殖水体;水质预测;Elman網络;非线性系统
中图分类号S951.2文献标识码
A文章编号0517-6611(2015)31-365-03
Application of Elman Neural Network in Aquaculture Water NH3N Prediction
WANG Xiang, HE Jixiang, SHE Lei et al
(Fisheries Research Institute, Anhui Academy of Agricultural Sciences, Hefei, Anhui 230031)
Abstract Elman artificial neural network model was developed to predict the change of water NH3N in aquaculture pond. The indexes including feed ration, dissolved oxygen in water, water temperature, air temperature, water turbidity, rainfall were recorded and chosen as the input variables, while the NH3N content in the corresponding pond was chosen as output variable. The above data were collected everyday from June to October in 2014. They were used to develop model in this test, and the data collected in November of 2014 were chosen to evaluate the developed model. The results showed that the changing trend of water NH3N in aquaculture pond could be simulated well by the model, the predictive absolute error mean was 0.016 mg/L, and R2 was 0.74. The prediction model based on Elman neural network had a strong ability to describe the nonlinear dynamic changes of NH3N content in aquaculture water, and it showed the good adaptability and accuracy in practical application.
Key words Aquaculture water; Water quality forecast; Elman neural network; Nonlinear system
水体中的氨氮是氮循环中的组成部分,其对水产养殖对象具有生物毒害 [1]。氨氮对水生生物的危害主要是指非离子氨,非离子氨进入水生生物体内后,对酶水解反应和膜稳定性产生明显影响,使其表现出呼吸困难、不摄食、抵抗力下降、惊厥、昏迷等现象,影响水生生物的生理、生化指标与生长状况,严重时可导致养殖生物大批死亡,造成经济损失[2]。因此,深入研究养殖水体中氨氮变化规律,准确预测其变化并将预测结果应用于指导生产过程,对提高养殖产品质量、提高养殖效益和防止鱼病的发生具有重要意义。
池塘中氮主要来源于肥料和饲料,饲料中的氮有60%~70%被排泄到水体中,而进入水体中的氮一般以氨的形式存在。在正常条件下氨氮会通过亚硝化细菌转化为亚硝酸盐,在环境条件发生变化时硝酸盐又会被兼性厌氧细菌还原为氨氮[3]。影响水体中氨氮浓度的因素很多,如pH、水温、溶解氧、硝化细菌数量、化肥、农药及抗生素使用都影响水中氨氮的变化,所以养殖水体中氨氮变化趋势具有明显的非线性,没有直观规律可循。而水体中氨氮变化涉及水化学、生物动力、微生物、气象等诸多内容,其中某些变化原理人们还尚未认识清楚,很难从机理上建模。目前解决此类问题的代表性方法有GM(1,1)灰色模型[4-5]和BP神经网络[6-7],但也仅限于环境水体指标分析预测。理论和实践显示,当采集的原始数据呈指数规律变化时,灰色预测模型的预测精度较高,但对于序列变化不呈指数规律时,预测会出现较大偏差[8];而BP神经网络模型训练速度过慢、外部噪声敏感,预测结果呈现出不稳定性。该研究选择Elman网络建立氨氮预测模型,通过采集和处理数据,训练预测模型,把模拟输出数据与实测数据比对分析,得出较为理想的结果,在实际应用中取得了较好的效果。
1Elman网络原理
Elman网络(Simple Recurrent Neural Network) 全称简单递归神经网络,是在传统 BP 网络的隐含层上增加一个承接层 ,作为内部延时, 达到记忆的效果,从而使系统具有广泛的泛化能力。因此它可以反映系统历史状态信息,是一种有记忆功能的、体现历史时间变化的神经网络。与BP神经网络简单的静态神经网络相比,Elman网络能够更好地描述动态时变系统特性,从而更有效地实现复杂动态系统建模。
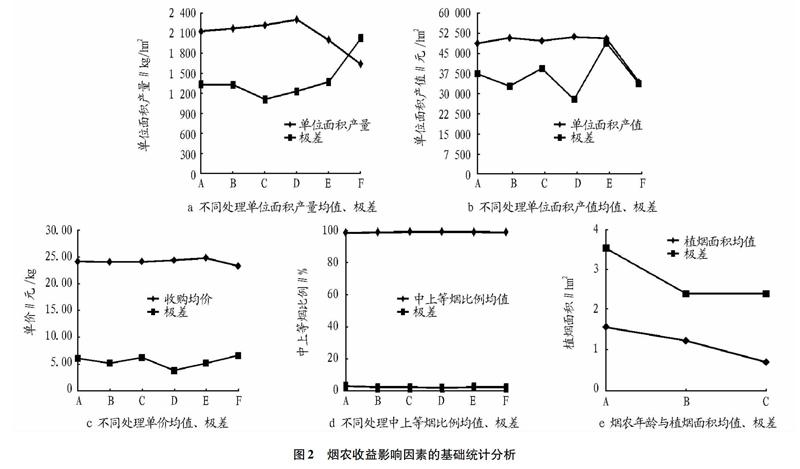
Elman 型神经网络分为4层:输入层、隐藏层、承接层和输出层。输入层和输出层为信号的输入和输出,隐藏层为激发函数 ,承接层用来储存隐藏层上一次的输出值。Elman模型结构见图1。由图1的 Elman 型神经网络结构组成可知 , 隐藏层的输出和输入都通过承接层的延迟和存储。这种自联方式使系统对历史状态的数据具有敏感性,网络的内部反馈结构提高了模型处理动态信息的能力,从而达到了动态建模的目的。
2检验函数
为了对水体氨氮变化趋势模拟输出结果进行实测值对比检验, 该文采用均方误差MSE(Mean Square Error)、绝对误差AE(Absolute Error)、决定系数R2(Coefficient of Determination)等数据分析方法对Elman网络的模拟精度进行了评价。上述误差函数参考相关文献[9]进行计算。
3数据采集
2014年6月28日~11月21日,在安徽省农业科学院岗集养殖基地选择4个草鱼苗种养殖塘口,养殖塘口均为长方形,220 m×45 m,东西向,塘口面积为9 900 m2。每天上午10:00对养殖水体水温、气温、浊度、降雨量、pH、溶解氧、风速、日照、氨氮、亚硝酸盐等14项指标进行数据分析和采集。同时记录每个塘口水位、养殖品投放量、饲料投喂量、用药量等生产日志。
3.1水质检测
每个养殖塘口设置4个采样点,用0.5 L采水器采集水面下0.5 m处水体,将采集水样均匀混合后,进行水质检测。用WGZ-1B数显浊度仪测定浊度;用DZ-A多参数水质分析仪测定氨氮、亚硝酸盐;用JPBJ-608型溶解氧测试仪测定溶解氧;用GDYS-101SV硫化物测定仪测定硫化物;用AZ8601PH测试仪测定pH。
3.2气象记录
在观察点建设无线电子室外气象站(德国TFA 35.1067 VEGA WS-1600IT IT),将风速传感器安装在离地面2 m高度处,将大气温湿度传感器和雨量计传感器安装在离地面0 m高度处。每3 h自动记录气温、湿度、气压、降雨量、风速。
4基于Elman网络建立养殖水体氨氮预测模型
4.1建模样本
根据水体中氨氮的产生过程和影响因子,项目组对观察塘口记录了气温、水温、气压、光照、风速、投喂量、降雨量、浊度、pH、溶解氧、盐度、氨氮、亚硝酸盐、硝酸盐等14项指标。本着模型的输入量数据容易获取原则,经过多元回归分析后选取相关系数较高、易获取的指标为模型输入变量。最终该研究选择2个参与细菌硝化作用的指标(饲料投喂量、溶解氧)和4个环境变化指标(水温、气温、浊度、降雨量)共计6个因子作为模型的输入变量,模型的输出变量用水質监测获得的氨氮数据进行校正训练。2014年6~10月采集分析的数据为建模样本(n=126),11月采集分析的数据为预测样本(n=20)。在网络学习过程中,为便于网络的训练,以及更好地反映各因素之间的相互关系,在样本使用前对样本数据进行了归一化处理:
X′i=Xi-XminXmax-Xmin
式中,Xi和X′i分别代表归一化前后的第i个向量元素,Xmax和Xmin分别代表向量的最大和最小值。
4.2网络参数的确定
Elman网络主要由输入层、隐藏层和输出层及承接层构成。由于预测模型的建模样本是由6个输入变量和1个输出变量构成,因此输入层和输出层的神经元个数分别为6和1。隐藏层神经元个数的选取由多种因素决定,目前没有成熟的理论依据,只能根据设计者的经验,通过多次试验来确定。该研究对隐藏层神经元个数采用试错法来确定。分别构建了隐藏层神经元个数从5~20的模型,由于输入权值和阈值影响着神经网络性能变化,所以每个模型训练10次,分别记录训练结果的均方误差MSE和决定系数R2。
由图2和图3可以看出,MSE和R2在初始阶段随着神经元个数的增加而分别增大和减小,当神经元个数超过10后,随着其个数继续增加,MSE和R2表现出相反的趋势。这说明隐含层神经元个数过少时,模型会出现拟合不足,容错性差,识别新样本能力低等问题;隐藏层神经元个数过多则会增加模型的迭代次数和训练时间,导致模型过度拟合,降低模型的泛化能力,从而造成模型预测能力下降,这与前人研究结果[10]一致。因此该研究将隐藏层神经元个数选为10。
4.3网络训练
该研究选用贝叶斯正则化算法训练Elman网络,将网络权值均方与误差均方的加权作为性能函数,在保证网络均方误差尽可能小的前提下,有效地控制网络复杂程度的增加,从而获得较好的泛化性能,提高网络推广能力。在MATLAB_R2012b环境下,调用newelm函数构建网络,建模样本按照7.0∶1.5∶1.5比例[11]分为88个训练样本、19个验证样本、19个测试样本,传递函数设定为tansig函数,训练函数设定为trainbr函数,权值自适应学习函数设定为learngdm函数,性能函数采用MSE。网络学习速率0.01,学习速率增量因子为1.2,学习速率减小因子为0.6, 动量常数取1.1。网络经过165次训练,后构建了网络结构为图4所示的Elman网络。
5结果与分析
5.1网络预测能力分析
将预测样本带入训练好的Elman网络氨氮预测模型进行预测,结果见图5。预测结果存在局部的高估或低估现象,但总体上模拟的氨氮浓度变化趋势与实测值基本相同,实测和模拟的数值十分接近。网络预测结果的绝对误差AE的最大值为0.03,最小值为1.4×10-4,平均值为0.016;均方误差MSE为5.2×10-4;决定系数R2为0.74。项目组利用BP网络建立的预测模型决定系数R2为0.66,低于利用非线性自结合的时间序列网络建立的水体氨氮浓度时间序列预测模型的决定系数0.74,说明预测模型模拟的精度和适用性都较高。
5.2网络适应性验证
构建Elman网络氨氮预测模型数据源取自4号观察塘口。将1、3、4号塘口的数据带入以4号观察塘口数据为建模样本所构建的氨氮预测模型中进行预测,结果见表1。由表1可以看出,虽然1、2、3号塘口预测结果
误差比4号塘口预测结果误差大,但预测误差均在该研究的误差期望值内。根据研究,氨氮对鲢、鳙鱼苗的半致死浓度
分别是1.106 mg/L和0.559 mg/L;草鱼种最大允许氨氮浓度为0.099 mg/L[12];杂交罗非鱼最大允许氨氮浓度为0171 mg/L[13];保持鲫鱼碱性磷酸酶(AKP)和溶菌酶(LSZ)活力的氨氮临界值分别为0.70、0.56 mg/L[14]。因为预测误差的数量级远小于养殖水体划分的氨氮临界值数量级,所以预测误差对水体中氨氮的风险评判影响甚小。
6结论
养殖水体中氨氮的变化趋势复杂多样,该研究利用Elman网络建立了养殖水体的氨氮时间序列预测模型,并对氨氮浓度变化趋势进行了短期预测。结果表明:Elman网络以其良好的非线性映射能力,在非线性的氨氮时间序列预测中有着较高的预测精度。该研究利用4号塘口数据构建的Elman网络氨氮预测模型,在1、2、3号塘口进行了验证,结果表现了模型在同一区域内有良好的适应性。
参考文献
[1]
谢江宁,阎喜武.总氨对水生生物毒性的研究进展[J].科学养鱼,2008(8):4-5.
[2] 蔡继晗,沈奇宇,郑向勇,等.氨氮污染对水产养殖的危害及处理技术研究进展[J].浙江海洋学院学报(自然科学版),2010,29(3):167-172.
[3] 周超,高乃云,楚文海,等.水体中亚硝酸盐生物毒性和去除的研究进展[J].给水排水,2011,37(5):104-108.
[4] 胡惠彬.GM(1,1)模型在地表水濃度预测中的应用[J].中国环境监测,1993,9(4):45-46.
[5] 胥冰,韩小勇.淮河干流水环境评价及其趋势分析[J].水资源保护,1998(2):10-17.
[6] 王晓萍,孙继洋,金鑫.基于BP神经网络的钱塘江水质指标的预测[J].浙江大学学报(工学版),2007(2):361-364.
[7] 王泽平.基于GA-BP与多隐层BP网络模型的水质预测及比较分析[J].水资源与水工程学报,2013(3):154-160.
[8] 李如忠.水质预测理论模式研究进展与趋势分析[J].合肥工业大学学报(自然科学版),2006(1):26-30.
[9] DUAN W,YANG L X.An improved BP neural networks applied to classification[J].Energy procedia,2012(13):7065-7069.
[10] COULIBALY P,ANCTIL F,ARAVENA R,et al.Artificial neural network modeling of water table depth fluctuations[J].Water resources research, 2001,37(4):885-896.
[11] 席裕庚.预测控制[M].北京:国防工业出版社,1993:52-61.
[12] 梁健,王红权,金柏涛.氨氮对草鱼幼鱼的急性毒性试验[J].科学养鱼,2013(11):47-51.
[13] 肖炜,李大宇,徐杨.慢性氨氮胁迫对吉富罗非鱼幼鱼生长、免疫及代谢的影响[J].南方水产科学,2015,11(8):81-87.
[14] 江敏,黄宗群,彭自然.异育银鲫氨氮排泄与耗氧的研究[J].上海水产大学学报,2007,16(1):28-32.

