热电制冷热传导模型及其在非均匀热流中的应用*

朱仁江 潘英俊† 蒋茂华 范嗣强 张鹏

(1.重庆大学 光电技术及系统教育部重点实验室，重庆400044;2.重庆师范大学 物理与电子工程学院，重庆401331;3.重庆市高校光电材料与工程重点实验室，重庆401331)

现代科技发展促使半导体光电子器件功率密度不断提高［1］，晶片的耗散热流密度急剧增加，如半导体薄片激光器的热流密度可达万瓦每平方厘米的水平［2］.由于半导体材料和应变量子阱对温度的敏感性，热堆积不仅影响器件的诸多性能［3］，其内部应力产生的蠕变还会加速器件老化和失效［4］，因而对半导体功率器件的热管理结构进行优化设计，掌握散热系统温度场分布对器件封装具有非常重要的意义.

热电制冷(TEC)具有寿命长，无振动、易于集成封装和温控精度高等优点，基于热电制冷(半导体制冷器)的热电耦合特性，其制冷性能受输入电流、冷热端面温度、温差及内部热电偶参数等因素影响.目前国内外［5-7］对热电制冷的研究主要是假定热流呈一维均匀分布，建立热传导的等效电路模型，进而以电路理论研究含TEC 的散热系统特性.文献［8］中进一步提出将TEC 分割成若干子域近似解决TEC 端面温度非均匀性问题. 对于横向尺寸远小于散热器的光电功率器件，采用温度场数值计算更能直观准确地反映系统传热特性.然而目前TEC 热传导模型［9-10］的准确性不仅依赖于属于商业秘密的热电偶物理和几何参数，而且冷热端面的内热源大小受电流、温度和温差影响［11］，对冷热端面温度非均匀分布的边界条件进行数值分析存在较大困难［12］.出现上述问题的主要原因是TEC 特性不符合标准的传热学规律，基于此，文中将根据TEC 制造商提供的标准参数，建立不依赖于端面温度和热电偶材料属性的新型热传导模型，利用该模型计算含TEC的点热源散热系统温度场特性，并对该散热系统做共性分析.

1 热电制冷的热传导模型

如图1 所示，TEC 通常由热电偶、铜导流片和氧化铝陶瓷绝缘板构成，利用导流片实现热电偶电学串联和热学并联结构.当TEC 通过电流I 时满足以下关系式［12］:

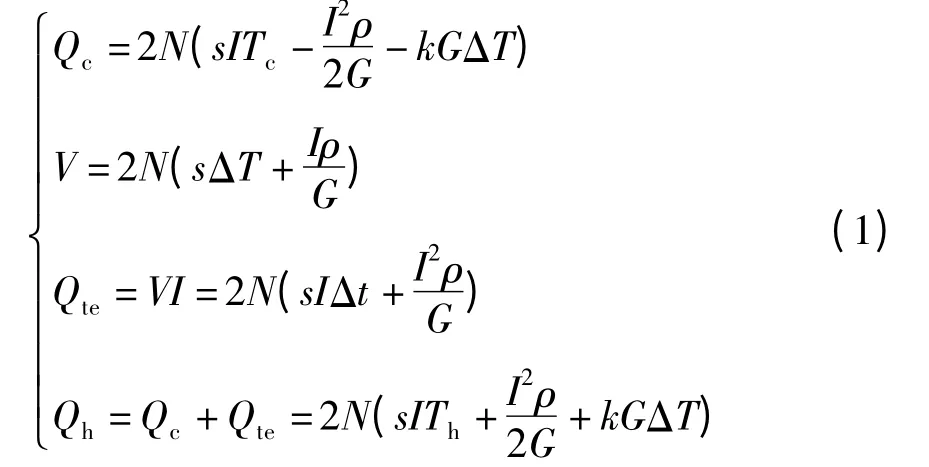
式中，Qc为TEC 冷面的制冷量，N 为热电偶对数量，s 为热电单元的赛贝克系数，ρ 为电阻率，G 为热电偶几何因子参数，k 为热电偶热导率Tc为冷端面面温度，Th为热端面温度，ΔT 为端面温差ΔT =Th-Tc，V 为端电压，Qte为输入电功率，Qh为热面的发热量.

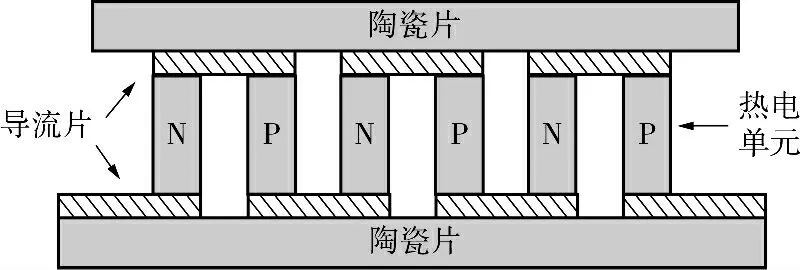
图1 热电制冷器结构图Fig.1 Structure diagram of the thermoelectric cooler

上述表达式所含的热电偶物性参数s、ρ、G 难以从制造商获取，可定义TEC 模型的宏观参数电阻Rm、热导Km和赛贝克系数Sm如下:

文献［13］研究表明，式(2)可以使用TEC 制造商提供的标准参数而表示为

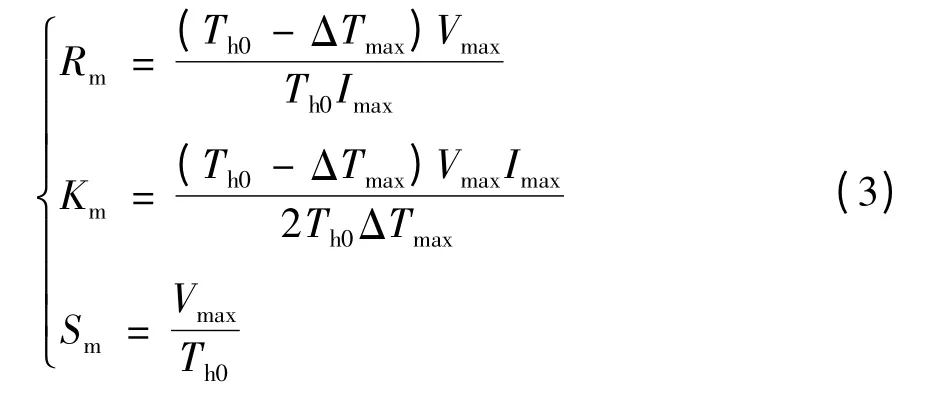
式中，Th0为制造商产品测试数据中热端面温度，ΔTmax为制冷量为零时最大允许输入电流Imax所对应的冷热端面最大温差，Vmax为取ΔTmax时对应的TEC 输入电压.

根据式(2)、(3)，可将式(1)改写为

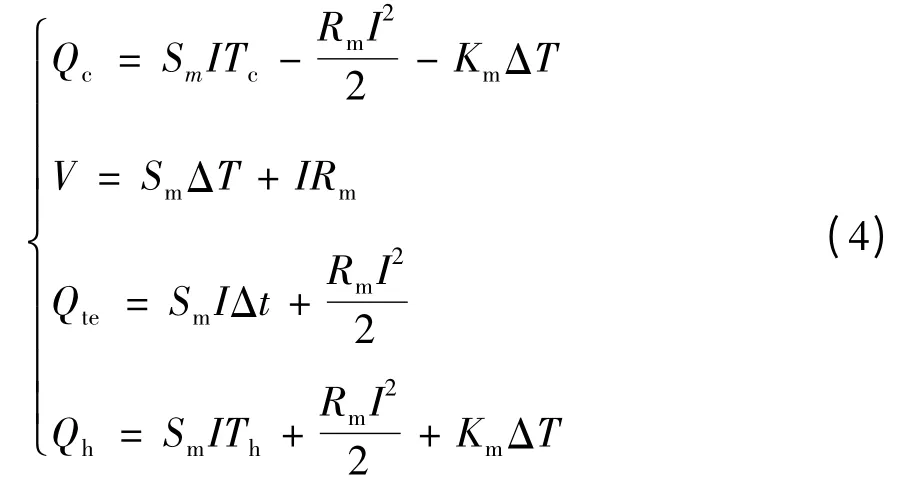
式(4)表明可利用制造商提供的标准参数描述TEC的宏观热电耦特性，为实际应用中TEC 的选型和等效电路模型提供参考.

用于TEC 温度场分析的热传导模型通常是将式(4)中Qc、Qh去掉热传导项后作为内热源，该内热源由于受温度、电流和温差等参数影响，在数值分析时通常需要假设表面温度为常量，以减少迭代运算次数并满足变量间的约束要求，因而基于这种模型分析点热源热扩散引起的TEC 端面温度不一致现象时将更加复杂.

根据热电制冷的物理效应可将式(4)改写为

式中，前两个方程分别描述了TEC 冷热端面的帕尔帖效应，其余两方程分别为焦耳效应和傅里叶效应.根据TEC 的热电耦合特性(如图1 所示)，焦耳热在半导体热电偶电臂上均匀分布，而帕尔帖效应位于热电偶电臂与导流片接触面，由于导流片的热导率远大于热电偶，且厚度薄，可将帕尔帖效应视作导流层内热源.同时导流片的电阻率远小于热电偶，可将焦耳效应视作热电偶层内热源. 通过将焦耳效应和帕尔贴效应分离简化TEC 内热源的表达式，同时将模型各层介质热学参数做均质化处理，傅里叶效应已包含在导热微分方程中，基于此可建立如图2 所示的TEC 稳态热传导模型.

椭圆型偏微分方程的基本形式为

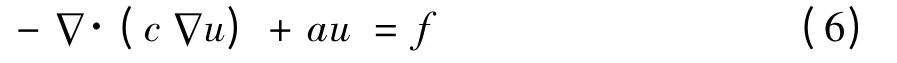
当零阶导数项系数a 为0 时，方程即为稳态导热微分方程，其中自由项f 为内热源密度表达式.

令VS和VJ分别为导流层和热电偶层体积，其稳态导热微分方程为

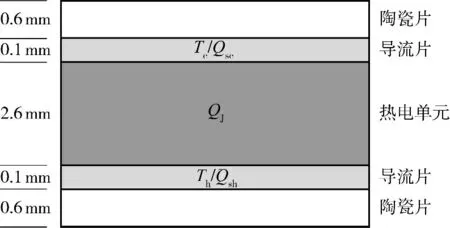
图2 热电制冷的热传导模型Fig.2 Heat transfer model of thermoelectric cooler

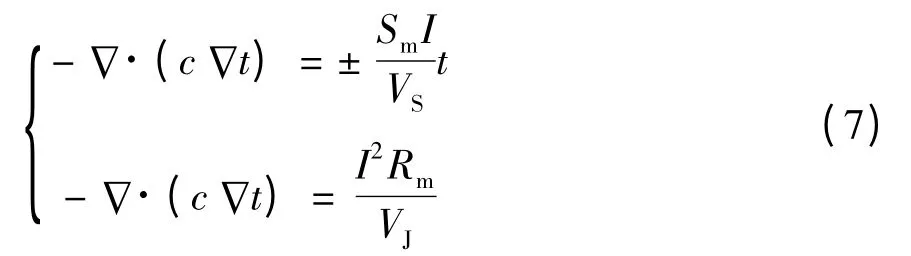
式(7)中自由项的正负号分别对应放热和吸热过程，其中第一个方程中自由项由于帕尔贴效应包含温度变量，自由项转变成为零阶导数项，不再是标准热传导方程，因而用传统热传导模型分析TEC 温度场分布存在较大困难. 若将式(7)作为椭圆型偏微分方程求解时，则可屏蔽第一个方程中内热源的温度参数.同时式(7)中各项系数不依赖于制造商产品的物理和几何参数，在特定输入电流下，只需要确定边界条件即可求解其温度场分布，模型可较为准确分析含TEC 制冷器的小尺寸功率器件的温度场分布特性.

2 结果与讨论

2.1 TEC 热传导模型可靠性验证

Ferrotec 公司的热电制冷产品950/127/085B［14］的性能特性参数如表1 所示，由于TEC 内部几何参数未知，根据产品的外观数据，模型中各层厚度取经验值如图2 所示，并由式(3)计算模型所需参数.在模型设定的几何结构下，设各层为各向同性均匀材料，其中热电偶层热导率由热阻表达式计算.根据导流层和陶瓷绝缘导热层材料构成，其热导率分别设定为400 和29 W/(m2·K).图3(a)是热端面固定为50℃时，在冷热端面不同温差下TEC 制冷量随输入电流变化的制造商测试数据，图3(b)是在同样条件下对模型利用COMSOL 软件进行有限元分析时所得数据.对比发现，模型在电流小于6 A时能很好地拟合测试曲线，在继续增大电流输入时模拟曲线整体较测试曲线略有抬升. 如果在大输入电流时将Rm增加5%，则模拟曲线基本能和测试曲线重合，这可能是式(4)中忽略了部分非线性效应引起.此外利用该模型均能较好地拟合其他型号的热电制冷器性能曲线，反映出模型具有极强的适应性.

表1 热电制冷器的产品数据Table 1 Supplied data of TECs

2.2 点热源散热模型

如图4 所示是含TEC 的点热源散热系统结构示意图，其中TEC 采用前述的9500/127/085B 型，各层几何数据与热力学参数如表2 所示. 由于TEC热端面热沉风冷和水冷散热模式均涉及导热和对流过程，其区别在于等效换热系数不同，同时文中不讨论TEC 热沉部分的温度场分布，因而对这两种散热模式统一处理.模型中不考虑各层间的接触热阻，除特别说明，模拟热源设定功率为12 W，TEC 热沉下方采用第3 类边界条件，热交换系数设定为1 kW/(m2·K)，环境温度设定为300 K，其余边界做绝热处理.

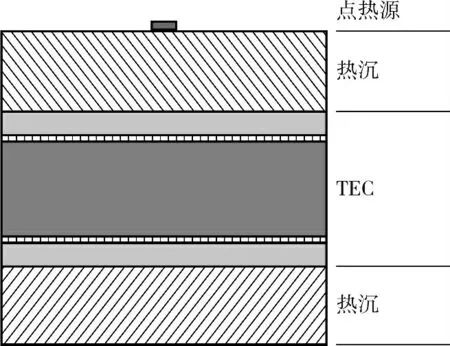
图4 点热源散热系统结构图Fig. 4 Schematic diagram of the dissipation system with point heat source

表2 散热系统各部分参数Table 2 Module parameters of the dissipation system

图5 是热源功率为20 W、TEC 制冷电流为3A时的温度场分布图. 从三维图中可清晰观察到中心的方型模拟热源区温度最高，温度沿热源热沉表面呈现明显近似圆形的下降区域，大部分处于温度最低点的热沉颜色基本一致，表明TEC 温控的点热源散热系统中热沉优化设计的重要性.图5(b)为温度场的中心切面图，其中横向只保留中心的12 mm 宽度.从图中可观察到高热流密度的热源区域温度变化最快，其等温面沿热源中心近似半圆形向外扩展.同时点热源的非均匀热流使得TEC 端面出现了明显的温度分布变化区间，显示出在非均匀热流分析中考虑TEC 端面不同区域温度差异的重要性.基于此，文中在模型结构不变的情况下，进而讨论点热源散热系统的一些共性问题，同时考虑TEC 温控特性，文中模拟在距离热源中心10 mm 处放置温度探头，检测系统温度变化.

图5 含TEC 的点热源散热系统温度场分布Fig.5 Temperature distribution of the dissipation system with TEC-included point heat source

2.3 热交换系数对功率器件温度的影响

针对不同应用环境TEC 热沉的散热模式不同，图6 中考察了散热系统热交换系数对热源最高温度和探头温度的影响，其中横轴采用了对数坐标以适应换热系数大范围变化. 传热的第3 类边界条件表达式可转换为

式中，t|S为热沉边界温度，tf为环境温度. 尽管TEC内热源密度q 和端面温度相关，式(8)仍反映出TEC热沉温度会随热交换系数呈近似反比关系. 从图中可以看出两条曲线随热交换系数增大快速下降，当热交换系数大于3 kW/(m2·K)后，曲线趋于饱和.经计算两条曲线温差恒定保持为21.6 K，表明热交换系数的改变仅使得系统温度发生平移. TEC 功效是通过提供冷热端面温差实现，图6 显示过低的热交换系数会严重降低TEC 功效，这在风冷散热设计中需认真考虑.对于强制水冷散热模式，其热交换系数往往大于1 kW/(m2·K)，将有助于提升TEC性能.

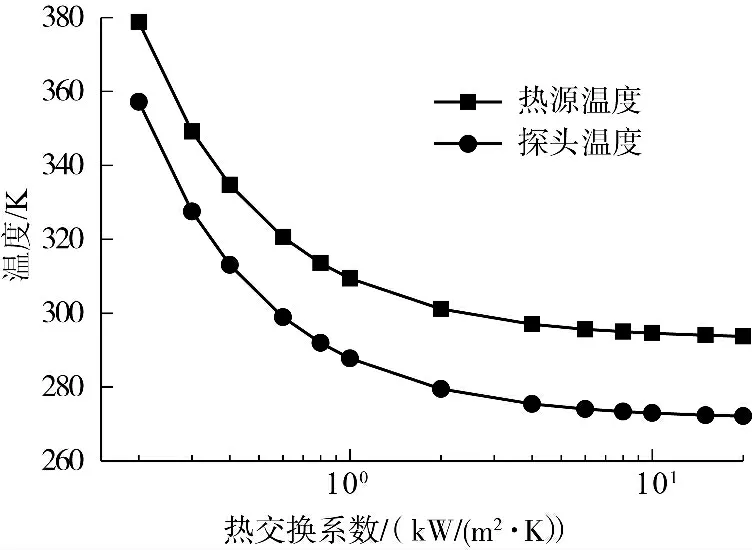
图6 热交换系数对温度的影响Fig.6 Effect of heat transfer coefficient on temperature

2.4 制冷电流对功率器件温度的影响

图7 所示为不同热交换系数下功率器件最高温度随TEC 制冷电流的变化曲线，所有曲线都有最低点，表明在一定的热交换系数下TEC 可能存在最优制冷电流.随着热交换系数的增加，其最优电流右移，同时器件温度也明显下降.部分曲线最高温度超过输入电流为0 时的温度，表明不合理使用会导致TEC 器件功能完全失效. 根据式(4)，热源功率一定，较小的制冷电流时冷热端面温差不大，TEC 温度平移能力不强.随着输入电流增大，冷热端面温差扩大，热源温度下降. 但TEC 热端面热流密度也会增加，基于式(8)的温度参考点的TEC 热沉温度也随之上升.当TEC 电流引起的温差和热沉温度上升值相当时就会出现曲线底部. 由于热沉温度上升速率和热交换系数呈反比关系，因而低热交换系数的曲线底部最先出现.研究发现和图6 类似，功率器件的最高温度和探头温度相差始终保持为21.6 ℃，这表明模拟热源功率不变时，通过保持探头温度恒定可实现对功率器件精确控温.

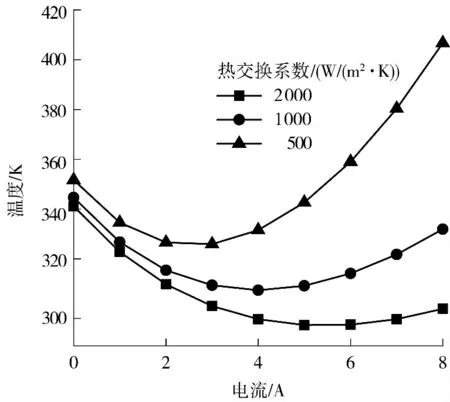
图7 制冷电流对温度的影响Fig.7 Effect of TEC current on temperature

2.5 热源功率对功率器件温度的影响

固定TEC 热交换系数和电流时，如图8 所示功率器件和探头的温度变化与模拟热源功率呈线性关系.模型边界除TEC 热沉下方外均做绝热处理，在模拟热源功率为0 时，功率器件与热源热沉由于没有热流密度分布而不会出现温度梯度，即在图中两条斜线在该位置相交.此时TEC 电流在冷端面产生的制冷量被焦耳热消耗掉，TEC 冷热端面达到该条件下的最大温差.尽管随着模拟热源功率增大，TEC端面温度分布及冷热端面热源会发生相应改变，数值计算结果显示出器件热功耗与其温度仍具有高度的线性关系.此外功率器件和探头的温差也随器件热功耗线性变化，这表明在器件热功耗发生变化时，虽然可通过温控优化TEC 热沉热交换系数和TEC电流保持探头温度不变，但器件温度依然发生变化，使得该条件下精确控温难以实现.

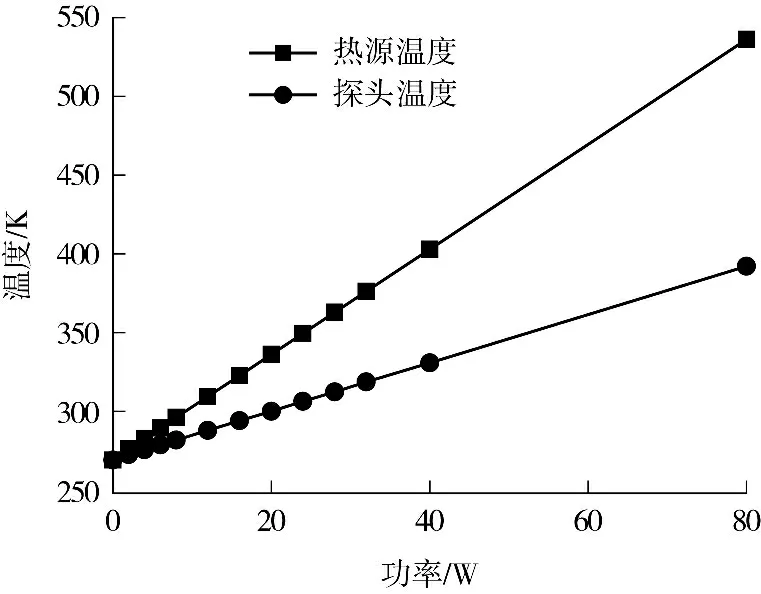
图8 热源功率对温度的影响Fig.8 Effect of heat power on temperature

3 结论

通过分离TEC 中不同内热源的的作用区域，并利用椭圆偏微分方程建立了TEC 新型热传导模型，实现了TEC 端面非均匀温度场的数值分析.同时构建该模型只需要制造商提供的标准参数而不依赖于热电偶的物理和几何参数，通过数据拟合验证了模型具有较强的适应性. 模型的内热源特性仅依赖于输入电流，可有效分析非均匀热流密度下TEC 的传热过程.利用该模型得到了TEC 制冷的小尺寸功率器件散热系统三维和切面温度场分布图，数值分析表明TEC 的制冷性能对热沉热交换系数非常敏感，制冷电流存在最优区间，器件的温度变化与其热功耗成线性关系，当器件热功耗不变时可通过温度探头实现精确控温.

［1］简弃非，李聪.兆瓦级风电变流器IGBT 模块的热特性分析［J］. 华南理工大学学报:自然科学版，2014，42(6):1-6.Jian Qi-fei，Li Cong.Analysis of thermal properties of IGBT modules in MW-level wind power converter ［J］.Journal of South China University of Technology:Natural Science Edition，2014，42(6):1-6.

［2］陈柏众，戴特力，梁一平，等. 用有限元法讨论光抽运垂直外腔面发射半导体激光器的散热性能［J］.中国激光，2009，36(10):2745-2750.Chen Bai-zhong，Dai Te-li，Liang Yi-ping，et al.Finite element analysis of thermal management in optical pumping semiconductor vertical-external cavity surface-emitting laser［J］.Chinese J Lasers，2009，36(10):2745-2750.

［3］Zhang P，Song Y R，Zhang X P，et al.Numerical analysis of thermal effects in InGaAs system vertical-external-cavity surface-emitting laser ［J］. Optical review，2011，18(4):317-323.

［4］薛正群，黄生荣，张保平，等. GaN 基白光发光二极管失效机理分析［J］. 物理学报，2010，59(7):5002-5009.Xue Zheng-qun，Huang Sheng-rong，Zhang Bao-ping，et al. Analysis of failure mechanism of GaN-based white light-emitting diode ［J］. Acta Physica Sinica，2010，59(7):5002-5009.

［5］Lineykin S，Ben-Yaakov S.Modeling and analysis of thermoelectric modules ［J］. IEEE Transactions on Industry Applications，2007，43(2):505-512.

［6］Lineykin S，Ben-Yaakov S.Analysis of thermoelectric coolers by a spice-compatible equivalent-circuit model ［J］.Power Electronics Letters，IEEE，2005，3(2):63-66.

［7］杨明伟，周兆英. 微型热电制冷器非稳态特性的热电模拟研究［J］.红外与激光工程，2008，27(3):432-435 Yang Ming-wei，Zhou Zhao-ying.Transient behavior of micro thermoelectric cooler by equivalent circuit method［J］.Infrared and Laser Engineering，2008，37(3):432-435.

［8］Yang Y T，Wang N，Dong G，et al.Two-dimensional electrical modeling of thermoelectric devices considering temperature-dependent parameters under the condition of nonuniform substrate temperature distribution［J］.Microelectronics Journal，2013，44(3):270-276.

［9］高薪蕙，邓忠民，王静涛.TEC 结构的三维非线性瞬态温度场分析［J］.计算力学学报，2012，28(1):25-30.Gao Xin-hui，Deng Zhong-min，Wang Jing-tao. Three-dimesional nonlinear temperature field analysis of TEC structure［J］. Chinese Journal of Computational Mechanics，2012，28(1):25-30.

［10］杜群贵，邹杰慧，陈水金，等.半导体热电转换单元发电性能的变物性计算模型［J］.华南理工大学学报:自然科学版，2013，41(4):47-53.Du Qun-gui，Zou Jie-hui，Chen Shui-jin，et al. Calculation model of semiconductor thermoelectric generator unit based on variable material properties ［J］. Journal of South China University of Technology:Natural Science Edition，2013，41(4):47-53.

［11］Wang N，Wang C H，Lei J X，et al. Numerical study on thermal management of LED packaging by using thermoelectric cooling［C］∥Proceedings of International Conference on Electronic Packaging Technology ＆ High Density Packaging. ［S.l.］:IEEE，2009:433-437.

［12］Labudovic M，Li J. Modeling of TE cooling of pump lasers［J］.IEEE Transactions on Components and Packaging Technologies，2004，27(4):724-730.

［13］Zhang H Y，Mui Y C，Tarin M. Analysis of thermoelectric cooler performance for high power electronic packages［J］. Applied Thermal Engineering，2010，30(6):561-568.

［14］Ferrotec thermoelectric modules-peltier cooler model 9500/017/085B［EB/OL］［201-03-12］. https:∥thermal. ferrotec.com/index.php?id=module_detail＆mod_id=73.