链状卡塔型苯图的反强迫数
蒋晓艳
链状卡塔型苯图的反强迫数
蒋晓艳
(惠州学院 数学系,广东 惠州 516007)
设是一个有完美匹配的图. 若的边集满足有唯一完美匹配,则称为反强迫集. 包含边数最少的反强迫集叫做极小反强迫集,其边的数目叫做图的反强迫数. Damir Vukiěević等曾给出链状卡塔型苯图的反强迫数,但我们发现该结论存在问题,本文修正了并完善了链状卡塔型苯图的反强迫数.
链状卡塔型苯图;完美匹配;反强迫数
图的反强迫数的概念最初是2007年由Vukiěević等[1]在处理有缺陷的苯类化合物的过程中提出的,图的反强迫集可以看作是图删去(破坏)一些边后仅有的凯库勒结构. 文献[1]给出的反强迫数为1,其中是含有个六边形的苯型平行四边形,它共有行,每行有个六边形. 本人研究了硼氮富勒烯图的反强迫数[2].
1 链状卡塔型苯图的反强迫数
苯图是平面上连通的、由一系列全等的正则六角形按照任两个相邻六角形恰有一条公共边的方式堆砌而成的. 苯图是简单的平面二部图,苯图上无界面边界上的点称为外点,其他点(若存在)称为内点. 没有内点的苯图称为卡塔型苯图. 每个六角形至多与两个六角形相邻的卡塔型苯图称为链状卡塔型苯图,它又可分为线性的和扭结的两类,图1给出含5个扭结的链状卡塔型苯图. 定义连结两个相邻六角形中心的线段的长度为一个单元,记一个扭结中包含单元的数目为其长度,则图1中从左往右扭结的长度分别为2、1、1、1、3. 每个扭结的长度都是1的链状卡塔型苯图称为zigzag型苯图.
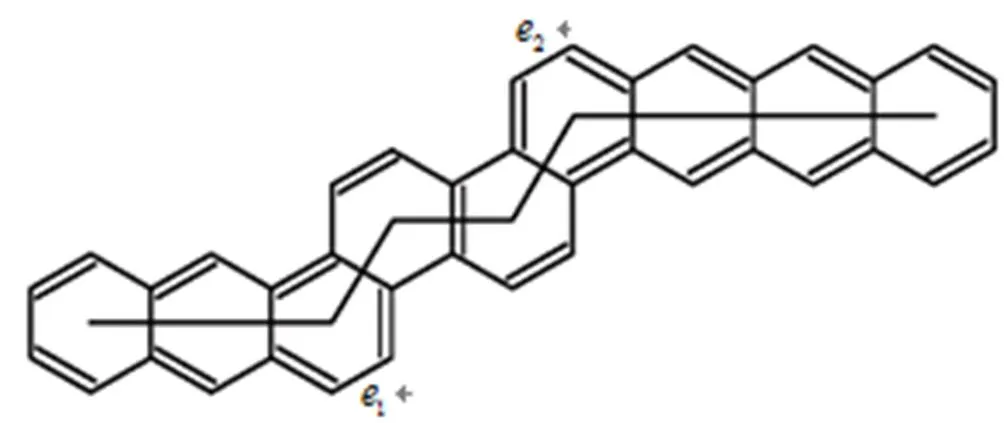
图1为5的链状卡塔型苯图以及其扭结的长度和反强迫数
定理1是Damir Vukiěević等给出的链状卡塔型苯图的反强迫数.
定理1[3]设是有个扭结的链状卡塔型苯图,则.
我们发现,在此条件下结论是不成立的,例如我们很容易看出图1中集合是苯图的一个大小为2的反强迫数,且此链状卡塔型苯图有5个扭结;但是,根据定理1,该图的反强迫数应为,矛盾. 下面我们给定理1添加一定的条件以得到正确结论.
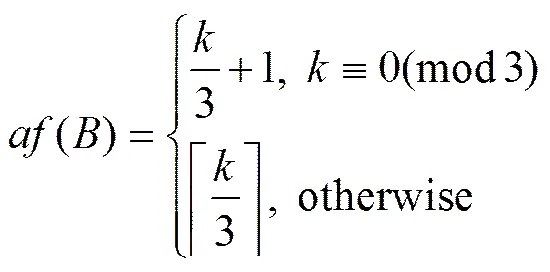

图2为1,2,3的链状卡塔型苯图的最小强迫集示意图
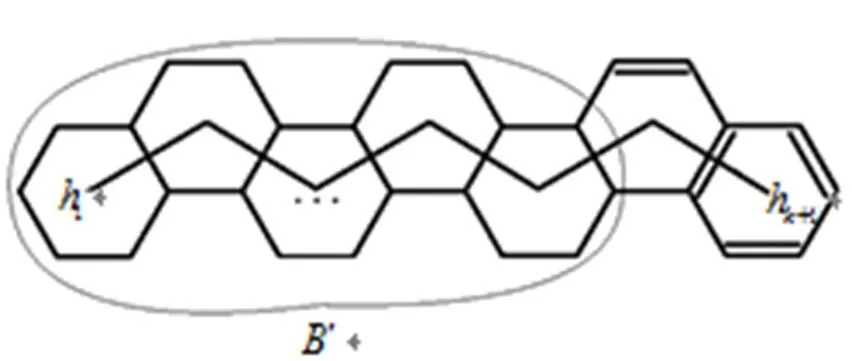
图3 情况1的证明示意图

图4 情况2的证明示意图
综上,定理3得证.
结合定理2和定理3可以得到定理4和定理5.

图5 反强迫数为的图的构造与证明
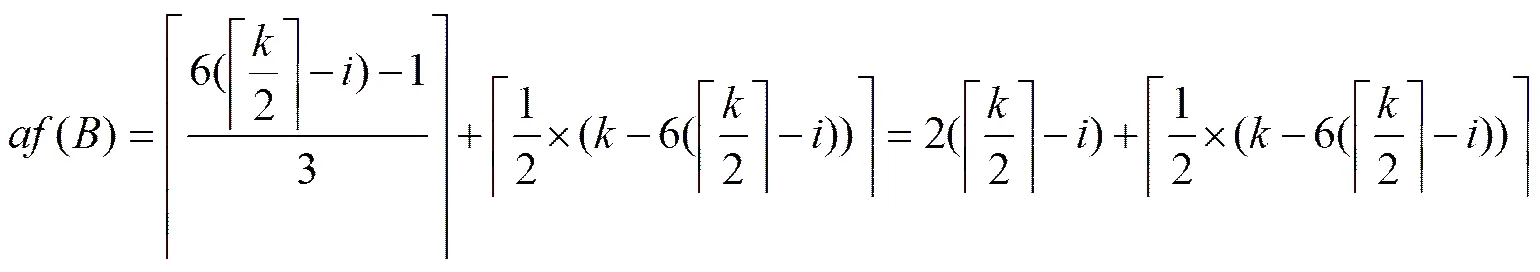

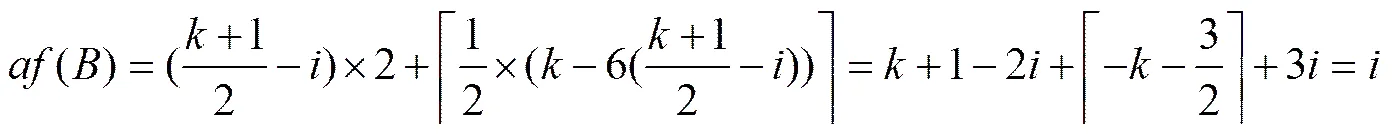
定理证毕.
[1] VUKIEEVIC D, TRINAJSTIC N. On the anti-forcing number of benzenoids [J]. J Math Chem, 2007, 42: 575-582.
[2] 蒋晓艳,程晓胜. 硼氮富勒烯图的反强迫数[J]. 湖北师范学院学报(自然科学版),2013, 33(3): 28-30.
[3] VUKIEEVIC D, TRINAJSTIC N. On the anti-Kekule number and anti-forcing number of cata-condensed benzenoids [J]. J Math Chem, 2008, 43: 719-726.
[责任编辑:熊玉涛]
The Anti-forcing Number of Chain Cata-condensed Benzenoids
JIANGXiao-yan
(Department of Mathematics, Huizhou University, Huizhou 516007, China)
Letbe a graph that admits a perfect matching. An anti-forcing set ofis the edge setsuch thathas a unique perfect matching. The anti-forcing set of the smallest cardinality is called the minimal anti-forcing set, and its cardinality is the anti-forcing numberof. Damir and Trinajatic gave an anti-forcing number of chain cata-condensed benzenoids, but we find the conclusion has some faults. In this paper, we correct the result and consummate the anti-forcing number of cata-condensed benzenoids.
cata-condensed benzenoids; perfect matching; anti-forcing number
1006-7302(2015)03-0001-04
O157.5
A
2014-12-23
国家自然科学基金资助项目(11226286);惠州学院博士启动基金资助项目().
蒋晓艳(1982—),女,山东青岛人,讲师,博士,研究方向为应用数学.

