基于修正Tail-VaR模型的我国财险公司经济资本测度

郑 慧，高 干，高天琪

（中国海洋大学，山东青岛 266100）

0 引言

经济资本需求量与保险公司面临的风险正相关，一定置信水平上的经济资本数量全面客观地反映了保险公司的整体风险，如何根据保险公司的自身经营特点和经营管理确定较为合理的一个资本水平，成为我国保险业亟待解决的重要课题。目前理论界和实务界有许多关于经济资本度量的方法，如违约损失率、VaR模型等，但多数不满足风险度量一致性原则,并且在风险损失分布拟合时多采用正态分布，未考虑风险损失分布厚尾特征[1]。基于此，本文以构建满足风险度量一致性条件下非正态分布的经济资本度量模型为目标，在Harry Panjer提出的Tail-VaR模型基础上[2]，尝试建立财险公司经济资本测度的修正Tail-VaR模型，以期为保险市场的运营及监督提供依据。

1 修正Tail-VaR理论模型构建

经济资本度量是将企业的风险损失这一随机变量转化成某一置信区间确定值的过程，其本质上是一种风险度量应用。由于传统的风险度量方法不满足风险度量一致性原则，Artzner提出满足风险度量一致性原则的风险度量函数Tail-VaR[3]，公式如下：

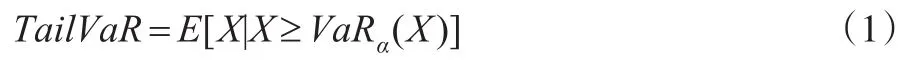
根据上式可知，X≥VaRα(X)的概率为（1-α）,故通过积分我们可以求出随机变量X在（1-α)概率下在VaR以上的数学期望值,并将其除以概率（1-α)可以得出X在整个范围内的Tail-VaR。

若VaRα(X)是连续函数，则TailVaR用积分表示公式如下：

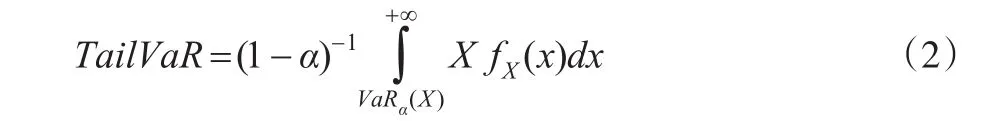
其中 fX(x)是随机变量X的分布密度。

传统的Tail-VaR模型总是假定损失率服从正态分布，正态分布的假定可以应用其特殊性将其转化为标准正态分布从而简化计算。然而由于金融数据的特殊性，往往存在厚尾特征，在很多情况下，正态分布不能很好的对金融数据进行拟合。因此需要对模型的分布进行修正，分析在其他重要分布下的Tail-VaR计算。在此，本文选择在标准正态分布、伽马分布和t分布三种假设，讨论Tail-VaR的修正模型构建问题。

1.1 基于正态分布的Tail-VaR分布修正

给定均值为μ,标准差为σ的正态分布，则其Tail-VaR计算公式为：

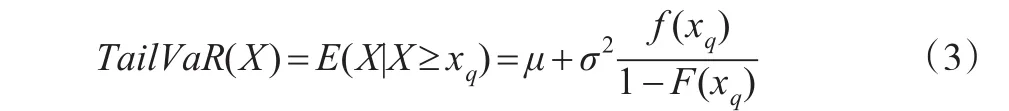
其中，f(xq)为正态分布的概率密度函数，F(xq)为正态分布的累积分布函数，xq为X在(1-q)时的分位数。我们知道任意正态分布都可以转化为标准正态分布，所以对于损失率服从正态分布的Tail-VaR值可以借助于标准正态分布进行计算，计算公式如下：

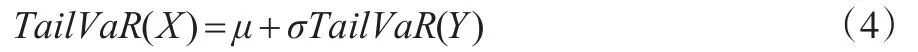
其中Y服从标准正态分布,即：

不同破产概率下的标准正态分布的VaR与Tail-VaR值如表1所示。由公式（4）可得正态分布下的Tail-VaR值。

1.2 基于伽马分布的Tail-VaR分布修正

在选用伽马分布时，不再具有正态分布的简化计算方法，由定义式推导可得Tail-VaR计算公式如下：

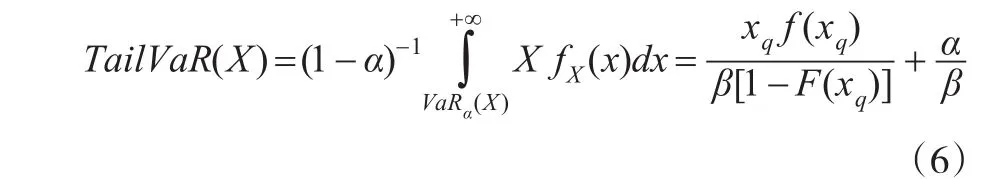
其中，f(xq)是伽马分布的密度函数，F(xq)为伽马分布的累积分布函数。

1.3 基于t分布的Tail-VaR分布修正

同上，对于t分布也只能通过定义式计算，其Tail-VaR计算公式如下：

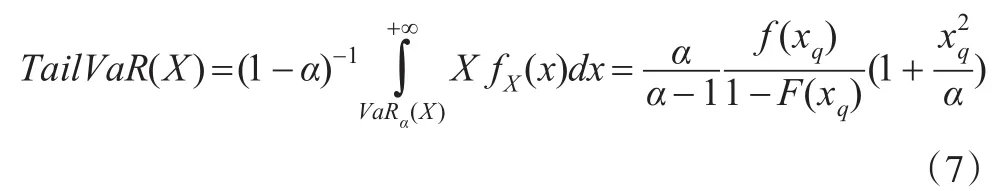
其中，f(x)是t分布的密度函数，F(x)为t分布的累积分布函数。

2 实证

2.1 样本选取与数据来源

从数据来源方面看，由于我国的财险业发展时间较短，相关的财务报表数据并不十分完善，因此本文选取了人民财产保险公司、大地财产保险公司等10家比较有影响力的财险公司，以2002～2011年《中国保险年鉴》相关统计数据为依据进行分析和计算。

为了消除资产规模对经济资本数量的影响，使用资产收益率（ROA）作为分析指标，ROA即净利润同总资产的比值。考虑到我国财险公司每年的资产数量变动比较大，可能对ROA产生影响，故对近两年的总资产取平均值。具体计算公式如下：

通过计算可得到我国财险公司的ROA描述性统计，具体结果见表2。

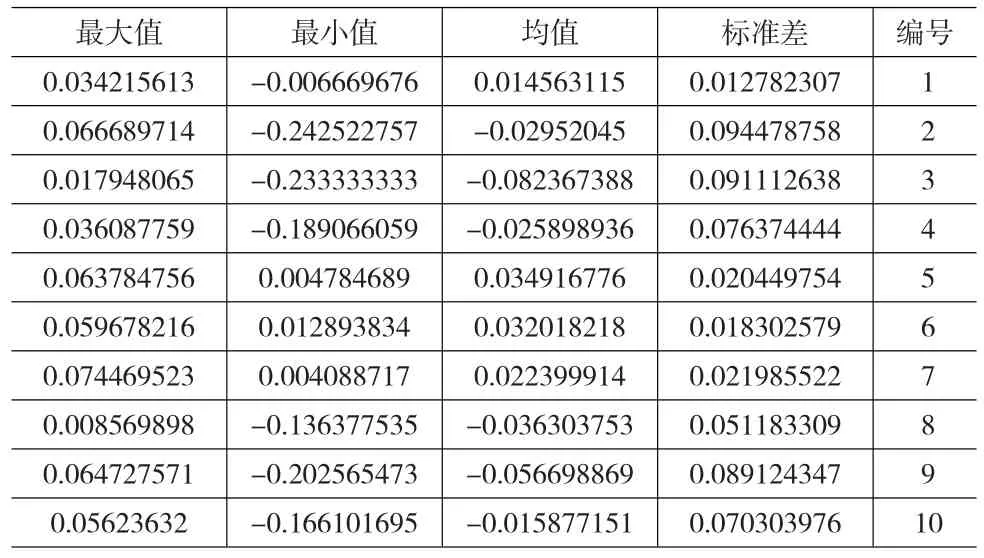
表2 我国财险公司ROA描述性统计

2.2 损失率分布假定

考虑到收益与风险损失的内在关系，使用ROA近似替代损失率。假设损失率为相应的ROA取负值。除此，假设损失率优先服从于正态分布，在显著不服从于正态分布的情况下，损失率服从于具有厚尾特征的伽马分布或者t分布，具体分布以实际的拟合情况为准。

（1）基于正态分布的损失率分布假定。

根据上文的基本假设可知，要验证损失率的正态分布特征可以通过验证ROA的正态分布特征来实现。由于可供分析的财务数据比较少，并且考虑到损失分布的厚尾特征，故本文选取显著性水平为0.1。也就是说若P值小于0.1拒绝原假设，即认为该财险公司的损失率不服从于正态分布。对数据的K-S检验与t检验结果见表4、表5。

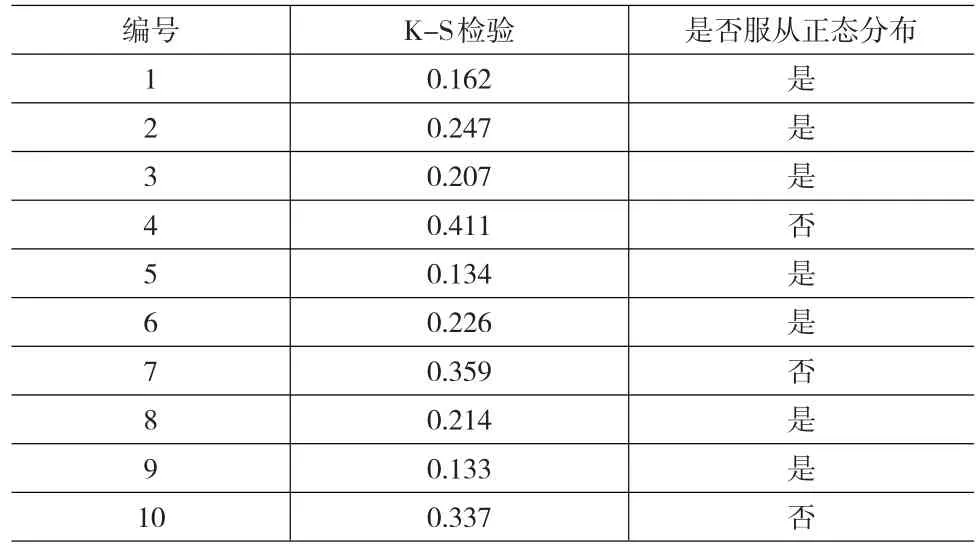
表4 K-S正态性检验结果

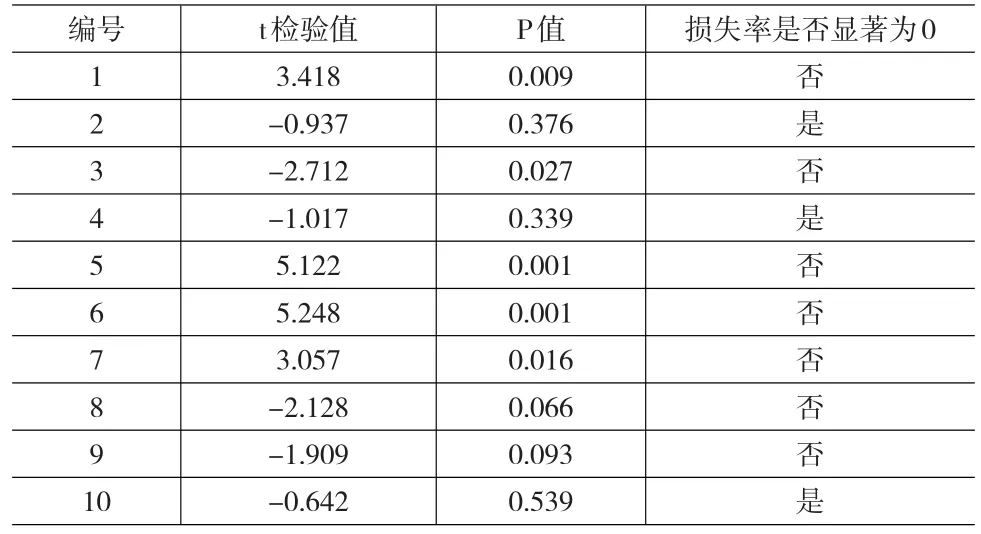
表5 单样本t检验结果

对表4、5结果进行分析，K-S正态性检验结果显示编号为1、2、3、5、6、8、9的财险公司损失率不能拒绝原假设，可认为其服从正态分布；编号为4、7、10的财险公司其损失率没有通过正态性检验。t检验结果显示编号2、4、10的财险公司损失率显著为0。

（2）基于伽马分布的损失率分布假定。

对于损失率未通过正态性检验的编号为4、7、10的财险公司，我们进一步分析其损失率所服从的分布。基于伽马分布的假定，结合概率分布直方图，进行参数估计，可得到编号为7的财险公司的损失率近似服从于伽马分布G(0.014，1.634)。其参数估计结果见表6。

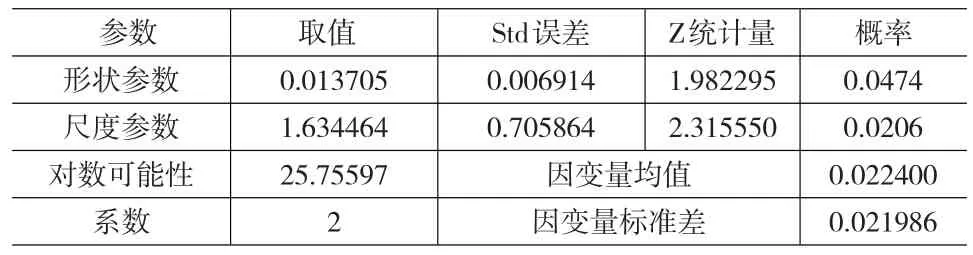
表6 伽马分布的参数估计结果

（3）基于t分布的损失率分布假定。

对于编号为4、10的财险公司，结合概率分布直方图，其损失率未通过t检验，其损失率均值显著为零，这也符合t分布的基本特征。其中，编号为4的财险公司的损失率近似服从于t分布t(2.241),编号为10的财险公司的损失率近似服从于t分布t(2.611)。

2.3 财险公司修正Tail-VaR经济资本计算

本文将财险公司的净利润(或净损失)视为随机变量，由此求得总资本的Tail-VaR就是为弥补风险损失我国财险公司所应准备的经济资本数量。

根据上文对正态分布、伽马分布和t分布下Tail-VaR的计算方法和公式的介绍，可以得出损失率基于不同分布下的我国财险公司的经济资本数量。

对于编号为1、2、3、5、6、8、9的财险公司，由于其损失率通过了正态性检验，我们采用基于正态分布的Tail-VaR模型运用代数方法进行经济资本计算。由于编号为2的财险公司的损失率未能通过t检验，我们假设其损失率服从于均值为0，标准差为0.0945的正态分布。结合表1的数据，应用公式（4）对正态分布下的不同置信水平的Tail-VaR进行计算，具体结果见表7。

由表7我们可以看到，同一置信水平下，损失率服从正态分布的各财险公司的Tail-VaR值不同；各财险公司不同置信水平下的Tail-VaR值也不同。

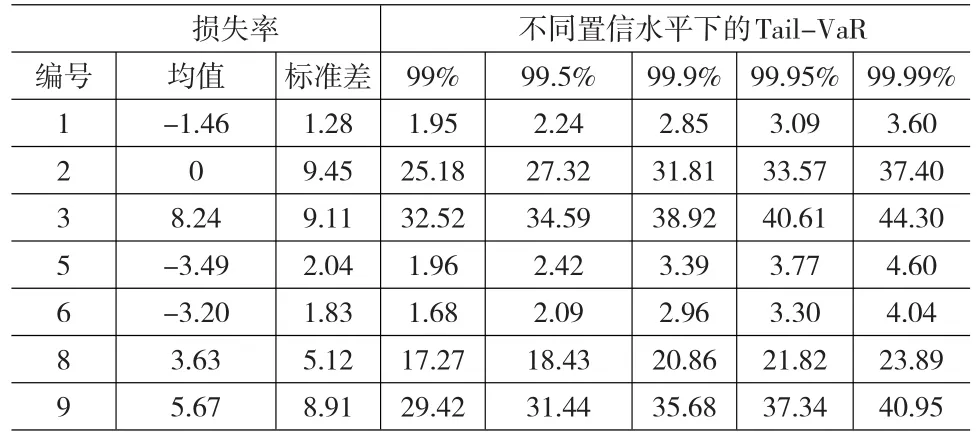
表7 正态分布下的Tail-VaR （单位：%）

考虑到保险公司面临较高的风险暴露，本文选取了99.9%的置信水平，以期保证保险公司在较大程度上应对非预期损失，利用2010年和2011年各财险公司的平均资产，估算各财险公司所需的的总体经济资本数量。具体结果见表8。

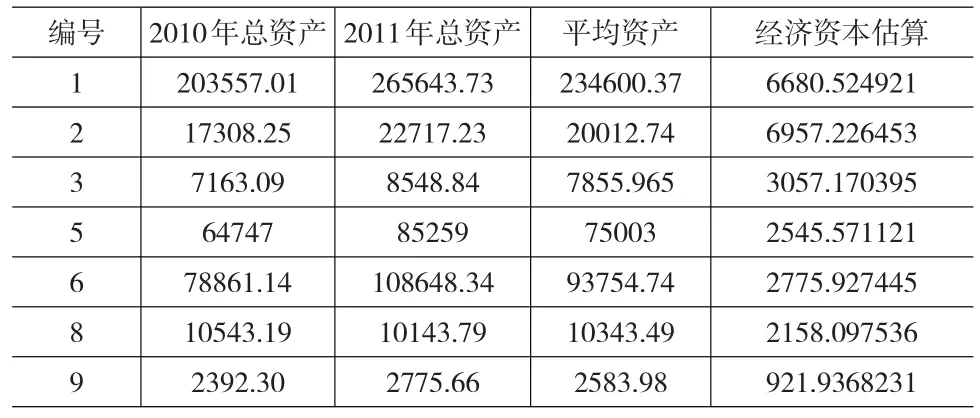
表8 2011年度各财险公司经济资本估算 （单位：百万元）

对于编号为4、7、10的财险公司由于其未通过正态性检验，只能采用前文提到的基于损失率非正态性的方法进行经济资本计算。对于编号为7的财险公司，由基于伽马分布的参数估计可知其损失率近似服从于G(0.014,1.634)，即α=0.014，β=1.634。使用逆伽马分布累计函数GAMMAINV(Probability,α,β)估计伽马分布的在 1%、0.5%、0.1%、0.05%、0.01%水平下的上分位点，求得xq。将xq代入伽马分布的概率密度函数中可以求得相应的f(xq)。同时可以求得相应的F(xq)。最后，将求得的α，β，xq，f(xq),F(xq)代入公式（6）求得基于伽马分布的不同置信水平下的TailVaR值。

对于编号为4、10的财险公司，测算方法与编号为7的财险公司类似。我们由基于t分布的参数估计可知编号为4的财险公司的损失率近似服从于t(2.241),编号为10的财险公司的损失率近似服从于t(2.611)。即对于编号为4、10的财险公司损失率，参数α分别等于2.241、2.611。两者计算方法相同，这里以编号为4的财险公司为例对不同置信水平下的Tail-VaR进行计算。首先使用分布累计函数估计t分布的在1%、0.5%、0.1%、0.05%、0.01%水平下的上分位点，求得xq。将xq代入t分布的概率密度函数中可以求得相应的f(xq)。同时可以求得相应的F(xq)。最后，将求得的α，xq，f(xq),F(xq)代入公式（7）求得基于t分布的不同置信水平下的Tail-VaR值。同样选取99.9%的置信水平，利用2010年和2011年各财险公司的平均资产，估算各财险公司所需的的总体经济资本数量。具体结果见表9。

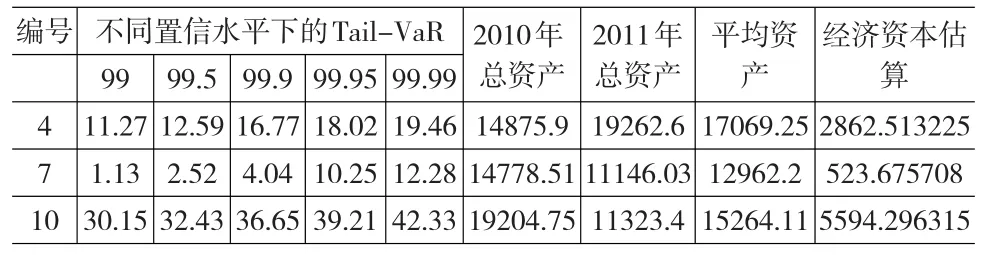
表9 2011年中国财险公司经济资本估算

其中，置信水平、Tail-VaR单位为%，总资产、平均资产、经济资本单位为百万元。

3 结论及启示

本文选取了我国10家财险公司，基于上文介绍的修正分布的Tail-VaR模型对其经济资本数量进行估算。观察各财险公司的TailVaR数值不难发现，风险状况较好的财险公司编号为1、5、6、7，风险状况处于中等水平的保险公司编号为4、8，剩余财险公司面临较大的风险冲击，必须重视其经营风险，防范意外损失。其中编号为3的财险公司的经济资本占比高达38.92%。对此，本文认为可以从以下几方面进行解释：经济资本测度的样本期间相对较短，可能会造成一定的测度偏差。但是仅从标准差也可以看出编号为3的财险公司损失率波动较大，风险控制应成为其日常经营管理的重要方面。最终通过10家财险公司的经济资本测算结果可以看出，我国保险行业存在的风险差异十分明显，且绝大多数的财险公司面临较为严重的风险暴露。对于保险公司积极应对风险、主动出击，经济资本的度量与控制不失为一个较为理想的工具。

为此，本文认为保险业的经营，首先要树立经济资本管理理念。在重视信用评级技术方法研究的同时，正确处理外部征信与内部评级的关系，借助和谐发展的信用评级环境，为保险业经济资本管理提供适宜的发展空间。另外，在进行经济资本度量与控制时不难发现，样本数据的完整性与准确性是制约风险管理效果的重要一环。要获得可靠、充分的数据支撑，历史资料积累是一方面，另一方面各保险公司以及其他金融机构的相互配合沟通也十分重要，一个有效的公共数据库的建立，将能够促使真正意义上经济资本管理效果的实现。当然，上述过程离不开监管部分的配合与鼓励。良好的政策支撑与法律保障，可以引导保险业经济资本管理向着积极方向发展，在合理进行风险管理的同时，为行业健康发展保驾护航。

[1]王稳,郭祥.基于TailVaR的我国保险公司经济资本度量研究[J].中国软科学,2012.

[2]Harry H P.Measurement of Risk，Solvency Requirements and Allocation of Capital Within Financial Conglomerates[R].AFIR/ICA Conference in Cancun in Mexico，2002(3).

[3]Artzner P，Delbaen F，Eber J M ，et al.Coherent Measures of Risk[J].Mathematical Finance ，1999，(3).