考虑启动压力梯度的弹性采收率计算方法及影响因素

张晓亮，杨仁锋，李　娜，2

（1.中海油研究总院，北京100028；2.海洋石油高效开发国家重点实验室，北京100028）

考虑启动压力梯度的弹性采收率计算方法及影响因素

张晓亮1，杨仁锋1，李娜1，2

（1.中海油研究总院，北京100028；2.海洋石油高效开发国家重点实验室，北京100028）

低渗透油藏流体渗流存在启动压力梯度，应用非达西渗流理论，对不同渗流形态下考虑启动压力梯度的弹性采收率计算方法进行了分析，给出了考虑启动压力梯度的直井、直井压裂、水平井和水平井压裂4种开发方式的弹性采收率计算公式，并通过实例分析不同参数对弹性采收率的影响。研究结果表明：随着启动压力梯度的增加，4种开发方式的弹性采收率均呈线性下降，其中直井降幅最大，水平井次之，水平井压裂降幅最小；4种开发方式的弹性采收率和单位压差弹性采收率均随压差的增加而增加，前者呈线性增加，后者增幅逐渐变缓；直井压裂开发的弹性采收率随压裂裂缝半缝长的增加而增加，但增幅逐渐变缓；对于水平井压裂开发，压裂裂缝半缝长较裂缝间距对弹性采收率的影响更大，且存在最优的压裂裂缝半缝长；对于启动压力梯度较大且弹性开发的低渗透油藏，宜采用压裂的方式来提高弹性采收率。

非线性渗流启动压力梯度渗流场弹性采收率计算方法影响因素

对于异常高压低渗透油藏或注水能力差的特低、超低渗透油藏，一般采用弹性能量开发。计算弹性采收率一般采用未饱和油藏封闭型驱动的物质平衡方法，未考虑低渗透油藏渗流的特殊性。目前在低渗透油藏渗流机理及开发技术等方面开展了大量研究［1-5］，但对弹性采收率计算方法的研究较少。在低渗透油藏中，原油的基本渗流规律不符合经典的达西定律。只有当压力梯度大于启动压力梯度时，流体才会发生流动［6-12］。启动压力梯度的存在，直接影响弹性开发结束后的地层压力分布，进而影响弹性采收率。笔者应用非达西渗流理论，提出了不同渗流形态下考虑启动压力梯度的弹性采收率计算方法，给出了考虑启动压力梯度的直井、直井压裂、水平井和水平井压裂4种开发方式的弹性采收率计算公式，并通过实例分析了不同参数对弹性采收率的影响，以期为低渗透油藏弹性开发设计提供依据。

1　计算原理

弹性采收率的常规计算公式为

式（1）仅适用于弹性开发结束后地层内各点压力由原始地层压力降至井底流压的情况，对于低渗透油藏，由于启动压力梯度的存在，弹性开发结束后地层中各点压力不同，应满足驱替压力梯度与启动压力梯度相等。因此，极限泄油范围内任一点处的地层压力为

令式（2）中 p=pi，可得。实际泄油半径小于等于极限泄油半径，故实际泄油半径可取井距之半或单井等效泄油面积对应的半径。

考虑启动压力梯度后，实际泄油范围内任一点处的压降为（Δp-Gr），因此，需求得平均地层压降并对常规计算公式中的Δp进行修正，才能获得低渗透油藏真实的弹性采收率［14-15］，其表达式为

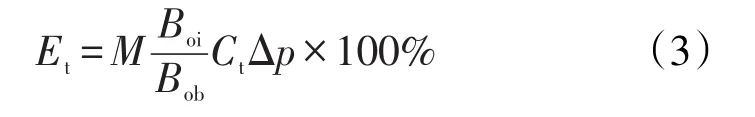
其中

2　单相渗流压差校正系数

根据经典渗流理论，渗流形态主要包括平面平行流、平面径向流和球面向心流3种。

2.1平面平行流

假设低渗透油藏一端为供给边缘，另一端为生产井，地层流体从供给边缘向生产井的渗流为平面平行流。这种情况下，弹性开发结束后平均地层压力为

根据压差校正系数的定义，可得

将式（5）代入式（6），可得平面平行流动状态下的压差校正系数为

当rw可忽略时，平面平行流动状态下的压差校正系数为

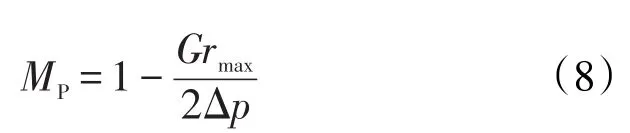
2.2平面径向流

假设1口直井位于低渗透油藏中心，当地层流体由供给边缘径向地流向井中时，此时渗流为平面径向流，弹性开发结束后平均地层压力为

结合式（6），可得平面径向流动状态下的压差校正系数为

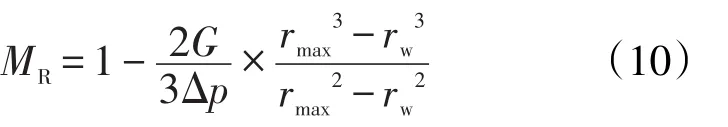
当rw可忽略时，平面径向流动状态下的压差校正系数为

2.3球面向心流

假设厚油层中部有一点汇，弹性开发结束后平均地层压力为

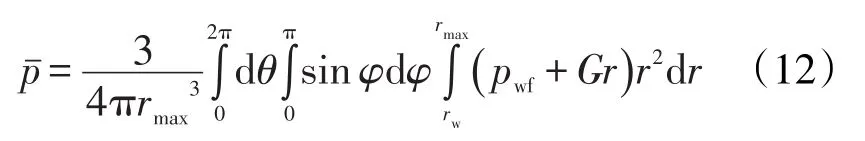
结合式（6），可得球面向心流动状态下的压差校正系数为

当rw可忽略时，球面向心流动状态下的压差校正系数为

从式（8）、式（11）和式（14）可以看出：①因Grmax≤Δp，考虑启动压力梯度后，压差校正系数小于1，说明启动压力梯度的存在降低了弹性采收率；②在泄油半径相同的条件下，MP＞MR＞MB，即平面平行流下可以获得更高的弹性采收率。

3　弹性采收率计算方法

低渗透油藏实际开发时渗流形态可划分为平面平行流、平面径向流和球面向心流3种基本渗流形态间的组合。只要求得不同渗流形态下对应的压差校正系数，总的压差校正系数可通过加权平均计算得到，其计算式为

将式（15）的计算结果代入式（3），即可得到考虑启动压力梯度的弹性采收率。

3.1直井与直井压裂

假设1口直井位于供给半径为re的圆形油藏中心，则渗流形态为平面径向流，由式（3）和式（11）可得

其中

对于直井压裂开发，假设压裂产生半缝长为L/2的垂直裂缝，则渗流形态包括平面平行流和平面径向流（图1）。

图1　直井压裂开发渗流场模型Fig.1　Modelsof flow field for the fractured verticalwell

对于平面平行流，由式（8）可得该状态下的压差校正系数为

对应的渗流体积为

对于平面径向流，由式（11）可得该状态下的压差校正系数为

对应的渗流体积为

联合式（3）、式（15）、式（18）—式（21），可得直井压裂开发的弹性采收率为

3.2水平井与水平井压裂

假设1口水平井位于供给半径为re、厚度为h的圆形油藏的中心，水平井段位于油层中部，长度为Lh，地层流体向井流动可以分解为：①近井区域的平面径向流和球面向心流（图2a）；②远井区域的平面径向流和平面平行流［16］（图2b）。

图2　水平井开发渗流场模型Fig.2　Modelsof flow field for thehorizontalwell

对于近井区域的平面径向流，由式（11）可得该状态下的压差校正系数为

对应的渗流体积为

对于近井区域的球面向心流，由式（14）可得该状态下的压差校正系数为

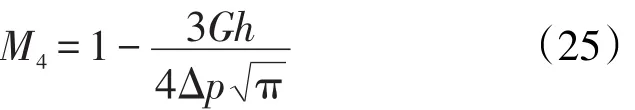
对应的渗流体积为

对于远井区域的平面径向流，由式（10）可得该状态下的压差校正系数为

对应的渗流体积为

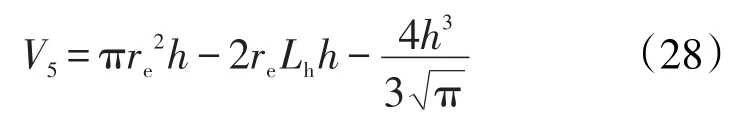
对于远井区域的平面平行流，由式（7）可得该状态下的压差校正系数为

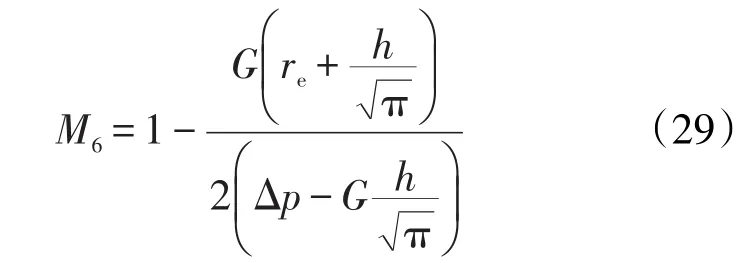
对应的渗流体积为

联合式（3）、式（15）、式（23）—式（30），可得水平井开发的弹性采收率为

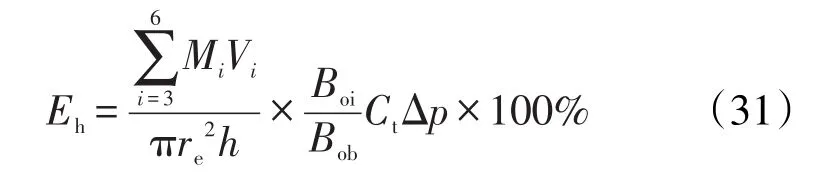
若忽略近井区域的球面向心渗流，可将渗流形态简化为平面平行流和平面径向流，则水平井开发的弹性采收率可用式（22）计算，其中裂缝长度取水平井段长度。

水平井多采用多段压裂以提高开发效果［17］，对于压裂水平井，假设在水平井段上均匀分布n个裂缝，渗流形态可简化为3个平面平行流（图3）。

对于垂直裂缝间的渗流，由式（8）可得平面径向流状态下的压差校正系数为

图3　水平井压裂开发渗流场模型Fig.3　Modelsof flow field for the fractured horizontalwell

对应的渗流体积为

对于平行井间的渗流，由式（8）可得平面径向流状态下的压差校正系数为

对应的渗流体积为

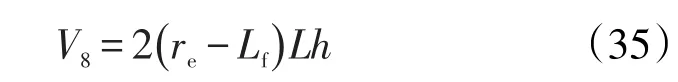
对于井两端的平行流，由式（8）可得平面径向流状态下的压差校正系数为

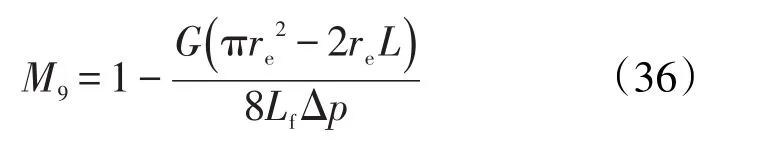
对应的渗流体积为

联合式（3）、式（15）、式（32）—式（37），可得水平井压裂开发的弹性采收率为

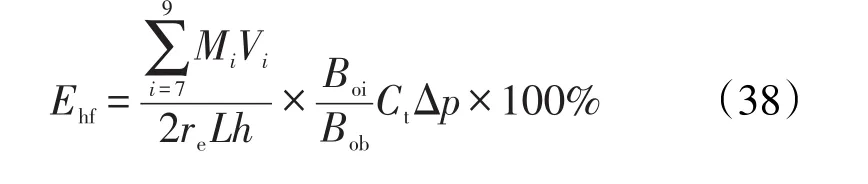
4　弹性采收率影响因素

A油藏位于准噶尔盆地腹部，油藏埋深为5 880 m，原始地层压力为97MPa，地层压力系数为1.69，平均气测渗透率为0.6×10-3μm2。属于异常高压特低渗透油藏，注水能力差，并且不具备注水条件，驱动类型主要为弹性驱动。

计算的参数包括：综合压缩系数为2.5×10-3MPa-1，原始地层压力为97 MPa，井底流压为47 MPa，原始压力下体积系数为1.3，饱和压力下体积系数为1.2，启动压力梯度为0.02MPa/m，供油半径为500m，油层厚度为20m；水平井段长度为300m；裂缝半缝长为50m，压裂段数为3。

利用新建方法计算了直井、直井压裂、水平井和水平井压裂4种开发方式的弹性采收率，并对其影响因素进行了分析。

4.1启动压力梯度

应用常规方法计算得到直井、直井压裂、水平井和水平井压裂4种开发方式的弹性采收率均为10.83%，考虑启动压力梯度后，在启动压力梯度相同的条件下，直井开发弹性采收率最低，水平井压裂开发弹性采收率最高；且随着启动压力梯度的增加，弹性采收率呈线性下降，其中直井降幅最大，水平井次之，水平井压裂降幅最小（图4）。因此，对于启动压力梯度较大且弹性开发的油藏，宜采用压裂的方式来提高弹性采收率。

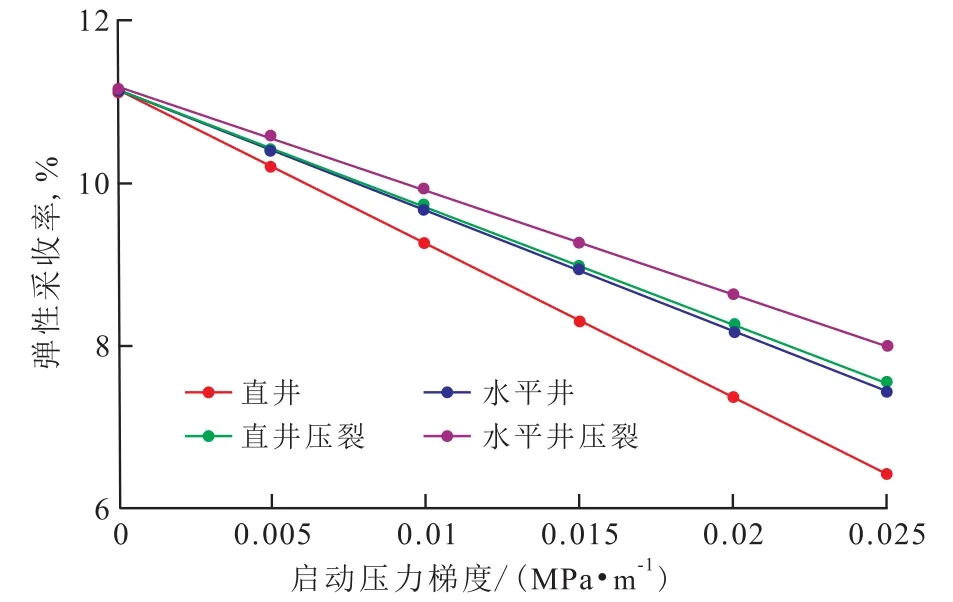
图4　启动压力梯度对弹性采收率的影响Fig.4　Effectof threshold pressure gradienton naturaldepletion oil recovery

由于算例中压裂直井的裂缝缝长等于水平井段长度，因此计算的弹性采收率具有可对比性，水平井因为考虑了近井区域的平面径向流和球面向心流，因此计算得到的水平井开发弹性采收率略低于直井压裂开发，当启动压力梯度为0.02MPa/m时，水平井压裂开发弹性采收率为8.01%，直井压裂开发弹性采收率为8.04%，这主要是因为启动压力梯度在近井区域贡献较小。当地层厚度和启动压力梯度均较小时，可忽略近井区域的球面向心流，计算水平井开发弹性采收率时可采用式（22）进行近似估计。

4.2压差

由图5可以看出：直井、直井压裂、水平井和水平井压裂4种开发方式的弹性采收率和单位压差弹性采收率均随压差的增加而增加，只是增幅不同，前者均呈线性增加，后者增幅均逐渐变缓。若不考虑启动压力梯度的影响，单位压差弹性采收率恒为0.54%/MPa，这说明在考虑启动压力梯度的情况下，随着压差的增大，能量利用率逐渐提高。

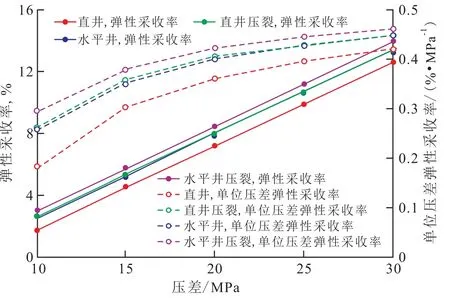
图5　压差对弹性采收率和单位压差弹性采收率的影响Fig.5　Effectofpressure drawdown on naturaldepletion oil recovery and thatperunitpressure drop

4.3压裂裂缝半缝长及间距

对于直井压裂开发，随着压裂裂缝半缝长的增加，弹性采收率增加，但增幅逐渐变缓（图6），存在最优的压裂裂缝半缝长，算例中最优压裂裂缝半缝长约为150～200m。

图6　压裂裂缝半缝长对弹性采收率的影响Fig.6　Effectofhalf fracture length on natural depletion oil recovery

图7　水平井压裂裂缝半缝长和裂缝间距对弹性采收率的影响Fig.7　Effectofhalf fracture length and fracture space on naturaldepletion oil recovery

对于水平井压裂开发，当水平井段长度为750m时，不同压裂裂缝半缝长及裂缝间距下的弹性采收率（图7）表明，随着压裂裂缝半缝长的增加或裂缝间距的缩短，弹性采收率均增加，但压裂裂缝半缝长影响更大，因此，对于水平井压裂开发应采用相对稀的“长裂缝”，而不是相对密的“短裂缝”。当裂缝间距小于150m时，弹性采收率增幅很小，因此从弹性采收率的角度，压裂裂缝间距以150m为宜。

5　结论

考虑启动压力梯度后，相同泄油半径下不同渗流形态的弹性采收率不同，平面平行流最大，球面向心流最小。压裂可将渗流形态由平面径向流变为平面平行流，其为提高弹性采收率的有效方式。

4种开发方式的弹性采收率随启动压力梯度的增大而降低，单位压差弹性采收率随压差的增大而增大，但增幅逐渐变缓。

考虑启动压力梯度后，对于直井压裂开发，弹性采收率随着压裂裂缝半缝长的增加而增加，且存在最优压裂裂缝半缝长；对于水平井压裂开发，压裂裂缝半缝长较裂缝间距对弹性采收率的影响更大，压裂裂缝间距以150m为宜。

符号解释：

Et——弹性采收率，%；Boi——原始地层压力下体积系数；Bob——饱和压力下体积系数；Ct——综合压缩系数，MPa-1；Δp——生产压差，MPa；p——地层压力，MPa；r——地层内任一点距井筒的距离，m；pwf——井底流压，MPa；G——启动压力梯度，MPa/m；rlim——极限泄油半径，m；pi——原始地层压力，MPa；M——压差校正系数；pˉ——平均地层压力，MPa；A——井筒至供给边缘距离，m；rmax——实际泄油半径，m；rw——油井半径，m；y——平面平行流状态下地层内任一点距井筒的垂直距离，m；x——平面平行流状态下地层内任一点距井筒的水平距离，m；Mp——平面平行流状态下的压差校正系数；θ——地层内任一点与水平方向的夹角，rad；MR——平面径向流状态下的压差校正系数；φ——地层内任一点与垂直方向的夹角，rad；MB——球面向心流状态下的压差校正系数；i——不同井型不同渗流形态下的序号；T——渗流形态总数；Mi——不同井型不同渗流形态下压差校正系数；Vi——不同井型不同渗流形态下对应的渗流体积，m3；Ev——直井开发的弹性采收率，%；S——单井泄油面积，m2；L——裂缝长度，m；h——地层厚度，m；Evf——直井压裂开发弹性采收率，%；Lh——水平井段长度，m；Eh——水平井开发弹性采收率，%；n——压裂级数；Lf——压裂裂缝半缝长，m；Ehf——水平井压裂开发的弹性采收率，%。

［1］ 李元生，李相方，藤赛男，等.低渗透气藏产水气井两相产能方程研究［J］.特种油气藏，2014，21（4）：97-100. Li Yuansheng，Li Xiangfang，Teng Sainan，etal.Research on twophase productivity equation forwater-producing gaswell in lowpermeability gas reservoir［J］.Special Oil&Gas Reservoirs，2014，21（4）：97-100.

［2］ 张江华，刘传虎，朱桂林，等.莫西庄油田低渗透储层特征与成因［J］.特种油气藏，2014，21（3）：58-61. Zhang Jianghua，Liu Chuanhu，Zhu Guilin，et al.Characteristics and genesis of low permeability reservoirs in the Moxizhuang oilfield［J］.SpecialOil&Gas Reservoirs，2014，21（3）：58-61.

［3］ 曲占庆，何利敏，窦小康，等.低渗透油藏水平井流入动态分析及举升方式优选［J］.油气地质与采收率，2013，20（6）：54-60. Qu Zhanqing，He Limin，Dou Xiaokang，et al.Inflow performance analysis and optimization of artificial lifting for horizontalwells in low permeability reservoir［J］.Petroleum Geology and Recovery Efficiency，2013，20（6）：54-60.

［4］ 王锋，刘慧卿，吕广忠.低渗透油藏长缝压裂直井稳态产能预测模型［J］.油气地质与采收率，2014，21（1）：84-86，91. Wang Feng，Liu Huiqing，LüGuangzhong.Steady-state productivity predictionmodel for long-length fractured verticalwell in low permeability oil reservoirs［J］.Petroleum Geology and Recovery Efficiency，2014，21（1）：84-86，91.

［5］ 徐亮.低渗透油藏差异开发技术研究与实践——以济阳坳陷博兴洼陷为例［J］.油气地质与采收率，2014，21（4）：107-110. Xu Liang.Research and practice of differencial development technologies in low permeability oil reservoirs：case study of Boxing sag，Jiyang depression［J］.Petroleum Geology and Recovery Efficiency，2014，21（4）：107-110.

［6］ 许建红，程林松，周颖，等.一种求解低渗透油藏启动压力梯度的新方法［J］.石油勘探与开发，2007，34（5）：594-597. Xu Jianhong，Cheng Linsong，Zhou Ying，et al.A new method for calculating kickoff pressure gradient in low permeability reservoirs［J］.Petroleum Exploration and Development，2007，34（5）：594-597.

［7］ 熊伟，雷群，刘先贵，等.低渗透油藏拟启动压力梯度［J］.石油勘探与开发，2009，36（2）：232-235. XiongWei，LeiQun，Liu Xiangui，etal.Pseudo threshold pressure gradient to flow for low permeability reservoirs［J］.Petroleum Exploration and Development，2009，36（2）：232-235.

［8］ 赵益忠，程远方，刘钰川，等.启动压力梯度对低渗透油藏微观渗流及开发动态的影响［J］.油气地质与采收率，2013，20（1）：67-69，73. Zhao Yizhong，Cheng Yuanfang，Liu Yuchuan，et al.Study on influence ofstart-up pressure gradient tomicro-seepage in low permeability reservoirs and development trends［J］.Petroleum Geology and Recovery Efficiency，2013，20（1）：67-69，73.

［9］ 田冷，顾永华，何顺利.低渗透油藏非线性渗流产能计算模型及参数敏感性分析［J］.水动力学研究与进展A辑，2011，26（1）：108-115. Tian Leng，Gu Yonghua，He Shunli.Study on the nonlinear radial stable flowmodel in the low permeable reservoir［J］.Chinese JournalofHydrodynamics，2011，26（1）：108-115.

［10］姜瑞忠，杨仁锋，马勇新，等.低渗透油藏非线性渗流理论及数值模拟方法［J］.水动力学研究与进展A辑，2011，26（4）：445-452. Jiang Ruizhong，Yang Renfeng，Ma Yongxin，etal.Nonlinear percolation theory and numerical simulation in low permeability reservoirs［J］.Chinese JournalofHydrodynamics，2011，26（4）：445-452.

［11］王晓冬，郝明强，韩永新.启动压力梯度的含义与应用［J］.石油学报，2013，34（1）：188-191. Wang Xiaodong，Hao Mingqiang，Han Yongxin.Implication of the threshold pressure gradient and its application［J］.Acta Petrolei Sinica，2013，34（1）：188-191.

［12］时佃海.低渗透砂岩油藏平面径向渗流流态分布［J］.石油勘探与开发，2006，33（4）：491-494. Shi Dianhai.Flow state distribution of areal radial flow in low permeability sandstone reservoir［J］.Petroleum Exploration and Development，2006，33（4）：491-494.

［13］陈光梅，车雄伟.弹性驱低渗透油气藏的分区物质平衡方法［J］.新疆石油地质，2011，32（2）：157-159. Chen Guangmei，Che Xiongwei.Domain material balancemethod for low permeability gas-oil reservoir by depletion drive process ［J］.Xinjiang Petroleum Geology，2011，32（2）：157-159.

［14］姜瑞忠，张晓亮.低渗透油藏弹性采收率计算方法研究［J］.特种油气藏，2008，15（4）：70-72. Jiang Ruizhong，Zhang Xiaoliang.Calculation method of natural depletion oil recovery of low-permeability reservoirs［J］.Special Oil&GasReservoirs，2008，15（4）：70-72.

［15］陈明强，张明禄，蒲春生，等.变形介质低渗透油藏水平井产能特征［J］.石油学报，2007，28（1）：107-110. Chen Mingqiang，Zhang Minglu，Pu Chunsheng，etal.Productivity ofhorizontalwell in deformationmedium of low-permeability reservoirs［J］.Acta PetroleiSinica，2007，28（1）：107-110.

［16］张学文，方宏长，裘怿楠，等.低渗透率油藏压裂水平井产能影响因素［J］.石油学报，1999，20（4）：51-55. Zhang Xuewen，Fang Hongchang，Qiu Yinan，etal.A study on factors affecting the performance of hydraulically fractured horizontal well in low permeability reservoirs［J］.Acta Petrolei Sinica，1999，20（4）：51-55.

［17］郝明强，胡永乐，李凡华.特低渗透油藏压裂水平井产量递减规律［J］.石油学报，2012，33（2）：269-273. HaoMingqiang，Hu Yongle，LiFanhua.Production decline laws of fractured horizontalwells in ultra-low permeability reservoirs［J］. Acta PetroleiSinica，2012，33（2）：269-273.

编辑常迎梅

Com putingmethod and influencing factorsof naturaldep letion oil recovery in consideration of threshold pressuregradient

Zhang Xiaoliang1，Yang Renfeng1，LiNa1，2

（1.CNOOCResearch Institute，Beijing City，100028，China；2.State Key Lab ofOffshoreOil Exploitation，Beijing City，100028，China）

There isa threshold pressure gradient in the flow of fluid in low-permeability reservoirs.Based on the non-Darcy flow theory，a new computingmethod ofnatural depletion oil recovery considering the threshold pressure gradient in different flow forms was analyzed.The calculating formulas for depletion oil recovery of the vertical well，fractured vertical well，horizontalwell，and fractured horizontalwell in the low-permeability reservoirwere developed.The effectof each parameter on the depletion oil recoverywas discussed while applying the formulas to real cases.The results show that the depletion oil recovery decreased linearlywith the increase of threshold pressure gradient.The oil recovery of the verticalwells is very sensitive to the threshold pressure gradient，the horizontalwell is less sensitive，and the effect for the fractured horizontalwells is theweakest.The depletion oil recovery and the one perunitpressure drawdown increaseswith pressure drawdown linearly and in a gradually slowermanner respectively.The depletion oil recovery of the fractured verticalwell increaseswith the half fracture length，but the effectdecreases gradually.Half fracture length ismore sensitive than fracture space to the depletion oil recovery in the fractured horizontalwells.There is optimized half fracture length.It is recommended that the low-permeability reservoirwith large threshold pressure gradientunder depletion developmentshould be developed with hydraulic fracturing.

non-linear flow；threshold pressure gradient；flow field；natural depletion oil recovery；computingmethod；influencing factors

TE313.7

A

1009-9603（2015）02-0072-06

2015-01-13。

张晓亮（1983—），男，内蒙古通辽人，工程师，硕士，从事油藏工程方法研究及应用。联系电话：（010）84526464，E-mail：zhangx l16@cnooc.com.cn。

国家科技重大专项“海上油田丛式井网整体加密及综合调整技术”（2011ZX05024-002）。