环境参数对运动人体热舒适性影响的理论模型与实验研究

季 泰，袁伟琪，李登峰，杨 剑，季 浏

1 引言

2013年8月11日晚，广州天河体育馆迎来了天王之战，万众瞩目的世界羽毛球锦标赛男子单打决赛在林丹和李宗伟之间决出，最终因李宗伟虚脱退赛林丹夺得冠军。尽管林丹不负众望，但李宗伟最后时刻退赛不免令人觉得些许遗憾。赛后，马来西亚男子单打教练员认为，正是因为决赛第2局时场馆空调突然关闭，场馆温度过高才导致李宗伟最后虚脱退赛，这引起了研究者对环境参数影响运动人体热舒适性的关注。

热舒适是人对周围热环境所做的主观满意度评价［13］。有关人体热舒性的研究从20世纪初逐步发展［4］，在20世纪60年代之前，多数研究只考虑环境因素中的某个或部分因素对人体热舒适性的影响，直到1962年，Macpherson提出6个热舒性基本评价因素，包括空气温度、流动速度、平均辐射温度、新陈代谢速率、相对湿度以及衣服热阻［15］，之后许多学者开始进行综合性的人体热舒适性研究。丹麦科技大学的Fanger基于人体热平衡方程建立了热舒适模型，提出了PMV-PPD（Predicted Mean Vote，Predicted Percentage of Dissatisfied）评价指标［11］；1994年，国际标准化组织在Fanger的基础上提出了ISO7730标准，详细规定了高舒适度室内环境要素和控制值［13］；Huizenga等人考虑了人体生理机能对热舒适的影响，建立了Berkeley模型［12］；美国供暖、制冷与空调工程师协会（ASHRAE）明确对热舒适提出定义，并且对影响舒适性的各种因素进行了详细说明［18］。

国内从20世纪80年代开始进行有关人体热舒适的研究。文学军等研究了动态环境下人体热感觉的评价方法，提出了动态环境中人体热感觉模糊综合评判方法［6］；周翔等针对PMV指标在动态环境下的情况做了研究，对动态环境下PMV值偏高做出了合理解释［9］；刘荣向等通过统计学分析软件SPSS和ORIGIN对数据进行分析，重点研究不同情况下人体新陈代谢率和皮肤温度两个指标对人体热感觉的影响［2］；邱曼等研究了不同温度、不同活动强度下人体出汗率与其他生理指标的变化，分析影响出汗的因素［5］；纪秀玲根据实验和现场调查结果分别提出了出汗状态下人体热感觉、热不舒适的数学预测模型，建立了人体出汗状态下服装潜热蒸发热阻计算模型［1］。

人体在体育运动时与安静状态下有着很大的差别，这是因为运动人体具备以下特点:1）新陈代谢速率大；2）衣着热阻小；3）排汗量大；4）辐射环境复杂。Fanger的热平衡方程是建立在常温、低活动水平条件下，在新陈代谢速率较高（大于4.0METs）或者高温情况下无法准确地反映人体的热感觉［2，7，17］。因此，传统的基于Fanger模型的人体舒适性研究指标难以准确预测运动时的热舒适情况，导致PMV指标偏向热感觉较高的一边，这就需要对原平衡方程进行修正。本研究通过对运动人体对流辐射模型以及体表扩散模型的修正，使热舒适评价模型更加合理，并通过实验对Fanger模型以及修正后的模型进行比较验证。

2 运动人体热舒适性模型

2.1 Fanger模 型［8，15］

Fanger基于人体热平衡方程提出了PMV-PPD评价方法，人体热平衡方程为:

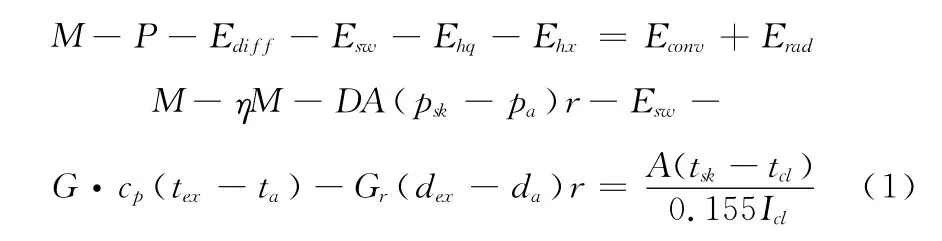
其中，M:人体代谢产热速率，W；P:人体对外做功功率，W；Ediff:体表扩散失热速率，W；Esw:汗液蒸发散热，W；Ehq:呼吸潜热失热，W；Ehx:呼吸显热失热，W；Econv:对流散热，W；Erad:辐射散热，W；η:人体对外做功系数；D:皮肤水蒸汽扩散系数，取0.081kg／（m2·h·Pa）；A:人体表面积，m2；psk:皮温下饱和水蒸汽压力，Pa；pa:周围空气水蒸汽分压力，Pa；r:气化潜热，取2409J／g；Gr:呼吸空气量，kg／h，经验值取 Gr＝0.005，16M；cp:空气比热，1.01J／（g·℃）；ta、da:周围空气温度和湿度，℃、%；tex、dex:呼出空气的温度和湿度，℃、%；tsk:皮肤温度，℃；tcl:人体服装外表面平均温度，℃；Icl:衣服热阻，clo。将所有项移至方程一边，令:

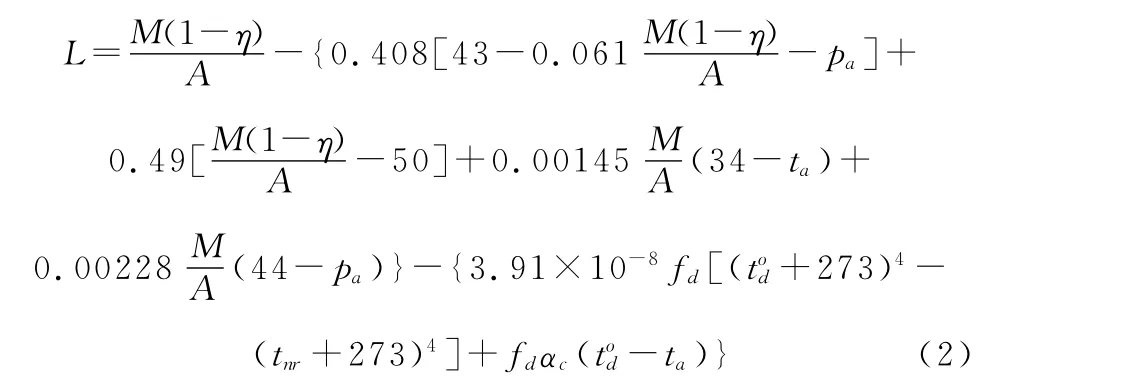
其中，fcl:服装表面积与对应着衣体表面积之比；αc:对流换热系数，W／（m2·℃）；tmr:环境周围表面平均温度，℃:人体外表面平均温度，℃；L为热负荷，表征人体单位时间内单位面积达到热平衡的散热速率的差距，L小于0时表示散热速率大于产热速率，大于0时则表示散热速率小于产热速率。Fanger利用Kansas州立大学对1396名受试者的资料，提出了如下关系式:

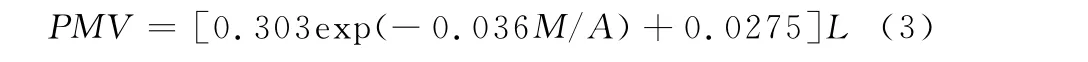
PMV（Predicted Mean Vote）是一个表征人体冷热感的评价指标，代表在同一环境下绝大多数人的舒适感觉，共有7级指标:

表1 PMV热感觉标尺一览表Table 1 The Standard of Thermal Sense

由于人与人之间的生理差别，PMV指标并不能完全准确地反映所有人的热舒适感觉，依旧会有少数人对大多数人感到满意的热中性条件表现出不满意，故提出PPD（Predicted Percentage of Dissatisfied）指标，表示人群对热环境不满意的百分数，PPD与PMV关系式为:

2.2 修正模型

本研究针对运动人体衣着少、出汗多、呼吸急促、辐射环境复杂的特点，参照最新研究成果，对Fanger模型中的部分项进行修改。

2.2.1 体表扩散失热

Fanger模型在皮肤温度的计算公式上，只体现了皮肤温度与新陈代谢的联系，即:

而实际上，皮肤温度是由人体核心至皮肤表面的热流与皮肤表面至环境散热之间的热平衡决定的［16］，应当将环境因素考虑进去，修改后的皮肤温度模型考虑了环境湿度、环境温度、环境风速（va，m／s）以及衣服热阻对运动人体热感觉的影响［14］，因此更加合理，即

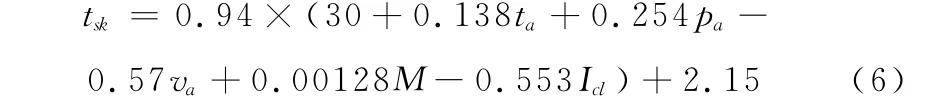
故扩散项为:

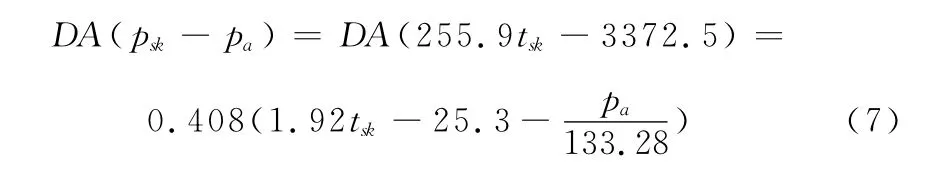
2.2.2 对流散热以及辐射换热

Fanger的模型中，在计算人体表面散热量时使用着衣人体平均温度tcl，在计算运动人体时因其较小的服装覆盖率而不够准确，且未考虑运动对于服装热阻的影响。新的模型将人体表面散热区域分为着衣体及非着衣体两部分，定义衣着覆盖率代表着衣表面占人体表面积的比率:

其中，Af:人体着衣部分面积m2；A:人体表面积。由于运动服多用针织面料制成，为简化计算，其单位热阻以0.2clo计算［3］。考虑到运动速度对衣服热阻的影响，运动时由于人体与空气间存在相对流速，会降低服装的热阻，其热阻值可用下式估算［9］:

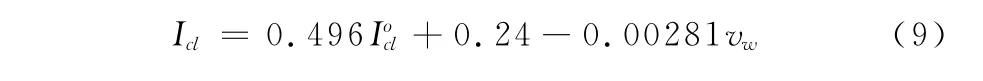
其中，Icl:衣服实际热阻，clo:衣服原热阻，clo辐射散热项修正为:

其中，μ:着衣体占人体表面积的比率；εy:服装表面发散率，取0.95；εf:人体表面发射率，取1；feff:有效辐射面积，取0.72；σ:玻尔兹曼常数，5.67×10-8W／（m2K4）

对流散热项修正为:

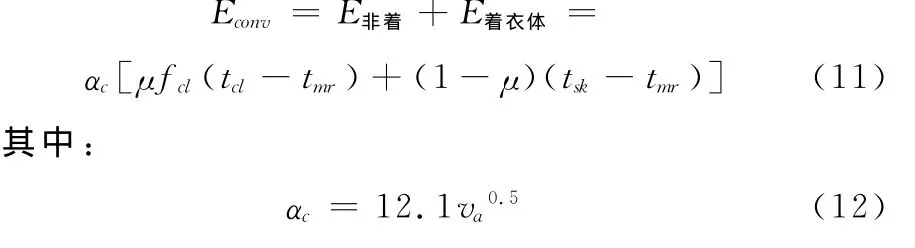
将修改后的公式（5）（8）（9）（10）代入式（1）得:

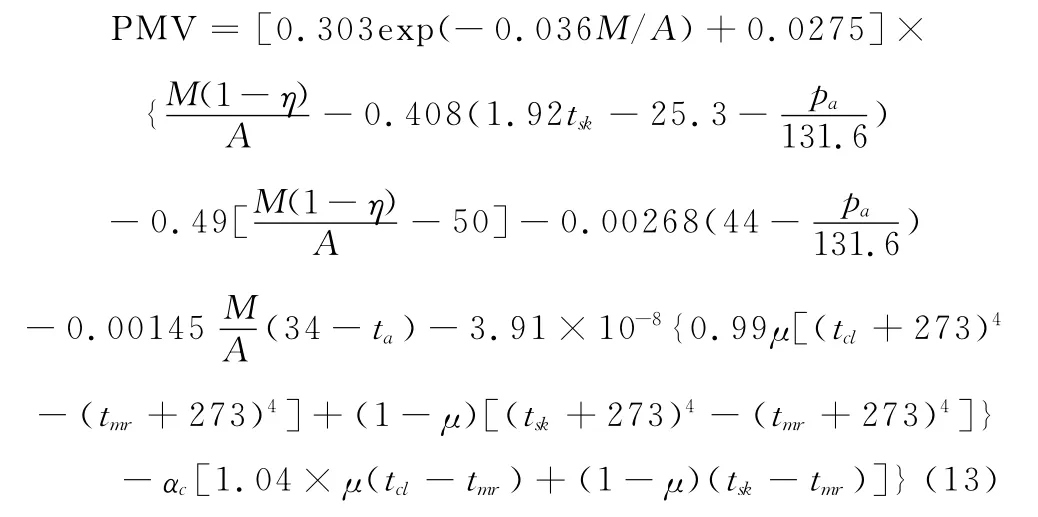
公式（13）即为修正后的运动人体热舒适模型计算公式。

3 模拟与对比

公式（3）为Fanger人体热舒适模型，公式（13）为修正后的运动人体热舒适模型，采用Fortran语言对两种模型进行编程计算与对比。假定某羽毛球运动员身高为180 cm，体重75kg，衣着为短袖衫短裤（按衣着覆盖率70%计算）进行比赛，参照参考文献［10］可知新陈代谢速率约为7METs。输入的数据处理:温度、风速等可以直接运用，输入的湿度为相对湿度z，则水蒸气分压pa＝zpab，其中，环境温度下饱和水蒸气压力pab由Goff Gratch公式的简化形式计算所得:

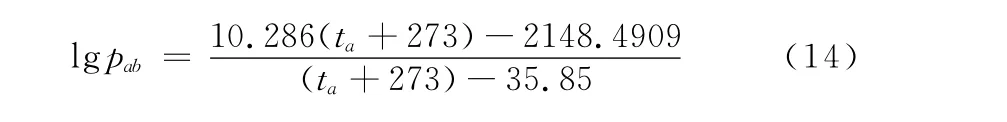
3.1 温度影响

假设风速为0.1m／s，湿度为65%，温度从0℃变化至35℃，在此情况下，利用修正前、后的公式（3）、（13）分别模拟运动员的热感觉，模拟的结果如图1。

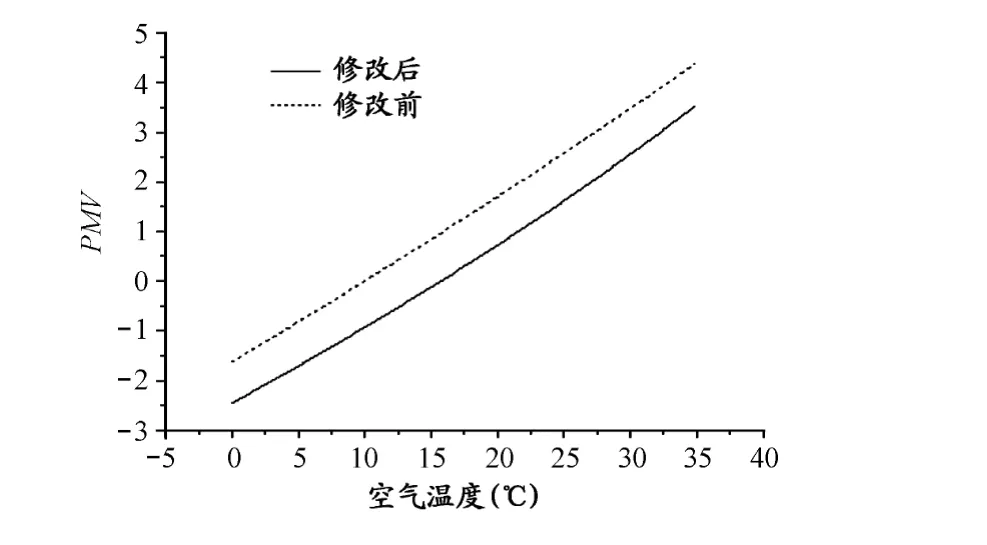
图1 本研究PMV随环境温度的变化示意图Figure 1.PMV Vary with Temperature Change

从图1可知，PMV与温度之间的关系为线性关系，从公式计算PMV对ta的变化率为:

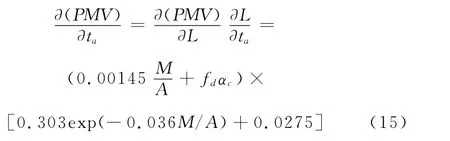
由此可见，变化率为常数。随温度升高，PMV值不断增大，这是由于温度升高，导致皮肤对外辐射、呼吸失热量减少，从而使PMV值升高。温度对于人体热舒适性的影响很大，大约4℃的变化会引起数值为1的PMV的变化。

3.2 风速的影响

假设25℃，65%的湿度，风速在0.05～0.2m／s之间变化，利用修正前后的公式（3）、（13）分别模拟运动员的热感觉。

由图2可知，温度湿度不变时，随着风速增加，PMV下降，趋势为先快后慢。这是由于风速增加，对流散热系数增加，加强了对流散热，减少了人体热负荷。对于曲线先急后缓的情况，则由风速和对流换热系数关系式决定:

由此可见，随着风速增加，对流换热系数增加速度也是先急后缓，从而解释了PMV的变化情况。

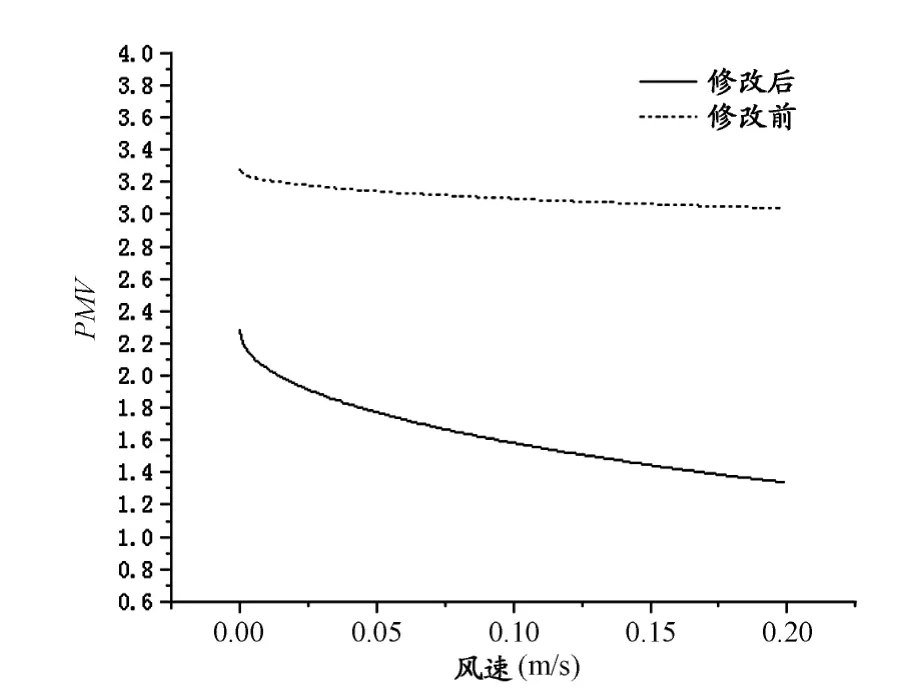
图2 本研究PMV随环境风速的变化示意图Figure 2.PMV Vary with Wind Speed Change

3.3 湿度的影响

假设25℃，风速为0.1m／s，湿度在40%～80%之间变化，利用修正前、后的公式（3）、（13）分别模拟运动员的热感觉，模拟的结果如图3:

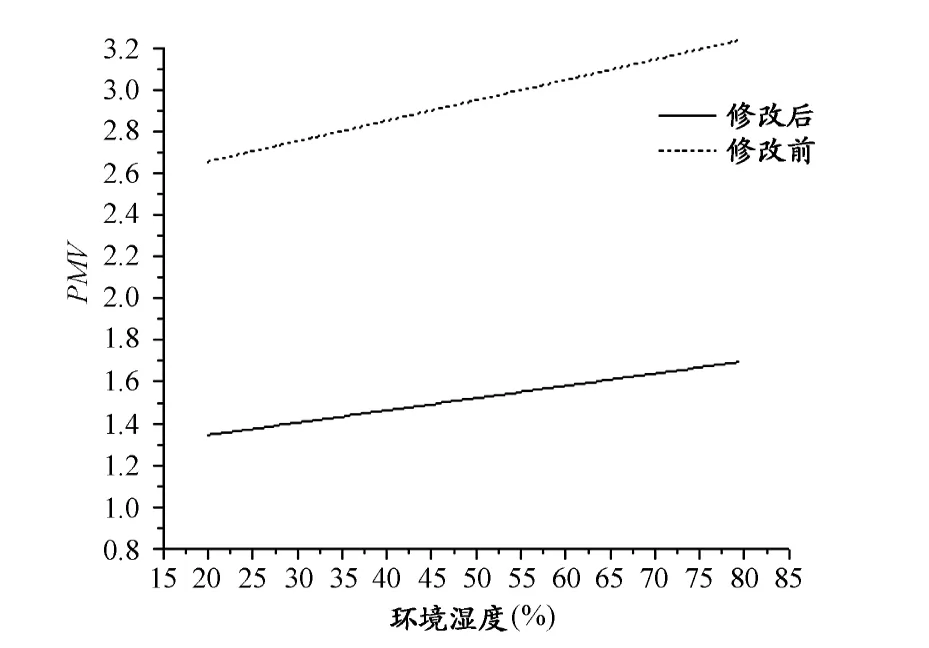
图3 本研究PMV随环境湿度的变化示意图Figure 3.PMV Vary with Humidity Change

由图3可知，PMV随湿度呈线性变化，对PMV公式求导

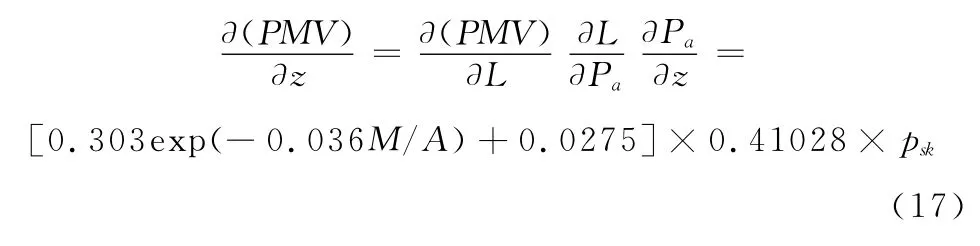
在给定条件下，M／A、psk均为常数，则＝ const，则PMV随湿度线性变化。PMV随湿度增大而增加，这是由于湿度增加抑制了体表扩散的作用，减少了散热，PMV增加。

3.4 小结

由图1至图3可知，对处于相同条件下的运动人体，相比于Fanger模型，修改后的模型计算得到的PMV值更低，这是因为:首先，修改后的模型所计算的皮肤温度更高，加强了体表扩散作用；其次，修改后模型的服装热阻比Fanger模型的更小，增加了对流辐射散热，人体失热增多，使得PMV降低。本研究提到Fanger模型在大运动量时PMV评价偏高，修正后的模型在“采暖通风与空气调节设计规范”规定的空调参数下更接近热中性，符合实际情况，较为合理。

依据“采暖通风与空气调节设计规范”中规定，空调室内参数标准:温度的变化范围为24℃～28℃；相对湿度的变化范围为40%～60%；风速要求小于0.2m／s。比较3种热环境因素变化对PMV的影响，从图1可知，4℃的环境温度变化将引起PMV值约1的变化；从图2可知，0.2 m／s的风速变化引起PMV值约0.6的变化；图3中20%的相对湿度的变化引起PMV值约0.2的变化，对比可知，在可调控范围内，温度对于人体热感觉的影响最大。

4 模型的实验验证

为了比较Fanger模型及修正后模型在实际应用中的准确性，以及不同环境因素对于PMV的影响程度，需要对实际情况中运动人群的舒适性进行调查、统计及分析。

4.1 实验对象

选取某大学的羽毛球馆作为实验地点，以每天在馆内进行羽毛球健身的人群作为实验对象，由于每天进行羽毛球健身的人员不同，故实验对象非固定。整个实验从2014年9月开始至2014年12月结束，原因是这期间羽毛球场馆内温、湿度变化较大，温度变化范围为16℃～29℃；湿度变化范围为36%～82%，实验数据可以反映多数馆内环境下运动人群的热舒适情况。由于本次实验是针对羽毛球馆内运动人体的测量，故风速变化不大，保持在0.15m／s以下。选择其中16天共338人进行测试，共获得295份有效数据。

4.2 实验方法

4.2.1 环境参数测量

利用日本KANOMAX智能环境测试仪6533-2G记录环境参数，包括温度、湿度及风速（表2）。

表2 本研究智能环境测试仪参数一览表Table2 The Parameters of Intelligent Environmental Test Equipment

4.2.2 热舒适性调查问卷

由于实验对象每天非固定，在身高、体重、衣着等方面存在差异，故每个受试对象采用调查问卷的形式。问卷内容包括姓名、性别、年龄、身高、体重、衣着、运动时间等基本参数，在运动结束时填写基本参数和热感觉，在很热、比较热、有点热、不冷不热、有点冷、比较冷、很冷中选择，表3为11月4日某位受试者的样卷。

表3 本研究受试者热舒适性调查表样卷一览表Table 3 The Sample for Thermal Comfort Questionnaire

4.2.3 实验流程

每天测量时间均为晚上19:00～21:00，受试对象均为在此期间进行羽毛球健身运动的人群，利用智能环境测试仪在此期间每隔15min进行环境参数的测量，测量位置均为靠近场馆中心的位置，在受试对象结束羽毛球运动后对其进行热舒适性调查问卷的访问。

4.3 数据处理与分析

4.3.1 环境参数的处理

由于羽毛球场馆内运动散热以及场馆保温性等因素的影响，环境参数会有小幅度变化，故在测试期间选取运动过程中的不同时间点进行多次测量并取平均值（表4）。

4.3.2 热舒适数据的处理与分析

由于实验对象为普通羽毛球健身运动人群，由参考文献取新陈代谢率 M＝5.5Mets［18］。计算时，根据每个受试的身高、体重、衣着以及每天的环境参数，利用计算机编程获得每个受试在两种模型中的PMV值，然后分别与实际测量的PMV值比较。

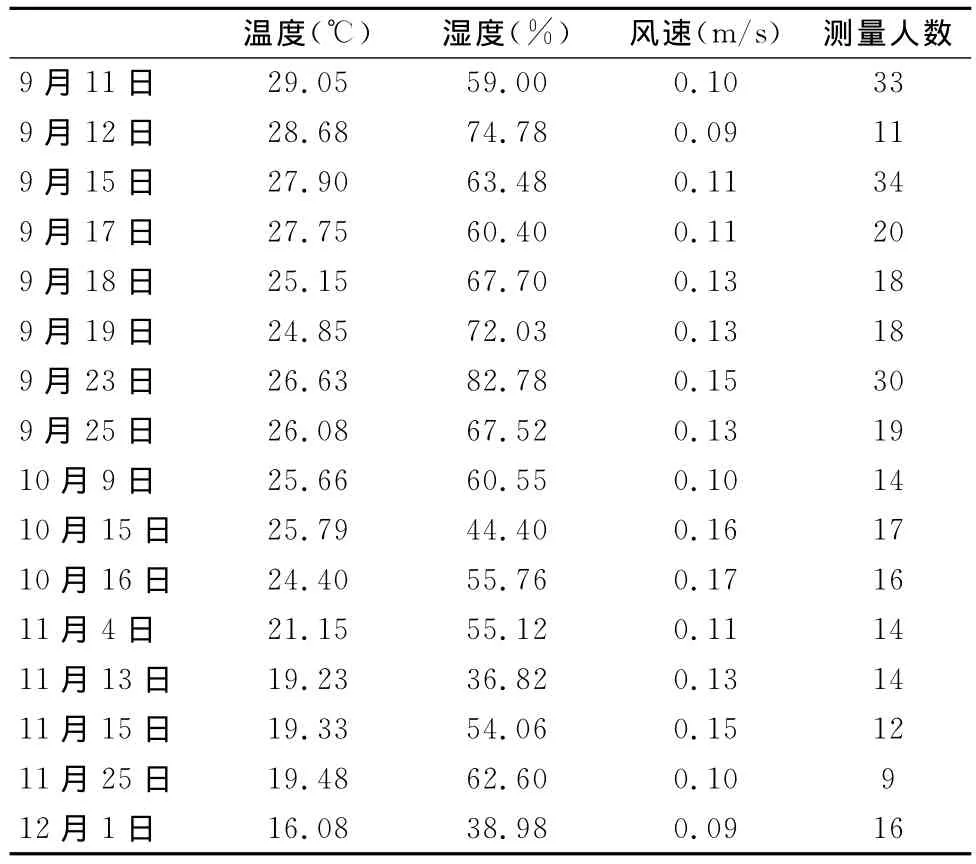
表4 本研究实验期间环境参数一览表Table 4 The Environment Parameters During Experiment

4.3.2.1 单日个体热舒适度比较

由于测试时段较长，测试对象较多，本研究以10月15日为例，受测对象共21人。由于部分数据（如身高体重等）未填写，故热舒适度无法计算，实际有效人数为17人。利用环境参数及运动员身高体重分别计算不同模型下的热舒适度，并与实测热舒适度进行比较（表5）。

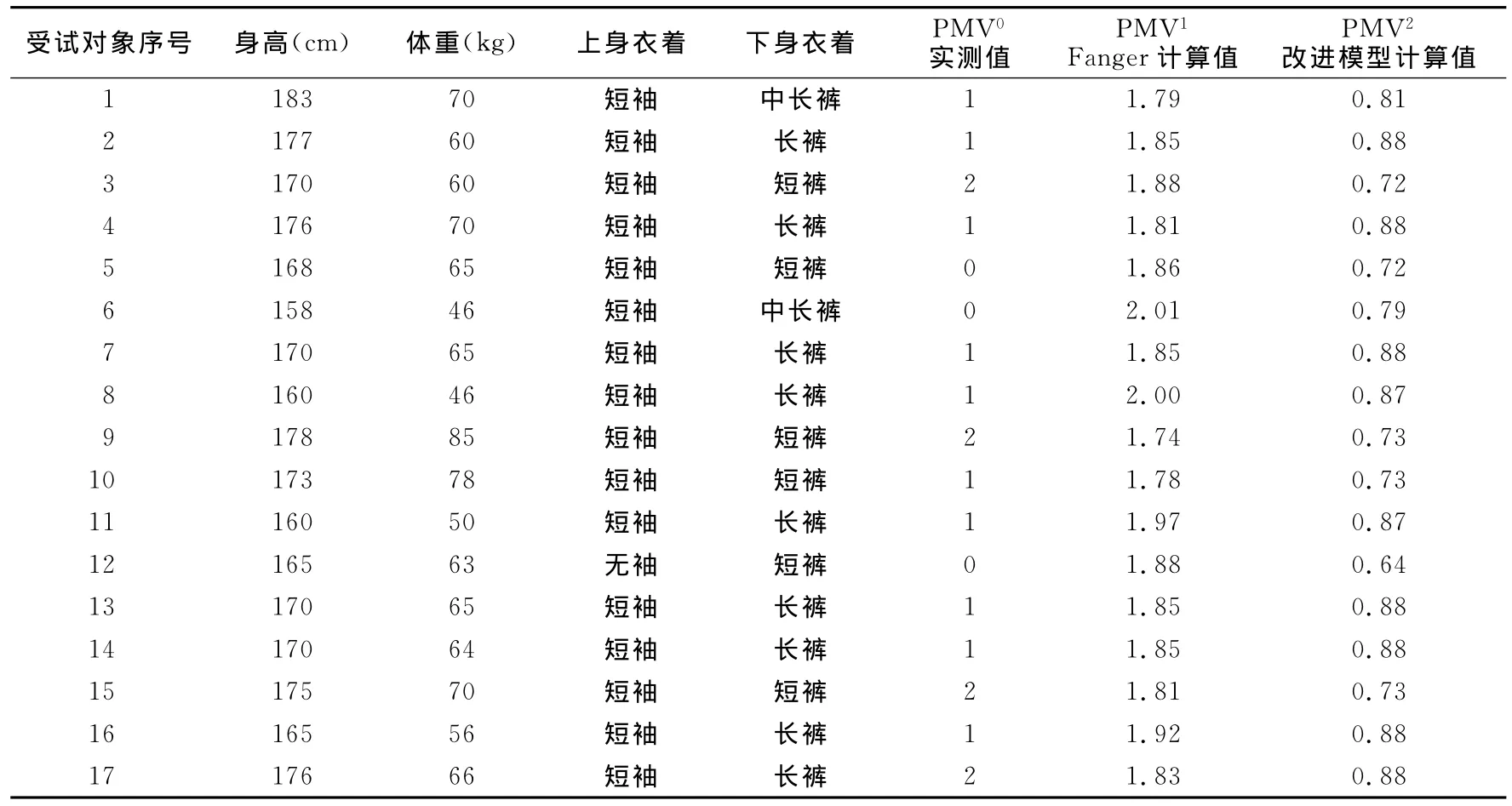
表5 本研究受试者10月15日测试数据汇总一览表Table 5 The Summaries of Data on October 15th

由表5可知，相比于Fanger模型计算值，绝大多数人员实测PMV值与改进模型计算PMV值更为接近。由于热舒适是人对周围热环境所做的主观满意度评价，极少数受试对象实测值与模型计算值出现差异是正常的，这也是Fanger提出PPD（Predicted Percentage of Dissatisfied）指标的主要原因，PPD表示人群对热环境不满意的百分数。

4.3.2.2 整个测试周期热舒适度对比

定义S为模拟所得的舒适度相对于实际测量PMV的偏差值，其表达式如下:

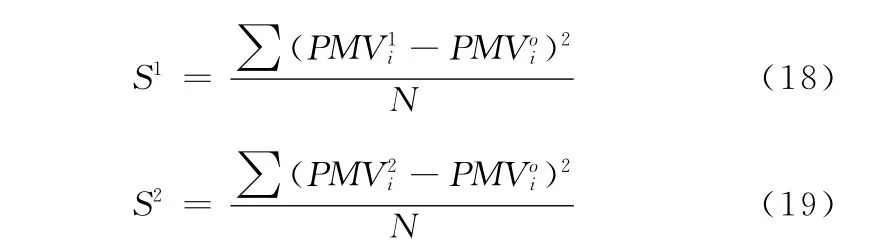
其中，S1代表Fanger模型相对于实际测量P MV的偏差值；S2代表修正后模型相对于实际测量P MV的偏差值；为Fange模型计算得出的人体舒适度；为修正后模型计算得出的人体舒适度；为问卷调查得出的实际舒适度；下标i代表第i个人；N为每次实验中的测量人数。S1和S2的大小代表了两种模型与实际测量结果的接近程度。利用式（1 8）、（1 9）计算每天中的模型偏差S1，S2（表6）。为问卷调查得出的实际舒适度；下标i代表第i个人；N为每次实验中的测量人数。S1和S2的大小代表了两种模型与实际测量结果的接近程度。利用式（18）、（19）计算每天中的模型偏差S1，S2（表6）。

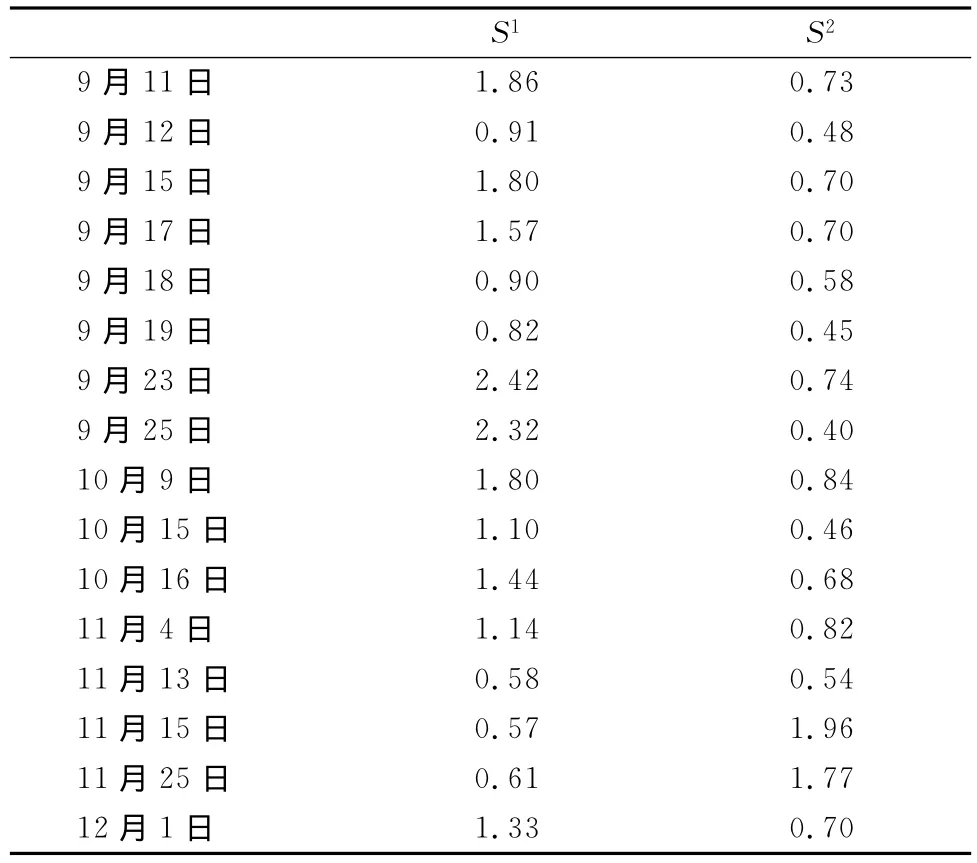
表6 本研究不同模型与实际测量值偏差一览表Table 6 The Deviation of Different Models Compared with Measured Value

由表6可知，比较每天中不同模型的热舒适性偏差，不同温度下，两种模型相对于实际情况的精确度不同。在较高的环境温度中，如9月23日和9月25日，修正后模型相对于实际舒适度的偏差远小于Fanger模型；随着环境温度降低，Fanger模型的偏差降低，修正后模型的偏差没有明显变化，在20℃左右的环境温度下，两者偏差基本相同。

5 结论

通过模型模拟和实验验证，修正模型较Fanger模型结果更加合理并接近实际。

1.理论与实验数据表明，在较高的环境温度下，Fanger模型与实际运动人体的热舒适性偏差很大；而修正后模型在高、中、低温度段均与实际偏差较小。

2.在体育场馆的环境下，由于场馆风速变化较小，对于同一运动，温度、相对湿度对运动人体PMV影响显著，其中，温度对PMV的影响最大。通过空调系统调节温、湿度是提供舒适运动环境较为有效的方法。

3.温度、湿度以及新陈代谢速率与PMV的关系均呈现线性关系，风速与PMV的变化关系为幂函数曲线，其中，随着温度、湿度以及新陈代谢速率的增大而上升；PMV随风速增大而下降。

6 总结

本研究根据运动人体新陈代谢速率大、衣着热阻小、排汗量大、辐射环境复杂以及呼吸急促的特点，对Fanger模型中辐射、体表扩散的模型进行了修正，并对修正模型进行了理论探究和实验验证。结果表明，修正后的新模型较Fanger模型更加合理并接近于实际。在实际情况中，可以用该模型较好地预测不同环境参数下不同项目运动人体的热舒适情况，尤其在竞技比赛中便于对环境做出合理的调控。

［1］纪秀玲.人居环境中人体热感觉的平均及预测［M］.北京:中国疾病预防控制中心，2003:1-2.

［2］刘荣向.基于新陈代谢率及皮肤温度的人体热舒适实验研究［D］.青岛:青岛理工大学，2010.

［3］林登光.针织运动服面料舒适性 （热阻湿阻）评价指标研究［J］.福建轻纺，2011，（5）:44-48.

［4］牛润萍，陈其针，张培红.热舒适的研究现状与展望［J］.人类工效学，2004，（1）:40-42.

［5］邱曼，武建民，常绍勇，等.环境温度、运动负荷等因素对人体排湿率影响的研究［A］.第6届全国人机环境系统工程学术会议论文集［C］.北京:2003:283-285.

［6］文学军.动态热环境人体热感觉的模糊综合评判［J］.清华大学学报（自然科学版），1998，（5）:25-29.

［7］许景峰.浅谈PMV方程的适用范围［J］.重庆建筑大学学报，2005，（3）:15-20.

［8］薛殿华.空气调节［M］.北京:清华大学出版社，1991:31-37.

［9］周翔.动态热环境下人体热反应机理研究—气流湍流度的影响［D］.北京:清华大学，2005.

［10］AINSWORTH，HASKELL，HERRMANN，et al.2011compendium of physical activities:a second update of codes and MET values［J］.Med Sci Sports Exe，2011，43（8）:1575-1581.

［11］FANGER P O.Calculation of thermal comfort，Introduction of a basic comfort equation［J］.ASHRAE Transact，1967，73（2）:1-4.

［12］HUIZENGA C，HUI Z，ARENS E.A model of human physiology and comfort for assessing complex thermal environments［J］.Build Environ，2001，36（6）:691-699.

［13］International Standard ISO 7730，Moderate thermal environmentsdetermination of the PMV and PPD indices and specification of the conditions for thermal comfort［S］.

［14］MEICLEUX，MALEHAIE，CANDAS.温热环境中平均皮肤温度的预报（译文）［J］.四川生理科学杂志，1988，4（1）:45-46.

［15］MACPHERSON R K.The assessment of the thermal environment.A review［J］.Bri J Indust Med，1962，19（3）:151-164.

［16］NADEL，MITCHELL.Differential thermal sensitivity in the human skin［J］.Pflügers Archiv，1973，340（1）:71-76.

［17］NICOL.Adaptive thermal comfort standards in the hot-humid tropics［J］.Energy Build，2004，36（7）:628-637.

［18］Standard 55-2004，Thermal environmental conditions for human occupancy［S］.