超声相控线阵换能器参数对换能器接收灵敏度的影响
杨天雪
(福建省特种设备检验研究院,福建 福州 350008)
超声相控线阵换能器参数对换能器接收灵敏度的影响
杨天雪
(福建省特种设备检验研究院,福建 福州 350008)
文中将超声相控线阵换能器视为复合材料,将复合材料力学与声学理论相结合,通过计算超声相控线阵换能器模型的等效力学参数,推导出了线阵换能器声波方程的解;并依据声波方程的解进一步得出了超声相控线阵换能器参数对线阵换能器接收灵敏度的影响规律。
超声相控阵;线阵换能器;接收灵敏度
1 引言
超声相控阵换能器是超声相控阵设备的关键部分。但是关于超声相控阵换能器中声波传播的研究还不够深入,还没有给出超声相控线阵换能器声波方程的解,也就无法得到超声线控线阵换能器的参数对换能器接收灵敏度的影响,从而对设计高接收灵敏度的换能器制作提供理论指导。根据超声线阵换能的结构,文中将超声相控线阵换能器视为一种特殊的复合材料,根据复合材料力学的相关知识计算出了声波方程求解所需的弹性模量、剪切模量、泊松比和密度的等效值,代入声波方程解出超声相控线阵换能器声波方程的解。进而根据声波方程的解详细讨论线阵超声换能器各个参数对换能器接收灵敏度的影响规律。
2 超声相控线阵等效力学参数的计算
超声相控阵换能器由4个基本部分组成,包括:匹配层(铜)、胶层、压电陶瓷、背衬层,如图1所示。三轴坐标系如图所示,因为X1轴垂直于纸面指向纸外,所以未在图上标示出来。设压电陶瓷块个数为N ,每个陶瓷块的高为h,宽为a,长为l ,中心间距为d。匹配层、胶层和背衬层的厚度分别为,h g和h b。
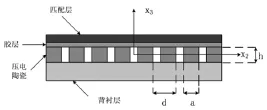
图1 线阵换能器示意图
2.1等效弹性模量的计算
轴的伸长与力的关系为:

其中E 为弹性模量,A 为截面积,l为轴的长度。
弹簧的伸长与力的关系为:

比较式(1)与式(2)可知,若将轴等效为弹簧,则等效刚度:

匹配层、胶层、背衬层都是各向同性的,它们的弹性模量分别为Em、Eg和Eb。因为陶瓷为厚度方向极化,在横向是各向同性的,所以陶瓷的弹性模量分为厚度方向的弹性模量Ept与横向的弹性模量分别表示陶瓷、匹配层、胶层、背衬层在X1、X2、X3方向的截面积。材料的弹性模量包括相互垂直的三个方向上的分量,下面分别进行计算。
(1)X1方向
将陶瓷、匹配层、胶层、背衬层都等效为弹簧,则它们X1方向的等效刚度为:
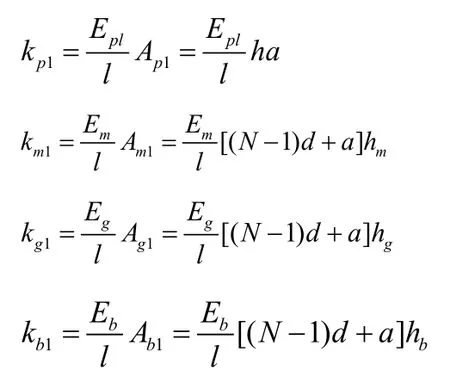
在X1方向,陶瓷、胶层、匹配层和背衬层可视为弹簧并联,则沿X1方向换能器总的等效刚度为:
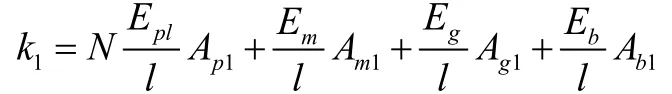
则沿X1方向的等效弹性模量为:
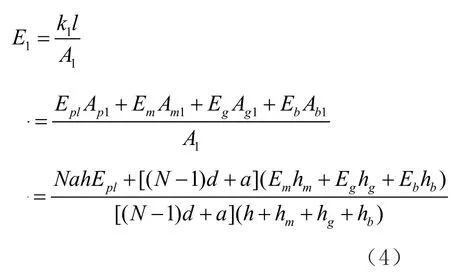
(2)X2方向
将陶瓷、匹配层、胶层、背衬层都等效为弹簧,则它们在X2方向的等效刚度为:
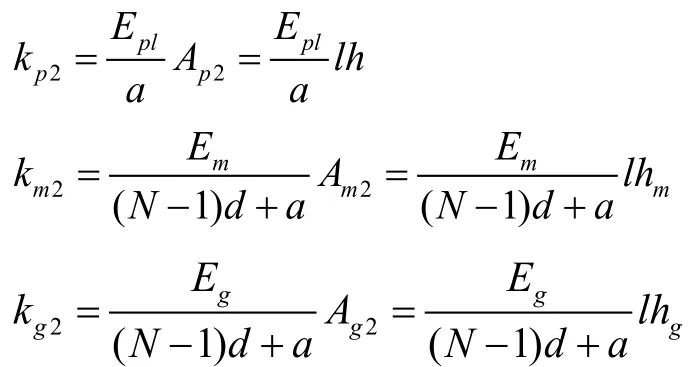
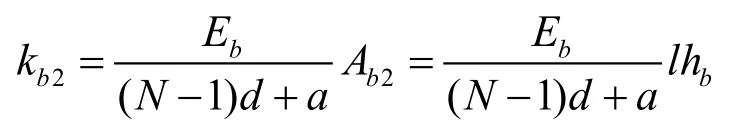
在X2方向,陶瓷、胶层、匹配层和背衬层可视为N个陶瓷等效的弹簧串联后再与胶层、匹配层和背衬层等效的弹簧并联,则沿X2方向换能器总的等效刚度为:
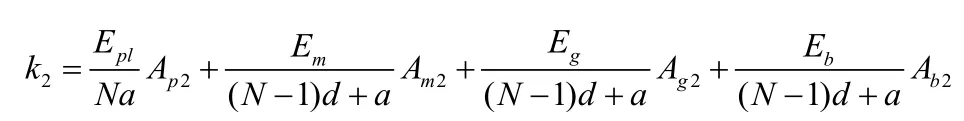
则沿X2方向的等效弹性模量为:
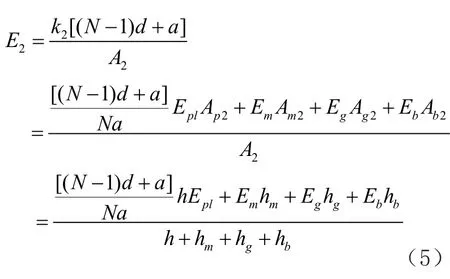
(3)X3方向
将陶瓷、匹配层、胶层、背衬层都等效为弹簧,则它们在X3方向的等效刚度为:
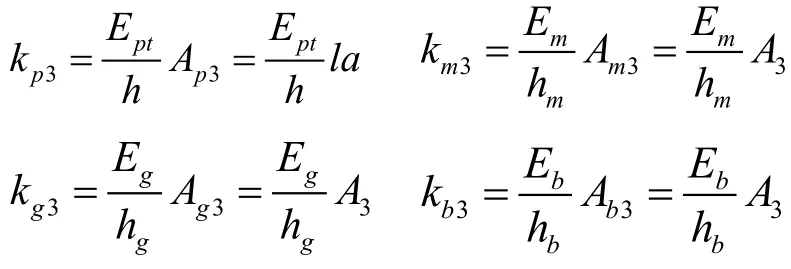
在X3方向,陶瓷、胶层、匹配层和背衬层可视为N个陶瓷等效的弹簧并联后再与胶层、匹配层和背衬层等效的弹簧串联,则沿X3方向换能器总的等效刚度为:
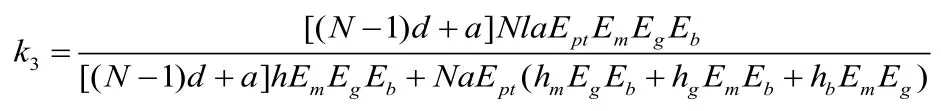
则沿X3方向的等效弹性模量为:
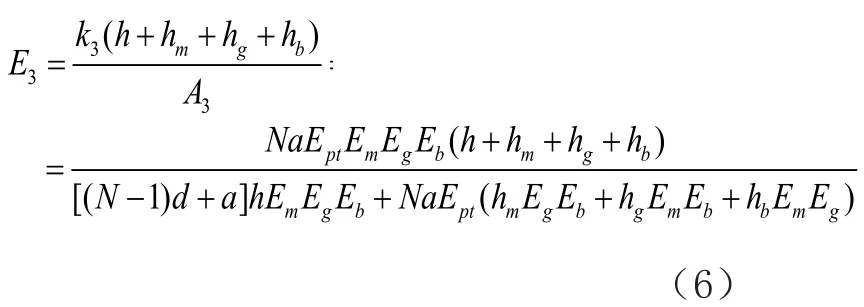
2.2等效泊松比的计算
匹配层、胶层、背衬层都是各向同性的,它们的泊松比分别为vm、vg和vb。因为陶瓷为厚度方向极化,在横向是各向同性的,所以陶瓷的泊松比分别为。
设换能器在X2方向的应变为ε,则X1方向的应变ε'推导如下:
若四种材料未粘结,则陶瓷、匹配层、胶层和背衬层在X1方向上的应变应分别为。而由于材料之间的粘结力,则四种材料在X1方向上应变为相同的ε'。陶瓷、匹配层、胶层和背衬层在X1方向的弹性模量分别为Epl、Em、Eg和Eb。由力的平衡可知:
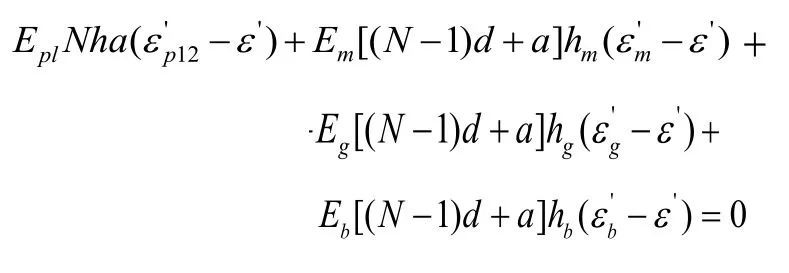
解得:
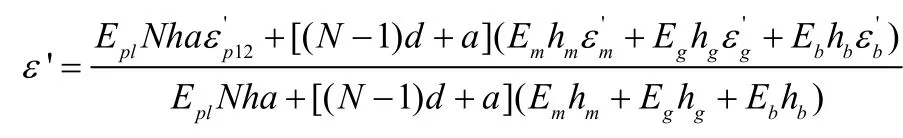
所以
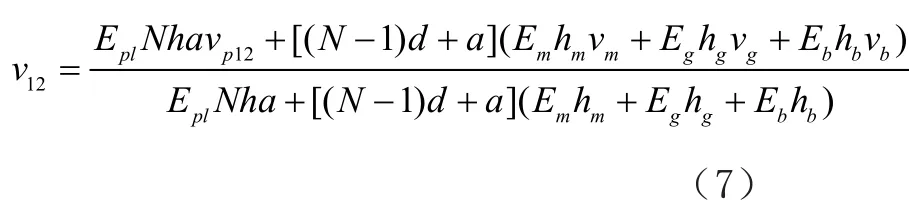
因为换能器在X3方向的伸长为陶瓷、匹配层、胶层和背衬层伸长的总和,所以可得:
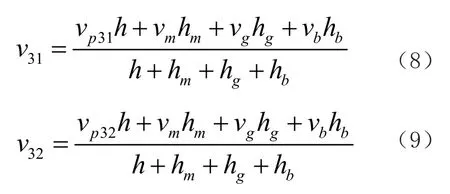
如果物体内有一个平面,在这个平面的对称点上弹性性能相同,这样的材料就具有一个弹性对称面;如果材料具有2个正交的弹性对称面,这种材料称为正交各向异性材料。可知超声线阵换能器X1X3平面和X2X3为正交弹性对称面,所以可以将线阵换能器视为正交各向异性材料。正交各向异性材料的泊松比和弹性模量满足如下的关系式[]:
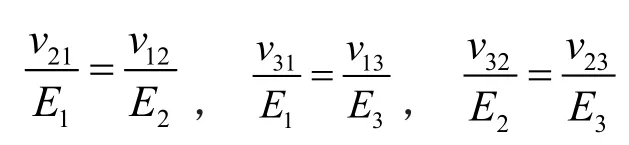
已知v31、v32、v12,由以上三式可求得:
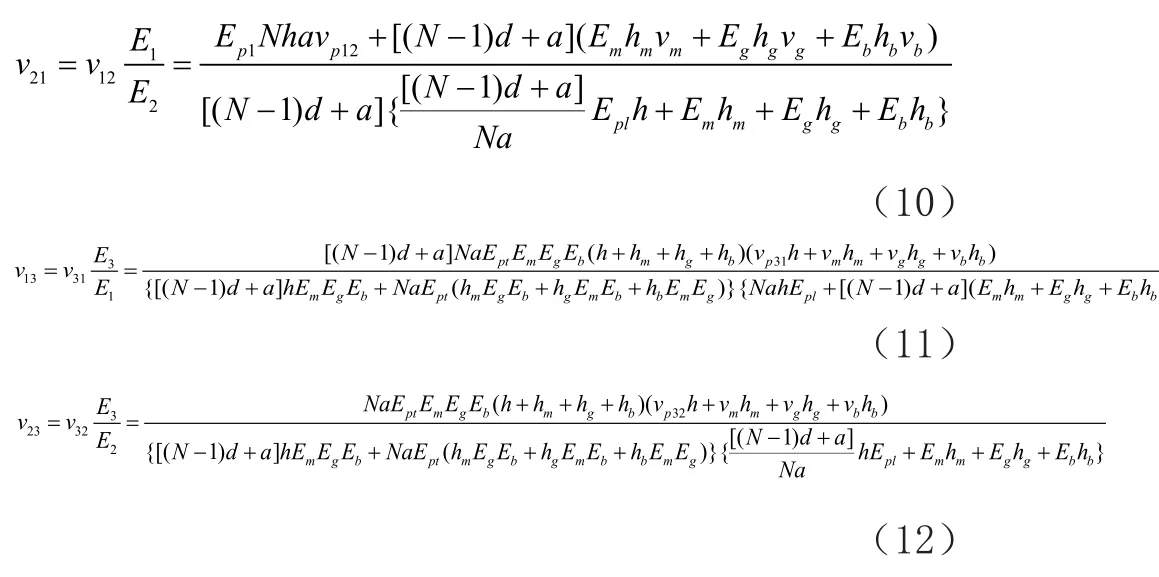
2.3等效剪切模量的计算
匹配层、胶层、背衬层都是各向同性的,它们的剪切模量分别为Gm、Gg和Gb。因为陶瓷为厚度方向极化,在横向是各向同性的,所以陶瓷的剪切模量分别为厚度方向的剪切模量Gpt与横向的剪切模量Gpl。可知扭转角与扭矩的关系为[2]:

其中φ为扭转角,β为与h/ b 有关的系数,可通过查表求得,l 为长度,h 与b 如图2所示。
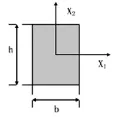
图2 材料截面尺寸示意图
材料的剪切模量包括相互垂直三个方向上的分量,下面分别进行计算。
(1)X1方向
将陶瓷、匹配层、胶层、背衬层都等效为扭簧,则它们X1方向的等效刚度为:
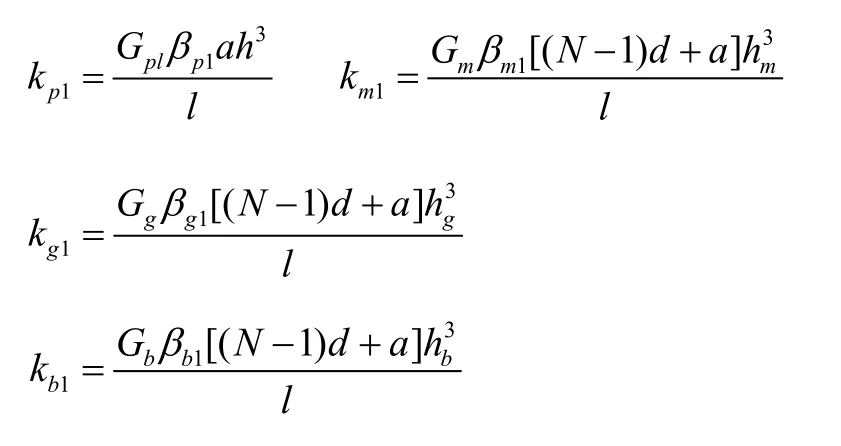
在X1方向,陶瓷、胶层、匹配层和背衬层可视为扭簧并联,则沿X1方向换能器总的等效刚度为:
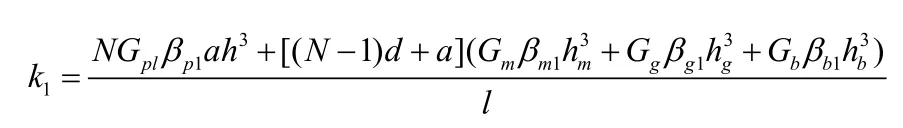
X1方向的等效剪切模量:
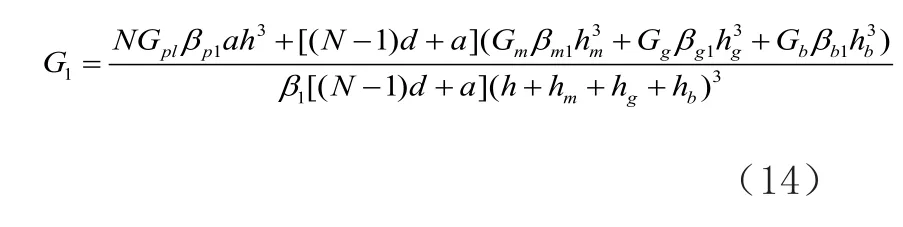
(2)X2方向
陶瓷、胶层、匹配层和背衬层X2方向的等效刚度为:
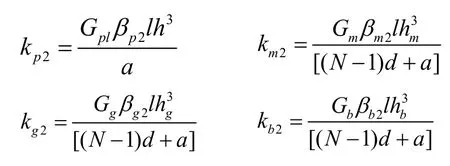
在X2方向,陶瓷、胶层、匹配层和背衬层可视为N个陶瓷等效的扭簧串联后再与胶层、匹配层和背衬层等效的扭簧并联,则沿X2方向换能器总的等效刚度为:
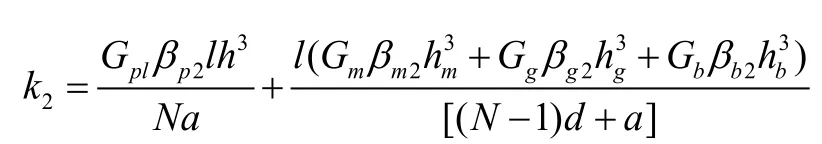
X2方向的等效剪切模量:
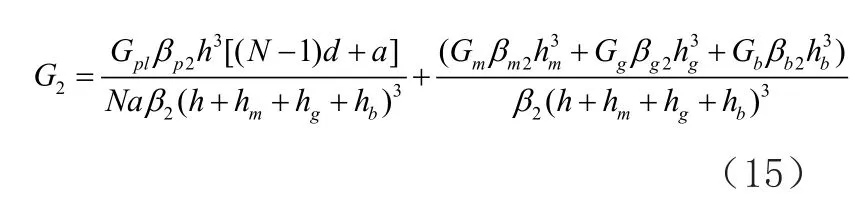
(3)X3方向
陶瓷、胶层、匹配层和背衬层在X3方向的等效刚度为:
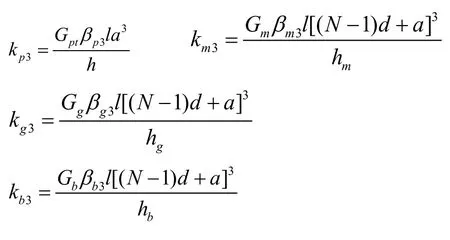
在X 3方向,陶瓷、胶层、匹配层和背衬层可视为N个陶瓷等效的扭簧并联后再与胶层、匹配层和背衬层等效的扭簧串联,则沿X3方向换能器总的等效刚度为:
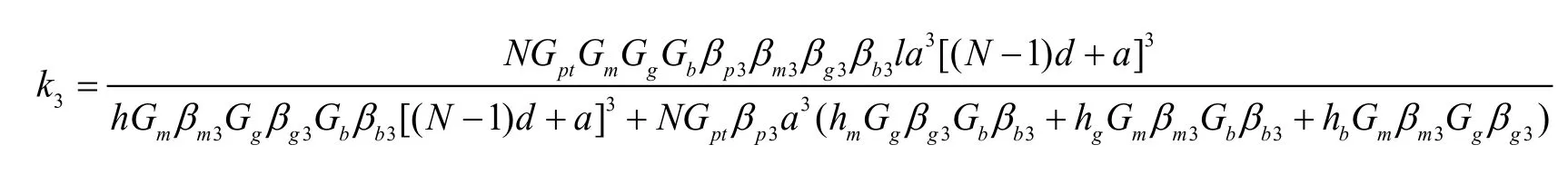
X3方向的等效剪切模量:
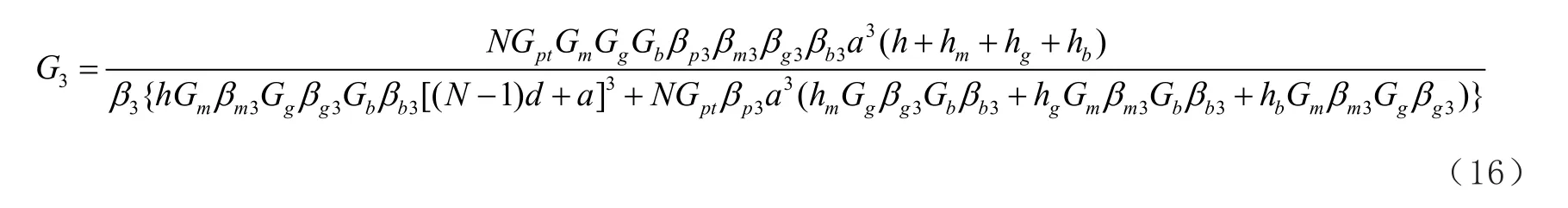
2.4等效密度的计算
设陶瓷、匹配层、胶层和背衬层的密度分别为ρp、ρm、ρg和ρb,可得换能器的等效密度为:
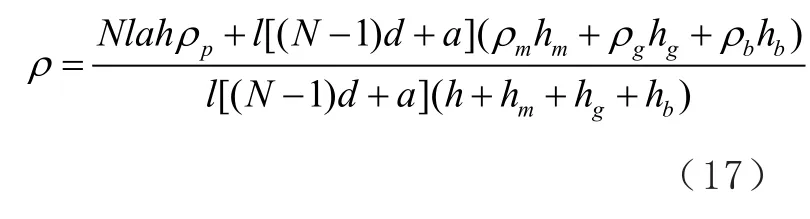
3 超声相控线阵换能器声波方程的解
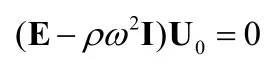
其中ρ为介质的密度,ω为角频率,E 是 3×3的矩阵,单元由平面波的波矢方向和介质的劲度系数确定。I 是3×3的单位矩阵,U0是U0i组成的列矢量,它的方向是质点振动的方向,称为偏振方向。
求U0的非零解,正是求矩阵E的特征值问题。因为陶瓷是沿厚度方向极化,且声波的传播方向为厚度方向,所以研究沿X3方向传播的平面波,
即k1=k2=0,可得:

则(E-ρω2I)U=0成为:
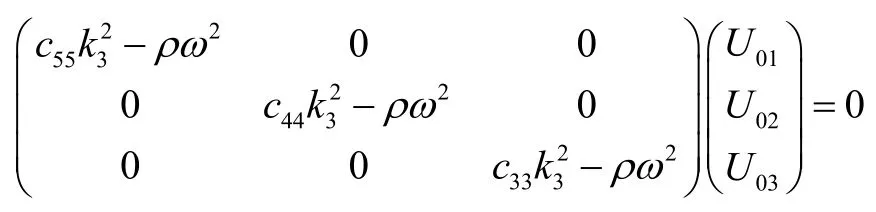
为了得到U0i的非零解,上式中的行列式应为零,即:
上式是特征方程,它是解耦的,可以得到3个特征值。
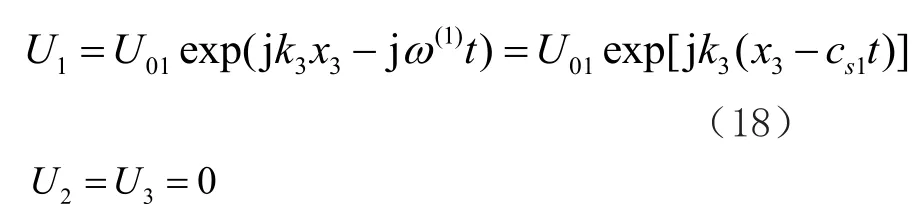
偏振方向与传播方向垂直,是横波,cs1是偏振方向为X1方向的横波速度。
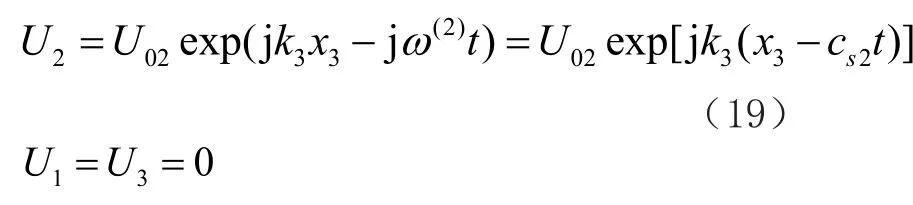
偏振方向与传播方向垂直,是横波,cs2是偏振方向为X2方向的横波速度。

偏振方向与传播方向一致,是纵波,cl是偏振方向为X3方向的纵波速度。因为陶瓷的振动方向为厚度方向,也就是X3方向,为纵波,所以在文中笔者对纵波进行详细的研究。质点速度。
由1.2已知超声换能器可视为正交各向异性材料,正交各向异性材料的柔性常数与工程弹性常数有如下关系[]:

由文献可知压电陶瓷PZT-5H的刚度矩阵为[4]:

又知材料的弹性矩阵与柔顺矩阵互为逆阵

那么
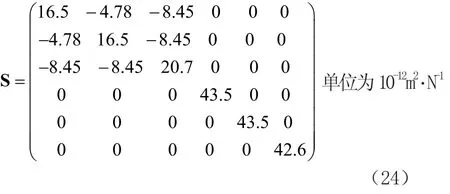
陶瓷为正交各向异性材料,则由式(1)与式(4)可得陶瓷的材料参数:
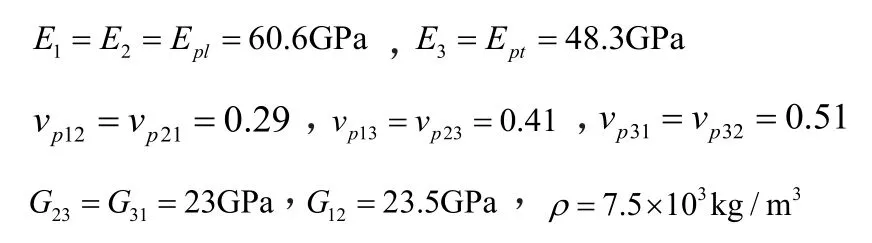
如果选择的匹配层材料为铜,那么:
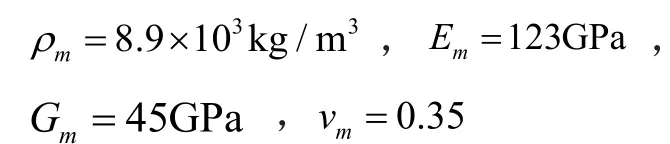
胶层的参数:
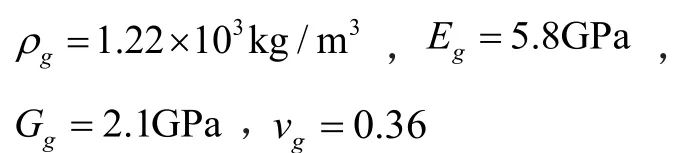
背衬层的材料为环氧树脂加钨粉,它的性能参数为[]:
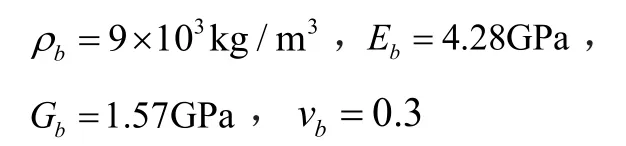
根据以上材料的参数和等效参数的计算公式就可得到线阵换能器的等效参数,再由公式(1)与公式(3)可计算得到线阵换能器的等效刚度矩阵,进而得到线阵换能器声波方程的解。
4 阵列参数对换能器接收灵敏度的影响规律
其余的应变分量为零。
由公式[]
其中D 为电位移矢量,e 为压电应变常数,x 为应变。
可知x 增大,D 增大。又由[8]
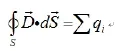
知D 增大,电荷数量增加,电流变大,所以电压V变大。那么换能器接收灵敏度增大[]。
由公式(25)得ε33的幅值为,可知ε33与k3成正比。波矢的分量为纵波速度,可知k3与cl成反比。又知换能器的接收灵敏度与ε33成正比,所以换能器接收灵敏度与cl成反比。由于换能器阵列参数的变化会引起各个等效参数变化,从而改变波动方程的解,进而对声速产生影响;所以可以通过研究线阵换能器纵波声速cl随换能器参数的变化趋势来得到换能器接收灵敏度随换能器参数的变化趋势。
4.1背衬层厚度的影响
选择陶瓷厚度为1.26mm,长度为30mm,宽度为1.8mm,阵元间距为2.9mm,粘贴后胶层的厚度为0.015mm,阵元数目为8。图3为换能器其它参数为给定值的情况下声速随背衬层厚度的变化。
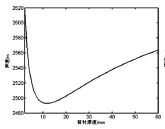
图3 声速随背衬层厚度的变化
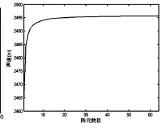
图4 声速随阵元数目的变化
由图3可以看出,声速随背衬层厚度的变化是先减小再增大,有一个最小值。而声速与换能器接收灵敏度成反比,那么,换能器接收灵敏度随背衬层厚度的变化有个最大值。在换能器的其它参数不变的情况下,背衬层的厚度有一个最优值,在这个厚度下,换能器的接收灵敏度最大。那么在设计换能器时,就可以根据其它参数值,通过以上的公式计算得到最优化的背衬层厚度值,使换能器的接收灵敏度达到最大。
4.2阵元数目的影响
阵元数目对线阵换能器的声速也会产生影响。图4是陶瓷厚度为1.26mm,长度为30mm,宽度为1.8mm,阵元间距为2.9mm,粘贴后胶层的厚度为0.015mm,背衬层厚度为10mm的情况下声速随阵元数目的变化。由图4可知,声速随阵元数目的增大而增大,在阵元数目小于8时,声速变化比较快;而当阵元数目大于等于8时,声速趋于一个确定的值,不再随阵元数目的变化而变化。这说明换能器接收灵敏度随阵元数目的增大而减小,但是当阵元数目大于等于8时,阵元数目的变化对换能器的接收灵敏度影响趋于零。一般相控阵换能器的阵元数目都大于等于8,所以在实际设计中,可以不考虑阵元数目对换能器接收灵敏度的影响。
4.3阵元宽度的影响
换能器的声速还会受到阵元宽度变化的影响。图5是陶瓷厚度为1.26mm,长度为30mm,粘贴后胶层的厚度为0.015mm,背衬层厚度为10mm,阵元数目为8,阵元间距分别为2.9mm和0.29mm时声速随阵元宽度的变化。由图5可知,声速随阵元宽度的增大而减小,这说明其它参数确定时,换能器接收灵敏度随阵元宽度的增大而增大。比较图5中的(a)图和(b)图可以看出,两条曲线形状完全一致,对于相同的d/a,声速相等,这说明阵元宽度对换能器接收灵敏度的影响只与宽度和间距的比值有关,而与阵元宽度的具体值无关。
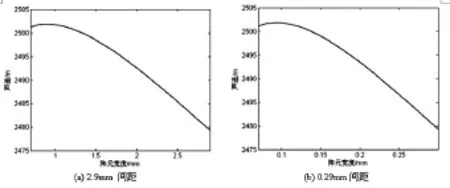
图5 声速随阵元宽度的变化
4.4阵元间距的影响
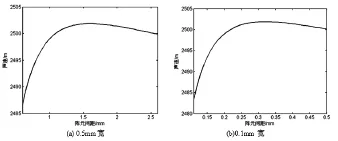
图6 声速随阵元间距的变化
阵元间距变化也会对换能器的声速产生影响。图6是陶瓷厚度为1.26mm,长度为30mm,粘贴后胶层的厚度为0.015mm,背衬层厚度为10mm,阵元数目为8,阵元宽度分别为0.5mm和0.1mm时声速随阵元间距的变化。由图可知,在阵元间距小于等于三倍阵元宽度时,声速随阵元间距的增大而增大,这说明其它参数确定且阵元间距小于等于三倍阵元宽度时,换能器接收灵敏度随阵元间距的增大而减小;而当阵元间距大于三倍阵元宽度时,声速随阵元间距的增大而减小,这说明其它参数确定且阵元间距大于三倍阵元宽度时,换能器接收灵敏度随阵元间距的增大而增大。比较图6中的(a)图和(b)图可以看出,两条曲线形状完全一致,对于相同的d/a,声速相等,这说明阵元间距对换能器接收灵敏度的影响只与间距和宽度的比值有关,而与阵元间距的具体值无关。
因为阵元间距和宽度对换能器声速的影响只与它们的比值有关,所以图7给出了换能器的其它参数为给定值,换能器声速随阵元间距与宽度比值的变化。由图7可知在阵元间距为三倍阵元宽度的时候,声速有一个最大值,也就是说换能器接收灵敏度有一个最小值。在阵元间距与宽度比由3变大或变小时,换能器接收灵敏度都增大。
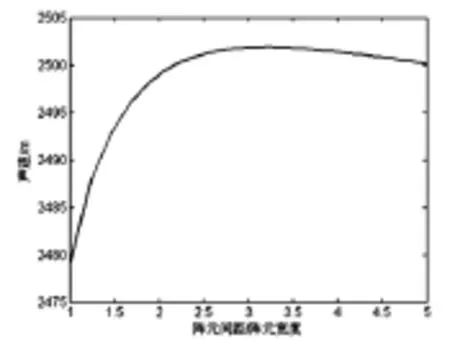
图7 声速随阵元间距与宽度比值的变化
5 结论
文中对超声相控阵换能器进行简化,将陶瓷、匹配层、胶层、背衬层都等效为弹簧,根据弹簧的串并联理论计算出超声相控线阵换能器模型的等效力学参数。然后把复合材料力学与声学理论相结合,得到了线阵换能器声波方程的解。根据声波方程的解发现线阵换能器的接收灵敏度与纵波声速成反比,从而利用超声相控线阵换能器参数对纵波声速的影响间接得到其对接收灵敏度的影响。文中的工作开拓了一条超声相控阵换能器理论研究的新思路,对开展超声相控阵换能器的研究及设计有着一定的指导意义。
[1] 沈观林,胡更开.复合材料力学[M].北京:清华大学出版社,2006:38.
[2] 许德刚.材料力学[M].郑州:郑州大学出版社,2007:86.
[3] 张海澜.理论声学[M].北京:高等教育出版社,2007:436.
[4] Stephen A.Wi l son,Renaud P.J.Jourdain,Qi Zhang,et al.New materials for micro-scale sensors and actuators: An engineering review[J].Materials Science and Engineering:R: Repor ts,Vol.56,Issues 1-6,21 June 2007:1-129.
[5] Leigh-Ann Or r,Anthony J.Mulhol land,Richard L.O’Leary,et al.Harmonic analysis of lossy, piezoelect ric composite transducers using the plane wave expansion method[J]. Ul t rasonics,In Press,Cor rected Proof,Avai lable onl ine 15 March 2008.
[6] Denis E.Cuche Proc.Determinat ion of the Poisson's ratio of f il led epoxy and composite materials[C].SPIE 1212,315 (1990).
[7] 张福学编.现代压电学[M].北京:科学出版社,2002:85.
[8] 张晓华.大学物理一本通[M].杭州:浙江大学出版社,2005:96
[9] 栾桂冬,张金铎,王仁乾.压电换能器和换能器阵[M].北京:北京大学出版社,2005:310.
The Influence of Parameters of Linear Ultrasonic Phased Array Transducer on Receiving Sensitivity
YANG Tian-Xue
(Fujian Special Equipment Inspection and Research Institute, Fuzhou 350008, Fujian, China)
Based on mechanics of composite materials and acoustic theory, equivalent mechanical parameters of linear ultrasonic phased array transducer are calculated by regarding linear ultrasonic phased array transducer as composite material. Then the solution of acoustic wave equation of ultrasonic linear phased array transducer is derived. Based on it, the influence rules of parameters of linear phased array transducer on receiving sensitivity are obtained.
Ultrasonic phased array; Linear transducer; Receiving sensitivity
2015-09-07
杨天雪,男,福建省特种设备检验研究院,容管中心副主任,博士

