基于EMD的应变重构方法实验分析

韩大利

（北京航空航天大学可靠性与系统工程学院，北京100191）

0 引言

目前，结构健康监测技术在航空航天领域应用十分广泛，它是实现单机寿命监控管理的重要技术手段。在结构健康监控管理中，不管是结构诊断还是工程结构预测，都需要准确估计结构关键部位的健康状况，以此来确定维修计划。但是在实际的工程应用中，采用传感器对结构的健康状态或飞行参数进行检测往往存在监测点有限、关键部位不可达等困难。考虑到数据采集和分析的成本，或待测点位置不可达等实际问题，我们只能得到个别位置的动态响应。因此，间接推导出关键点处的动态响应成为结构健康监测中一个关键组成部分。

为了能够达到结构健康监控管理的要求，必须对应力重构技术进行研究。本论文研究的是基于经验模态分解（Empirical Mode Decomposition，EMD）的应变重构方法。该方法通过对系统结构进行有限元分析，利用成熟的EMD技术，结合已知点的应力应变数据，推断关键部位附近的应力和载荷，从而实现对系统关键部位的应力重构分析，进而可用于结构有无损伤的判断、损伤位置的确定和损伤程度的推断。在此基础上进行系统寿命的估计，达到结构健康监测的目的。

1 基于EMD的应变重构方法

1．1 光纤布拉格光栅传感器

光纤布拉格光栅传感器是近几年发展起来的新型传感器。其基本原理就是将光纤的特定位置制成折射率周期分布的光栅区，这样一来，特定波长的光波将被反射。反射的中心波长信号跟光栅周期和纤芯的折射率有关。布拉格波长对于应力、温度等负荷是相当敏感的，应变和压力影响布拉格波长是由光栅周期的伸缩以及弹光效应引起的，外界应力、压力的变化也会引起波长的变化。

相比较之前常用的应变片而言，光纤布拉格传感器的优点是：质量轻，极大地降低结构试件埋入传感器的重量；抗干扰，无需屏蔽电、磁；分布式，凭借现代通信可多路复用，进一步降低了重量和成本；可挠曲，满足结构要求；埋入后对结构影响小；集成化，可望实现小型化。

因此，在本文的实验部分我们采用该传感器进行数据的采集。

1．2 振型分析及模态函数的获得

在应变重构方法中，我们需要计算固有频率及结构的振型矩阵，获得模态矩阵后便能得到模态对应关系，以此来为后续的模态分解提供依据。

有限元分析的基本做法是将结构划分为若干单元，通过计算单元质量矩阵和刚度矩阵，进而得到整体结构的刚度矩阵和质量矩阵，从而计算得到结构的固有频率及振型矩阵。

经验模态分解方法可以有效提取非线性、非稳定信号的瞬时特征。经验模态分解方法的基本思想是将原始信号分解成一组固有模态函数。一个固有模态函数是一个具有零平均值并且两个零点之间只有一个极值点的函数。这些固有模态函数组成了原始信号完整的几乎正交的基，这将使得不同频率的信号在时间域内得以呈现，而这些是在傅里叶变换和小波系数中不能观察到的。模态分解过程在现有文献中均可查到，在此不做赘述。

当给定一个应变时间序列y（t）时，经过经验模态分解后，可以得到下面的表达式：

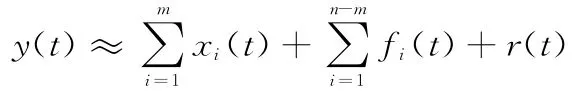
式中，xi（t）是模态响应同时也是固有模态函数；fi（t）是非模态响应的固有模态函数。

1．3 应变重构方法的提出

通过有限元分析，就可以得到如下的振型矩阵：

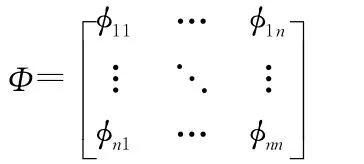
该振型矩阵是通过求解一个特征跟问题获得的，即：

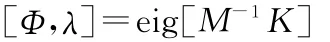
Φ的物理意义可以做如下解释：每一列代表一个模态，列中的每一组分代表结构中一个自由度的位移分量。当结构的离散拓扑关系和自由度的数目确定后，模态矩阵就会变成一个常数，那么，一个坐标到另一个坐标的位移比率也将是一个常数。两坐标之间的模态响应关系可以用下面的表达式来表示：

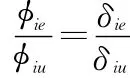
结合应变—位移方程，就可以得到下面的关系式：

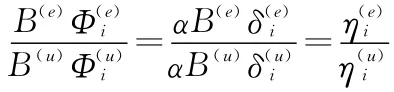
获得关键部位的应变模态响应函数后，就可以通过模态叠加得到该部位的应变时序信号，即：

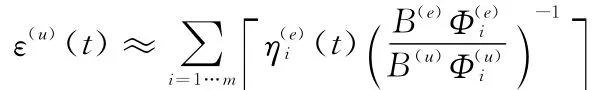
2 对于应变重构方法的实验分析

本文以铝合金悬臂梁为实验模型，探讨监测点位置对重构结果的影响。悬臂梁一端为自由端，另一端为固定端，并在三个位置分别布贴传感器。

传感器布贴示意图如图1所示。

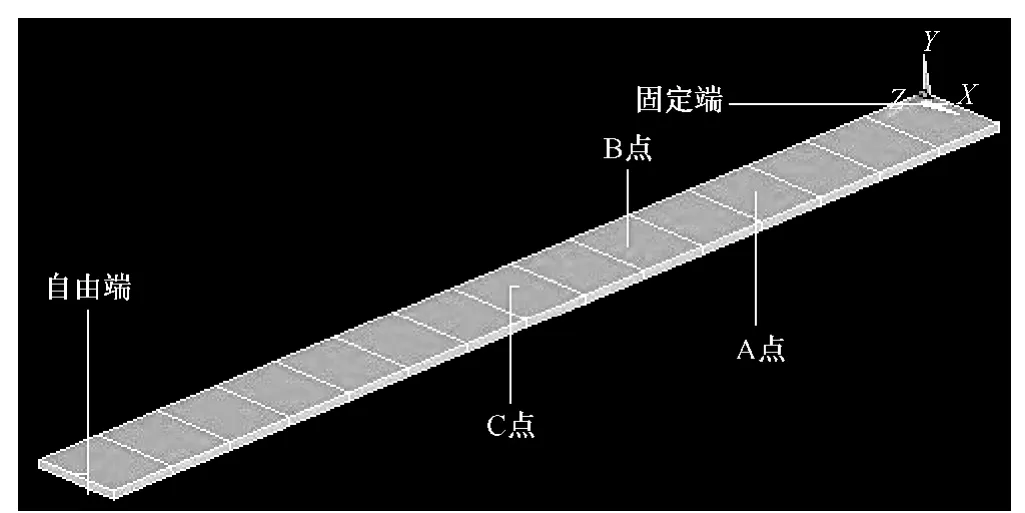
图1 传感器布贴示意图

取B点作为关键部位，通过A、C两点采集得到的应变数据，分别对B点进行重构实验。激励信号我们采用在自由端施加冲击的方法获得。

分析结果如图2所示。

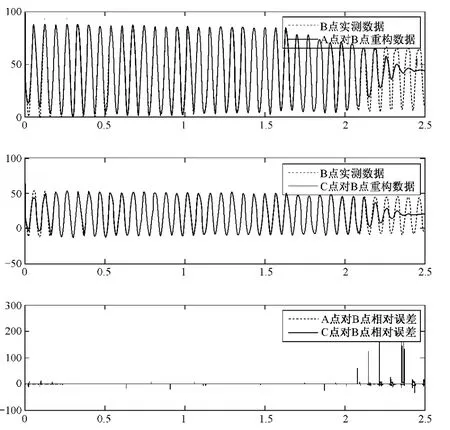
图2 分析结果

从结果图我们可以看到，用A点和用C点重构得到的B点的应变数据，与B点处实测应变数据基本吻合，数据一致性较好，这很好地体现了文中提出的应变重构方法的有效性和准确性。从A、C两点重构结果与B点实测应变数据之间的统计分析数据来看，A点对B点的重构数据与实测数据的相关系数为0．949 1，而C点对B点的重构数据与实测数据相关系数为0．948 3，这说明A点的重构结果要优于C点的重构结果。然而其数据误差相差并不大，这也说明了使用文中提出的应变重构方法，监测点位置的选取对关键部位应变重构基本不存在影响。

同时我们也看到数据尾部出现较大的偏差，这是EMD算法中的端点延拓问题，由于不是本文的研究重点，因此不做进一步讨论。

3 总结与展望

重构技术是结构健康监控技术的重要组成部分，也是实现飞机单机寿命监控的重要技术手段。本文以悬臂梁为实验模型，研究应变重构方法，并通过选取不同的监测点测量应变数据，对同一处关键部位进行重构实验。实验结果表明，该因素并不会对重构结果带来大的影响。当然，文中只是对不同监测点位置进行了研究，在今后的研究工作中，还应当对其他因素进行探讨，比如改变悬臂梁尺寸、改变结构的形状、对结构进行损伤处理、采用不同的激励方式等。对应变重构方法的研究，对于完善结构健康监测理论有着重要的意义，也为工程中的损伤特征提取与识别提供了依据。

［1］刘文珽，王智，隋福成，等．单机寿命监控技术指南［M］．北京：国防工业出版社，2010．

［2］杨智春，于哲峰．结构健康监测中的损伤检测技术研究进展［J］．力学进展，2004，34（2）：215－223．

［3］李开泰，黄艾香，黄庆怀．有限元方法及其应用［M］．西安：西安交通大学出版社，1992．

［4］杨永锋，吴亚锋．经验模态分解在振动分析中的应用［M］．北京：国防工业出版社，2013．

［5］He J J，Guan X F，Liu Y M．Structural response reconstruction based on empirical mode decomposition in time domain［J］．Mechanical Systems and Signal Processing，2012（28）：348－366．