赏析高中数学联赛中的复数问题

林海

中图分类号：G633.6 文献标识码：A 文章编号：1672-8882（2015）04-031-02

复数具有代数形式、三角形式、指数形式等多种表述方式，所蕴含的实际意义是以新的视角、新的途径沟通了代数、三角和几何等内容之间的联系，由此，该知识点是各类考试（尤其是数学联赛和自主招生）选拔优秀学生的的一个重要内容。

一、复数知识

（一）复数的表示形式与运算

代数形式：

三角形式：

指数形式：

题1（2013年四川8）已知 是虚数单位， ，把复数 的共轭复数记为 ，则 =_________.

解 ，由周期性知每相邻4个数的和为0，则 ， ，

题2（2010年浙江15）设 是虚数， ，则 的实部取值范围为_____

解 法一：设 ， ，由题意 是实数，

则 ，得

①当 时， ，无解

②当 时， ，得

法二：由复数除法的几何意义知 表示的点与 表示的点关于 轴对称，且到原点的距离都为1，由加法的几何意义知 是以 为邻边的菱形的对角线，又 是实数，则 的实部是 的实部的2倍，所以 的实部取值范围为 。

（二）复数的模与共轭复数

题3（2014年山东7）已知 ，则 的值为_______

解 由乘法的性质知 ， ，

题4（2011年湖北5）设 是模为2的复数，则 的最大值与最小值的和为_________

解 由 ，知 ，

，故

其最大值为 ，最小值为 。故所求为4。

（三）复数的单位根

题5（2010年山东7）已知 为复数， 为虚数单位。若 ，则当 为实数时， 的最小值为（ ）

A. B.3 C. D.

解 法一：设 ，由题意 ， 得 ，则

， 表示辅角为60°或120°的复数，至少当 时 为实数，所以

法二：由复数及其加法的几何意义知 ， 的终点在单位圆上， 与 关于 轴对称且在单位圆上，因为 ，则 与 夹角为-60°或240°， 的辅角为60°或120°， 略

二、复数方法

（一）复数在代数中的应用

题6（2012年天津9）如果复数 满足 ，且 ，其中 为实数，则 的最大值是________

解 法一： ，则 ，求 的最大值，可以借助线性规划求解，代表单位圆的动点 ，求 的最大值，转化为相切的问题即得

法二：令 ，则 ，所以最大值为

法三：由不等式 ，得最大值为

（二）复数在几何中的应用

题7（2012年辽宁7）设

，则 在复平面内所对应区域的面积是__________

解 ，设 ，则有 ，

。

易知 ，故 ，所以复数 对应的点形成的区域是以点（7，8）为圆心，4为半径的圆面，其面积为 。

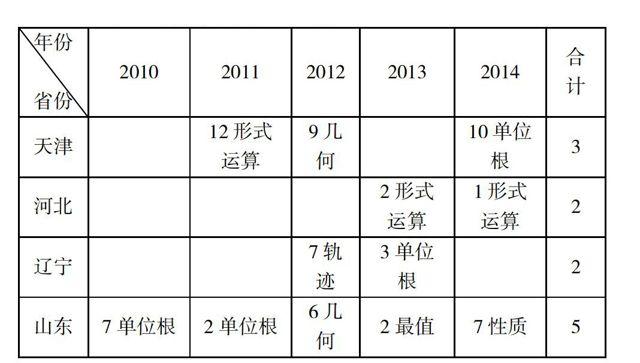
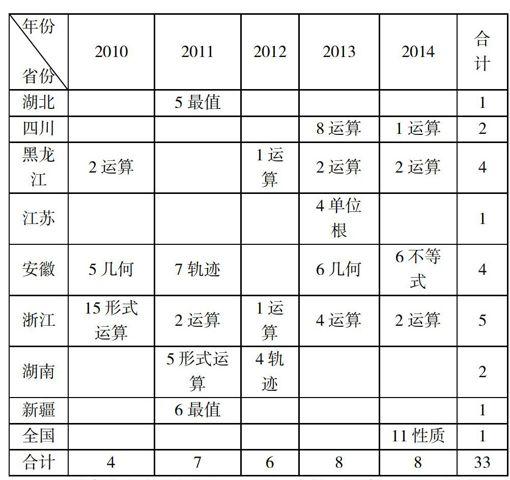
三、近五年各省对复数考查情况

在預赛中考查的省份有：山西、吉林、福建、江西、河南、陕西、甘肃、贵州，我们不难发现今年考查的比重频率有上升趋势，考查基本计算和灵活应用性质和几何意义居多，尤其是14年在全国联赛一试中已经以解答题的形式出现，让很多人无从下手，笔者预测15年各省预赛试题中将会大面积的出现复数的考查，这势必要引起考生和教师的注意。

练习题

1.（2011年湖南5）已知复数 满足 ，复数 的虚部为2，则 为实数的条件是 _________

2.（2012年山东6）设 为一对不相等的共轭复数，且 ， 为实数，则 的值为（）

3.（2013年辽宁3）设 均为非零复数，令 ，若 ，则 的值为（ ）

4.（2012年湖南4）设实数 ，如果复平面上的动点 满足 则动点 的轨迹是（ ）

5.（2013年安徽6）设复数 满足 的实部与虚部之比为 ，其中 是虚数单位， ，则 的最大值为________

6.（2014年全国11）确定所有的复数 ，使得对任意复数 均有

附答案：1. 2.3 3. 4.焦距为4的椭圆 5. 6.

参考文献：

[1]2011年高中数学联赛备考手册[M].华东师范大学出版社，2010.

[2]2012年高中数学联赛备考手册[M].华东师范大学出版社，2011.

[3]2013年高中数学联赛备考手册[M].华东师范大学出版社，2012.

[4]2014年高中数学联赛备考手册[M].华东师范大学出版社，2013.

[5]2015年高中数学联赛备考手册[M].华东师范大学出版社，2014.

[6]刘诗雄.奥数教程第五版（高二年级）[M].华东师范大学出版社，2011.