粒度特性参数与粒度分布均匀程度的关系

侯英，印万忠，朱巨建，姚金，王余莲，吴凯



粒度特性参数与粒度分布均匀程度的关系

侯英1，印万忠2, 3，朱巨建1，姚金3，王余莲3，吴凯2

(1. 辽宁科技大学矿业工程学院，辽宁鞍山，114051；2. 福州大学紫金矿业学院，福建福州，350108；3. 东北大学资源与土木工程学院，辽宁沈阳，110004)

对Rosin−Rammler(R−R)粒度特性方程中的参数和应用解析几何和偏导数的方法进行研究，分析粒度特性参数和与粒度的关系及对粒度分布的影响，并运用一些实例验证所得结果。研究结果表明：当颗粒直径<>exp(1/)时，粒度特性参数对筛上累积产率起主要影响作用，越大，下降越快，粒度分布越均匀；当0＜＜1 mm时，越小，下降得越快，粒度分布越均匀。研究结果可完整地分析各种不同的破碎磨矿条件下产品的粒度分布特征。

粒度特性参数；粒度分布；粒度特性方程；偏导数

若颗粒群是由单一粒径的颗粒所组成，则称其为单分散的颗粒，或称其为粒度均匀的颗粒。事实上，任意颗粒群都是由多种不同大小的颗粒所组成，只能定性称其为具有一定均匀性的颗粒，且粒度分布越宽均匀性越差[1]。粒度特性方程能够概括复杂的筛分分析数据。因此，可用它计算表面积、颗粒数、平均粒度及某一粒级的筛分效率等[2−3]。影响产品粒度分布的指标有很多，磨机结构方面有：磨机规格、型式、衬板；操作方面有：介质形状、尺寸配比及材质、介质充填率、磨机转速、返砂比、分级效率、矿浆的浓度、粘度、温度以及矿浆的化学成分[4−11]；还包括不同破碎磨矿方式等。粒度特性参数可直接反映样品的粒度分布特征。段希祥[12]研究了高登粒度特性方程的参数及变化规律，但未针对罗辛−拉姆勒方程(Rosin− Rammler, R−R)的粒度特性参数进行研究。段希祥[13]解释和取决于物料性质和粒度因次。袁致涛 等[14−15]对粒度特性参数和进行解释，认为为与产物粒度相关的参数，为均匀性系数，表示粒度分布范围的均匀程度，越小，粒度分布越均匀，但未具体分析粒度特性参数和粒度分布的关系。本文作者在总结前人研究的基础上，应用解析几何和偏导数的方法研究粒度特性参数和对粒度分布之间的定量关系，并评价不同碎磨方式的实际工作情况，可为选择最佳的碎磨方式提供依据。

1 粒度特性方程

当产品粒度较细时，适合运用R−R分布描述其粒度特性，R−R方程为[16−17]

式中：0为粒度大于的正累积产率，%；为颗粒直径或筛孔宽，μm；为与产物粒度相关的参数；为与物料性质有关的参数。

2 粒度特性参数的理论意义

2.1 解析几何法

将式(1)取2次对数可得

运用解析几何法，在上述直线任意选取2个点，得：

式中：1和2分别为粒度大于1和2的颗粒的正累积产率，%；1和2分别为所选取的点的颗粒直径或筛孔宽，μm。

从式(2)可以看出：表示降低的速度，但未考虑和的影响，为直线的截距，截距越大，越小。当粒度较细(<>exp(1/))时，越大，越小，下降越快，粒度分布越均匀；越小，越大，下降越慢，粒度分布越不均匀。

当粒度较细时，对粒度分布起主要的影响，当粒度较粗时，对粒度分布起主要的影响。粒度特性参数和反映出被磨物料的性质和磨矿条件对粒度分布的影响。

2.2 偏导数法

应用数学偏导数法，研究粒度特性参数和对筛上累积产率的影响，定量表示粒度特性参数、筛上累积产率和粒度之间的关系，通过对粒度特性参数的研究判断物料的粒度分布特性。

由粒度特性方程可知：越大，越小；越大，也越小。

第1种情况，假设=0.2不变，令=0.8，1.0，1.2，1.4，1.6和1.8；第2种情况，保持=1.0不变，令=0.1，0.3，0.5，0.7，0.9和1.1，结果分别如图1和图2所示。

由图1和图2可以看出：当粒度较细时，对筛上累积产率的影响较小，而对的影响较大，由此看出对的变化起主要的影响作用；随粒度的增大，对的影响作用应变大，但根据粒度特性方程的性质，和共同影响，因此，和应作为整体来分析。

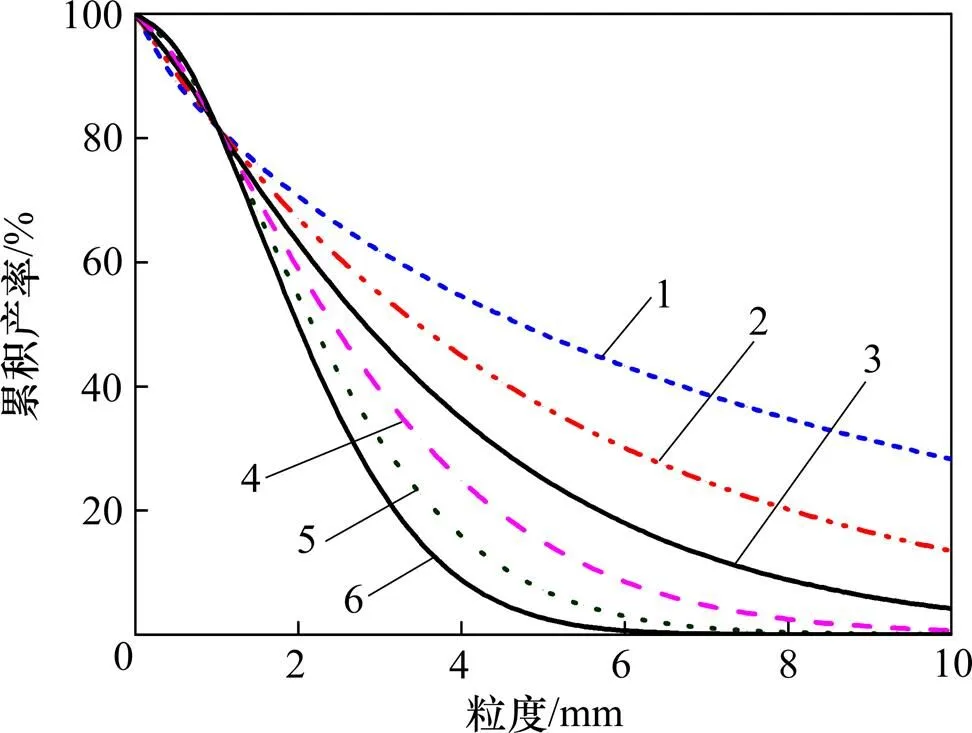
n: 1—0.8; 2—1.0; 3—1.2; 4—1.4; 5—1.6; 6—1.8

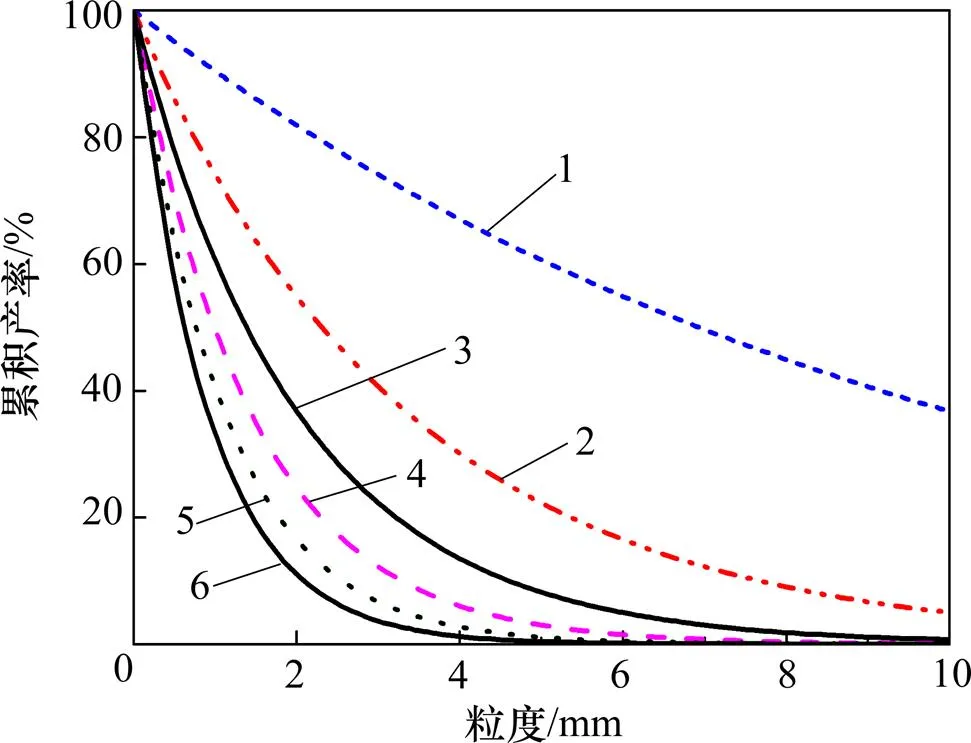
b: 1—0.1; 2—0.3; 3—0.5; 4—0.7; 5—0.9; 6—1.1

结合偏导数法对粒度特性方程进行分析，可更全面地研究粒度特性参数对粒度分布的影响。

对粒度特性方程中的求偏导数得

由式(5)可以看出：当0＜＜1 mm时，＜0，＞ 0，说明越大，越大，下降越慢，粒度分布越不均匀；当=1 mm时，=0，=0，与无关；当＞1 mm时，＞0，＜0，说明越大，越小，下降越快，粒度分布越均匀。该函数的意义为：在假设和不变时，对筛上物料累积产率的影响。上述偏导数为关于粒度的函数。

对粒度特性方程中的求偏导数得

考虑和对降低的影响，取粒度＞1 mm，若参数对下降的影响小于对下降的影响，则对求偏导数的数值要小于对求偏导数的数 值，则：

由式(7)~(9)可知：当<<时，对降低的影响起主要的作用，越大，越小，下降越快，粒度分布就越均匀；在>>时，对下降影响起主要作用，越大，越小，下降越快，粒度分布就越均匀；当0＜＜1 mm时，越小，越小，下降越快，粒度分布越均匀；在=附近时，和共同影响的降低，共同影响粒度的分布情况。将=定义为粒度特性分界粒度。

3 粒度特性参数理论意义的验证

3.1 不同碎磨方式对邦铺钼铜矿粒度分布的影响

对西藏墨竹工卡邦铺钼铜矿石进行高压辊磨和颚式破碎试验，并对2种粉碎产品进行粒度分析，其正累积粒度特性曲线与R−R方程拟合回归结果分别如图3与表1所示[18]。

由图3和表1可以看出：高压辊磨产品比颚式破碎产品的粒度细，高压辊磨产品中粒度小于0.074 mm的粒子质量分数比颚式破碎产品的高7.01%，粒度分布更均匀。

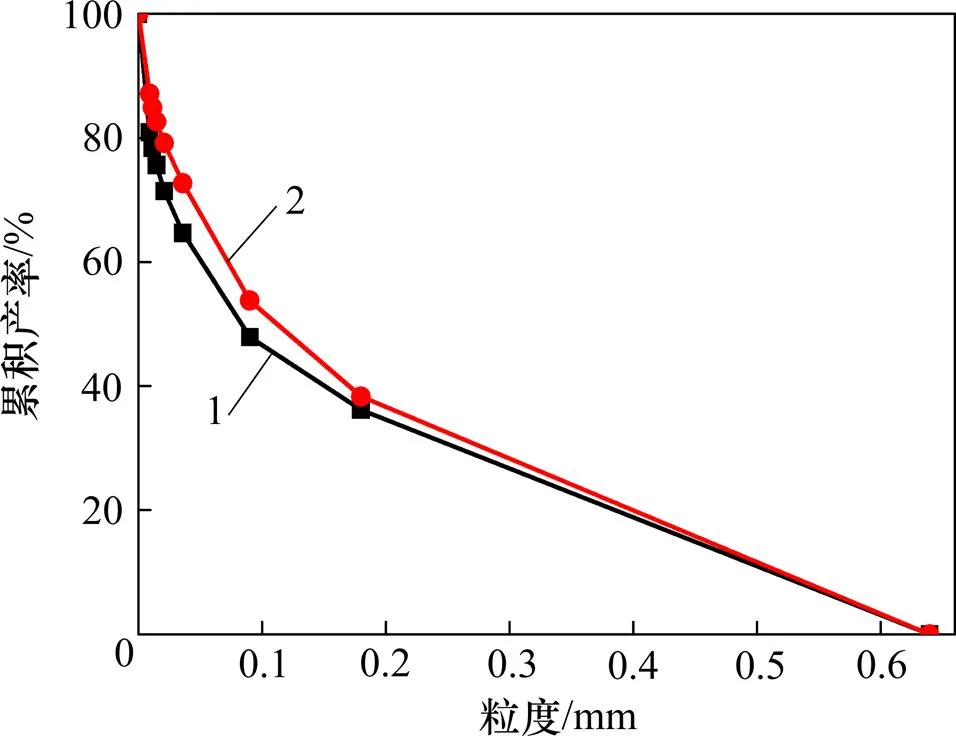
1—高压辊磨；2—颚式破碎

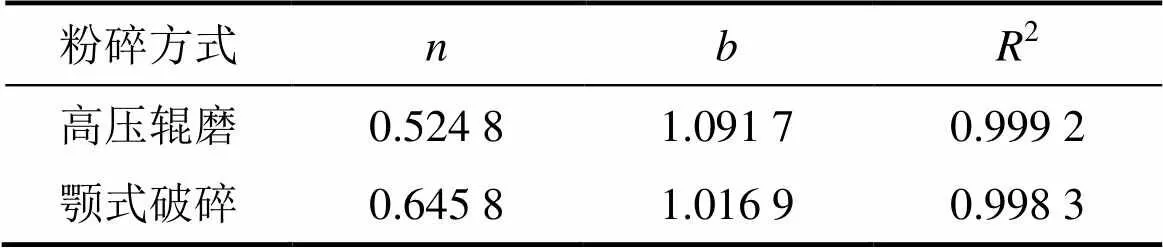
表1 不同粉碎方式下粉碎产品正累积曲线R−R方程回归结果

当＜2.499 mm时，越大，粒度分布越均匀，高压辊磨产品的粒度分布较均匀；当＜1.000 mm时，越小，粒度分布越均匀，高压辊磨产品的粒度分布较均匀；当＞2.673 mm时，越大，粒度分布越均匀，颚式破碎产品的粒度分布较均匀。即颗粒粒度越细，高压辊磨产品的分布越均匀，产率越高，粒度越粗，颚式破碎产品的分布越均匀，产率越高。

高压辊磨产品的粒度分布更均匀，有利于优化粒度组成，使物料处于适合分选的粒度范围，也可避免磨矿时发生粗粒欠磨和细粒过磨现象。

3.2 不同终粉磨条件对邦铺钼铜矿粒度分布的影响

对西藏墨竹工卡邦铺钼铜矿石在V型选粉机转子转速分别为50和200 r/min的条件下进行高压辊终粉磨试验，在终粉磨系统达到稳定时取样。对2种产品进行粒度分析，其正累积粒度特性曲线与R−R方程拟合回归结果分别如图4和表2所示[18]。

由图4和表2可以看出：当转子转速为200 r/min时，得到的产品的粒度比转速为50 r/min时得到的更细，当转子转速为200 r/min时终粉磨产品中粒径小于0.074 mm颗粒的质量分数比转速为50 r/min时的高10.85%，粒度分布更均匀。

转子转速/(r∙min−1): 1—200; 2—50

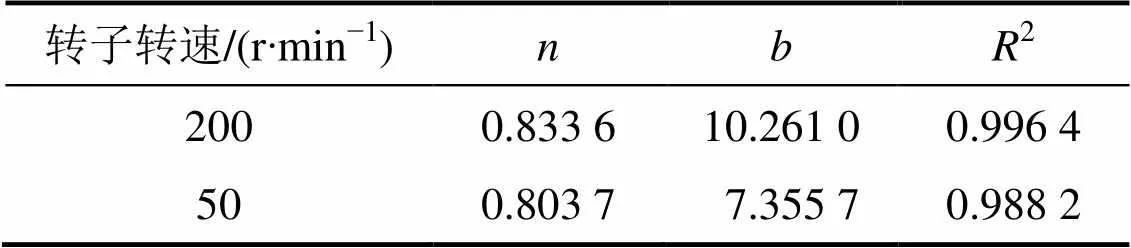
表2 不同转速下粉碎产品正累积曲线R−R方程回归结果

高压辊终粉磨产品在转子转速分别为200和50 r/min时的粒度均小于其相应的粒度特性分界粒度。根据上述分析，越大，粒度分布越均匀，当转速为200 r/min时，产品的粒度分布较均匀。因此，高压辊终粉磨产品在转速为200 r/min时有利于优化粒度组成，使物料处于适合分选的粒度范围。

4 结论

[1] 任中京. 颗粒群粒度均匀性的定量表征[J]. 硅酸盐通报, 1999, 18(3): 12−14. REN Zhongjing. Particle uniformity level expression[J]. Bulletin of the Chinese Ceramic Society, 1999, 18(3): 12−14.

[2] 段希祥. 碎矿与磨矿[M]. 2版. 北京: 冶金工业出版社, 2006: 23. DUAN Xixiang. Crushing and grinding[M]. 2nd ed. Beijing: Metallurgical Industry Press, 2006: 23.

[3] Basim G B, Khalili M. Particle size analysis on wide size distribution powders: Effect of sampling and characterization technique[J]. Advanced Powder Technology, 2015, 26(1): 200−207.

[4] YAO Zhenqiang, GU Weibin, LI Kangmei. Relationship between surface roughness and subsurface crack depth during grinding of optical glass BK7[J]. Journal of Materials Processing Technology, 2012, 212(4): 969−976.

[5] 陈炳辰. 磨矿原理[M]. 北京: 冶金工业出版社, 1989: 318. CHEN Bingchen. Theory of grinding[M]. Beijing: Metallurgical Industry Press, 1989: 318.

[6] Erdemoğlu M, Aydoğan S, Gock E. Effects of intensive grinding on the dissolution of celestite in acidic chloride medium[J]. Minerals Engineering, 2009, 22(1): 14−24.

[7] Schmidt J, Plata M, Tröger S, et al. Production of polymer particles below 5 μm by wet grinding[J]. Powder Technology, 2012, 228: 84−90.

[8] LI Shengyi, WANG Zhuo, WU Yulie. Relationship between subsurface damage and surface roughness of optical materials in grinding and lapping processes[J]. Journal of Materials Processing Technology, 2008, 205(1): 34−41.

[9] Rodríguez B Á, Menéndez-Aguado J M, Coello-Velázquez A, et al. Transient state analysis by simulation in a closed grinding circuit[J]. Minerals Engineering, 2011, 24(5): 473−475.

[10] Bazin C, Obiang P. Should the slurry density in a grinding mill be adjusted as a function of grinding media size?[J]. Minerals Engineering, 2007, 20(8): 810−815.

[11] Fuerstenau D W, Phatak P B, Kapur P C, et al. Simulation of the grinding of coarse/fine (heterogeneous) systems in a ball mill[J]. International Journal of Mineral Processing, 2011, 99(1): 32−38.

[12] 段希祥. 高登粒度特性方程式的参数及变化规律研究[J]. 昆明工学院学报, 1991, 16(2): 15−22. DUAN Xixiang. The research of the parameter and its variable law of Gaudin size degree feature equation[J]. Journal of Kunming Institute of Technology, 1991, 16(2): 15−22.

[13] 段希祥. 球磨机产品粒度特性方程式研究[J]. 昆明工学院学报, 1987, 12(4): 10−20. DUAN Xixiang. The research of particle size equation of the ball-mill products[J]. Journal of Kunming Institute of Technology, 1987, 12(4): 10−20.

[14] 袁致涛, 刘磊, 严洋, 等. 高压辊磨机粉碎贫赤铁矿产品粒度特性[J]. 东北大学学报(自然科学版), 2011, 32(6): 875−878. YUAN Zhitao, LIU Lei, YAN Yang, et al. Product size characteristics of low grade hematite in high pressure grinding roll[J]. Journal of Northeastern University (Natural Science), 2011, 32(6): 875−878.

[15] 袁致涛, 郭小飞, 严洋, 等. 攀西钒钛磁铁矿高压辊磨的产品特性[J]. 东北大学学报(自然科学版), 2012, 33(1): 125−127, 132. YUAN Zhitao, GUO Xiaofei, YAN Yang, et al. Product characteristics of vanadium-titanium magnetite from Panxi by high pressure grinding roller[J]. Journal of Northeastern University (Natural Science), 2012, 33(1): 125−127, 132.

[16] Matijašić G, Kurajica S. Grinding kinetics of amorphous powder obtained by sol–gel process[J]. Powder technology, 2010, 197(3): 165−169.

[17] Ozkan A, Yekeler M, Calkaya M. Kinetics of fine wet grinding of zeolite in a steel ball mill in comparison to dry grinding[J]. International Journal of Mineral Processing, 2009, 90(1): 67−73.

[18] 侯英. 钼铜矿石的高压辊碎磨特性和浮选分离研究[D]. 沈阳: 东北大学资源与土木工程学院, 2014: 40−41, 127. HOU Ying. Crushing behaviour of high pressure grinding rolls and study on flotation separation of molybdenum-copper ore[D]. Shenyang: Northeastern University. School of Resources & Civil Engineering, 2014: 40−41, 127.

(编辑 刘锦伟)

Relationship between parameters of size characteristic and uniformity of particle size distribution

HOU Ying1, YIN Wanzhong2, 3, ZHU Jujian1, YAO Jin3, WANG Yulian3, WU Kai2

(1. School of Mining Engineering, University of Science and Technology Liaoning, Anshan 114051, China;2. School of Zijin Mining, Fuzhou University, Fuzhou 350108, China;3. School of Resources & Civil Engineering, Northeastern University, Shenyang 110004, China)

The parametersandin Rosin−Rammler (R−R) size characteristic equation were studied by analytic geometry and partial derivative method. The analyses include not only the relationship between the parameters and the particle size, but also the effect of parametersandon the particle size distribution. And the conclusion is verified by some examples. The results show thatmainly affects oversized cumulative productivitywhen<>exp(1/). The largeris, and the more uniform particle size distribution becomes. When 0＜＜1 mm, the smalleris, the more uniform particle size distribution becomes. Moreover, the above theoretical results can fully explain the particle size distribution characteristics under different crushing and grinding conditions.

parameters of size characteristic; particle size distribution; size characteristic equation; partial derivative

10.11817/j.issn.1672-7207.2015.09.003

TD952

A

1672−7207(2015)09−3183−05

2014−09−04；

2014−11−29

国家自然科学基金资助项目(51374079) (Project(51374079) supported by the National Natural Science Foundation of China)

印万忠，教授，博士生导师，从事矿物浮选晶体化学原理和难选矿物高效分选技术研究；E-mail: yinwanzhong@163.com