混合动力汽车行星耦合传动系统的图论建模及动力学分析*

杨亚联，米 娇，胡晓松，秦大同

(1.重庆大学，机械传动国家重点实验室，重庆 400030;2.北京理工大学机械与车辆学院，北京 100081)

前言

图论是数学拓扑学的一个重要分支，它在社会科学、自然科学等各领域均有很多应用。文献［1］中以数目合成理论为基础进行自运动链合成行星齿轮系，所得结果虽不完整，但开启了图论理论应用于行星齿轮构造合成与分析的先河，有关行星齿轮系的研究方法甚多，其中以图论方法最具有一般性与系统性。而行星齿轮系由于结构紧凑，易于实现多动力耦合的优点，在混合动力汽车动力传动系统中得到了广泛的应用。

国内学者应用图论对行星齿轮系进行了大量研究，包括行星齿轮的构造合成、运动分析和传动效率分析:其中，文献［2］中将传动方案结构的可行性判别转化为图的平面性判别，从而排除构件干涉的传动简图，这种方法主要针对的是已知传动比，如何确定行星齿轮变速器的传动方案的问题;文献［3］中建立了行星单元体和拓扑单元回路的概念，在图论模型的基础上提出了计算轮系自由度和传动比的方法，主要用于分析行星轮系的传动性能和功率流特性;文献［4］中建立了行星变速机构的图论模型并进行结构几何矛盾判别，通过转换得到构件分析图和转速分析图等，但对于混合动力汽车行星耦合传动方案的设计，该理论还须进一步完善。因此，随着速度耦合传动混合动力系统的应用，如何应用图论理论对混合动力汽车中众多具有行星耦合机构的混合动力传动系统的方案进行建模和分析，成为一个值得继续研究的课题。

本文中基于图论理论，提出了具有行星耦合机构的混合动力系统的整体传动方案的图论模型，根据其邻接矩阵输出邻接码作为有效删除同构方案的判定方法得到混合动力汽车传动系统构型的图论模型，并基于图论理论和图论模型进一步开展混合动力传动系统的运动学和动力学分析，建立了相应的转速和转矩矩阵，为混合动力汽车传动系统的方案设计和分析奠定了理论基础。

1 混合动力汽车行星耦合系统的图论建模

图论的基本原理是研究能够被抽象成为一组点和连接它们的表示特定关系的一组线所构成的图形。所建立的图论模型应具备构件信息、逻辑信息、层次信息和同构信息［3］。混合动力系统是指系统需要多种形式能量或多种动力源搭配工作的系统，在混合动力汽车传动系统中混合动力对应为发动机和电机。为了更好地描述由发动机、电机、动力耦合机构、制动和输出构件构成的复杂混合动力系统，将行星耦合混合动力系统模型的层次信息分为3层:首先，将行星齿轮机构的行星轮放在第Ⅰ层，称为行星层;然后，将与太阳轮共轴回转的其他行星齿轮机构的构件(行星架和齿圈)放在第Ⅱ层，称为太阳层;最后，将输入、输出与制动构件放在第Ⅲ层，称为输入/输出层，见图1。

在建立行星耦合机构的图论模型中，为了更有效地表示基本行星耦合机构的构造关系，以文献［5］中发展的复接头运动链图论表示法为基础，提出行星齿轮系各构件与图论模型的符号转化关系如下:

(1)行星耦合机构各个构件转化为实心圆点;

(2)齿轮副连接转化为虚线连接(若为齿轮内啮合用单箭头虚线表示，若为齿轮外啮合用双箭头虚线表示);

(3)同一回转轴的两个及以上的回转副(即R、H、S共轴回转副)转化为通过点划线连接;

(4)单一回转副(即P与H的回转副)转化为通过双实线连接。

基本行星耦合机构简图转化为其所对应的图论模型如图2所示。在此图论模型的基础上加入输入/输出层，其符号转化关系如下:

(1)输入/输出和制动构件转化为空心圆点;

(2)行星排与输入输出构件的连接关系转化为实线连接;

(3)通过离合器连接的转化为双箭头实线。

根据上述分层结构和构件与符号的转化关系，以丰田公司2004年的Prius混合动力汽车THS-Ⅰ传动系统为例建模，其传动系统构型及对应的图论模型如图3所示。

由于图论模型中构件和线段的符号类型较多，不利于直观快速分析图论模型，提出如下简化方法:(1)将行星排的构件和输入/输出层构件的符号统一为实心圆点;(2)将双实线和点划线统一用实线表示。简化后的图论模型如图4所示。

2 混合动力汽车行星耦合系统图论方案同构判定

在所有图论表述的可能方案中，部分不同构型描述的传动结构在运动学和动力学特性上可能实质是一样的，因此必须对混合动力系统进行同构判定。本文中应用行星排邻接矩阵和构件邻接矩阵的组合来描述混合动力系统的图论模型，通过邻接矩阵输出编码来判断传动系统的同构方案。

2.1 邻接矩阵表示法

邻接矩阵是表示图论中点和线的拓扑关系的有效工具，通过邻接矩阵可以很方便地将图论模型转化为数学模型。首先，以图论模型的行星层和太阳层为研究对象，建立行星耦合机构邻接矩阵A。(1)点i和点j以单一回转副边连接，则aij=1;(2)点i和点j以齿轮副边相连接，内啮合则aij=E，外啮合则aij=F;(3)点i和点j以p个点共用同一回转副连接，则 aij=p;(4)点 i和点 j不连接，则aij=0。

然后以图论模型的太阳层和输入/输出层为研究对象，建立混合动力系统的构件邻接矩阵B。(1)点m和点n以实线连接，则bmn=1;(2)点m和点n以双箭头实线连接即通过离合器连接，则bmn=2;(3)点m和点n不连接，则bmn=0。

以丰田公司Camry混合动力汽车传动系统为例，如图5所示。

根据上述图论模型可得到行星耦合机构的邻接矩阵A和构件邻接矩阵B:

2.2 图论模型的同构判定

对具有行星耦合机构的混合动力系统进行同构判定，首先应确定图论模型各个层次的构件信息，本文中描述的混合动力系统的图论模型的各层构件总数Ni如表1所示。

表1 不同构型图论模型各层次的构件信息

根据各层次的构件数目就可分别确定行星耦合机构和混合动力传动系统的可能方案的数目，再对图论模型进行同构判定，首先根据行星排邻接矩阵A对行星耦合机构进行同构判定，同构是指两图论模型的点与点的邻接关系和点与边的附随关系是完全相同的［6］。是否同构可通过邻接码来判断，由于邻接矩阵A为上三角对称矩阵，因此，取其矩阵上三角的所有数字依序排列的集合作为A的邻接码输出，即由图5的图论模型得到邻接矩阵A即式(1)，输出的邻接码为［55510/555F0/55EE/50F/01/0］，然后按照下述步骤完成行星耦合机构的同构判定。

(1)列举所有可能的位移图形，即为除去行星齿轮图论模型内所有齿轮副对边的不含任何回路的图形;

(2)对每个位移图形合成所有可能的含齿轮回转对的齿轮图形;

(3)删除违反基本行星齿轮系的原则的图形;

(4)由邻接矩阵得到邻接码并进行同构判定;

(5)得到最终的行星齿轮系图论方案并还原为行星齿轮机构图。

以与Camry相同的3自由度双排行星耦合机构为例，对表2所示位移图形进行同构判定可知，2－2和2－3所示图形与2－4的邻接码相同，因此为同构可以删除。对此图论模型得到的不同构最终模型为2－1和2－4，其中2－1即为Camry的行星耦合机构。同理，可以对不同自由度下的不同图论模型的位移图形进行同构判定。

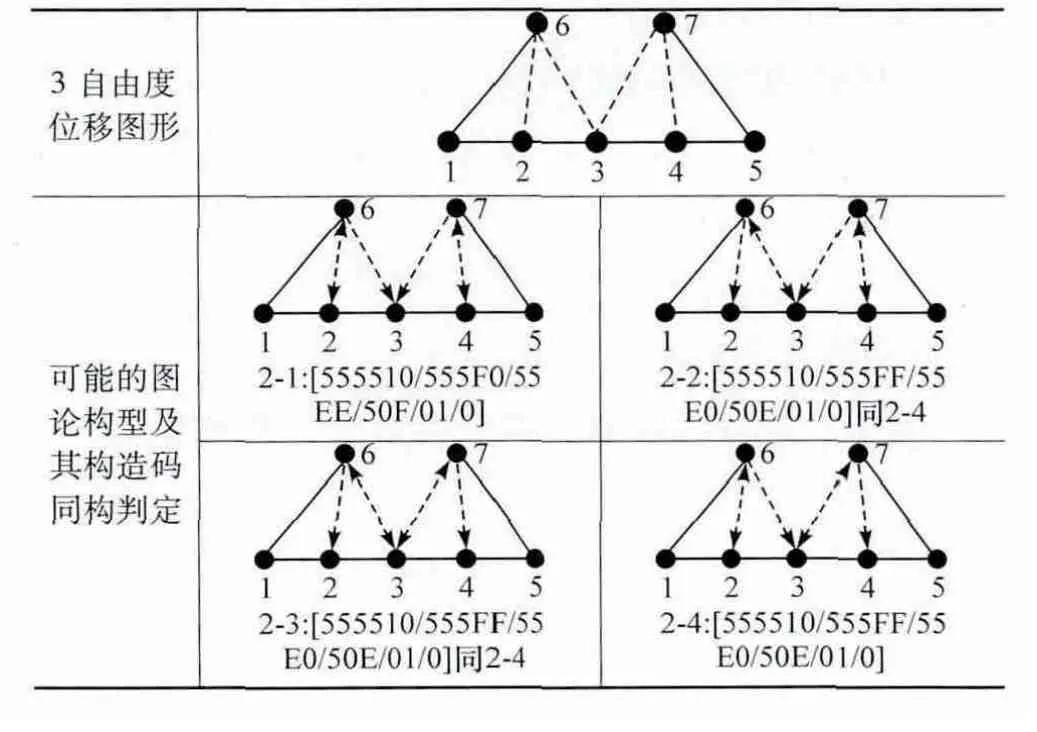
表2 3自由度位移图形的同构判定

然后根据构件邻接矩阵B对混合动力传动系统的可能方案进行同构判定。混合动力系统存在同构方案是由于系统可能存在具有相同性质的构件，例如存在双电机或多个制动器的情况，这时须根据构件邻接矩阵B输出编码来判定同构，取构件邻接矩阵B的性质相同的构件所在行的数字构成集合为B矩阵邻接码，即图5中对应的 B矩阵邻接码为［100000/000100］，若两行数字对换后邻接码相同，则说明这两个构型为同构，则可以删除。

以如图6所示的混合动力系统为例，取B矩阵的MG1和MG2所在行的数字集合构成邻接码B1、B2，B1中两行元素互换后所得的邻接码若与B2相同，说明此两种方案同构可以删除其中之一。

3 混合动力传动系统的运动学与动力学分析

3.1 基于图论的运动学分析

有关行星耦合机构的运动学分析的研究方法有轮系值法［7］、图解法［7］、建表法［8］和基本回路法［9］。基本回路法已成为一种系统的图论理论推导方法。

图论理论的基本回路法主要应用于行星耦合机构的图论模型，因此对于具有单排、双排甚至多排行星耦合机构的混合动力传动系统，只须对传动系统的行星耦合机构的图论模型部分运用基本回路法即可开展运动学分析，由于基本回路法能更方便地得到行星轮的转速与其他齿轮构件的转速关系，因此运用此法也对加入包括行星轮在内的各构件的转动惯量用于动力学分析奠定了很好的基础。

基本回路指的是图论模型中一对齿轮副所对应的点与两对回转副所对应的点构成的三角形封闭回路，如图7所示。结合本文中提出的图论模型可知基本回路具备以下特点:(1)每个基本回路由3个实心圆点、一条实线、一条点划线和一条虚线组成;(2)两个相邻回路都含有属于同一行星耦合机构的行星架和行星轮;(3)每个基本行星耦合机构的基本回路数L必为偶数且等于带箭头的虚线数;(4)行星耦合机构的构件数N与回转副数M的关系为:N=M+1。

以图2的基本行星耦合机构的图论模型的第Ⅰ层和第Ⅱ层为研究对象，可得到单排行星耦合机构的基本回路图，如图7所示。

基本回路由3个基本构件1、2、3组成，其中1和2表示一对啮合齿轮，2和3表示回转副，则可得到该基本回路的转速方程通式为

式中:ω1、ω2、ω3为基本构件 1、2、3 的转速;i12为传动比，i12=±Z2/Z1，±表示齿轮的内啮合或外啮合。

以Prius的单排行星耦合混合动力系统为例，其图论模型如图3所示，结合图7所示的单行星排基本回路的特征可知其行星耦合机构包括两个基本回路(P，S，H)、(P，R，H)，则其基本回路方程为

双排行星耦合混合动力系统以美国通用公司的AHS双模传动系统在低速模式下图论模型为例，如图8所示。其中发动机接第1排行星轮的行星架，电机MG1接第1排行星轮的太阳轮，第1排行星轮系的齿圈和第2排行星轮的太阳轮固联，第2排行星轮的齿圈与机架固联，第2排的太阳轮与电机MG2相连，第2排的行星架输出动力到车轮。

根据上述图论理论可知，双行星耦合机构的基本回路分别为(P1，R1，H1)、(P1，S1，H1)、(P2，R2，H2)、(P2，S2，H2)，根据前述理论推导，可得到基本回路的运动方程组为

同时 ωr1= ωs2= ωmg2，ωs1= ωmg1，ωr2=0，ωh1=ωe，ωh2=ωout，ωs1=ωmg1，联立并整理式(7)可得双排行星耦合机构运动学矩阵:

由式(6)可知两个方程解4个未知量，式(8)有4个方程，解6个未知量，行星排有两个自由度，只要知道两个确定的动力输入转速，则行星排其余所有的转速均可确定，方程组均有解。

3.2 行星耦合混合动力系统的动力学分析

鉴于现有图论理论行星耦合机构的动力学分析中忽略了行星耦合机构各构件的转动惯量，也少有针对整体传动系统的动力学分析，因此本文中在考虑到包含行星轮在内的行星排各构件的转动惯量的前提下，对行星耦合机构进行受力分析。首先，以Prius的THS单排行星耦合混合动力传动系统为例，将图4的图论模型倒置并根据图论的连接关系将各构件的符号一一对应的排列，则可得到如图9所示的图论模型。

将图9的图论模型分别加入行星排各构件和输入输出各构件的转动惯量模块以及受力分析即可得到如图10所示的动力学模型。其中，设Ji为各构件的转动惯量，ri为各齿轮半径，Fi为行星轮与其他齿轮之间的作用力，Ts、Tr、Th为作用在太阳轮、齿圈或行星架上的转矩，设顺时针为正。

取发动机为受力分析主体，有

取MG1电机为受力分析主体，有

取行星耦合机构后的动力传动系统为受力分析主体，有

式中:m整车质量;r为车轮半径;i为行星排至车轮之间的传动比;Tf为车轮阻力矩折算到行星轮系输出端的转矩。Je、Jmg1、Jmg2分别为发动机、电机1和电机 2的惯量;ωe、ωmg1、ωmg2分别为发动机、电机 1和电机2的转速;Te、Tmg1、Tmg2分别为发动机、电机1和电机2的转矩;Ts、Th、Tr分别为单排行星轮系太阳轮、行星架和齿圈上的转矩。

然后取行星轮系进行受力分析，可得THS系统的单排行星耦合机构的动力学方程:

又根据图论连接关系可知:

结合上述各式，最后可得到Prius混合动力传动系统的动力学矩阵:

同理，以图8所示的GM-AHS传动结构为例，将图8转换为图11所示的动力学模型。

取发动机为受力分析主体，有

分别取电机1和电机2为受力分析主体，有

取行星耦合机构后的动力传动系统为受力分析主体，有

取图中第1排行星轮系为受力分析的主体，并进行受力分析，如图12所示。

以行星架为参考坐标系对行星轮进行分析，由达朗伯原理，行星轮要受力平衡，须增加一虚拟的惯性力Fg1有

式中:mp1为行星轮质量;rh1为行星轮旋转中心到行星排旋转中心的距离。选顺时针方向为正，在行星架旋转坐标系上观察行星轮运动:

结合式(19)～式(21)，有

分别以太阳轮、行星架和齿圈为分析对象，有

联立式(23)～式(25)并带入式(21)得

其中 rh1=rp1+rs1=rr1－ rp1，和式(19)、式(22)一起带入式(26)并化简，有

同理，取第2排行星轮系受力分析，有

因行星轮的惯量Jp相对其他行星部件的惯量小，如果忽略行星轮自转的惯量Jp，只考虑折算到行星架上公转的惯量，那么相当于行星架的转动惯量增加了mpr2h，式(27)和式(28)可以进一步简化为

联立式(15)～式(18)、式(29)和式(30)并带入式(31)，得

由式(32)可知，有6个方程解14个变量;结合式(8)，当2自由度行星排系统输入两个确定的输入转速，则其余所有的运动可求，去掉4个转速变量;实际运行的系统，道路阻尼和动力源的功率均为已知，可再消去4个输入输出转矩变量，因此6个方程求解6个转矩变量，式(32)有解。同理，式(14)也有解。上述动力学模型可以完整地描述行星耦合机构和整个传动系统的转速转矩关系。

3 结论

(1)基于图论理论在对行星耦合机构建模的基础上，增加了输入/输出构件层，建立了行星耦合混合动力系统的图论模型。

(2)以Camry行星耦合混合动力系统为例，在行星排邻接矩阵的基础上增加了输入输出构件的构件邻接矩阵，通过邻接矩阵输出邻接码判别传动方案的同构模型，是基于图论理论的混合动力系统方案设计的有效途径。

(3)基于图论理论基本回路法对行星排的运动学分析方法，分别以单排Prius-THS和双排GM-AHS混合动力系统为例，建立了行星耦合混合动力系统的转速分析模型;并考虑行星排转动惯量，进行了行星排的受力分析，推导了行星耦合混合动力传动的动力学转速和转矩模型，为进一步传动方案的性能分析和筛选奠定了基础。

［1］ Johnson R C，Towfigh K．Creat Design of Epicyclic Gear Trains U-sing Number Synthesis［J］．ASME Transactions．Journal of Engineering for Industry，1967:309 －314．

［2］ 邓晓龙，朱大林，方子帆．三自由度串联行星变速箱传动方案设计的图论法［J］．机械传动，2002，26(2):11 －13．

［3］ 薛隆泉，雷亚荣，宋念龙．周转轮系系统化的数学模型［J］．机械工程学报，2008，44(4)．

［4］ 李宏才，闫清东，李慎龙．行星传动方案结构几何矛盾图论判别方法［J］．北京理工大学学报，2010，30(9)．

［5］ Yan H．S，Hsu C．H．Contracted Grahs of Kinematic Chains with Multile Joints［J］．Mathematical and Computer Modelling，1988，10(9):681－695．

［6］ Buchsbaum F，Freudenstein F．Synthesis of Kinematic Structure of Geared Kinematic Chain and Other Mechanisms［J］．Journal of Mechanisms，1970，5(3):357 －392．

［7］ 饶振刚．行星齿轮传动设计［M］．北京:化学工业出版社，2003．

［8］ White G．Multiple-stage，Split-power Transmissions［J］．Journal of Mechanisms，1970，5(4):505 －520．

［9］ Freudenstein F，Yang A T．Kinematics and Statics of a Coupled Spur-gear Train［J］．Mechanism and Machine Theory，1972(7):263－275．

［10］ 秦大同，谢里阳．现代机械设计手册［M］．北京:化学工业出版社，2011．

［11］ Liu Jinming．Modeling，Configuration and Control Optimization of Power-split HEVs［D］．Ann Arbor:Univ．of Michigan，2007．

［12］ Sherman Y T Lang．Graph-theoretic Modelling of Epicyclic Gear Systems［J］．Mechanism and Machine Theory，2005，40:511 －529．

［13］ Roland Mathis A，Yves Remond．Kinematic and Dynamic Simulation of Epicyclic Gear Trains［J］．Mechanism and Machine Theory，2009，44:412 －424．

［14］ 杨亚联，冯荆松．基于图论的行星轮系的运动性分析［J］．重庆理工大学学报，2010，24(7)．