Studies on the key parameters in segmental lining design
Zhenchng Gun,To Deng,Gng Wng,Yujing Jing,c,*
aCollege of Civil Engineering,Fuzhou University,Fuzhou,350108,China
bState Key Laboratory of Mining Disaster Prevention and Control,Shandong University of Science and Technology,Qingdao,266510,China
cDepartment of Civil Engineering,Nagasaki University,Nagasaki,852-8521,Japan
Studies on the key parameters in segmental lining design
Zhenchang Guana,Tao Denga,Gang Wangb,Yujing Jiangb,c,*
aCollege of Civil Engineering,Fuzhou University,Fuzhou,350108,China
bState Key Laboratory of Mining Disaster Prevention and Control,Shandong University of Science and Technology,Qingdao,266510,China
cDepartment of Civil Engineering,Nagasaki University,Nagasaki,852-8521,Japan
A R T I C L EI N F O
Article history:
in revised form
25 August 2015
Accepted 28 August 2015
Available online 10 November 2015
Segmental lining
Uniform ring model
Shell-spring model
Effective ratio of bending rigidity
Transfer ratio of bending moment
A B S T R A C T
The uniform ring model and the shell-spring model for segmental lining design are reviewed in this article.The former is the most promising means to reflect the real behavior of segmental lining,while the latter is the most popular means in practice due to its simplicity.To understand the relationship and the difference between these two models,both of them are applied to the engineering practice of Fuzhou Metro Line I,where the key parameters used in both models are described and compared.The effective ratio of bending rigidityηreflecting the relative stiffness between segmental lining and surrounding ground and the transfer ratio of bending momentξreflecting the relative stiffness between segment and joint,which are two key parameters used in the uniform ring model,are especially emphasized.The reasonable values for these two key parameters are calibrated by comparing the bending moments calculated from both two models.Through case studies,it is concluded that the effective ratio of bending rigidityηincreases significantly with good soil properties,increases slightly with increasing overburden, and decreases slightly with increasing water head.Meanwhile,the transfer ratio of bending momentξ seems to only relate to the properties of segmental lining itself and has a minor relation with the ground conditions.These results could facilitate the design practice for Fuzhou Metro Line I,and could also provide some references to other projects with respect to similar scenarios.
©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by
Elsevier B.V.All rights reserved.
*Corresponding author.Tel.:+86 18753216081.
E-mail address:jiangyjcn@gmail.com(Y.Jiang).
Peer review under responsibility of Institute of Rock and Soil Mechanics, Chinese Academy of Sciences.
1674-7755©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.
http://dx.doi.org/10.1016/j.jrmge.2015.08.008
1.Introduction
The shield-driven tunneling method is widely used for the construction of urban underground tunnels in soft ground due to its advantages of flexibility,effectiveness and minimum impact on the ground surface.Most shield-driven tunnels are supported by segmental lining,which provides the structural capacity to resist the ground and water pressures,as well as the reaction frame to push the shield machine ahead.A certain number of segments are connected by longitudinal joints to form the ring,and then a number of rings are connected bycircumferential joints to form the lining.The configuration of staggered joints,as shown in Fig.1,is commonly used to improve the overall stiffness and minimize the water leakage of segmental lining(Guglielmetti et al.,2007;Maidl et al.,2012).The design of segmental lining is basically carried out by analytical methods or numerical methods,where the lining structure and the loading condition are simplified by designers.
There are generally two models for segmental lining,i.e. indirect-joint model and direct-joint model.The indirect-joint model regards the segmental lining as a ring of uniformity or a ring with multi-hinge,and some corrections are introduced to modify the influence of joints on lining behavior.The direct-joint model regards the segment,the longitudinal joint and the circumferential joint as beam(or shell),rotation spring and shear spring respectively,so that the lining behavior is determined by both segments and joints.On the other hand,there are generally two loading modes imposed by surrounding ground,i.e.activeloading mode and passive-loading mode.The active-loading mode assumes that the surrounding ground applies the earth/water pressures to the lining structure actively,which are calculated by theoretical or empirical formulas.The passive-loading mode takes the ground-lining interaction into account,and the earth/ water pressures transferred to the lining are calculated through the displacement compatibility between ground and lining.
As for the indirect-joint model,the uniform ring model and the multi-hinge ring model are widely used in practice.The former is suitable for the shield-driven tunnel in soft ground,where many practices have been carried out and abundant experiences have been gathered among practitioners.The latter is suitable for the tunneling boring machine(TBM)-driven tunnel in hard rock,where the ground can stabilize itself and provide enough reaction to the lining.Both models introduce some corrections to modify theinfluence of joints on lining behavior equivalently(ITA Working Group No.2,2000;Ding et al.,2004;Koyizumi,2006;Wang, 2010;Gruebl,2012).
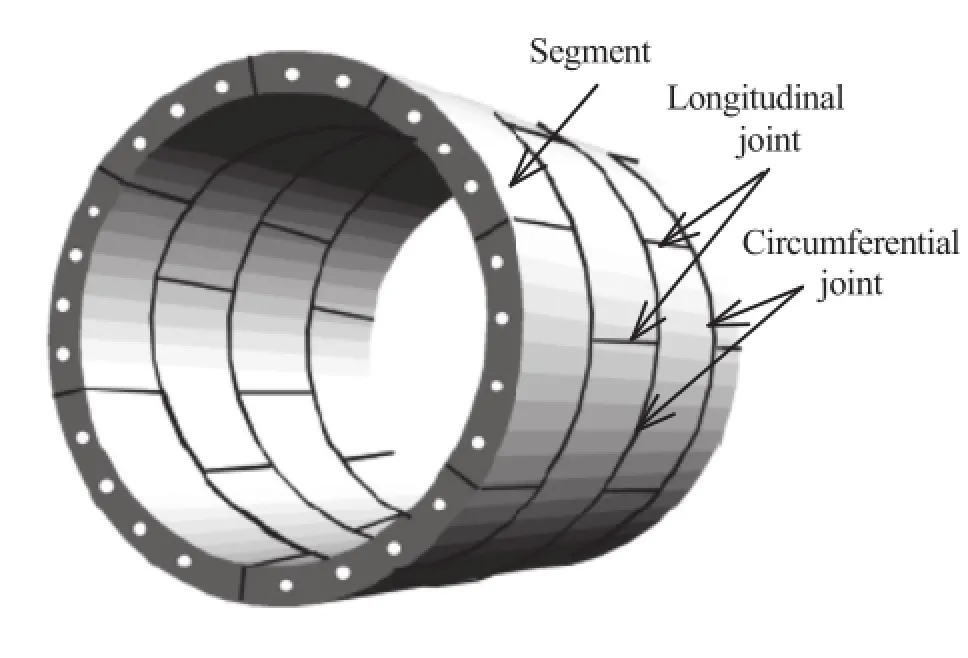
Fig.1.Illustration of segmental tunnel lining.
As for the direct-joint model,the development of large-scale test rig for joint-connected segments and the development of computation capability in finite element analysis make it possible nowtotake the joints intoaccount directly.The beam-springmodel and the shell-spring model are receiving more attraction inpractice nowadays.Many researchers have contributed their work to the following issues:the determination of joint stiffness and the real behavior of segmental lining(Hefny and Chua,2006;Huang et al., 2006;Zhong et al.,2006;Teachavorasinskun and Chub-uppakarn, 2010;Arnau and Molins,2011,2012;Molins and Arnau,2011;Do et al.,2013).
Although both the indirect-joint model and the direct-joint model are commonly used in practice,the relationship and the difference between them are rarely reported in the literature.In this article,the uniform ring model(a typical one based on indirectjoint model and active-loading mode)and the shell-spring model(a typical one based on direct-joint model and passive-loading mode)are thoroughly reviewed in Sections 2 and 3,respectively. Then they are applied to the engineering practice of Fuzhou Metro Line I in Section 4,where the key parameters used in these two models are focused.It is followed by further discussions in Section 5,and finally,some conclusions are summarized in Section 6.
2.Uniform ring model
2.1.Principle of uniform ring model
The uniform ring model regards the segmental lining as a ring of uniformity,and the calculation diagram is illustrated in Fig.2(ITA Working Group No.2,2000;Ding et al.,2004).In this figure,R0and Rcare the radii of extrados line and middle line of uniform ring, respectively;H and Hware the overburdens of soil mass and the water head of groundwater,respectively;p0is the overload on ground surface.
Then the active loads applying on the uniform ring can be calculated by analytical or empirical formulas.The vertical earth pressure equals the total overburden weight or calculated by Terzaghi's formula,as shown in Eq.(1)or(2).Generally speaking,Eq.(2)is employed when the tunnel has a large overburden(i.e.H>(3-4)R0)and the ground condition is good(e.g.stiff clay and dense sand),and Eq.(1)is suitable for other conditions.The vertical water pressure equals the total weight of groundwater above the uniform ring and calculated by Eq.(3).In absence of groundwater,γwcan be set to zero in Eqs.(1)-(3).

Fig.2.Calculation diagram of uniform ring model(after Ding et al.(2004)).

whereγandγware the unit weights of soil and water,respectively;c and φ are the cohesion and internal friction angle of soil mass, respectively.
The horizontal earth pressure is of trapezoidal distribution and can be calculated by
qe1=λpe1,qe2=λ[pe1+2(γ-γw)R0](4)whereλis the coefficient of lateral pressure.
The horizontal water pressure is also of trapezoidal distribution, and can be calculated by Eq.(5)when the ground condition is good(i.e.sand or silty clay),or by Eq.(6)when the ground condition is poor(i.e.clay or mud):
qw1=pw1,qw2=pw1+2γwR0(5)
qw1=λpw1,qw2=λ(pw1+2γwR0)(6)
The horizontal earth resistance is assumed acting triangularly on the uniform ring within the range of±45°,whose maximum magnitude,qr,is estimated by

where khis the coefficient of ground reaction;δis the horizontal deformation of uniform ring;Ecis the elastic modulus of segment;tcis the thickness of segment;ηis the effective ratio of bending rigidity,which is introduced here to consider the decrease of overall bending rigidity caused by longitudinal joints.Notice that the width of segment is set to unity by default in Eq.(7).
The vertical earth resistance,which keeps the uniform ring in kinetic balance,is calculated by the following equation:
pr=pe1+pw1+πtcγc(8)
whereγcis the unit weight of segment.
After determination of the active loadings,the inner forces(i.e. bending moment,hoop force and shear force)of the uniform ring can be calculated by analytical formulas,as listed in Appendix A. However,the longitudinal joint cannot sustain the same bending moment as the segment body does.The calculated bending moment imposed on the longitudinal joint would be transferred in part to the segments of adjacent rings through the shearing mechanism of circumferential joints,as shown in Fig.3.Therefore, the transfer ratio of bending moment,ξ,is introduced here to modify the bending moments carried by segment and joint.
Ms=M0(1+ξ),Mj=M0(1-ξ)(9)
whereM0is the most unfavorablebending moment calculated from the diagram of Fig.2;Msand Mjare the modified bending moments carried by segment and joint,respectively.They are finally used for further design of segment reinforcements and joint bolts.
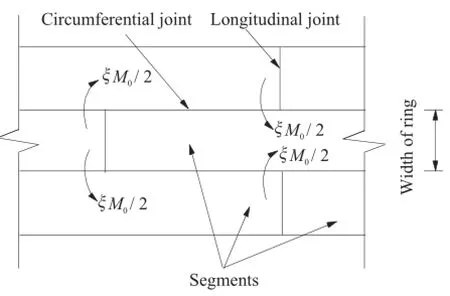
Fig.3.Transferring of bending moment between adjacent rings(after Ding et al.(2004)).
2.2.Parameters used in uniform ring model
The parameters used in the uniform ring model,apart from those geometry parameters,are summarized inTable 1.The ground related parameters can be obtained from laboratory tests(direct shear test and triaxial compression test)and in-situ tests(flat dilatometer test and plate loading test).

Table 1 The parameters used in the uniform ring model and the shell-spring model.
As for the structure related parameters,however,it is difficult to estimate the effective ratio of bending rigidity,η,and the transfer ratio of bending moment,ξ.These two key parameters are not only related to the structure itself but also the ground condition,and areoften estimated empirically in practice.According to Japan's experience(Koyizumi,2006)and China's experience(Wang,2010), ηranges from 0.4 to 0.9 andξfrom 0.3 to 0.6.
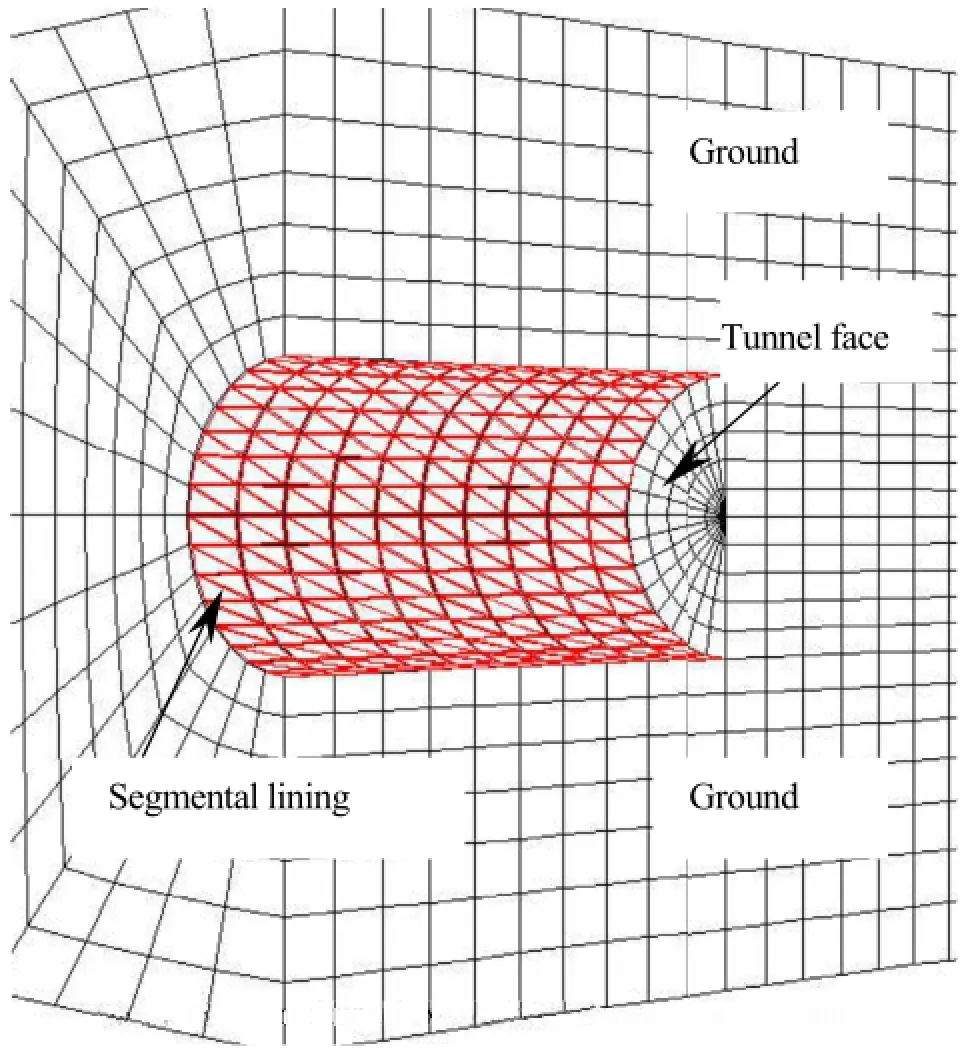
Fig.4.Iteration of tunnel excavation and segment installation.
3.Shell-spring model
3.1.Principle of shell-spring model
The shell-spring model regards the segment,the longitudinal joint and the circumferential joint as shell,rotation spring and shear spring,respectively.The earth/water pressures transferred to the lining are calculated through the displacement compatibility between ground and lining.In this article,the shell-spring model is implementedinthenumericalplatformofFLAC3D(Itasca Consulting Group Inc.,2004)through the following steps.(1)The in-situ stresses under gravitational force are first initialized and the initial displacements of ground are removed.(2)The tunnel is excavated by one ring and the artificial face pressure is applied on the new tunnel face to stabilize the ground.(3)Several segments are attached to the tunnel inner surface one by one,and the joints are set up to connect these newly installed segments.(4)After tunnel excavation and segment installation,the program is marching to new equilibrium.(5)The process presented above is repeated iteratively,as shown in Fig.4,until the whole tunnel is completed.(6)The most unfavorable inner forces at the segments and the joints are extracted for further design of segment reinforcements or joint bolts.
The key technique in numerical simulations is how to deal with the joints adequately.Supposing that three segments are configured staggerly as shown in Fig.5a,these segments are composed of various triangular shell elements,and the shell elements within one segment share the same ID number.
Considering point B,three shell nodes belonging to three different segments coincide at the same position.Two shell nodes belonging to segments 1 and 2 are connected by a node-to-node link as shown in Fig.5b.The link constrains the axial rotation of two nodes by a rotation spring with stiffness of kr,and attaches the other 5 degrees of freedom of two nodes rigidly.The shell node belonging to segment 3 is independent of the other two nodes thoroughly.Consequently,the longitudinal joints are set up to connect several segments into a ring.
Considering point C,two shell nodes belonging to segments 2 and 3 coincide at the same position.They are also connected by a node-to-node link as shown in Fig.5c.The link constrains the radial and the tangential displacements of two nodes by two shear springs with same stiffness of ks,and attaches the other 4 degrees of freedom of two nodes rigidly.Consequently,the circumferential joints are set up to connect several rings into a lining.
3.2.Parameters used in shell-spring model
The parameters used in the shell-spring model,apart from those geometry parameters,are summarized in Table 1.Among the ground related parameters,the elastic modulus,E,and the Poisson's ratio,μ,of soil mass cannot be obtained directly from laboratory or in-situ tests.They can be related to compression modulus, Es,coefficient of lateral pressure,λ,and coefficient of ground reaction,kh,to a certain degree,as presented in Section 4.
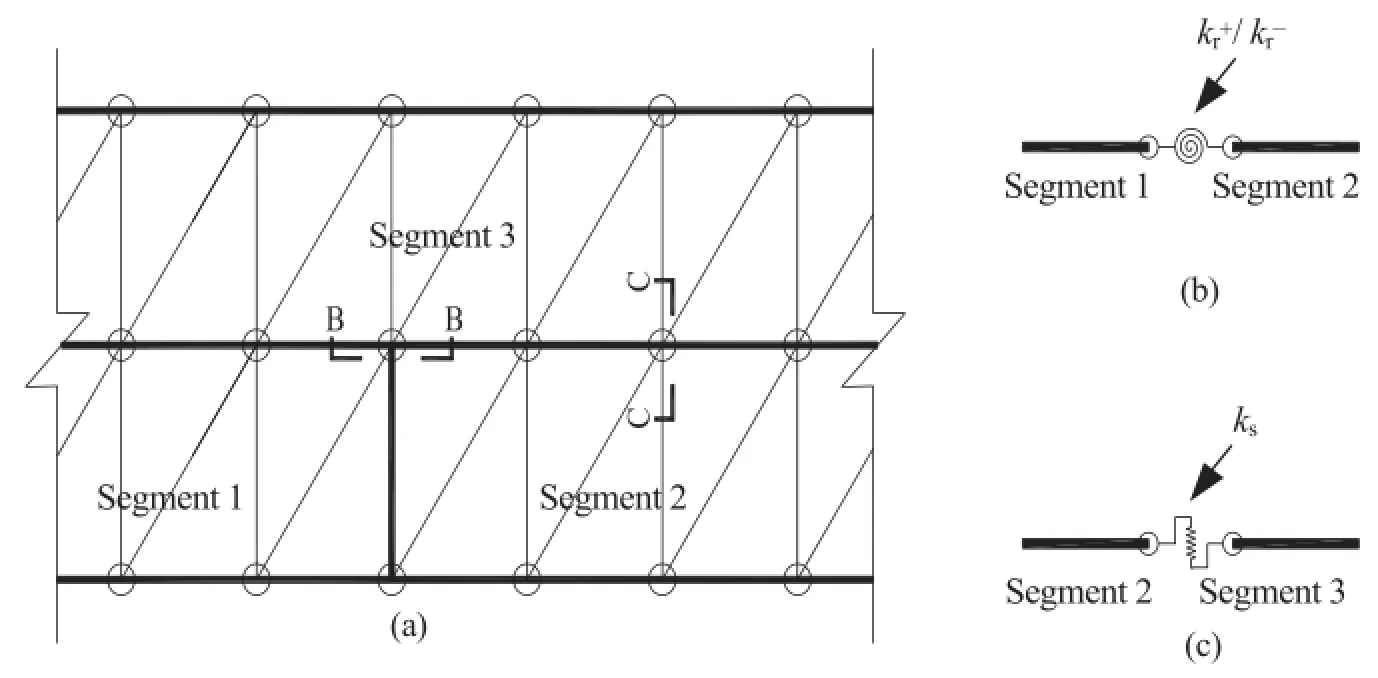
Fig.5.Implementation of joints in numerical simulations:(a)configuration of shells and modes,(b)rotation spring,and(c)shear spring.
As for the structure related parameters,however,it is difficult to determine the stiffness of rotation spring and shear spring.Theyare generally obtained from large-scale bending and shearing tests for joint-connected segments.According to these results(Koyizumi, 2006;Zhong et al.,2006;Do et al.,2013),the behaviors of longitudinal and circumferential joints are simplified as shown in Fig.6.Notice that the longitudinal joint behaves differently when subjected to positive moment(tension in inner side)or negative moment(tension in outer side),thus both the positive rotation stiffness k+rand negative rotation stiffness k-rshould be specified. The positive and negative bending moments of longitudinal joint are limited by Mj+and M-j,respectively.In practice,however,these limits cannot be reached under ordinary scenario,and therefore, they are not taken into account in this article.As for the behavior of circumferential joint,only the shear stiffness ksshould be specified and the limit of shear capacity Sjis neglected for the same reason.
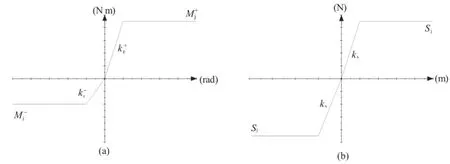
Fig.6.Behaviors of(a)longitudinal joint and(b)circumferential joint.
4.Case studies
Theoretically,the shell-spring model is the most promising means to reflect the real behavior of segmental lining,while the uniform ring model is the most popular means in practice due to its simplicity.They differ in two aspects:(1)The lateral pressure coefficient,λ,and the ground reaction coefficient,kh,are used in the active-loading based uniform ring model,whilst the elastic modulus,E,and Poisson's ratio,μ,of the ground are used in the passive-loading based shell-spring model.(2)The effective ratio of bending rigidity,η,and the transfer ratio of bending moment,ξ,are used in the indirect-joint based uniform ring model;whilst the rotation spring stiffness,k+r/kr,and the shear spring stiffness,ks, are used in the direct-joint based shell-spring model.
These two models are then applied to the engineering practice of Fuzhou Metro Line I.By comparing the response of tunnel lining(mainly the bending moment)calculated from both two models, the relationship and difference between them are carefully studied.
4.1.Outline of Fuzhou Metro Line I(interval tunnel between Baihu Street and Hulu Street)
The Fuzhou Metro Line I,passing through the main urban district of Fuzhou,includes 24 stations and has a total length of 29.2 km.The construction of the metro commenced in July 2010, and will be put into operation in Dec.2015.The interval tunnel between Baihu Streetand Hulu Street,which was completedin Dec. 2014,is focused.It has a length of 1083.4 m,an overburden of 8.9-14.2 m,and a longitudinal gradient of 0.4%-2%.
The typical configuration of segmental lining is illustrated in Fig.7(HECH,2011).The ring with an external diameter of 6.2 m is composed of 1 key segment,2 adjacent segments and 3 standard segments.The segments are made up of C55 reinforced concrete, with impermeabilitygrade of K8.The cross-section of the segments is 0.35 m thick and 1.2 m wide.The properties of the segments are listed in Table 2.Each segment is connected to its neighbors by 2 curved bolts of M30,so that 12 curved bolts are used to form the segment ring.Each segment ring is then connected to its neighbors by 16 curved bolts of M30 every 22.5°along its circumference,so that a certain number of segment rings are installed in sequence to form the segment lining.
According to the geological survey,the ground mainly consists of miscellaneous fill(1_1),mud(3_1),silty clay(4),muddy soil(5_1),silty sand(5_2)and residual clay(7_1),whose properties are listed in Table 3(HECH,2011).Taking the stake XK17+100 for example,the ground condition revealed from boring hole is shown in Fig.8.The tunnel mainly passes through the layer of silty sand(5_2),and the overburden(from the extrados line of tunnel)is about 14 m.Notice that the properties of miscellaneous fill are not provided bygeological survey,and they are assumed to be the same with those of mud(3_1)for simplification.
4.2.The absence of joints
In the absence of joints,the effective ratio of bending rigidityη and the transfer ratio of bending momentξare set to 1 and 0, respectively,in the uniform ring model;the rotation stiffnessand shear stiffness ksare set to be rigid in the shell-spring model. Therefore,the difference related to direct-and indirect-joint models is eliminated,and the difference related to active-and passive-loading modes is focused in this section.The equivalent elastic moduli and Poisson's ratios of soil masses,which are unavailable from geological survey,correspond to the lateral pressure coefficients and ground reaction coefficients of soil masses.
4.2.1.Uniform ring model
In the absence of joints,the effective ratio of bending rigidityη and transfer ratio of bending momentξare set to 1 and 0, respectively.The parameters used are listed in Tables 2 and 3,and the bending moment along the perimeter of uniform rigidity lining is shown as the red line in Fig.9.
Due to the unavailability of the elastic modulus,E,and Poisson's ratio,μ,of soil masses in geological survey,the equivalent elastic modulus and Poisson's ratio for each layer of soil mass should be determined as follows.The elastic modulus for a certain layer of soil mass is assumed to increase linearly with the overburden H,by the proportion of the ground reaction coefficient,kh,but limited by five times of compression modulus,Es(Chang and Zhang,2007):
E=Es+khH≤5Es(10)
4.2.2.Shell-spring model
The shell-spring model is implemented in the numerical platform of FLAC3D.The triangular shell element in the numericalsimulations has a width of 0.6 m(corresponding to one half of segment width),a length of 0.579 m(corresponding to one eighteenth of tunnel circumference)and a thickness of 0.35 m.Each ring consists of 128 triangular shell elements;totaling 18 rings are established in the numerical simulations to form a segmental lining of 21.6 m long.The properties of shell element are listed in Table 2. Both the stiffness of rotation spring krand the stiffness of shear spring ksare set to be rigid in the absence of joints,so that the socalled segmental lining is identical to the uniform lining.In summary,there are 2053 shell nodes,2304 shell elements and 596 node-to-node links in the numerical simulations.
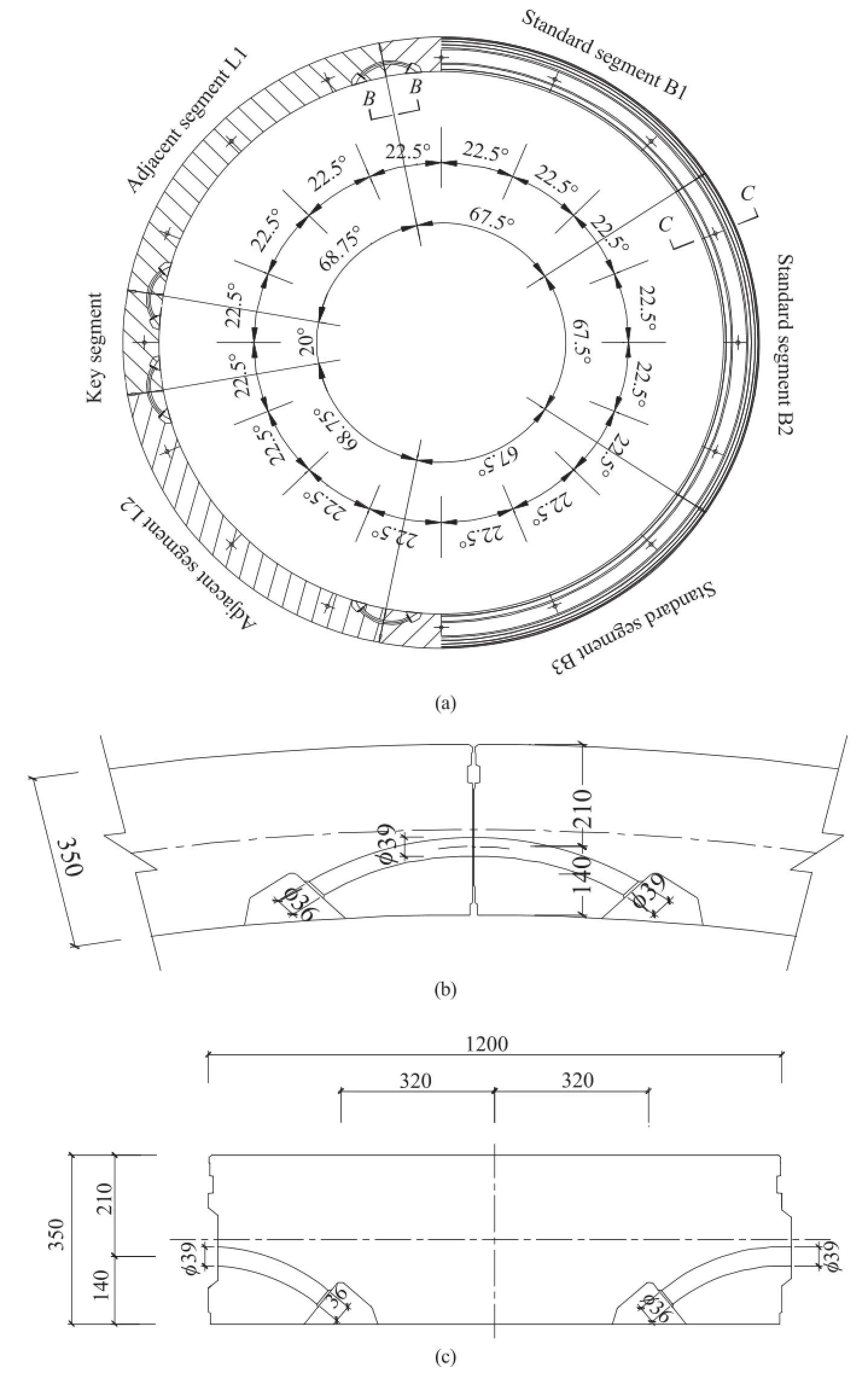
Fig.7.Design details of segmental lining in Fuzhou Metro Line I:(a)general configuration,(b)details of longitudinal joint,and(c)details of circumferential joint(unit:mm).

Table 2 The properties of segments.
The surrounding ground included in the numerical simulations consists of 5 soil layers as shown in Fig.8,which has a total width of 60 m,a total length of 21.8 m(corresponding to 18 rings alongtunnel axis)and a total depth of 50 m.The Mohr-Coulomb constitutive model is assumed for the soils and their properties are listed in Table 3.The depth of residual clay(7_1)is assumed to reach the bottom of numerical model for simplification.The ground is simulated by the hexahedron zones with 8 nodes,and there are totally 30,528 zones and 32,523 nodes included in the numerical simulations.The water table is set to 2.5 m from the surface,so that the water head(from the extrados line of tunnel)is about 11.5 m. The nodes of segmental lining are coupled with those of soil mass, so that the soil-structure interaction can be significantly simplified. The artificial pressure applied on the excavation face is referred to the earth pressure monitored in soil chamber during construction, which is set to 300 kPa at the stake XK17+100.

Table 3 The properties of soil masses.
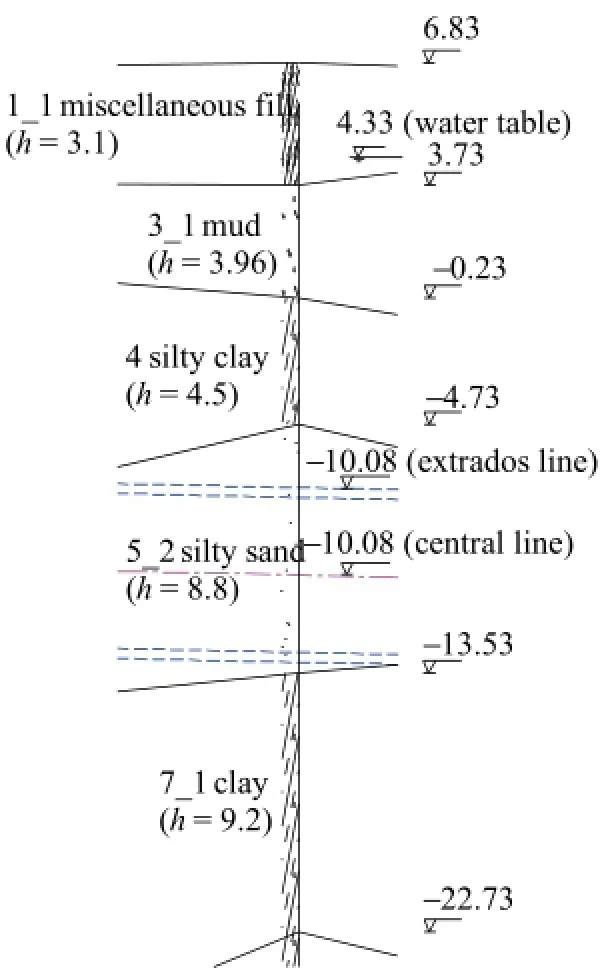
Fig.8.Ground condition revealed from boring hole at the stake XK17+100(unit:m).

Fig.9.Bending moment along the perimeter of uniform and segmental linings(in the absence of joints).
The Poisson's ratio of a certain layer of soil mass is considered by the empirical values.When the Poisson's ratios of mud,silty clay, silty sand and residual clay are set to 0.43,0.38,0.33 and 0.35, respectively,the bending moment calculated by the shell spring model is extracted and depicted as the blue line in Fig.9.The bending moments calculated from these two models fit each other well,which implies that the equivalent elastic moduli and Poisson's ratios of soil masses are feasible.
4.3.The presence of joints
In the presence of joints,the equivalent elastic moduli and Poisson's ratios of soil masses used in the previous section are employed in this section.Therefore,the difference related to activeor passive-loading mode is eliminated,and the difference related to direct-or indirect-joint model is focused.The reasonable effective ratio of bending rigidityηand transfer ratio of bending momentξ, which are generally estimated by designers'experience,correspond to the rotation stiffness and shear stiffness of joints. 4.3.1.Shell-spring model
In the presence of joints,the shell-spring model is implemented by the same numerical simulations as described above,but with the rotation stiffnessof 10,000/4000 kN m/rad and the shear stiffness ksof 50,000 kN/m(see details in Appendix B).The joint configurationsof9oddringsand9evenringsareillustratedinFig.10. The totaling 18 rings are established to form a segmental lining of 21.6 m long.The bending moment calculated by the shell-spring model is extracted and depicted in Fig.11,where the bending moment along the perimeter of segmental lining decreases globally, especially at the positions of joints(denoted by arrows in Fig.11).

Fig.10.Joint configuration of segment lining:(a)odd ring,and(b)even ring.
Taking the odd ring for example,the maximum and minimum moments carried bysegment(denoted asand,respectively) are 92 kN m(at standard segment B2)and-100 kN m(at standard segment B1),respectively;the maximum and minimum moments

Fig.11.Bending moment along the perimeter of segmental lining(in the presence of joint).
4.3.2.Uniform ring model
In the presence of joint,the parameterηis introduced to consider the overall decrease of bending rigidity.The uniform ring model is applied to the same engineering practice,with the effective ratio of bending rigidityηsetting to 0.9,0.7,0.5,0.3 and 0.1, respectively.The bending moments along the perimeter of uniform lining are shown in Fig.12,and the maximum and minimum moments of uniform rigidity lining are denoted as
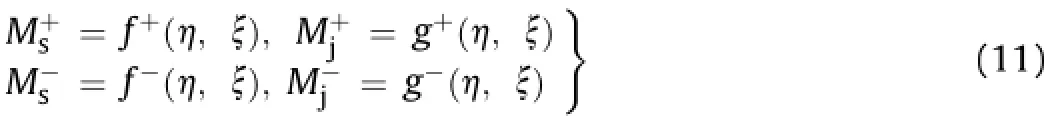
4.3.3.Selection of effective ratio of bending rigidity,η,and transfer ratio of bending moment,ξ
The purpose of this section is to select the reasonable values of parametersηandξ,so that the bending moment calculated by the uniform ring model could approximate the real response of segmental lining calculated by the shell-spring model.The procedure consists of the following two steps.

Fig.12.Bending moment along the perimeter of uniform lining(in the presence of joints).
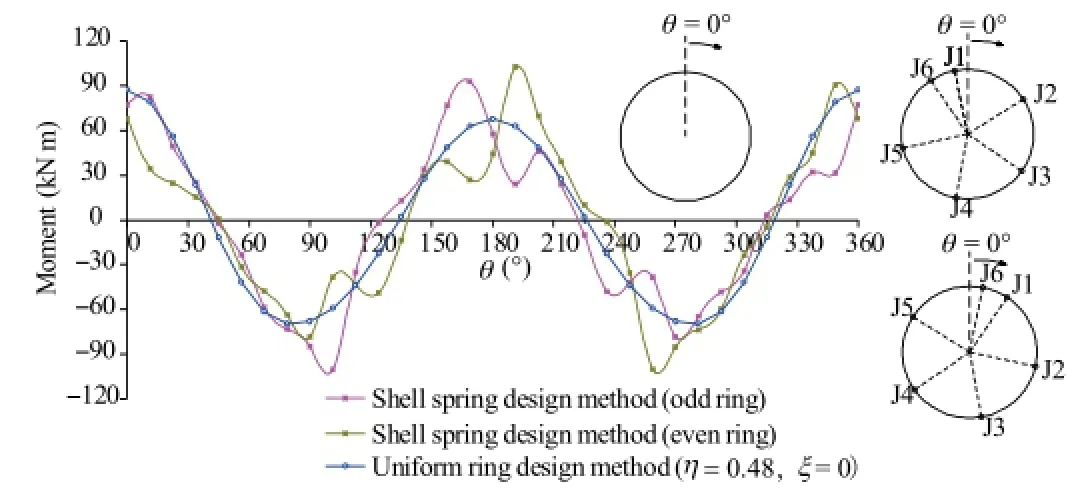
Fig.13.Selection of effective ratio of bending rigidity,η,and transfer ratio of bending moment,ξ.
The value for the effective ratio of bending rigidityηshould be determined firstly.Many possible values of parameterηare tried(while the parameterξis set to zero here),so that the bending moments along uniform lining(Fig.12)generally fit those in segment lining(Fig.11).Whenηis set to 0.48,for example,the bending momentalong uniform lining isdepictedand shown as the blue line in Fig.13,whereandare 88 kN m and-70 kN m, respectively.For comparison,the bending moment calculated by the shell-spring model is also shown in this figure.
Based on the result obtained from the first step,the reasonable value for transfer ratio of bending rigidity,ξ,can be determined in the second step,which artificially modifies the maximum/minimum bending moments imposed by segment and joint according to Eq.(9).Many possible values of the parameterξare also tried(while the parameterηremains constant here),so that the modified maximum/minimum bending moments in uniform lining(Eq.(11))could approximate the counterparts in segment lining=97 kN m,=-99 kN m,=33 kN m,=-38 kN m). Whenξis set to 0.45,for example,andare 127 kN m and-102 kN m,whileandare 48 kN m and-38 kN m, respectively.They are slightly greater than their counterparts in segment lining,which implies that the parameter combination of η=0.48 andξ=0.45 is reasonable.
It is noticed that other combinations of parametersηandξcould also be employed,due to the designer's attitude towards risk of safety in tunnel design.The principle suggested in this article is that the modified maximum/minimum bending moments in uniform lining should be slightly greater than those in segment lining,due to the conservative attitude towards risk of safety in tunnel design.
5.Discussions
To understand the influence of groundconditions onselection of parametersηandξ,another 14 cases with different overburdens, soil properties and water heads are studied,as listed in Tables 4 and 5.
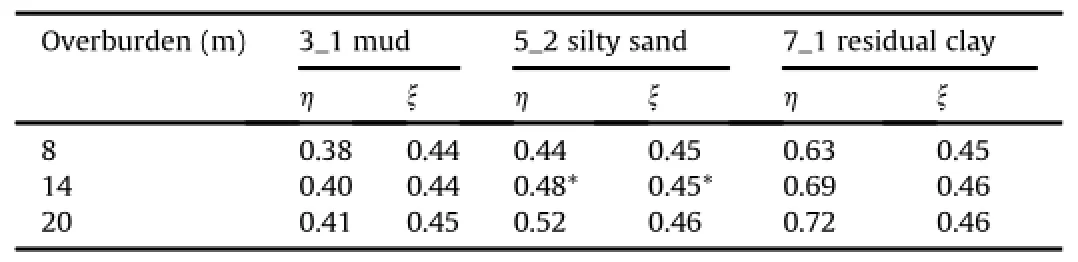
Table 4 Selection ofηandξdue to different overburdens and soil properties(water head=11.5 m).

Table 5 Selectionofηandξduetodifferentwaterheadsandsoilproperties(overburden=14 m).
In Table 4,it is assumed that the tunnel passes through the soil layer of mud(3_1)and residual clay(7_1),respectively.In numerical simulations,the properties of the silty sand(4)are replaced by those of mud(3_1)and residual clay(7_1),respectively(see Fig.8 and Table 3),while other ground conditions remain unchanged.For the 1st and 3rd cases in Table 4,the overburden of tunnel is assumed to be 8 m and 20 m,respectively.In numerical simulations,the depths of miscellaneous fill(1_1)and silty clay(4)decrease(or increase)by 3 m,while other ground conditions remain unchanged.For each case,the reasonable combination of parametersηandξis determined by the similar procedure presented above and then listed in Table 4.
InTable 5,the tunnel is assumed to pass through the soil layer of mud(3_1)and residual clay(7_1),respectively.For the 2nd and 3rd cases inTable 5,the waterhead of tunnel(from tunnel extrados line to water table)is assumed to be 5.7 m and 0 m,respectively.For each case,the reasonable combination of parametersηandξis determined by similar procedure presented above and then listed in Table 5.
The effective ratio of bending rigidityη,which reflects the relative stiffness between segmental lining and surrounding ground,should assume a larger value when the ground could provide sufficient constrain upon the segmental lining.Therefore,it increases significantly with good soil properties,increases slightly with the increasing overburden and decreases slightly with the increasing water head.The transfer ratio of bending momentξ, which reflects the relative stiffness between segment and joint, seems to remain constant in all cases.It implies that the parameter ξonly concerns with the properties of segment lining itself(e.g. joint configuration,joint stiffness)and has a minor relation with ground conditions.
6.Conclusions
The uniform ring model and the shell-spring model for segmental lining design are reviewed in this article,where the parameters used in both models are described and compared.To understand the relationship and the difference between these two models,they are applied to the engineering practice of Fuzhou Metro Line I through the following two procedures.(1)In the absence of joints,the difference related to direct-and indirect-joint models is minor.The equivalent elastic moduli and Poisson's ratios of soil masses can be determined by comparing the bending moment calculated from the spring-shell model with those from the uniform ring model.(2)In the presence of joints,the difference related to direct-and indirect-joints is evident.The reasonable values for effective ratio of bending rigidity and transfer ratio of bending moment can be determined by comparing the bending moment calculated from the uniform ring model with those from the shell-spring model.
Furthermore,to understand the influence of ground conditions on selection of parametersηandξ,another 14 cases with different soil properties,overburdens and water heads are carefully studied. It is concluded that the effective ratio of bending rigidity increases significantly with good soil properties,increases slightly with the increasing cover depth and decreases slightly with the increasing water head.Meanwhile,the transfer ratio of bending moment seems to only relate to the properties of segment lining itself and has a minor relation with the ground conditions.
The uniform ring model has been widely used in the design practice of shield-driven round tunnel in soft ground due to its simplicity.By selecting the reasonable values of parametersηandξ, the inner forces(mainly the bending moment)calculated from uniform ring model could approximate the real structure responses of segment lining.These results could facilitate the design practice for Fuzhou Metro Line I,and could also provide some references to other projects with respect to similar scenarios.
Conflict of interest
The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.
Acknowledgment
The research is sponsored by the Natural Science Foundation of China(Grant No.51008082),which is gratefully acknowledged.
Appendix A.Bending moment along the perimeter of uniform ring
The following analytical formulas are referred to ITA Working Group No.2(2000)and Ding et al.(2004).
Due to vertical earth and water pressures(pe1+pw1),we have
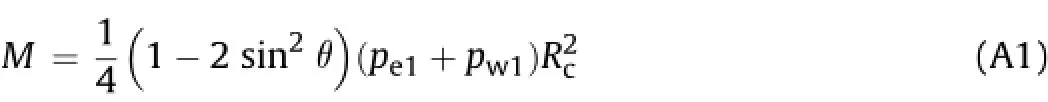
Due to horizontal earth and water pressures(qe1+qw1),we have

Due to horizontal earth and water pressures(qe2+qw2-qe1-qw1),we have

Due to weight of segment lining(g1),we have

Due to horizontal resistance(qr),we have
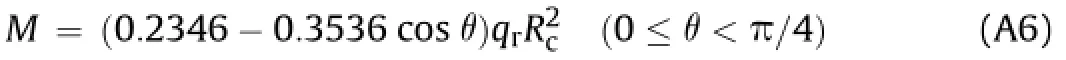

Appendix B.Determination of joint stiffness
The stiffness of longitudinal joint is obtained by the bending experiments of jointed segment.Many Japanese researchers and corporations have carried out experiments for different types of segments and joints.These experimental results are summarized by Koyizumi(2006),which are partially listed in Table A1.Also Koyizumi(2006)has proposeda theoretical formula toestimate the stiffness of longitudinal joint,which is more complex and not included here.
Referring to these experimental results,the stiffness of longitudinal joint in Fuzhou Metro Line I(Rc×bc×tc=6200 mm× 1200 mm×350 mm,2 curve bolts in 1 row with steel plate)is roughly set to 30,000 kN m/rad.In this article,each longitudinal joint consists of three rotation springs,thus the positive stiffness of

Table A1 The stiffness of longitudinal joint in the reinforced concrete segment(after Koyizumi(2006)).
The stiffness of circumferential joint could be obtained by largescale shearing experiments on segmental lining.Among limited experimental results,Koyizumi(2006)suggested that the stiffness of circumferential joint is about 80-1000 MN/m.In numerical simulations,adjacent segmental rings are connected through 16 node-to-node links(i.e.16 curved bolts in circumferential joint). Thus,the stiffness of each shear spring ksis set to 50,000 kN/m in this article,which corresponds to the total stiffness of circumferential joint about 80 MN/m.
References
Arnau O,Molins C.Experimental and analytical study of the structural response of segmental tunnel linings based on an in situ loading test.Part 2:numerical simulation.Tunnelling and Underground Space Technology 2011;26(6):778-88.
Arnau O,Molins C.Three dimensional structure response of segmental tunnel linings.Engineering Structures 2012;44:210-21.
Chang S,Zhang S.Handbook for engineering geology.Beijing:China Architecture and Building Press;2007(in Chinese).
Ding W,Yue Z,Tham L,Zhu H,Lee C,Hashimoto T.Analysis of shield tunnel.International Journal for Numerical and Analytical Methods in Geomechanics 2004;28(1):57-91.
Do N,Dias D,Oreste P,Djeran-Maigre I.2D numerical investigation of segmental tunnelliningbehavior.TunnellingandUndergroundSpaceTechnology 2013;37:115-27.
Gruebl F.Segmental ring design:new challenges with high tunnel diameter.Muir Wood Lecture of International Tunnelling Association(ITA);2012.http://www. ita-aites.org/en/publications/muir-wood-lecture.
Guglielmetti V,Grasso P,Mahtab A,Xu S.Mechanized tunnelling in urban areas:design methodology and construction control.London:Taylor&Francis;2007.
Hefny A,Chua H.An investigation into the behaviour of jointed tunnel lining. Tunnelling and Underground Space Technology 2006;21(3-4):428.
Huadong Engineering Corporation of HydroChina(HECH).Design documents of Fuzhou Metro Line I contract section No.2.HECH;2011(in Chinese).
Huang Z,Zhu W,Liang J,Lin J,Jia R.Three dimensional numerical modelling of shieldtunnellining.TunnellingandUndergroundSpaceTechnology 2006;21(3-4):434.
ITA Working Group No.2.Guidelines for the design of shield tunnel lining. Tunnelling and Underground Space Technology 2000;15(3):303-31.
Itasca Consulting Group Inc.User manual of fast Lagrange analysis of continua in 3 dimensions,version 3.0.Minneapolis,USA:Itasca Consulting Group Inc.;2004. Koyizumi J.Segment design from allowable stress method to limit state method. Tokyo:Japan Society of Civil Engineering;2006(in Japanese).
Maidl B,Herrenknecht M,Maidl U,Wehrmeyer G.Mechanised shield tunnelling. Berlin:Ernst&Sohn;2012.
Molins C,Arnau O.Experimental and analytical study of the structural response of segmental tunnel linings based on an in situ loading test.Part 1:test configurationandexecution.TunnellingandUndergroundSpaceTechnology 2011;26(6):764-77.
Teachavorasinskun S,Chub-uppakarn T.Influence of segmental joints on tunnel lining.Tunnelling and Underground Space Technology 2010;25(4):490-4.
Wang M.Tunnelling and underground engineering technology in China.Beijing:China Communications Press;2010(in Chinese).
Zhong X,Zhu W,Huang Z,Han Y.Effect of joint structure on joint stiffness for shield tunnel lining.Tunnelling and Underground Space Technology 2006;21(3-4):406-7.

Dr.Zhenchang Guan is associate professor in Fuzhou University.His research interests cover the construction and maintenance of tunnels,especially the mountain tunnels excavated by NATM and the urban tunnels driven by shield.To date,Dr.Guan has published more than 20 journal papers.Dr.Guan also has participated 3 research projects that are funded by the National Natural Science Foundation of China and Ministry of Education of China.
15 December 2014
 Journal of Rock Mechanics and Geotechnical Engineering2015年6期
Journal of Rock Mechanics and Geotechnical Engineering2015年6期
- Journal of Rock Mechanics and Geotechnical Engineering的其它文章
- Characterizing the influence of stress-induced microcracks on the laboratory strength and fracture development in brittle rocks using a finite-discrete element method-micro discrete fracture network FDEM-μDFN approach
- Effects of fracture distribution and length scale on the equivalent continuum elastic compliance of fractured rock masses
- Shear strength behavior of geotextile/geomembrane interfaces Belén M.Bacasa,*,Jorge Cañizalb,Heinz Konietzkyc
- Engineering properties for high kitchen waste content municipal solid waste
- Effects of spatial variation in cohesion over the concrete-rock interface on dam sliding stability
- Evaluation of the effect of sodium silicate addition to mine backfill, Gelfill-Part 2:Effects of mixing time and curing temperature
