井筒与油藏耦合数值模拟技术现状与发展趋势

高大鹏　王　东　胡永乐

（1.中国石油勘探开发研究院，北京　100083； 2.北京大学地球与空间科学学院，北京　100871；3.中国石化胜利油田采油工艺研究院，山东东营　257000）

井筒与油藏耦合数值模拟技术现状与发展趋势

高大鹏1，2王东3胡永乐1

（1.中国石油勘探开发研究院，北京100083； 2.北京大学地球与空间科学学院，北京100871；3.中国石化胜利油田采油工艺研究院，山东东营257000）

从井流量方程、井筒内热多相管流计算、多段井模型和近井区域加密的扩展井模型等4个方面总结了井筒与油藏耦合数值模拟技术的研究进展，指出目前存在的主要问题包括：复杂结构井流量方程中参数取值误差很大，不能提供准确的源汇项；高含水阶段井筒内多相管流非常复杂，常用的计算流体力学模型误差很大；非等温井筒内流固耦合模拟机理认识不清楚，数值计算时间长；模拟多层合采时未考虑纵向非均质性，薄差油层的动用情况与实际不符。提出了基于多相管流计算的多段井模型与油藏耦合的数值模拟技术、扩展井模型与油藏耦合的数值模拟技术、考虑井筒出砂和结蜡等复杂现象的流固耦合数值模拟技术是未来的发展趋势。

油藏数值模拟；多相管流计算；多段井模型；扩展井模型；流固耦合

长期以来，油藏数值模拟作为油气田开发过程中一项可信赖的技术，在油藏工程师做大型决策、评价油藏以及诊断和改善油藏产能时发挥了不可替代的作用。油藏数值模拟中任何井模型的基本目的都是提供准确的源汇项。近年来，随着中国水驱陆相油田开始普遍进入高含水和高采出程度的“双特高”开发阶段，特低渗、低产、低丰度、高黏度边际油田的开发逐步得到重视，井眼轨迹和井身结构复杂以及安装了井下监测和调控设备的水平井和多分支井成为现阶段老油田挖潜增产和新油田经济开发的重要技术。

传统油藏数值模拟中的井模型是一个源汇项，采用固定的井底流压或产量作为内边界条件，忽略了井筒内的流体流动过程以及压力变化，模拟精度对于需要利用油藏数值模拟技术寻找剩余油的老油田而言还远远不够，因此有必要发展井筒与油藏耦合数值模拟技术，其主要目的在于：（1）准确模拟多分支井各分支的流动；（2）准确描述垂直、水平井筒内的热多相流动；（3）解释由于摩擦、静水力、加速度和滑移造成的各相之间的速度差与沿程压力损失；（4）模拟井下流量控制设备。

1　不断完善的井流量方程是广泛应用于井筒模拟的简化模型

由于井生产监测资料和井筒管流模型的限制，经常不考虑井筒内的多相管流，通过建立井的流量方程简单表征产量或注入量与井底流压、地层压力、井段长度以及压裂裂缝导流能力等参数之间的关系，并将流量方程作为内边界条件进行油藏数值模拟。目前直井的流量方程已经非常成熟，研究热点主要集中在多段压裂水平井和复杂结构井。

1.1多段压裂水平井流量方程

近年来国内外学者采用保角变换、镜像反映、压降叠加和等值渗流阻力等方法推导了大量多段压裂水平井解析流量方程，根据假设的地层流体到井筒的不同渗流过程，将多段压裂水平井流量方程分为3类。第1类是仅考虑地层径向流和裂缝内线性流两部分的多段压裂水平井流量方程，Guo等［1］（1997年）考虑沿裂缝的压力降和流量变化，提出了贯穿多条垂直压裂缝的水平井流量方程，相比于前人假设无限导流能力和均匀流裂缝推导的流量方程更为准确。第2类是进一步细分地层流体到压裂水平井的渗流过程后，Guo等［2］（2008年）在Wei等［3］（2005年）的研究基础上，将地层线性流、径向流和裂缝线性流、径向流进行耦合，提出了相应的水平井流量方程。第3类是Yuan等［4］（2010年）分别考虑从裂缝到井筒和从地层到井筒两部分流动，提出了压裂水平井流量方程，与前两类流量方程的区别在于假设地层内有流体可以直接流入井筒，之前的假设均认为地层内的流体需要先流入裂缝，再从裂缝流入井筒。为了将水平井流量方程转化为井模型引入油藏数值模拟中，Wan等［5］（2002年）将多段压裂水平井半解析流量方程求解的井底流压与网格压力相结合，计算了模拟所需的井指数。这些多段压裂水平井流量方程存在很多局限：（1）均考虑的是垂直裂缝，而实际上在浅部地层还可能出现水平裂缝，对于裂缝的形态做了很多简化；（2）将多相渗流问题简化为均质单相渗流。应用流量方程虽可对多段压裂水平井的产能进行简单预测，但是当地层、完井和压裂等情况复杂时误差很大。

1.2复杂结构井流量方程

复杂结构井主要包括3种。第1种是水平方向仅有一个井段并且井眼轨迹呈蛇曲状延伸的波状井，常用于贯穿多个独立的含油气地质体。Kankom［6-7］（2007年）通过对水平井流量方程进行修正，使之可用于大斜度井、波状井等。第2种是分支井段在同一层位内且各分支之间存在渗流干扰的多分支井。程林松［8］（1995年）综合运用数学方法和物理模拟方法推导了多分支井流量方程，Salas等［9］（1996年）的流量方程中进一步考虑了表皮因数的影响，Wolfsteiner等［10］（2000年）考虑地层的非均质性，推导了多分支井流量方程，王晓冬（2006年）［11］则是在水平井当量井径模型的基础上基于压降叠加原理建立了多分支井流量方程。第3种是分支井段在纵向上交错位于不同油层内且不考虑渗流干扰的多分支井，可将不同的分支段作为独立的水平井段，进而采用水平井流量方程计算各分支段的流量，然后再进行叠加得到多分支井的流量方程。上述多分支井流量方程均只考虑单相渗流，与实际情况差距较大，Guo等［12］（2007年）利用提出的多分支井组分流量方程，计算了每个分支内各组分的流量，至此多分支井的流量方程趋于成熟。

1.3井流量方程中参数取值误差很大，不能提供准确的源汇项

现有生产动静态资料提供的参数不足以模拟井筒内的管流时，采用井的流量方程作为数值模拟中的源汇项，虽然这种方法对于直井较为常用且获得了较高的精度，但对于处理复杂结构井还存在很多局限：（1）饱和度梯度导致油、气和水相的相对渗透率在井与井所在网格块内有所不同，井内的绝对有效渗透率与网格块内的渗透率平均值不同；（2）传统商业模拟器如Eclipse和CMG等采用等效网格块半径来计算直井的井指数，而对于复杂结构井，等效网格块半径是一个错误的等效处理；另外，传统商业模拟器中其他的假设条件和参数取值也更适合直井而不是复杂结构井；（3）传统商业模拟器中采用有效表皮因数来表征井周围的污染程度，但它是一个未知的变量，模拟将其作为假设的常量严重影响了流量方程的计算精度，由于井产量、气油比和水油比均对流量方程非常敏感，因此流量方程参数取值的误差将严重影响复杂结构井的模拟精度。

2　井筒热多相管流计算是井筒与油藏耦合数值模拟的基础

多相流体在井筒和多孔介质中的流动有本质上的不同，需要分别采用不同的模拟方程和数值求解方法。井筒内的管流与常规管流不同之处在于井壁上会有流体的流入或者流出，这将影响井筒内的流体流型、流体摩擦和加速度压力损失。特别是对于水平井、波状井和多分支井等复杂结构井，它们在储层内的完井段更长，井筒内多相管流也更为复杂，对于井产能的影响也越来越无法忽略。

2.1考虑油气水三相井筒管流的耦合数值模拟技术

井筒管流作为流体力学的重要部分，通常与油藏渗流的研究相互独立，为了将两部分流体流动相互耦合进而对油井产能做出更为准确的预测，在水平井方面，程林松［13］（2002年）在黑油模型的基础上，建立了考虑水平井井筒压力损失（包括摩擦、加速度、混合和重力压力损失）的非均质油藏数值模拟模型。在多分支井方面，Ouyang［14-15］（1998年、2001年）首先提出了多分支井单相井筒管流与油藏渗流耦合的数值模拟模型，该模型能够确定任意时间油井产能、井指数、井筒压力剖面以及流入流出量分布。在此基础上，Chen等［16］（2000年）采用Beggs-Brill关系和Ouyang均匀模型计算了井壁流入流出、加速度和流型的影响，进而提出了考虑油水两相管流的多分支井的产能模型。

上述模型选择了不同的井筒水力计算模型建立井筒与油藏耦合数值模拟模型，分别适用于水平井两相管流、多分支井单相管流和两相管流，井筒与油藏耦合模拟的整体思路一脉相承。在此基础上，研究更为复杂的长井筒内三相管流问题成为建立更加精确的井筒与油藏耦合数值模拟的关键。Shi［17-18］（2005年）通过实验得到的三相稳态漂移流动模型成为了井筒多相管流的理论基础，在此基础上，Krogstad［19］（2007年）考虑多相流体滑移效应，提出了井筒管流与油藏渗流耦合的模型，在后来的井筒数值模拟研究中被广泛应用。

2.2考虑井筒内复杂现象的耦合数值模拟技术

实际生产过程中，井筒内可能存在非牛顿流体、水力压裂、井筒储存效应、窜流和油挥发等特殊现象，需要对已经建立的三相管流模型进行改进。（1）采取水平井多段压裂技术增产后，井筒内的流动受压裂工艺的影响很大，为此，Vicente［20］（2006年）提出了地层渗流与多段压裂水平井筒管流相互耦合的全隐式数值模型；（2）非牛顿流体在井筒内的流动与达西流体存在很大差别，王明等［21］（2006年）通过计算分支井开采稠油时井筒内压力降落，建立了多分支井幂律流体渗流的数值模拟模型；（3）试井过程中开关井时的井筒储存效应、窜流等对产能影响很大，为此Hu［22］（2007年）对三相井筒管流模型中流体相态属性进行改进，采用隐式方法耦合井筒管流模型和油藏渗流模型，对关井和开井时的井筒储存效应、气举套管管头和井筒内窜流等现象进行了模拟；（4）开发挥发性油藏时，挥发油对井筒管流影响明显，而前人提出的模型不能准确模拟挥发油，为此Shirdel等（2009年）［23］对井筒与油藏耦合组分模拟器进行了改进。

2.3考虑井筒内热多相流动的耦合数值模拟技术

计算流体力学（CFD）软件近年来发展迅速，主要是基于欧拉双流体模型，采用多流体体积方法来分析各种流体流动机制，研究井筒内的压力降落以及物质、热量交换，比较常用的是FLUENT CFD软件。例如，Zeboudj［24］（2010年）将CFD首次应用于模拟水平井以不同方式射孔完井时井筒内的流体流动。Yuan［25］（2014年）将CFD应用于模拟高压高温井的相流速、压力和温度分布。近年来，CFD软件已经趋于成熟，在井筒管流中的应用也越来越广泛，但CFD主要适用于直井和水平井，对于复杂结构井和安装有井下设备的情况应用较少，并且CFD主要应用于单口井筒内热多相管流计算，还没有很好地嵌入大型油藏数值模拟器。为此，Livescu［26］（2010年）将提出的热多相井筒管流模型与斯坦福的通用油藏模拟器GPRS对接，通过将井筒和油藏内的物质平衡方程、能量守恒方程以及压力降落进行耦合，开展井筒与油藏耦合数值模拟计算。

2.4高含水阶段井筒内多相管流非常复杂，常用的CFD模型计算误差很大

目前常用的CFD模型可以较好的应用于水平井筒多相管流计算，但在高含水阶段井筒内的油和水组成了一种具有明显不同混合流速的乳状液，CFD模型不能准确模拟这种现象：（1）模型中的很多参数不够准确，如上部和底部边界处气泡的大小、界面规律以及多相之间的物质交换等；（2）高含水阶段井筒内不同流型之间的转换机理认识还不清楚，在CFD模型中无法准确模拟不同流型之间的转换；（3）CFD模型适用于计算直井和水平井井筒内的管流，在复杂结构井中应用较少；（4）CFD模型在考虑井筒内存在井下设备时模拟不够准确，然而国内高含水多层油藏普遍采用精细分层注水技术，井筒内管流模拟的难度非常大。

2.5非等温井筒内流固耦合模拟机理认识不清楚，数值计算时间长

油井生产过程中井筒内形成沥青质或蜡沉淀的时间和机理还没有认识清楚，普遍认为压力、温度和组分的变化都可能是导致这些沉淀的原因。特别是流体流经流量控制设备后可能会出现严重的压力下降，此时温度也会出现变化进而加剧沥青质或蜡沉淀。Thanyamanta［27］（2007年）基于尚不成熟的理论，提出了组分和非等温效应相结合的流动模型，用以预测油井中的沥青质沉淀；Trina［28］（2012年）通过将油藏稳态三相非等温渗流模型与油管内压力、温度、流速和持液率剖面的计算模型、蜡沉淀模型三者相互耦合，提出了模拟蜡沉淀过程的油藏数值模拟模型。这两个模型的关键在于模拟了井筒内的温度分布，因而增加了大量的能量守恒方程，在进行多井区块综合数值模拟时都需要耗费大量的时间。

在模拟蒸汽辅助重力泄油（SAGD）开采沥青或稠油时，通常一个蒸汽室对应一口注蒸汽井和一口生产井，一个SAGD作业点覆盖附近几对井。从数值模拟的角度来看，SAGD作业开始时蒸汽室彼此独立，模拟可以在单一的SAGD井对上执行。随着加热和泄油过程的进行，由于压力连通、汽窜和水层间的相互影响，每一对井不再保持独立，那么模型中的网格数量将会迅速增加，甚至达到几百万个，除了预测各相的流动特征以外，还需要对蒸汽室内的压力和温度变化进行模拟，传统的商业软件将花费很多的时间来模拟，为此很多学者在求解方法上做了许多改进，例如罗海山等［29-30］（2011年）根据温度、各相饱和度随空间变化的快慢在不同区域采用不同尺度网格，提出双孔双渗模型下的自适应网格算法及裂缝基质方程的解耦方法。此外，许多大的石油技术服务公司已经投入了大量精力开发新一代模拟工具［31］。

3　多段井模型是油藏数值模拟中处理复杂井筒的关键

多段井模型将复杂结构井处理为节点与管的网络系统，如图1所示。传统井模型将井视为一个流体组分均一的混合整体，反映的是向井流动的整体状态，多段井模型克服了这种近似处理方法带来的误差，可以在每一分支井段内产生不同的混合流体，此外还能够灵活处理各种类型的井，也能处理不同类型的向井流动控制设备、封隔器和环空流等情况。

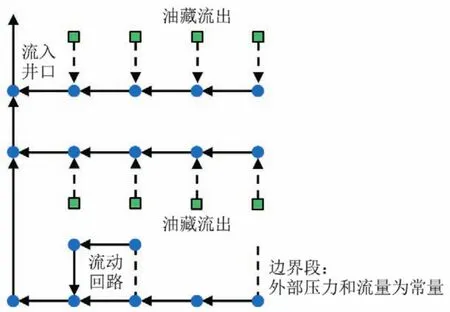
图1　多段井模型

3.1多段井模型的发展历程和主要特点

多段井模型由Holmes［32］（1998年）首次提出并用以模拟复杂结构井，模型中的井筒被划分为任意多段，段数越多模拟精度越高。之后许多学者在此基础上进行了诸多改进，如Stone［33］（2001年）将多段井模型应用于组分模拟器，提出了基于多段井模型的热模拟方法，每段的主要变量包括段压力、总体摩尔流速、各组分摩尔体积和每段体积的内能。Semenova等［34］（2010年）考虑复杂结构井和储层内的各流体之间的热交换、滑移效应造成的流体持液率和摩擦压力损失，提出了能够计算复杂井的压力和温度剖面的多段井模型，该模型优势在于能够应用均质或者滑移流动模型确定井中各相的分布。至此多段井模型已经趋于成熟，Holmes［35］（2010年）结合前人的研究成果，认为先进的多段井模型具有以下几个特点：（1）可以在井段网络中任意位置的井段设置压力限制，而不仅是在井底段；（2）井段的节点和管作为独立的项来处理，进而可以灵活地模拟许多井下装置；（3）该模型还可模拟井筒内的热交换和非达西流。近年来，多段井模型又在模拟井下节流控制设备、水力压裂方面体现出了不可替代的优势。例如Edwards［36］（2013年）将多段井模型应用于水力压裂的模拟中，将裂缝作为井模型的一部分，一个平面裂缝由多段井相互连接的分支构成的网来模拟，如图2所示，其主要的优势在于：（1）裂缝网独立于储层模拟网格，因而模型的建立更加容易；（2）模拟过程中可以任意增加或改变裂缝；（3）裂缝可与网格线以任意角度相交；（4）裂缝几何形态及属性表征更加全面。

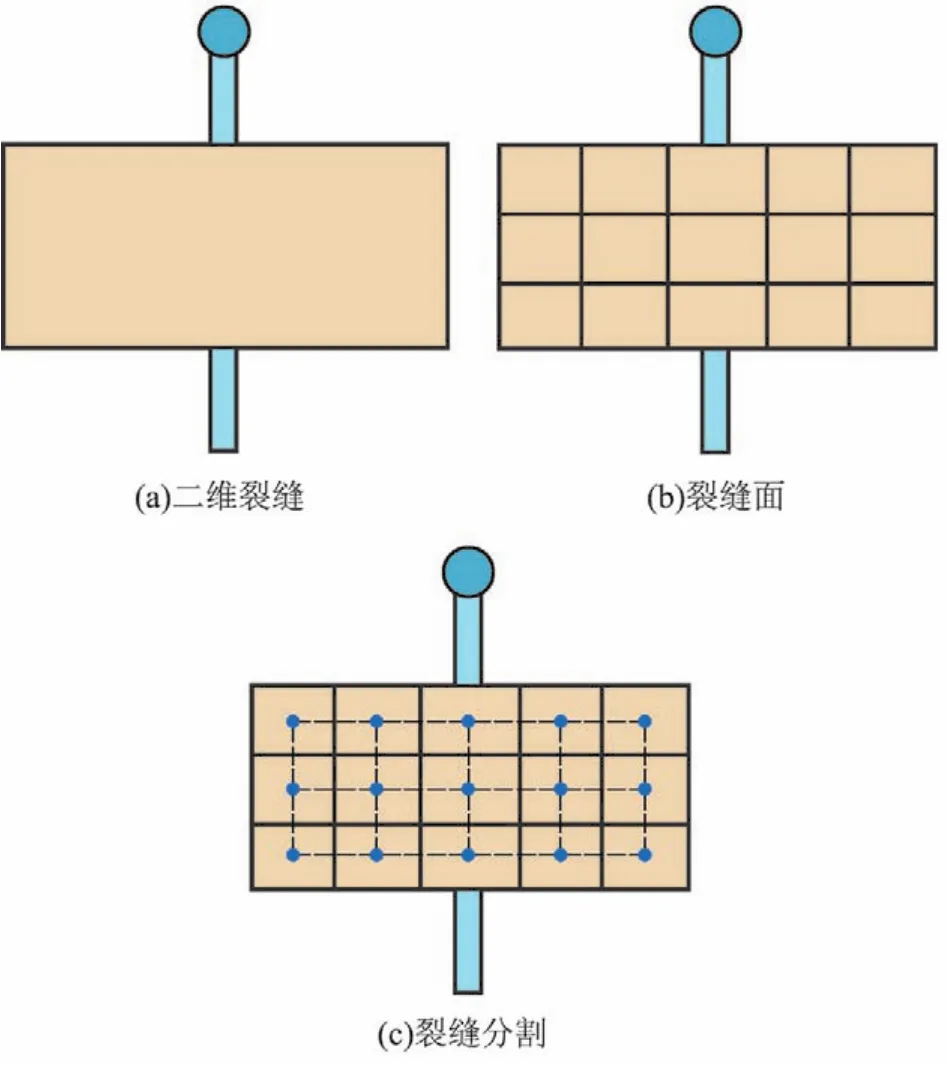
图2　多段井模型表征裂缝示意图

3.2多段井模型在模拟带有井下设备的井筒时发挥了巨大作用

采用复杂结构井开发多层油藏时，通常会在井筒内安装井下流量控制设备（ICD），用于阻碍高速流体的循环流动。油藏中的流体进入环空后经过ICD进入油管内，会在油管和地层之间产生一个额外的压降，能够使整个井筒内的压力降落更为均衡，阻碍高速渗流层的流体流出，有助于形成一个均衡的生产或者注入剖面。长期以来，油藏数值模拟中忽略了ICD的影响，导致无法准确拟合各个层段的剩余油分布。

为了准确模拟井下流量控制设备的影响，Neylon［37］（2009年）首先对多段井模型进行改进，允许一个井段存在任意数量的出口，提出了能够形成环形流动路径的多段井模型，环空中流体可以被封隔器堵塞，也可以流经多个ICD（图3），进而研究了考虑环空内流体流动和不考虑环空内流体流动的多段井模型（图4）。在此基础上，Youngs［38］（2009年）提出了两个封隔器之间有多个ICD存在时的多段井模型（图5），至此利用多段井模型模拟带有井下设备的井筒已经非常成熟。

除了利用多段井模型之外，Zarea等［39］（2011年）、赵国忠等［40］（2012年）也分别针对研究的具体问题提出了考虑井下节流控制设备的多分支井产能模型和油藏数值模拟方法，但是模拟精度与多段井模型相比差距很大。国内许多高含水油田采用精细分层注水工艺提高油层动用程度，其复杂且智能化的管柱结构对于油藏数值模拟来说是一个挑战，因此非常有必要发展多段井模型的研究。

图3　环空内带有封隔器和不带有封隔器的流动

图4　多段井表征全封隔环空内有流动和无流动示意图

图5　封隔器内有多个流量控制设备的情况

3.3模拟多层合采时未考虑纵向非均质性，薄差油层动用情况与实际不符

多层油藏中薄差储层已经成为老油田挖潜增产的重要对象，然而传统商业模拟器在模拟多层合采时射开的油层均被动用，这与实际情况明显不符。造成这种现象的原因是传统商业模拟器将渗透率很低的薄差油层内的流动仍视为达西流，而室内实验发现可能存在启动压力梯度等非达西现象，因此多层合采时低渗透油层处的内边界条件应当考虑非达西渗流，这对模拟的精度影响很大，特别对于剩余油相对分散的开发时间长的国内多层砂岩油田，准确拟合薄差油层的开采历史是找到剩余油的关键。

例如在对特高含水阶段的大庆长垣杏树岗油田进行油藏数值模拟时，采用传统商业模拟器历史拟合后纵向上各个小层的开采状况误差很大，原本取心分析剩余油储量很大的二类表外储层模拟时却被强水洗，主要原因是井在模拟器中的处理误差很大，低渗表外储层未考虑非达西渗流现象。

3.4基于多相管流计算的多段井模型与油藏耦合的数值模拟是未来的发展趋势

多段井模型能够更细致地表征井筒及环空内的多相管流，通过设置合理的段和节点来计算井筒及环空内不同位置的温度、压力、流态和组分构成，传统的多段井模型主要采用垂直流动性能来简单表征油管中的流动，忽略了井中的流动动态。如果将多相管流模型与多段井模型进行耦合，不仅是对先进管流模型的延续，更可以充分发挥多段井模型的优势，然后将其作为油藏渗流方程的内边界条件进行求解，更准确的说明摩擦、滑移和窜流等引起的压力损失和井筒与油藏之间的热交换。此外，不同的完井方式对井附近储层内的渗流也有很大影响，如射孔数目、位置等，并且采用精细分层注水技术开发时井筒内封隔器和水嘴等井下节流设备也有很大影响，因而建立与多相管流模型耦合的多段井模型可以更精确地模拟井筒和油藏内的流体流动和能量交换。例如Sagen［41］（2011年）建立的油藏、井筒与运输管线三者耦合模型，实现了从地下到地面的系统模拟，成为新一代耦合模拟器的一次尝试。

4　扩展井模型和流固耦合为油藏数值模拟的发展提供了新思路

传统的油藏数值模拟概念中将整个模型分为井筒和油藏两部分，而扩展井模型中分为井区域和油藏区域，如图6所示，井区域与井模型的井筒相比还增加了部分近井储层，这个区域内岩石的非均质性（包括裂缝和近井储层损害等）都对井产能有直接影响，并且由于高流速和强压力梯度导致岩石压缩效应、相变和非达西渗流现象在近井区域内更为严重。扩展井模型可以更为精确地模拟这些复杂的近井现象，井区域内网格的形状、大小和精度根据等压面的情况以及要求的模拟精度来确定。

图6　扩展井模型示意图

在模拟水力压裂井时，近井瞬时效应和复杂相变特征的影响非常严重，如果模拟过程中近井模型的边界条件不实时发生改变，将导致多相流的模拟出现错误的结果。Karimi-Fard［42］（2011年）利用瞬时生产指数与近井网格加密相结合的方法来更新油藏模型，提出了人工压裂井的模拟方法。在此基础上，Ding［43］（2011年）提出了一种新的近井流动模型与油藏渗流模型相互耦合的模拟技术，核心在于不断更新各相的生产指数乘子，通过近井模型的边界条件和油藏模型的生产指数实时更新及互换实现耦合模拟。该技术在研究多层油藏中的钻井引发的储层损害以及水平井堵水方面效果较好。该模型的缺点在于：井生产指数作为重要的耦合模拟衔接参数，对于有贯穿多个网格的长裂缝井来说，采用单一的井生产指数不能表征井与油藏的全部接触情况，对于低渗储层中长时间的瞬时流动机制也无法表征。为了弥补这些缺陷，Karimi-Fard［44］（2011年）进一步提出了基于非结构化网格加密技术研究近井效应的高分辨率模型，Nakashima等［45］（2012年）又提出了可以应用于三相黑油模型的近井多相流加密方法，Li等［46］（2013年）又将近井多相流加密技术应用于重油初次开发的粗尺度模拟。总体来看，虽然现阶段扩展井模型应用较为局限，但提供了一种精确模拟复杂近井现象的新思路。

4.1基于扩展井模型的油藏数值模拟是未来考虑复杂近井现象的主流技术

随着对储层认识精度的不断提高和开发井网的不断完善，井附近区域出现的复杂现象也越来越受到重视，同时越来越多的复杂结构井应用于开发低渗透、稠油和复杂断块等难采油田，为此有必要将扩展井模型应用于复杂结构井，使之能够研究井附近区域出现的非达西流、储层污染和凝析油分离等复杂现象。扩展井模型是一种较为新颖的数值模拟技术，可以根据油藏实际情况自动划分井区域内的网格，并且随着计算机处理能力的大幅度提高，也促使井区域内的网格越来越细，模拟精度和效率都有了较大提高。

4.2考虑井筒出砂、结蜡等复杂现象的流固耦合数值模拟也是未来发展的关键

关于井的流固耦合数值模拟包括井筒与井筒内流体的耦合、井周围动态裂缝生长繁殖、流体内混合固体颗粒后的流动等，这几种复杂的流固耦合数值模拟都是当前研究的热点。例如在研究砂岩油藏油井出砂现象时，需要结合对出砂机理的认识，综合考虑混有砂粒的流体在地层中渗流、经过环空内防砂设备的流动以及井筒中管流三个过程进行模拟，进而建立出砂定量预测模型，这对于控制地层出砂、选择合理的防砂设备具有实际意义。此外，油气生产过程中沥青质沉淀和结蜡也是个重要问题，它们如何以及何时开始沉淀还不明确，开发过程中压力、温度和组分的变化都是主要诱发因素。流体流经安装在管柱上的多种类型的流量控制设备可能会导致严重的压力下降，在这些情况下温度会出现变化，可能会析出沥青质沉淀或者结蜡，因此也需要深入研究关于井的流固耦合数值模拟。

5　结论

（1）在资料受限或者不考虑井筒内多相管流时可以采用复杂结构井流量方程作为油藏数值模拟的内边界条件，但随着对于井筒多相管流认识的不断深入和管流计算模型精度的不断提高，复杂结构井数值模拟开始向多段井模型、热多相管流模型与油藏模型耦合计算的方向发展。

（2）井筒与油藏的耦合模拟已在多个领域中成为热点，比较成熟的研究成果集中于各种井流量方程、考虑井筒管流的单井产能模型、复杂结构井多段井模型和简单的扩展井模型等方面，发展趋势则主要集中在对特殊情况的模拟，如安装了井下设备、井筒出砂、结蜡和析出沥青质等等，总体来看是倾向于流固耦合数值模拟方面，目前尚缺乏一个能够广泛适用的流固耦合模拟软件。

（3）先进的井模型需要能够适应复杂的井轨迹，并且能够模拟不同的井筒情况，多段井模型是井筒与油藏耦合数值模拟的有力支撑，然而由于多段井模型与油藏模型耦合求解过程中增加了大量的方程和未知数，并且近井区域加密和流固耦合又增加了整个求解系统的复杂性，因此需要更快更稳定的求解方法。

［1］GUO B, SCHECHTER D S. A simple and rigorous mathematical model for estimating inflow model for a horizontal well［R］. SPE 38104, 1997.

［2］GUO Boyun, YU Xiance. A simple and accurate mathematical model for predicting productivity of multifractured horizontal wells［R］. SPE 114452, 2008.

［3］WEI Y, ECONOMIDES M J. Thrasverse hydraulic fracture from a horizontal well［R］. SPE 94671, 2005.

［4］YUAN Hong, ZHOU Desheng. A new model for predicting inflow performance of fractured horizontal wells［R］. SPE 133610, 2010.

［5］WAN J, AZIZ K. Semi-analytical well model of horizontal wells withmultiple hydraulics fractures［J］. SPE J, 2002, 7（4） : 437-445.

［6］KAMKOM R. Modeling performance of horizontal, undulating and multilateral wells［D］. PhD dissertation, Texas A&M University, College Station, Texas, 2007.

［7］KAMKOM R, ZHU D, BOND A. Predicting undulatingwell performance［J］. SPE Prodction & Operations. 2009, 24（1） : 194- 207.

［8］程林松，李春兰，郎兆新.分支水平井产能的研究［J］.石油学报， 1995， 16（2）：19-55.

［9］SALAS J R, CLIFFORD P J, JENKINS D P. Multilateral well performance prediction［R］. SPE 35711, 1996.

［10］WOLFSTEINER C, DURLOFSKY L J, AZIZ K. Approximate model for productivity of nonconventional wells in heterogeneous reservoirs［J］. SPE J, 2000, 5（2） : 218-226.

［11］王晓冬，于国栋，李治平.复杂分支水平井产能公式［J］.石油勘探与开发，2006，33（6）：729-733.

［12］GUO Boyun, ZHOU Jinkui, LING Kegang. A rigorous composite- inflow-performance relationship model for multilateral wells［J］. SPE J, 2007, 23（2） :241-248.

［13］程林松，兰俊成.考虑水平井筒压力损失的数值模拟方法［J］.石油学报，2002，23（1）：67-71.

［14］OUYANG Liangbiao, AZIZ Khalid. A simplified approach to couple wellbore flow and reservoir inflow for arbitrary well configurations［R］. SPE 48936, 1998.

［15］AZIZ Khalid. A general single-phase wellbore/ reservoir coupling model for multilateral wells［R］. SPE 72467, 2001.

［16］CHEN W, ZHU D, HILL A D. A comprehensive model of multilateral well deliverability［R］. SPE 64751, 2000.

［17］SHI Hua, HOLMES J A, DURLOFSKY L J. Drift-flux modeling of two-phase flow in wellbores［J］.SPE J, 2005, 10（1） : 24-33.

［18］SHI Hua, HOLMES J A, DURLOFSKY L J. Drift-flux parameters for three-phase steady-state flow in wellbore ［J］.SPE J, 2005, 10（2） : 130-137.

［19］KROGSTAD S, DURLOFSKY L J. Multiscale mixedfinite-element modeling of coupled wellbore/near-well flow［J］. SPE J, 2009,14（1） : 78-87.

［20］VICENTE R, ERTEKIN T. Modeling of coupled reservoir and multifractured horizontal well flow dynamics［R］. SPE 101929, 2006.

［21］王明，朱维耀，宋考平.非牛顿流体多分支水平井产能模型及数值模拟［J］.大庆石油学院学报，2006，30（5）：38-41.

［22］HU B, SAGEN J, CHUPIN G , et al. Integrated wellbore/ reservoir dynamic simulation［R］. SPE 109162, 2007.

［23］SHIEDEL Mahdy, SEPEHRNOORI Kamy. Development of a coupled compositional wellbore/reservoir simulator for modeling pressure and temperature distribution in horizontal wells［R］. SPE 124806, 2009.

［24］ZEBOUDJ F, BAHI L. Horizontal well performance flow simulation CFD-application［R］. SPE 133269, 2010.

［25］YUAN Kun, BELLO Oladele. Use of computational fluid dynamics model for evaluating performance of highpressure, high-temperature wells［R］. SPE 167896, 2014.

［26］LIVESCU S, DURLOFSKY L J, AZIZ K. A fullycoupled thermal multiphase wellbore flow model for use in reservoir simulation［J］. Journal of Petroleum Science and Engineering, 2010,71（3-4） :138-146.

［27］THANYAMANTA W, JOHANSEN T E, HAWBOLDT K. Well modeling incorporating nonisothermal effects and asphaltene precipitation［R］. SPE 105129, 2007.

［28］TRINA S, JOHANSEN T. An integrated horizontal and vertical flow simulation with application to wax precipitation［R］. SPE 156555, 2012.

［29］LUO H S, WANG X H, QUINTARD M. Adaptive mesh refinement for one-dimensional three-phase flows in heterogeneous fractured porous media［J］. Numerical Heat Transfer, Part B: Fundamentals, 2008, 54（6） : 476-498.

［30］罗海山，王晓宏，施安峰.裂缝孔隙油藏蒸汽辅助重力泄油过程的自适应网格数值计算［J］.中国石油大学学报：自然科学版，2011，35（1）：140-144.

［31］EDWARDS D A, GUNASEKERA D, MORRIS J, et al .新一代油藏模拟技术［J］.油田新技术，2011，23（4）：4-15.

［32］HOLMES J A, BARKVE T, LUND O. Application of a multisegment well model to simulate flow in advanced wells［R］. SPE 50646, 1998.

［33］STONE T W, BENNETT J, LAW D H S, et al. Thermal simulation with multisegment wells［R］. SPE 78131, 2001.

［34］SEMENOVA A, LIVESCU S, DURLOFSKY L J, et al. Modeling of multisegmented thermal wells in reservoir simulation［R］. SPE 130371, 2010.

［35］HOLMES J A, BYER T, EDWARDS D A, et al. A unified wellbore model for reservoir simulation［R］. SPE 134928, 2010.

［36］EDWARDS D A, CHENG N, DOMBROWSKY T P, etal. Representing hydraulic fractures using a multilateral multisegment well in simulation models［R］. SPE 163644, 2013.

［37］NEYLON K, REISO E, HOLMES J A, et al. Modeling well inflow control with flow in both annulus and tubing ［R］. SPE 118909, 2009.

［38］YOUNGS B, NEYLON K, HOLMES J A. Recent advances in modeling well inflow control devices in reservoir simulation［R］. IPTC 13925, 2009.

［39］ZAREA Marwan, ZHU Ding. An integerated performance model for multilateral wells equipped with inflow control valves［R］. SPE 142373, 2011.

［40］赵国忠，孙巍，何鑫.基于分层注水数学模型的油藏数值模拟［J］.东北石油大学学报，2012，36（6）：82-87.

［41］SAGEN Jan, HU Bin, LIEN Siv Kari, et al. A dynamic model for simulation of integrated reservoir, well and pipeline system［R］. SPE 147053, 2011.

［42］KARIMI-FARD M, DURLOFSKY L J. An expanded well model for accurate simulation of well-reservoir interactions［R］. SPE 141675, 2011.

［43］DING D Y. Coupled simulation of near-wellbore and reservoir models［J］. Journal of Petroleum Science and Engineering, 2011,76（1-2） :21-36.

［44］KARIMI-FARD M, DURLOFSKY L J. Accurate resolution of near-well effects in upscaled models using flow-based unstructured local grid refinement［R］. SPE 141675, 2011.

［45］NAKASHIMA Y, LI H, DURLOFSKY L J. Near-well upscaling for three-phase flows［J］. Computational Geosciences, 2012,16（1） :55-73.

［46］ROJAS Danny, LI Hangyu, KUMAR, Mridul, et al. Development and application of near-well multiphase flow upscaling for forecasting of heavy oil primary production［R］. SPE 165381, 2013.

（修改稿收到日期2015-04-17）

〔编辑朱伟〕

Current status and development tread of coupled wellbore and reservoir numerical simulation technique

GAO Dapeng1,2, WANG Dong3, HU Yongle1
（1. Research Institute of Petroleum Exploration and Development, CNPC, Beijing 100083, China;
2. School of Earth and Space Science, Beijing University, Beijing 100871, China;
3. Research Institute of Oil Production Technology, Shengli Oilfield Company, SINOPEC, Dongying 257000, China）

In this paper, the research progress of coupled wellbore and reservoir numerical simulation technique were summarized from four aspects: well flow equations, wellbore thermal multiphase flow calculation, multi-interval well model, extended well model infilled near wellblock. The paper pointed some main problems: large errors in the parameters of well flow equations, so the accurate source sink term cannot be provided; the multiphase wellbore pipe flow at high watercut stage is very complex, so there are great errors in the commonly used computational fluid mechanics model; the fluid- structure coupling mechanism in non-isothermal well flow is not clearly understood and the numerical calculation takes too long time; simulation of comingled production does not take into account the vertical heterogeneity, and the production of thin reservoirs is not in conformity with reality. The paper presents the concept that the multi-interval model and reservoir coupled numerical simulation technique based on multiphase pipe flow calculation, extended well model and reservoir coupled numerical simulation technique and coupled fluid- structure coupled numerical simulation technique based on sand production and wax scale in the wellbore are the future development tread.

reservoir numerical simulation; multiphase pipe flow calculation; multi-interval well model; extended well model; fluid-structure coupling

TE319

A

1000 – 7393（ 2015 ） 03 – 0053 – 08

10.13639/j.odpt.2015.03.013

国家科技重大专项“高含水油田提高采收率新技术——剩余油分布综合预测与精细注采结构调整技术”（编号：2011ZX05010-002）和“CO2驱油与埋存潜力评价与战略规划”（编号：2011ZX05016-006）。

高大鹏，1989年生。北京大学在读博士生，现主要从事油藏工程及数值模拟研究。E-mail：gaodapeng2015@petrochina.com.cn。

引用格式：高大鹏，王东，胡永乐.井筒与油藏耦合数值模拟技术现状与发展趋势［J］.石油钻采工艺，2015，37（3）： 53-60.