数字体图像中的插值应用与比较
罗方燕,黄旺华(广东职业技术学院信息工程系,佛山 528041)
数字体图像中的插值应用与比较
罗方燕,黄旺华
(广东职业技术学院信息工程系,佛山528041)
0 引言
随着X光三维设备的发展,数据体图像在医学、立体交互、流体力学和原子结构分析中得到了广泛的应用,三维数据体的仿射变换是处理中的基础过程,例如旋转、平移和尺度变换等,在变换过程中需要进程灰度内插[1]。
本文中,首先通过对二维图像处理中常用的插值算进行分析,例如最近邻插值、双线性插值和三次内插法,根据插值的原理,提出依次沿三个坐标轴进行运算的思路,将这三种常用的算法扩展到三维数据体的情形下,三次内插法仍然是三维数据插值中推荐的算法之一。
本文组织如下:首先在第二部分详细介绍了常用的灰度插值法,在第三部分,根据二维插值法的处理原则,将三种常用的插值法扩展到三维数字体图像的灰度插值处理中,在第四部分通过实验验证插值效果,最后在第五部分中,对数学体图像插值进行总结。
1 二维图像插值法分析
在图像处理中,当对图像进行比例缩放、旋转和复合变换等操作时,原始图像的整数像素坐标,经过变换后,绝大多数情况下,在目标图像中所处的位置并非整数,所以对图像进行几何变换时,除了需要进行几何变换,还需要进行图像的灰度级插值处理。
在图像中,只有整数的像素才具有灰度值,为了求取目标图像中的每一个像素的灰度值,如图1所示,一般的做法是对目标图像中的每个像素(x',y')进行逆变换,求取其在原始图像中的像素位置(x0,y0)(一般为浮点数),通过灰度插值法,根据浮点像素(x0,y0)周围整数像素的灰度值,求取灰度值f(x0,y0),并将该位置的灰度值赋值给目标图像中的对应用整数像素(x',y')。在图像处理中,常用的灰度级插值算法有:最近邻插值法、双线性插值法和双三次内插法[2]。
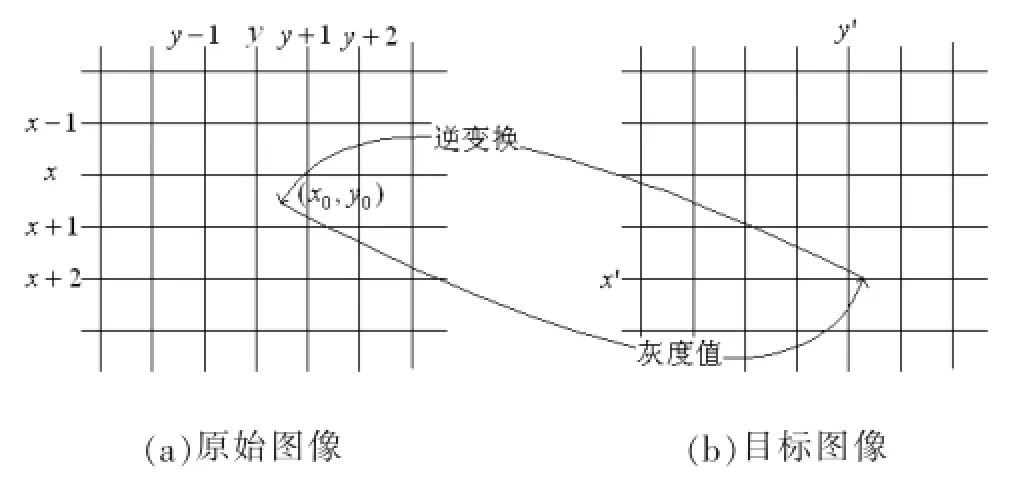
图1 逆变换求灰度值
1.1最近邻插值法
最近邻插值法,也称为零阶插值,是所有插值法中最简单、计算量最小的算法,但效果最差,会留下明显的锯齿痕迹。该算法主要插值原理是以距该浮点像素(x0,y0)最近的整数像素的灰度值赋值给(x0,y0),如图2,如果x0-x<0.5,y0-y<0.5,点(x0,y0)与点(x,y)最靠近,则f(x0,y0)=f(x,y),而在目标图像中g(x',y')=f(x,y)。

图2 最邻近插值原理
1.2双线性插值法
双线性插值法,也称为一阶插值法,是最邻近插值法的改进,该插值算法根据周边4个像素的灰度值,通过两次线性插值计算出f(x0,y0)。如图3,首先根据公式(1)计算f(x,y0)和f(x+1,y0)。然后根据公式(2)计算f(x0,y0):
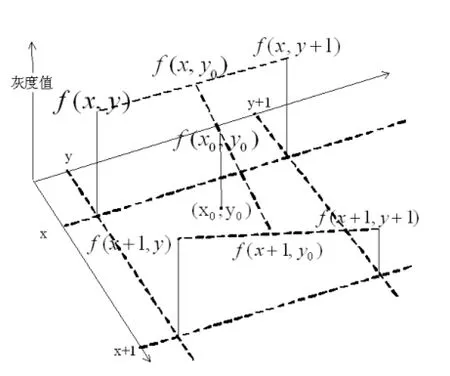
图3 双线性插值


与最近邻插值法相比,双线性插值法考虑了点(x0,y0)周边的4个整像素点的灰度值,其插值效果具有比较大的改观,但仍然会使图像细节丢失而变得轮廓模糊。
1.3双三次内插法
双三次内插法[3],也称为双立方插值法和立方卷积插值法,主要根据与该点最邻近的16个整像素灰度值,并结合像素距离的三次多项式值进行内插,计算浮点像素的灰度值为:

与上述插值法相比,双三次内插法是效果最好,最常用的插值法之一,唯一的缺点是运算量比较大。
2 常用插值法的扩展
通过对二维图像插值法的分析,我们发现三种经典的插值法,都是通过先处理X轴(或Y轴),再处理Y轴(或X轴)的思路,求取浮点像素的灰度值。我们参照此思路,并推广到三维的情况,首先处理Z轴方向,然后再求取X轴和Y轴,将以上三种插值方法扩展到三维数字体图像处理中。
2.1最近邻插值法
在求取浮点体素(x0,y0,z0)的灰度值之前,首先计算浮点部分大小和整数部分体素如果u<0.5,v<0.5,且z<0.5,则f(x0,y0,z0)=f(x,y,z),以此类推,将与浮点体素最近的整数体素的灰度值赋予该浮点体素。
2.2三线性插值法
根据双线性插值的原理,三线性插值将考虑浮点体素周围16个整数体素的灰度整,依次在各个方向上进行一阶插值,首先在Z轴方向,根据2.1计算f(x,y,
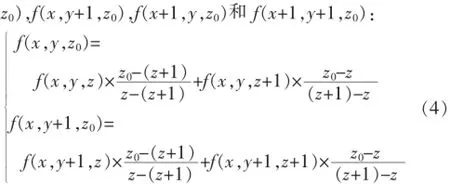
然后在Y轴方向,根据2.2计算f(x,y0,z0)和f(x+ 1,y,z0):

最后在X轴方向计算f(x0,y0,z0):
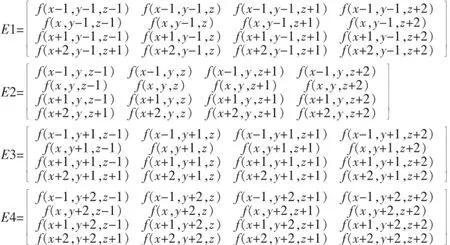

2.3三元三次内插法
三元三次内插法依照各轴分别对待的思路,根据公式(3),扩展到三维情形下,首先通过公式(7)计算出Z轴为浮点的平面:

E1-E4如下。
将同样采用s(x)三次方程进行插值,首先求取Z轴方向,然后直接套用公式(3)。首先计算D=
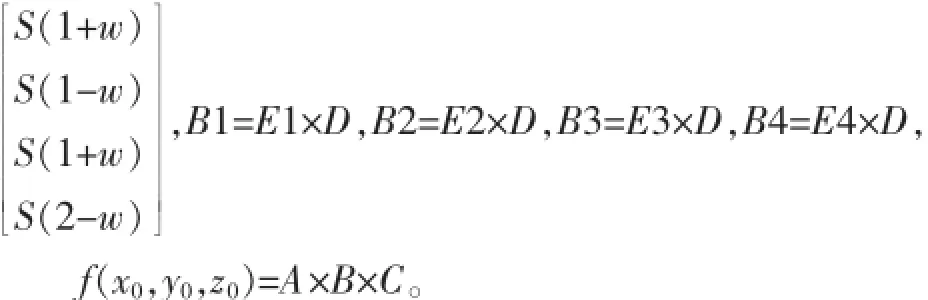
3 实验结果和分析
为了验证三种经典的插值算法在三维数据中的插值效果,在实验中,构造一个81×81×81的三维数体图像,数字体图像中,选定21×21×41的长方体,并设定该长方体的灰度值均为200(其余体素灰度值为0),如图4所示。首先对原始三维数据进行旋转变换 (如图5,6,7的左图),然后进行逆变换(如图5,6,7的右图),在变换和逆变换过程中分别同时应用最邻近插值、三线性插值和三元三次内插法,得到新的三维数据图像,如图5,6,7。
为了客观地评价三种插值算法的效果,在本文中使用峰值信噪比(PSNR)[4],衡量值法的前后两幅数字体图像的差异,计算新数字体图像与原数字体图像之间的PSNR如表1。
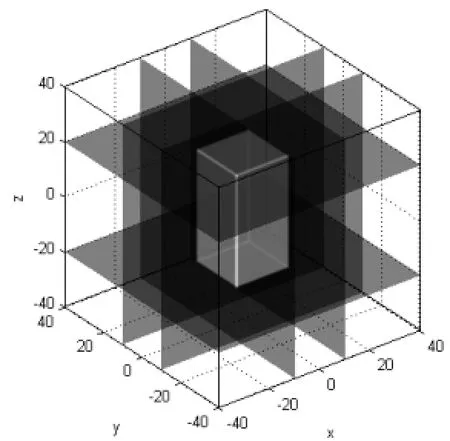
图4 原始数字体图像
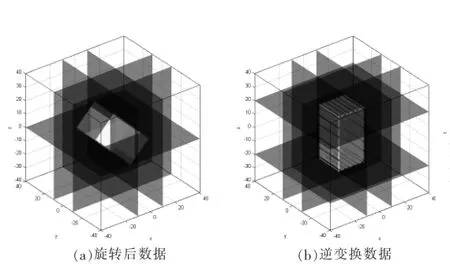
图5 三维最邻近插值

图6 三维三线性插值
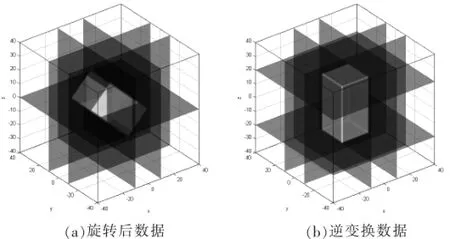
图7 三维三元三次内插
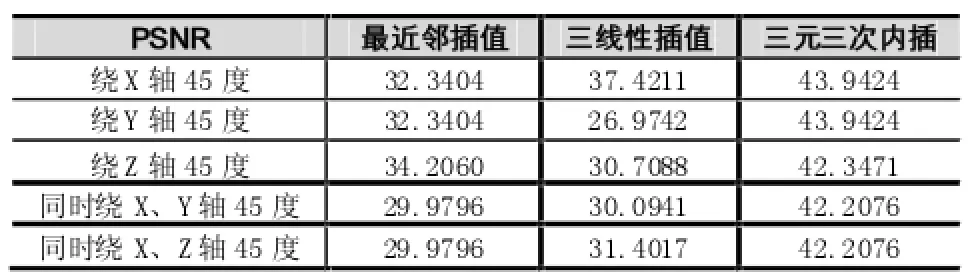
表1 峰值信噪比(PSNR)
从表中,可以发现,在二维插值效果比较好的三次内插法,同样适用于三维插值的情况,同时在客观评价上也高出比较多。而线性插值法,并没有与二维插值情况一致,采用三线性插值,有可能会出现比最近邻插值的PSNR还低,其原因可能是,在线性插值中,使图像细节丢失而变得比较模糊。
4 结语
本文将二维图像插值中常用的方法推广到三维数字体图像中,通过实验表明,三元三次内插法的效果最好,在以后的数字体图像的仿射变换中推荐采用该插值法。插值法在二维图像处理中是比较成熟的技术,除了文中所提到的算法外,还有许多插值算法,例如基于边缘的自适应法[5-6],可以扩展到三维处理的过程中,在以后的研究中将继续关注该方面。
[1]朱瑾,张龙赛,王建华,图像三维插值算法研究.华东船舶工业学院学报,2005,19(5):65-67.
[2]Lehmann,T.M.,C.Gonner,K.Spitzer,Survey:interpolation methods in medical image processing.Medical Imaging,IEEE Transactions on,1999,18(11):1049-1075.
[3]KEY,R.G.,Cubic convolution interpolation for digital image processing.IEEE Transactions on Acoustics,Speech,and Signal Processing,1981,29(6):p.1153-1160.
[4]刘洪臣,冯勇,杨旭强,基于双三次B样条曲面亚像元图像插值方法.哈尔滨工业大学学报,2007.39(7):p.1121-1125.
[5]Battiato,S.,G.Gallo,F.Stanco.A locally adaptive zooming algorithm for digital images.Image and Vision Computing,2002,20(11):805-812.
[6]Chena,M.-J.,C.-H.Huang,W.-L.Lee.A fast edge-oriented algorithm for image interpolation.Image and Vision Computing,2005,23(9):791-798.
DVI Interpolation;Three Linear Interpolation;Ternary Cubic Interpolation
Application and Comparison of Classical Interpolation Method in Digital Volume Image Processing
LUO Fang-yan,HUANG Wang-hua
(Department of Information Engineering,Guangdong Polytechnic,Foshan 528041)
1007-1423(2015)23-0046-05
10.3969/j.issn.1007-1423.2015.23.011
罗方燕(1981-),女,广东梅州人,本科,实验师,研究方向为计算机应用技术
2015-06-17
2015-08-05
三维数字体图像的仿射变换是体数据处理过程中的基本过程,其中插值是仿射变换的重要步骤之一。根据二维图像插值原理,将常用的插值法推广到三维数字体图像中。通过实验表明,三元三次内插法的插值效果最好,而三线性插值法,由于细节模糊,其峰值信噪比略低于最近邻插值法。
数字体插值;三线性插值法;三元三次内插法
黄旺华(1981-),男,广东梅州人,硕士研究生,讲师,研究方向为计算机应用技术
The interpolation is one of the important steps during affine transformation,which is the basic process in digital volume image(DVI)processing.Classical interpolation method is extended to DVI processing based on their principles.Experiments show that the ternary cubic interpolation is the best,and the PSNR of three linear interpolation method is lower than the nearest neighbor interpolation method as blurring of detail.

