随机搜索算法在护理实习生排班问题中的研究与应用
张立,忻凌,王丽,马忻(.安徽中医药大学第一附属医院,安徽 3003;.安徽财贸职业学院,安徽 3007)
随机搜索算法在护理实习生排班问题中的研究与应用
张立1,忻凌1,王丽2,马忻1
(1.安徽中医药大学第一附属医院,安徽230031;2.安徽财贸职业学院,安徽230071)
0 引言
护理实习生排班问题是一种典型的组合优化问题,其目的是对护理实习生的实习期进行合理的安排[1]。该问题的解决一方面需要满足实习生的要求,安排他们进入需要学习的科室,实现实习目标;另一方面需要满足实习科室的要求,使各科室的实习生数量在周期内相对均衡。高质量的排班方案不仅能够满足护理实习生的实习需求,还能够保证医院各科室正常运作。
护理实习生排班问题是一种关于人员日程自动编排的问题[2]。单个实习生的排班问题相对比较简单,但面对实习生数量相对庞大,而实习科室的承受能力极其有限的实际情况,实习生排班问题的求解就变得非常困难。对于护理实习排班问题的研究目前在国内并不广泛,主要集中在排班方法对于教学效果的影响[3-4]上。
传统的人员日程编排问题是将人员的时间顺序看作一条路径,利用不用长度的日程进行填充,使路径中的空闲时长最短。目前,国内研究者对人员日程编排问题进行了广泛的研究:文献[5-7]提出了带约束的护士排班模型,并使用一系列变换规则来求解护士排班问题;王超等[8]对变领域搜索算法进行改进,来解决排班问题。此外,一些研究者从管理角度对人员排班工作进行优化,陆蕊君等[9-10]通过调整班次,重新制定和完善岗位职责,改进排班模式,实行弹性工作制,在一定程度上解决了人力资源与病人期望不平衡的矛盾及护士编制不足、护士班次变换频繁的问题。
护理实习生的排班工作目前仍主要由人工方式完成,工作量很大,而且容易出错,各科室不同时间人员分布也极不均衡。搜索算法利用计算机的高性能穷举一个问题部分的或所有的可能情况,从而求解出问题的解。随机搜索算法实际上是根据初始条件和扩展规则构建一个解答树,解答树上的各解结点随机获得,最终获得一个日程编排问题的解。随机搜索算法能够有效提高工作效率,避免人工方式产生的错误,并通过随机过程在大数据的环境下平衡科室人数。
本文提出一个求解护理实习排班的随机搜索算法,利用随机算法在海量数据分配中的优势,解决排班方案不均衡的问题。
1 护理实习生排班模型
1.1模型约束条件
护理实习排班问题是指为不同院校的学生在给定的实习时间段内安排实习科室,并使该排班方案满足各种硬性约束条件,同时尽量满足各种软性约束条件。硬性约束条件是指在整个排班方案中必须要满足的条件,任何违反硬性约束条件的排班方案都是不可行的;软性约束条件是在排班方案中希望能够得到最大满足的约束。主要的约束条件如下:
(1)硬性约束条件:
①学生的每个周次有必须有安排;
②必去科室必须在实习期内出现;
③回避科室在实习期内不能出现;
④学生进入非单周实习科室实习,必须在指定时间;
⑤同类型科室只能去一个;
⑥各科室的人员安排不得超过其最大承受人数;
(2)软性约束条件:
①实习科室的安排每周人数尽量平稳;
②优先科室尽量靠前安排;
③某大类科室(如内科科室或外科科室)可规定数量选取(最少去1个,最多去N个);
④科室安排尽量齐整,避免出现断档。
上述约束条件是测试数据集中可能出现的约束。对于某一特定院校的数据集来说,并不一定全部出现。因此,这些约束条件能够较好地反映实际应用的不同要求。
1.2护理实习生排版模型
在本文中,我们将单个实习生的排班模型描述为:从某一个时间点开始 (实习生实习期的开始时间),按照一定规则随机选取科室对时间序列进行填充。其中,各实习科室有一下特点:①科室分为1周科室、2周科室和3周科室,实习生在其中的实习时间分别为1周、2周和3周,为了便于管理,2周科室和3周科室分别必须在指定的统一时间安排进入;②同类科室需要回避,同一实习生不能重复去2个同类型科室,例如手术室与介入手术室属于同类科室,脑病1科与脑病2科属于同类科室;③各科室还可分为大类科室,如心内科、内分泌科、消化内科等属于内科科室,普外科、骨科、脑外科等属于外科科室。
下面我们给出一些重要的决策变量和参数:
我们考虑科室的集合D、实习生的集合S和科室负担的集合B。其中科室Di定义为Di(IDi,ki,class1i,class2i,Ni),其中IDi代表科室唯一ID,表示科室属于几周科室,class1i表示科室小类,用于区分同类型科室,class2i表示科室大类,用于区分大类科室,Ni表示科室Di最多可以同时容纳的人数;实习生Si定义为Si(starti,endi,ti),其中starti和endi分别表示实习生实习的起止时间,ti表示实习生当前的时间戳;科室负担Bij定义为Bij(IDi,tj,mij),其中IDi代表科室唯一ID,tj表示科室当前的时间戳,mij表示科室i在时间tj的实际人数,mij必须满足约束条件mij≤Ni,即科室的实际安排人数不得超过最大人数上限。
2 随机搜索算法与流程
随机搜索算法是指每次从科室的集合中随机搜索一个合适的科室填入实习生的时间序列中,直到所有时间填满为止。下面详细描述我们给出的随机算法:
(1)从实习生集合中获取一个学生Si(starti,endi,ti),初始ti=starti。针对实习生的实习要求,将科室集合D划分成必去科室子集D1、回避科室子集D2和其他科室子集D3;
(2)从科室集合中按要求随机搜索一个科室,并验证其是否合适。如果合适,则填入实习序列,具体约束如下:
①如果ti%6=0时,首先从必去科室子集D1中以ki∈{2,3}为条件进行随机抽取;如果所有科室都无法满足硬性约束的要求,则从其它科室子集D3中以为条件进行随机抽取;如果所有科室都无法满足硬性约束的要求,则从必去科室子集D1中以ki=1为条件进行随机抽取;如果所有科室都无法满足硬性约束的要求,则从其它科室子集D3中以ki=1为条件进行随机抽取;如果仍然无法满足,则当前时间戳ti=ti+1,空闲时间Ti=Ti+1;
②如果ti%3=0时,首先从必去科室子集D1中以ki=3为条件进行随机抽取;如果所有科室都无法满足硬性约束的要求,则从其它科室子集D3中以ki=3为条件进行随机抽取;如果所有科室都无法满足硬性约束的要求,则从必去科室子集D1中以ki=1为条件进行随机抽取;如果所有科室都无法满足硬性约束的要求,则从其它科室子集D3中以ki=1为条件进行随机抽取;如果仍然无法满足,则当前时间戳ti=ti+1,空闲时间Ti=Ti+1;
③如果ti%2=0时,首先从必去科室子集D1中以ki=2为条件进行随机抽取;如果所有科室都无法满足硬性约束的要求,则从其他科室子集D3中以ki=2为条件进行随机抽取;如果所有科室都无法满足硬性约束的要求,则从必去科室子集D1中以ki=1为条件进行随机抽取;如果所有科室都无法满足硬性约束的要求,则从其它科室子集D3中以ki=1为条件进行随机抽取;如果仍然无法满足,则当前时间戳ti=ti+1,空闲时间Ti=Ti+1;
如果ti%3!=0且ti%2!=0时,首先从必去科室子集D1中以ki=1为条件进行随机抽取;如果所有科室都无法满足硬性约束的要求,则从其它科室子集D3中以ki=1为条件进行随机抽取;如果仍然无法满足,则当前时间戳ti=ti+1,空闲时间Ti=Ti+1;
⑤插入3周科室时,必须遵循条件endi-ti+1>=3;插入2周科室时,必须遵循条件endi-ti+1>=2;插入1周科室时,必须遵循条件endi-ti+1>=1。
(3)安排科室成功后,则重复步骤(2),继续安排科室,如果ti>endi,则排班成功,退出循环。
3 实验结果与分析
针对护理实习生排班问题,本文提出了一个随机搜索算法。该算法不仅能够实现护理实习生排班的自动化,而且能够解决科室人数分布不均衡的问题。下一步将对该算法进行实现,并使用数据对进行检验。
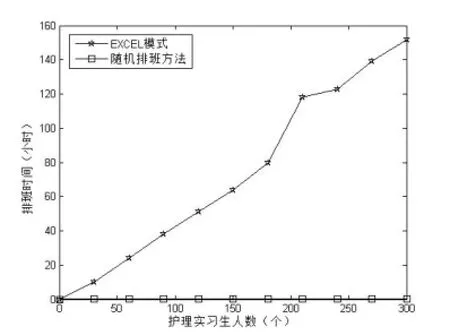
图1 排班时间对比图
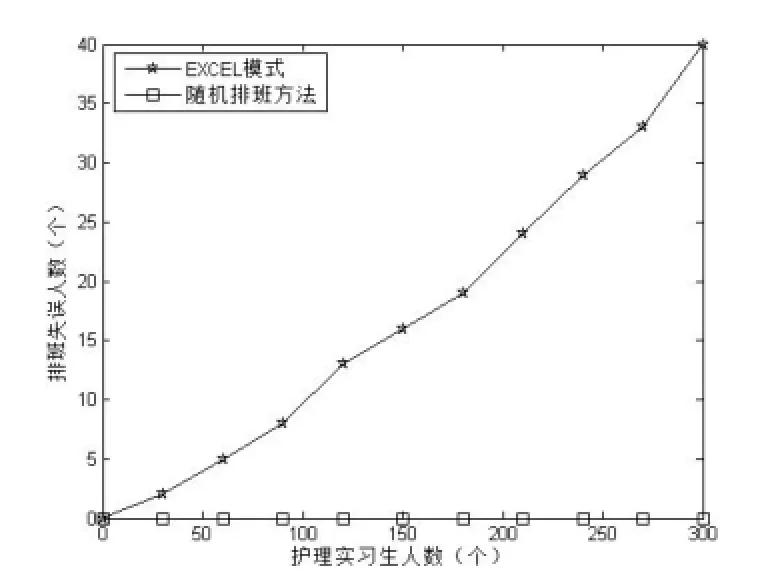
图2 排班正确率对比图
(1)排班效率
本文在人工模式排班累计统计了300名护理实习生所消耗的时间,并对比了本文实现同样人数的排班所消耗的时间,对比结果如图1所示。
由图1,发现传统的排班方式在处理这么大人数的排班消耗的时间远远大于本文实现方法,本文的实现方法只需要数分钟就能一次完成数百名护理实习生的排班。因此,本文的实现方法大大地提高了护理实习生排班的效率。
(2)排班正确率
本文搜集了利用传统的方式排班300名护理实习生的失误人数,并对比了本文的实现方法,如图2所示。
由图2可知,本文的实现方法的正确率远远高于传统的排班方式。同样,证明了本文的实现方法的稳定性。
(3)排班均衡问题
关于排班均衡的问题,并没有一个严格的标准来衡量,但从本文方法实施之后的反馈来说,科室的护理实习生基本上达到均衡,护理实习生实习的科室也比以前丰富,而且实习的效果也比以前好。这侧面反映了本文实现方法基本上解决了排班不均衡的问题。
4 结语
本文根据护理实习的约束条件提出了护理实习生的排班模型,并将随机搜索算法应用到护理实习生的排班中,实验结果表明本文的护理实习生的排班相比较于传统的排班模式,在排班效率、排班的准确率上都有很明显的提升,并解决了排班的均衡问题。但本文的方案是针对于护理实习生的排班,对于其他护士的排班是否有同样的效果并没有验证,因此,本文的下一步研究方向是提出针对所有护理人员的排班实现与改进。
[1]谢屹红.护士排班方式与护理人力资源的合理利用[J].中国实用护理杂志,2004,20(4):65-65.
[2]BRUCKER P,QU R,BURKE E.Personnel scheduling:models and complexity[J].European Journal of Operational Research,2011.467-473.
[3]黎建敏,林婉萍.APN排班工作职责作为实习目标的临床护理教学效果初探[J].国际医药卫生导报,2011,17(1):120-122.
[4]史爱玲等.一对一带教与排班制带教在护理实习生中的教学效果比较[J].齐鲁护理杂志,2014,(8):12-13.
[5]沈吟东,陈名晖,邓婕.利用矩阵向量化变换求解护士排班问题[C].中国控制与决策会议论文集,2008:1019-1022.
[6]柯彩霞,谢文,刘晓华,等.护士排班模式改革与效果[J].中国护理管理,2008,8(11):38-40.
[7]冯艮娇,卢海涛.护理排班模式改革探讨[J].南方护理学报,2002,9(4):67-68.
[8]王超,董兴业.求解护士排班问题的变领域搜索算法[J].计算机应用,2013,33(2):338-341,352.
[9]陆蕊君,鲍学英,王惠芬.护士排班方法的改进与实践[J].当代护士:综合版,2007(2):23-23.
[10]唐富琴,张琳.人性化管理在护士排班中的运用[J].护理学报,2009,16(16):18-19.
张立,男,安徽合肥人,初级工程师,研究方向为计算机技术
忻凌,男,安徽合肥人,工程师,研究方向为人工智能
马忻,女,安徽合肥人,副教授,研究方向为护理学及其管理
王丽,女,安徽合肥人,讲师,研究方向为信息管理
Nursing Practice;Random Algorithm;Scheduling
Research and Application of Stochastic Search Algorithm in the Scheduling Problem of Nursing Interns
ZHANG Li1,XIN Ling1,WANG Li2,MA Xin1
(1.The First Afflicted Hospital of Anhui University of TCM,Anhui 230031;2.Anhui Finance&Trade Vocational College,Anhui 230071)
1007-1423(2015)23-0035-04
10.3969/j.issn.1007-1423.2015.23.008
2015-05-12
2015-08-05
临床护理教学是各教学医院的一项重要工作。目前,各医院多采用人工方式完成护理实习生排班工作,但由于实习生数量较大、进岗时间不一、实习大纲要求复杂等原因,使实习生排班工作出现工作量大、易出错、科室分配不均衡等问题。提出将随机搜索算法应用在护理实习生排班中,并从排班效率、排班正确率以及排班均衡问题上对比传统的排班方式。实验结果表明:将随机搜索算法应用于护理实习生排班中,发现排班效率、排班准确率高,而且可避免排班不均衡的问题。
护理实习;随机算法;排班
安徽中医药大学临床科研基金(No.2012LC1-026B)
The clinical nursing teaching is an important task in the teaching hospitals.At present,most hospitals manually finish scheduling work of nursing interns,but with large quantities of interns,different time of punching in the post,complex requirements of guideline for internship and other reasons,there are many problems existed in the scheduling work,such as heavy workload,error-prone problems,and the uneven distribution of the department.Presents the random search algorithm applied in nursing interns scheduling,and makes comparison with traditional scheduling methods in view of the efficiency,accuracy and equilibrium of scheduling.The experimental results show that,when the random search algorithms is applied to the nursing trainee scheduling,efficiency and accuracy rate are higher,and the problem of unbalanced scheduling are avoided as well.

