基于微正则退火算法对K-means 聚类算法的优化
周浩理,李太君,肖 沙
(海南大学 信息科学技术学院,海南 海口570228)
K-means 算法是经典的基于划分的聚类算法,虽然已经被提出近60 年,但仍然是聚类分析中研究的热点问题。因为其简单、高效的特点,在许多领域中都有着广泛的应用。对于数据簇比较密集、簇与簇之间有着明显区别的情况下,使用K-means 聚类算法进行聚类的效果良好;在处理大数据的情况下该算法也有着相对可伸缩和高效率的优点。但该算法也有难以解决的问题:依赖于初始聚类中心、容易陷入局部最优解、对孤立点敏感、需事先指定聚类的数目等。针对其对初始聚类中心的依赖和容易陷入局部最优等缺点,学者们提出了多种改进策略以改进K-means 算法,而改进算法主要分为两类。一类是从算法本身着手,改进初始聚类中心的选取,比如,赖玉霞提出了基于密度的K-means 算法,从数据的自然分布来选取初始聚类中心,找出分布密集的区域作为聚类划分,减少了聚类中心随机选取对聚类结果造成的不稳定性[1]。陈光平利用最大距离作为初始聚类中心划分的标准,将相距较远的聚类中心作为K-means 算法的初始聚类中心,得到较好的聚类结果[2]。另一类是结合其他寻优算法,而主要的算法是智能算法,WANG 利用自组织特征映射神经网络选取初始聚类中心,再采用K-means 算法聚类,克服了Kmeans 算法的缺点[3]。黄浩提出将模拟退火算法与K-means算法结合进行聚类分析,前期利用K-means 算法求出聚类划分结果,在后期结合模拟退火算法,检验聚类结果的准确性[4]。本文考虑到微正则退火算法比模拟退火算法更具有高效全局寻优特性,因此,在K-means 聚类算法的基础上结合微正则退火算法进行了改进。
1 K-means 聚类算法
K-means 算法属于无监督学习,样本中设有给定类别标签y,给定训练样本{x(1),x(2),…,x(m)},其中x(i)∈Rn,将样本聚类成k 个簇,具体实现的基本步骤如下:
1)随机选取给定的k 个聚类质心点μ1,μ2,…,μk∈Rn。
2)重复以下过程直到目标函数收敛:
对于每个样例i,计算其属于的类

对于每个类j,重新计算该类的质心

式中:c(i)的值是1 ~k 个类中的一个,其代表k 个类与样例i距离最近的类。质心μj是对属于同一个类的样本中心点的猜测。
2 微正则退火算法
微正则退火算法基于微正则系综的概念,微正则系综与外界之间没有物质和能量的交换。在一定时间内系统的能量守恒,系统处于任意状态的概率是相等的。但实际上对温度的测量结果可以得出温度的大小还是会有相应变化的[5]。微正则退火算法和模拟退火算法的最大不同是不再直接依赖系统的温度,在退火的状态转移中不再使用Metropolis 准则,而是基于一种确定性的方式[6]。其配分函数为
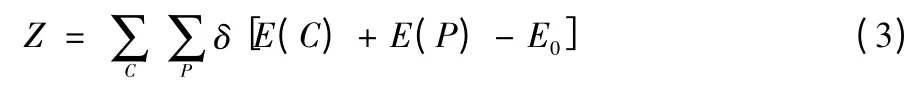
式中:E0为初始能量值;E(C)表示在状态C 时系统的能量,E(P)为在C 状态下动量P 的能量值。
在微正则退火算法的运算过程中,“妖”为一种能量载体,初始化它的动量为P。“妖”可以在状态空间内任意移动,而当“妖”的状态变化时,系统的能量会随之变化,最后系统会摆脱亚稳态。在这个运算中,系统和“妖”的能量和将在一定时间段内为一常量。设ED为“妖”的能量,且其初始值在正常情况下为0,当变化时是一个正数。Z 的形式为
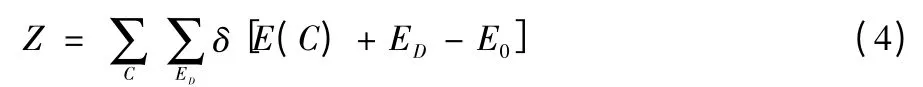
设定系统初始的能量状态后,能量载体“妖”在状态空间中被释放,按上式的初始条件,令“妖”的初始能量值为零,当“妖”移动后,系统能量需要重新进行测定,而当系统能量表现为能量下降时,“妖”接受新状态,且能量值增大,如下所示

式中:Enew,Eold分别表示系统在新旧状态时所对应的能量;为新状态下的能量为旧状态下的能量。因为只有系统的能量表现为下降时,“妖”才接受新状态,因此,经过多次移动后,系统的能量为下降的趋势。
3 微正则退火K-means 算法
3.1 算法原理
K-means 在聚类分析过程中,可能会陷入停滞状态,即算法陷入局部最优。如何跳出局部最优,获得全局最优解是非常关键的问题。李梓提出首先使用模拟退火算法智能搜索初始聚类中心,再利用K-means 算法进行聚类,减少了算法陷入局部最优解的概率[7]。模拟退火算法需要生成随机数并按照Metropolis准则来判断拒绝或接受新状态,但微正则退火实行确定性的状态转移规则,无须生成随机数来判断接受或者拒绝新状态,在大规模问题上要比模拟退火算法更有时间效率[8]。因此,可以采用全局寻优能力更强的微正则退火算法对K-means算法进行优化,摆脱以往算法在寻优方面的局限性。
本文首先对样本进行随机划分,对微正则退火算法进行初始化,然后用微正则退火算法得到聚类的聚类中心,也即全局最优解,然后再把聚类中心交给K-means 算法,再对其进行聚类,得到聚类结果。其算法主要步骤的流程图如图1所示。

图1 微正则退火K-means 算法的主要步骤的流程图
3.2 参数的设定
作为“妖”的能量上界初始值,依据上式能量函数取值范围,应被设定为适中的大小。在选择系统的参数时,设p为下降参数;×p 表示为对能量函数进行几何下降处理。微正则退火算法进行最优解搜索主要变现为:当>为常数时,p 变化;或当p 为常数时, 变化的情形。当p 为常数时,与算法的复杂度成正比;当为常数时,p 不会影响算法对最优解的搜索结果。从以上分析可知,需要明确标定能量上界参数、能量下降参数p,得到2 个参数的最佳组合,以此寻优全局解。
在微正则退火算法中,能量调整因子q 也将影响到算法的搜索成功率。当取q 为过大或过小值时,“妖”的能量会相应出现增大或缩减过度的现象,而对于q 的取值,进行了不同的测试,并得出最为合适的结果[9]。在界定算法进行过程所处的位置时,引入界定参数r,以此为算法进行相应的能量奖励策略;设定t 为进行能量调整策略的参考值,取值空间为[0,1]。
对于K-means 算法的判断准则,本文选取当前聚类划分的总类间离散度作为目标函数

式中:聚类的划分为w,各聚类中心和对应样本之间的距离总和为Jw,样本向量为X,以及第i 个聚类中心为,样本到对应聚类中心的距离为d)。
3.3 算法的具体流程
1)对样本进行随机划分,得到初始状态t1,t2,…,tk,聚类空间S;将S 作为退火的解空间,初始化循环变量i=1,j=1。
2)系统能量E0=0,在状态空间中设定一个行走的“妖”,令其能量初值为ED=0。
3)循环4)~8),直到i >N,即遍历完聚类空间S 中的所有结果。
4)设定“妖”的能量上界Edmax,即Edmax=Edmax×p(p 为能量下降参数)。
5)重复6)、7)、8),直到j >jmax,jmax为循环变量j 的上界,即执行完所有可能变换。
6)在状态空间中,当“妖”产生新解(表现为“妖”进行移动),得到ΔE,即系统相邻状态的差值。
7)当ED>Edmax×t,实行能量缩减ED=ED×(1-P)。如果ED>ΔE,则接受新的系统状态,更新最优状态数组,并检查“妖”的能量是否已越界,即ED是否大于Edmax;否则拒绝新解,当ED<E0×r,实行奖励ED=ED×(1+q)。
8)如果连续若干次拒绝新解,将状态回溯,重新移动。
9)得到全局最优的聚类中心,即为K-means 算法的初始聚类中心,进行聚类,使目标函数收敛,得到聚类结果。
4 实验研究
4.1 数据集的选择
为了测试微正则退火K-means 算法的性能,本文采用UCI 数据库进行测试,UCI 数据库是加州大学欧文分校(University of California Irvine)提出的,目前,该数据库共有187 个数据集,是常用的进行数据挖掘实验的标准测试数据集。UCI 数据可以使用MATLAB 的dlmread 或textread 函数读取,也可以导入,进行测试非常方便,不过需要先将非数字的类别用数字替换,否则不能读入数值。本文的实验环境和算法运行参数配置如下:在Windows 7 系统下,4 核,CPU 处理速度3.20 GHz,4 Gbyte 内存,采用MATLAB 2010b 编写程序。为了能够和其他研究算法进行对比,本文在数据库中选取研究人员常用的测试聚类算法性能的6 个数据集:Iris、Image、Glass、Balance、Wine 和Zoo,通过这6 个数据集来测试Kmeans 算法、模拟退火K-means 算法和微正则退火K-means算法性能的优劣,具体数据集描述见表1。

表1 测试数据集
4.2 实验结果和分析
本文通过直观的二维散点图、查准率和查全率以及运行时间对算法进行比较。为了方便显示,二维散点图采用Iris 数据集的花瓣长和花瓣宽作为横纵坐标,如图2、图3、图4 所示。

图2 基于K-means 算法的仿真结果
图2 可以得到K-means 算法陷入局部最优,图中的3 类数据分类失败,即收敛于局部极值的情况;图3 是基于模拟退火算法的聚类结果,从图中可以看出该算法对数据的分类结果是准确的;图4 是基于微正则退火算法的聚类结果,从图中

图4 基于微正则退火K-means 算法的仿真结果
可以看出该算法对3 类数据的分类准确,而且和图3 的结果图进行对比可知,本文提出的算法达到了模拟退火K-means 算法的分类结果的准确度,2 种算法得到的分类结果比较接近。从图2 和图4 可直观看出微正则退火K-means 算法的聚类效果比K-means 算法更显著,能够摆脱局部极值点的束缚。经过对每个数据集的多次仿真实验,得出表2 的测试结果。
表2 为3 种算法的测试结果的比较,CP 为查准率,即聚类得到的正确结果与得到的全部结果的比值,CR 为查全率,即聚类得到的正确结果与测试数据集中全部的正确结果的比值。RUNTIEN 是CPU 运行时间。从表中数据可以看出,微正则退火K-means 算法的查准率和查全率都要高于经典的K-means 算法和模拟退火K-means 算法,而且通过图2、图3和图4 的二维散点图也可以看出改进的算法和基于模拟退火K-means 算法一样能够优化聚类结果,使之能够摆脱局部最优解的束缚。但是在运行时间上,微正则退火的K-means 算法和模拟退火K-means 算法都要大于K-means 算法,这是由于微正则退火算法和模拟退火K-means 算法在执行过程中寻求全局最优解增加搜索时间,在寻找最优解的过程中,本文改进的算法的运行时间要低于模拟退火K-means 算法,可知,本文改进的算法在运行效率上有明显的提升,从实验仿真结果表明本文算法的改进还是比较成功的,聚类的效果较改进前有明显提升。

表2 3 种算法的测试结果
5 结束语
本文将K-means 算法和微正则退火算法进行有效结合,提出了微正则退火K-means 算法,由于K-means 算法存在需要事先指定聚类的数目、容易陷入局部最优解、对孤立点敏感、依赖于初始聚类中心等缺点,本文利用微正则退火算法针对这些缺点进行了有效的改进,实验表明,改进算法是可行的,对K-means 算法诸多缺点也有很好的鲁棒性,是一种改进K-means 算法性能的可行方案。改进后的算法延长了运行时间,相对于模拟退火K-means 算法的运行效率,本文的运行效率有一定的提高,往后可以在运行效率上进一步研究改进。
[1]赖玉霞,刘建平. K-means 算法的初始聚类中心的优化[J].计算机工程与应用,2008,44(10):147-149.
[2]陈光平,王文鹏,黄俊. 一种改进初始聚类中心选择的K-means算法[J].小型微型计算机系统,2012,33(6):1320-1323.
[3]WANG H B,YANG H L,XU Z J,et al. A clustering algorithm use SOM and K-means in intrusion detection[C]//Proc. International Conference on E-Business and E-Government. Guangzhou:IEEE Press,2010:1281-1284.
[4]黄浩,肖立志,张国毅.基于模拟退火的K-means 算法研究[J].舰船电子对抗,2008,31(6):103-105.
[5]CREUTZ M. Microcanonical Monte Carlo simulation[J]. Physical Review Letters,1983,50(19):1411-1414.
[6]XUE G X,WANG X F,WEI L,et al. An improved microcanonical mean field annealing algorithm[C]//Proc. ICINIS’09. Tianjin:IEEE Press,2009:542-545.
[7]李梓,于海涛,贾美娟.基于改进模拟退火的优化K-means 算法[J].计算机工程与应用,2012,48(24):77-116.
[8]徐俊杰,忻展红. 具有能量奖励策略的微正则退火算法[J].小型微型计算机系统,2008,29(10):1842-1844.
[9]徐畅.大规模路网下基于蚁群微正则退火算法的路径优化方法研究[D].长春:吉林大学,2013.

