基于连通度和加权校正的移动节点定位算法

侯 华，施朝兴

(河北工程大学a.装备制造学院;b.信息与电气工程学院，河北 邯郸056038)

无线传感器网络在家居、救灾、环境、医疗等诸多领域中有着非常广阔的应用前景和巨大的研究价值［1］，研究内容涉及多个方面，包括节点定位算法、路由算法、数据融合、拓扑控制、网络安全等，其中节点定位问题是近年来无线传感器网络中的研究难点和热点［2］。

无线传感器网络定位算法依据在定位时是否依赖节点间距离可以分为测距算法和非测距算法［3］。测距算法需要额外的硬件测量节点间的距离，定位精度相对较高，常见测距算法有接收信号强度指示(RSSI)［4］、信号到达时间(TOA)［5］、信号到达角度(AOA)［6］等;非测距算法利用节点间的连通性估计节点位置，如距离向量－跳段算法、质心算法等，不需要额外添加硬件，定位成本低，但定位精度也相对较低，所以在精度要求不高的应用中具有优势。

跟踪定位等动态网络应用中未知节点一般具有一定的移动特性，上述静态传感器网络定位算法不满足精度要求，需要设计出更有效的移动节点定位算法。Hu Ling－xuan 等人基于蒙特卡罗随机化采样提出了适用于移动节点定位跟踪的MCL 算法［7］，提供了一种很好的研究思路。在此算法的基础上，研究人员对MCL 算法进行了改进。孙燕等人利用曲线拟合求出后验密度分布取值相对较大区域，并改进了样本节点的权值，减少了定位所需的样本数［8］。李伟等人提出一种基于RSSI 的改进蒙特卡罗定位算法，提升了预测的准确率和定位速度，降低了节点能耗［9］。阔永红等人提出利用邻居节点广播信息进行定位的算法，提升了节点的利用效率［10］。本文提出了一种基于连通度和加权校正的移动节点定位算法，定位精度与蒙特卡罗算法相比有明显的提升，并且在一定参数条件下与改进的蒙特卡罗算法具有同等精度。

1 基于连通度和加权校正的移动节点定位算法

1.1 基于连通度的信标选择

无线传感器网络中，固定信标节点周期性地向周围广播自身位置信息和身份信息。未知节点移动过程中，会收到来自多个信标节点的广播，通信范围内的信标也在时刻变化，所以将时间划分为若干时隙，在一个时隙T 内，未知节点监听并记录信标节点的广播信息，时隙结束时利用连通度公式计算各信标节点与未知节点间的连通度，连通度［11］定义为

式中:Ci表示信标Bi与未知节点间连通度;nr表示一个时隙T 内，未知节点接收到来自信标Bi的广播信息数目;ns表示一个时隙T 内，信标Bi发送的位置信息数目。连通度表示一个时隙T 内，各信标节点与未知节点之间的连通性。连通度为0，表示信标Bi与未知节点不连通;连通度为1，表示信标Bi在T 内一直与未知节点连通。

依据连通度值的大小，选取连通性最好的a 个信标节点。这里不采用固定连通度阈值选取信标的方法，而是采用信标个数的选取方法，这是为了保证在连通性不好或信标密度小时也有足够的信标数来进行定位计算。

1.2 自校正测距算法

RSSI 测距算法由于硬件设备简单、通信开销小、成本低、易实现而受到广泛关注，但是它易受外界环境影响，比如会因为反射、多经、非视距等问题产生较大传播损耗，使RSSI 测距精度降低，最终使得定位精度降低。所以如何提高RSSI 精度是一个关键问题。

1.2.1 RSSI 测距模型

文献［12］中，详细介绍了无线电的传播特性。理想状况下，无线电自由空间传播损耗模型为

式中:PL(d)为信号经过距离d 后的路径损耗，单位为dB;d为发射节点到接收节点的直线距离，单位为km;f 为发射频率，单位为MHz;n 为路径损耗因子，范围为2～4。

在实际环境中，常采用对数－常态分布模型，即

式中:P 为发射功率;G 为天线增益;d0=1 m;X 是均值为0、标准差为4～10 的高斯随机变量。

结合式(2)～(4)，即可计算出测量距离d。并且，由此可以得出接收信号强度与距离曲线图，如图1 所示。从图中可以分析出，随着距离的增加，同等大小的RSSI 偏差产生的距离误差也在增大，所以应当尽量选取距未知节点较近的信标参与定位计算。在计算时，较远信标比较近信标包含更大RSSI 误差，为此，引入文献［13－14］中RSSI 自校正的思想，修正测量距离的同时，降低距离较远的信标的作用程度。

1.2.2 距离自校正模型

受实际环境中障碍物等因素影响，RSSI 并不能满足分布模型，需要对RSSI 值修正才能降低定位误差。距未知节点最近的信标节点与它有着相似的环境，可以利用对该信标测距时产生的误差来修正对未知节点进行测距时产生的误差。

图1 RSSI 与距离曲线图

首先，求出各信标的校正系数。当信标节点广播自身信息后，信标节点Bi即可获得通信范围内信标Bj的位置和两点间的RSSI。信标节点的位置是已知的，根据式(5)两点间距离公式可求出它与通信范围内各信标间实际距离。

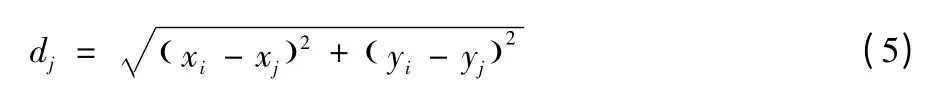
式中:(xi，yi)为信标节点Bi坐标;(xj，yj)为Bi通信范围内信标Bj坐标。

同样可以得到测量距离dij，定义信标节点Bi的加权校正系数λ 为

式中:ρj为加权因子;n 为信标节点Bj的个数;dij为Bi与Bj的测量距离。

在未知节点定位时，得到未知节点与某信标节点间测量距离为d'，距未知节点最近的信标节点的校正系数为λ，则该信标节点与未知节点间校正距离d0为

1.3 定位计算

移动节点在某一位置获得3 个或3 个以上的与其通信的信标节点，利用最小二乘法［15］可估计出未知节点坐标。假设未知节点坐标为(x，y)，通过连通度选择后得到的定位信标m 个，未知节点到第i 个信标(xi，yi)的校正距离为d0i，可得方程组估计为

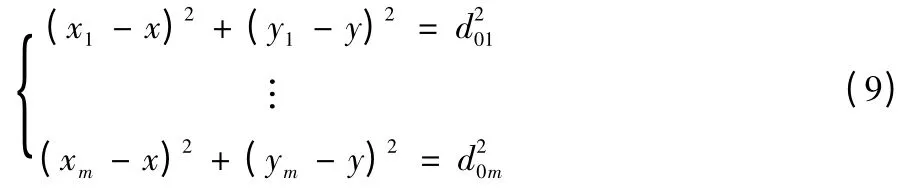
其估计结果为

其中

2 仿真结果与分析

本文在MATLAB 环境下进行仿真，并同MCL 和改进的MCL 算法［16］进行了比较，并且将差分校正和加权校正方法进行了比较。无线传感器区域设置为100 m×100 m，固定信标节点在区域中分布均匀，移动节点以1 m/s 的速度做匀速运动。默认的仿真参数为:信标节点个数为36，通信半径为65 m，衰减因子为2.45，载波频率为2 400 MHz，高斯随机变量X 的标准差为5，天线增益为1 dB。定位过程重复进行100次，仿真结果取平均值。节点位置误差计算采用绝对误差计算公式，即

式中:N 为仿真次数;r 为节点通信半径;(xi，yi)为未知节点的估计位置;(x，y)为未知节点的真实位置。

节点通信半径的大小对定位误差的高低起到比较大的作用。如图2 所示，随着通信半径的增大，4 种定位算法的定位误差都在减小。对于蒙特卡罗算法，这是由于通信半径的增大使得观测信息随之增多，排除了部分无效粒子，但是当r 增大到一定程度后，两种蒙特卡罗算法的误差变化趋于稳定，并且改进的MCL 算法明显好于传统MCL。基于连通度的差分校正和加权校正算法，随着r 的增大，误差先是减小，这是由于r 的增大使得未知节点通信范围内的信标节点逐渐增多，得到了更多的有用位置信息使得定位精度增大。之后，随着r 的增大，误差不再减小，反而有了增大的趋势，这是由于r 的增大包含进了更多离未知节点较远的信标节点。由图1 可知，远距离节点包含了更大的RSSI 误差，此时RSSI 误差增大作用超过了位置信息增加的作用。从图2 中可以看出加权校正优于差分校正，而且在r ＞65 m 后的误差增大趋势小于差分校正，这是因为加权校正降低了远距离信标节点的权重，减小了RSSI 误差增大对定位精度的影响。整体来看，基于连通度和加权校正的移动节点定位算法与改进的蒙特卡罗算法在r 为55～75 m 间有着相近的精度，但是前者的算法计算量小于后者，有更好的应用性。

在信标节点密度对定位误差的影响实验中，依次改变信标节点个数，得到如图3 所示的仿真结果。随着信标节点的增多，未知节点获得了更多的位置信息，4 种定位算法的误差稳定减小，并趋于平缓。而且，基于连通度和加权校正的移动节点定位算法相比传统MCL、基于差分校正的移动节点定位算法有更小的定位误差，能够达到与改进的MCL 算法相近的精度。

图2 通信半径对定位误差的影响

图3 信标个数对定位误差的影响

另外，由上述信标选择、RSSI 测距误差校正和定位计算的过程可以看出:假设n 为传感器节点的平均邻居节点个数，对于基于连通度和加权校正的移动节点定位算法，算法的时间频度是关于n 的一次函数，那么很容易得出该定位算法的算法复杂度为O(n)，计算量小于蒙特卡洛算法，这是因为蒙特卡罗算法的精度依赖于大量的采样样本和多次的迭代计算，使得计算量增加，定位速度变慢。

3 总结

本文提出了一种基于连通度和加权校正的移动节点定位算法。通过保障信标节点与未知节点间的连通性，校正RSSI测距误差，降低远距离信标RSSI 大误差的影响，实现定位精度的提升。仿真实验表明，该算法相比蒙特卡罗算法，相对平均定位误差减小了约10%～30%;随着节点通信半径的增大，定位误差逐渐减小，当r 在60～70 m 范围内，定位误差达到最小;随着信标密度的增加，定位误差也随之减小，当信标密度达到一定数值后，定位误差变化趋势趋于平缓。

［1］张浩，吕真，连卫民，等.采用入侵杂草优化算法的WSN 定位精度提高方法［J］. 电视技术，2014，38(3):146－149.

［2］韩毅刚，王大鹏，李琪，等.物联网概论［M］.北京:机械工业出版社，2012:128－129.

［3］孙利民，李建中，陈渝，等.无线传感器网络［M］.北京:清华大学出版社，2005:142－157.

［4］KALTIOKALLIO O，BOCCA M. Real－time intrusion detection and tracking in indoor environment through distributed RSSI processing［C］//Proc.IEEE 17th International Conference on Embedded and Real－Time Computing Systems and Applications. Toyama:IEEE Press，2011:61－70.

［5］XU Enyang，DING Zhi，DASGUPTA S. Target tracking and mobile sensor navigation in wireless sensor networks［J］.IEEE Trans.Mobile Computing，2013，12(1):177－186.

［6］CHANG D C，FANG Mengwei. Bearing－only maneuvering mobile tracking with nonlinear filtering algorithms in wireless sensor networks［J］.IEEE Systems Journal，2014，8(1):160－170.

［7］HU Lingxuan，EVANS D. Localization for mobile sensor networks［C］//Proc. the 10th Annual International Conference on Mobile Computing and Networking. Philadelphia:IEEE Press，2004:45－57.

［8］孙燕，尚军亮，刘三阳.基于采样优化的蒙特卡罗移动节点定位算法［J］.系统工程与电子技术，2010，32(9):2001－2004.

［9］李伟，丁勇，于春娣，等.一种基于RSSI 的改进蒙特卡罗定位算法［J］.计算机应用与软件，2013，30(12):280－283.

［10］阔永红，周文文，陈健. 避免非视距影响的蒙特卡罗移动节点定位方法［J］.西安电子科技大学学报:自然科学版，2014，41(1):6－12.

［11］朱晓娟，孟祥瑞.基于加权质心的无线传感器网络移动节点定位算法［J］.计算机工程与科学，2011，33(11):15－19.

［12］李建东，郭梯云，邬国扬.移动通信［M］.西安:西安电子科技大学出版社，2006.

［13］王新芳，张冰，冯友兵.基于粒子群优化的改进加权质心定位算法［J］.计算机工程，2012，38(1):90－95.

［14］程秀芝，朱达荣，张申，等. 基于RSSI 差分校正的最小二乘－拟牛顿定位算法［J］.传感技术学报，2014，27(1):123－127.

［15］朱敏，刘昊霖，张志宏，等.一种基于DV－HOP 改进的无线传感器网络定位算法［J］.四川大学学报:工程科学版，2012，44(1):93－98.

［16］单志龙，刘兰辉，张迎胜，等.一种使用灰度预测模型的强自适应性移动节点定位算法［J］.电子与信息学报，2014，36(6):1492－1497.