基于改进SURF 算法的双目视觉定位

韩 峰，李晓斌

(上海应用技术学院 电气与电子工程学院，上海 201400)

为了满足当今工业自动化不断发展的需要，机器人应运成为了自动化进程中的宠儿，与之相关的机器人技术也得到了前所未有的发展和重视，机器人视觉定位作为其中的一个重要技术分支，其精准度的提高成为了研究人员们努力的目标和方向。双目立体视觉定位因其具有较大的测量范围和较高的测量精度，成为机器人视觉定位中最常用的一种方法。在双目视觉定位中，对摄取的图像上特征点的提取以及提取到的特征点之间能否正确匹配，这两者决定着最终定位结果的精准度。SURF 算法是一种有效的特征点提取和匹配算法，它的高效率和高稳定性能均超越了同类算法［1］，所以本文采用SURF 算法对摄取的图像进行特征点的提取与匹配。由于SURF 算法本身存在的缺陷，在进行特征点匹配时容易产生特征点对的误匹配现象，为了消除误匹配，文中对SURF算法做了改进，加入了剔除误匹配点对的RANSAC 算法。实验结果表明，改进后的SURF 算法几乎实现了零误匹配，有效提高了双目视觉定位的精准度。

1 SURF 算法

SURF 算法是由H.Bay 等人在SIFT 算法的基础上，经过计算速度方面的改进，形成的一种快速特征提取与匹配算法［2］，该算法主要包括特征点的检测、特征点的描述以及特征点的匹配三大部分。

1.1 特征点检测

SURF 算法对特征点进行检测时加入了Hessian 近似矩阵以及积分图像［3］，这两者的加入在一定程度上使计算速度得到了提高。积分图像的定义如下:设X=(x，y)是所取图像I(X)上的任意一个像素点，则积分图像IΣ(X)就是取图像的原点为左上顶点、点X=(x，y)为右下顶点所组成的矩形区域里面的所有像素累加之和

这样，当把图像转换为积分图像时，就可以在积分图像内用一个简单的公式来计算矩形区域里面的灰度值之和，即ε=A－B－C+D，其中的A，B，C，D 分别是矩形4 个角的顶点。

SURF 特征点检测的依据是Hessian 近似矩阵行列式的局部极大值或者极小值所在位置。所取图像I(X)中的任意一个点X=(x，y)在尺度大小为σ 上的Hessian 近似矩阵定义为

式中:Lxx(X，σ)表示的意思是高斯二阶偏导在任意点X 处和所取图像I(X)两者之间的卷积，Lxy(X，σ)和Lyy(X，σ)具有相似的含义。为了提高整个过程的运算效率，Bay 等人将卷积结果用更简单的Dxx、Dxy和Dyy来分别代替Lxx，Lxy，Lyy，于是得到了Hessian 近似矩阵的行列式，即

式中:w 是一个一般取值为0.9 的权重系数。按照上面计算Hessian 近似矩阵行列式的方法，对所摄取图像上的任意点计算其响应并把结果保留下来，这样就会得到大小各不相同的σ 下的响应结果。然后从所得到的结果中，再进行非最大值抑制操作，于是那些极值点就可以挑选出作为候选特征点。最后，为了确保所选的特征点是真正的特征点，利用文献［4］中提出的3 维2 次函数拟合的方法，这种方法能够有效地对特征点进行精确定位，从而获取特征点的位置及不同大小尺度下的信息。

1.2 特征点描述

特征点描述的前提是对特征点进行主方向标定。以特征点为圆心做一定大小的圆形邻域，在邻域内，用Haar 小波模板对图像进行处理，使其得到x 和y 各自方向上的Haar 小波响应，再用一定大小角度的圆心角的扇形绕选定的特征点转一周，计算出该扇形处在任意一个角度时，图像上所有点的Haar 小波响应矢量之和，并从中找出长度值最大的那个，则它对应的这个方向就是该特征点的主方向。确定好主方向以后，就可以在主方向上构建描述向量了。以选定的特征点为中心，以一定的长度为边长做一个正方形邻域，将确定了的特征点的主方向设为正方形邻域y 轴的方向。将正方形邻域划分成多个子区域，用dx和dy表示每个子区域内x 轴、y 轴方向的Haar小波响应，并分别对每个子域内的求和，就会得到一个4 维向量，在对特征点进行提取时将会得到描述子特征向量，然后再对该向量进行归一化处理操作，这样，SURF 描述符就得到了。

1.3 特征点的匹配

设PA是所摄取图像A 上的任意一点，PB是摄取图像B上的任意一点，它们的描述子向量分别设为DA和DB。DA(i)和DB(i)分别是它们的第i 个分量，则PA和PB之间的距离为

按照式(4)进行计算，把A 图上某点PA(i)与B 图中的所有点之间的距离都计算一遍，然后再根据Lowe 在文献［5］中使用的最近邻比次近邻的方法进行匹配点的求取。

2 SURF 匹配算法的改进

在文献［6］中对SURF 算法所做的改进方法是一种基于图像的形态学处理基础的方法，该方法是通过对摄取图像中的目标物体进行形态学方面的处理，得到目标物体的边缘轮廓区域，然后再以边缘轮廓区域为基础建立积分图像，最后再进行SURF 算法图像匹配。这种改进算法虽然在一定程度上能够提高SURF 特征点提取的效率，但因为加入了平滑处理、边缘检测、膨胀处理以及进行闭运算等过程，还是会使整个过程所消耗的时间较长，并且由于该改进算法对识别特征点的敏感度不是特别高，在进行图像匹配的过程中也会少许存在特征点误匹配的现象。

针对SURF 匹配算法中存在的误匹配点对比较难剔除的问题，本文采用了加入用于剔除误匹配点对的RANSAC 算法对其进行了改进。RANSAC 是目前广泛应用于剔除误匹配点对的一种算法［7］。该算法的基本思想就是:对某个点集，给定一个几何约束模型，把符合这个约束模型的点作为所要寻找的内点保留，反之，不符合该约束模型的点作为外点剔除。在本文利用的算法程序的实现当中，加入的RANSAC 算法是基于一个基本矩阵几何约束模型的，该基本矩阵是对极几何的一种代数表示表达形式［8］。

图1 中展示的是对极几何的原理图。在三维视觉系统中，O 和O’表示两摄像机光心的位置，I1和I2表示两摄像机采集的图像，M 是三维空间中的任意一点，m 和m’分别是点M 在左右两图像中的投影点，点M、O 和O'三点所在的平面就是极平面，极平面与两左右图像之间的交线记为l1(me)、l2(m’e’)，所形成的这两条直线叫作极线。从上面展示的原理图中可以知道，m 点一定在极线l1上，而m’点也一定在极线l2上，所以m 点的对应点一定在图像l2中的极线l2上。不论M 点怎么改变，所形成的极线都会过极点e 和e’，这就是极限约束，它的代数表示形式就是基本矩阵。在求取该基本矩阵时，本文采用的方法是简单有效的8 点算法［9］，为了使利用的8 点算法估计出的基本矩阵精准度更高，在选取8个匹配点对之前，文中对SURF 提取的匹配点对集合中的点进行了坐标归一化处理。最后在剔除不满足条件的匹配点对时，使用了Sampson 距离判据法［10］。

图1 对极几何的原理图

现将加入RANSAC 算法剔除SURF 误匹配点对的整个改进算法的步骤总结如下:1)对利用原SURF 算法匹配出来的点对集合中的点进行坐标归一化处理操作。2)从匹配点对集合中任意取出8 个匹配点对计算其基本矩阵。3)用Sampson 距离判据法，将符合条件的匹配点对作为内点记录下来。4)重复2)、3)中的步骤n 次，并把每一次得到的符合条件的内点数记录保存下来。5)从中挑选最大的内点数，并计算出该最大内点数对应的基本矩阵，再根据Sampson 距离判据法，把匹配点对集合中所有符合条件的点对找出，并把它们确定为最终的内点，而将不符合条件的匹配点对剔除掉。通过上面的5 个步骤，就可以完成加入了RANSAC 剔除误匹配点对的改进SURF 算法。

利用原SURF 算法、经过图像形态学处理改进后的SURF 算法以及加入了RANSAC 算法改进后的SURF 算法对图像进行匹配，其对比结果如图2、图3、图4 以及表1 所示。

图2 原SURF 算法图像匹配

图3 经过图像形态学处理改进后的SURF 算法图像匹配

图4 加入了RANSAC 算法改进后的SURF 算法图像匹配

表1 SURF 及其改进后的匹配效果比较

从图表中可以看出，加入RANSAC 算法后的SURF 算法，在对图像进行匹配时，能有效剔除误匹配点对，使匹配的正确率几乎达到了100%，这就为后面双目视觉定位中的图像匹配提供了一个精准的算法环境。改进后的算法消耗的时间也比较少，都能够满足运算的实时性。

3 双目立体视觉定位原理

双目立体视觉定位的原理是，让两摄像机分别放在不同的位置，来获取同一个目标物体存在有视觉差的两幅图像，然后利用视差原理［11］计算出目标物体的空间三维几何信息，从而确定目标物体的空间位置。

图5 是平行双目立体视觉原理图，两摄像机投影中心点之间的距离是基线距，设为b。本文将两摄像机镜头的光心所在的位置定为摄像机坐标系的原点。左右两镜头的光心前f 处是左右两成像平面，O1uv、O2uv 是两图像坐标系，它的纵横坐标的方向与x 轴和y 轴方向一致，O1和O2是图像坐标系的原点，p1(u1，v1)和p2(u2，v2)是任意空间点P 的左右图像坐标点。两摄像机的光心距离两成像平面相同，则空间点P的左右两图像坐标的纵坐标Y 相同，即v1=v2，由几何知识可以得到

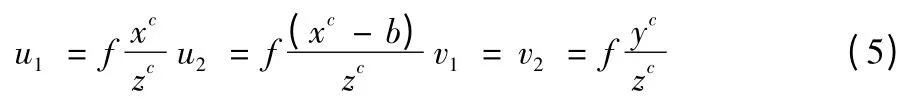
式中:坐标(xc，yc，zc)是空间点P 在左摄像机坐标系中的坐标;b 为基线距;f 是焦距，则视差即为点P 在两图像中相应点的位置差

由此，空间点P 在左摄像机坐标系中的坐标可以计算得到为

图5 平行双目立体视觉原理图

式中:zc=就是目标点P 的深度距离。在求取目标物体的三维坐标之前，要事先计算出摄像机的内外参数，然后再利用上面的公式就可以计算出目标物体的三维坐标，从而可以确定出该点的具体位置。

4 双目视觉定位的实验测定

实验采用两个型号为CM－323CDNP 的针孔摄像机，组成平行双目视觉系统，两摄像机的基线长为100 mm，CCD 芯片为1/3 in Sony CCD，靶面尺寸为宽4.8 mm×高3.6 mm，对角线的长度为6 mm，镜头的焦距f 为3.6 mm，获取到的图片大小为720×960 像素。

试验中，把篮球作为目标物体。将目标物体的模板图像分别与双目摄像机所拍摄获取的左右图像，用加入了RANSAC 算法改进后的SURF 算法进行匹配，匹配结果如图6、图7 所示。从匹配图中采集目标物体上的各个匹配点的坐标，然后对这些坐标求取平均值，所得的平均值就可以估计为目标物体在左右图像上的中心坐标点。再利用平行双目视觉原理中的式(5)、式(6)就可以计算出该点的深度距离，从而实现了对目标物体的定位。此次实验，求取的目标物体在左右图像上的中心坐标点分别是:(1 067，370)、(1 155，370)，通过计算得出目标物体的深度距离为509 mm，实际测量的距离是500 mm。然后在不同的实测距离下分别用SURF 算法、经过图像形态学处理改进的SURF 算法以及加入了RANSAC算法改进的SURF 算法进行多组实验，所得的结果如表2 所示，整个实验基于的仿真软件是MATLAB R2010a。

从表2 列出的结果中可以看出，基于经加入剔除误匹配点的RANSAC 算法改进后的SURF 算法的双目视觉定位更准确。但由于在双目视觉标定过程以及在求取摄像机内部参数时会存在一定的误差，再加上用匹配点对坐标的平均值来估计目标物体中心点坐标时存在的误差，所以计算结果会存在一定的偏差。

图6 目标物体与左图像的匹配

图7 目标物体与右图像的匹配

表2 基于SURF 及其改进后的测距结果 mm

5 结论

在双目视觉定位中，图像匹配是最核心，也是最关键的一步，特征点能否正确匹配，将直接影响着定位的准确度。SURF 算法作为一种在同类算法中，各方面优势都比较突出的算法，被广泛应用于图像特征点的提取与匹配中。SURF算法能够对绝大部分的特征点进行正确匹配，但由于客观因素的影响，它会对那些特征不明显的极少数特征点对产生误匹配，影响定位的准确度。为了达到消除误匹配的目的，文中对SURF 算法进行了改进，在原来算法的基础上加入了消除误匹配的RANSAC 算法。实验结果表明，改进后的SURF 算法几乎实现了零误匹配的效果，提高了双目视觉定位的准确度。

［1］HERBERT B，TINNE T，LUC V G.SURF:speeded up robust features［C］//Proc. 9th European Conference on Computer Vision.Graz，Austria:ECCV Press，2006:404－417.

［2］HERBERT B，ANDREAS E，TINNE T，et al. Speeded－Up Robust Features(SURF)［J］.Computer Vision and Image Understanding，2008，110(3):346－359.

［3］VIOLA P，JONES M.Rapid object detection using a boosted cascade of simple［C］//Proc. 2001 IEEE Computer Soeiety Conference on Computer Vision and Pattern Recognition. Kauai Marriott，Hawaii:IEEE Press，2001:511－518.

［4］BROWN M，LOWE D G.Invariant features from interest point groups［C］//Proc. British Machine Vision Conference，Cardiff，Wales，BMVC.［S.l.］:IEEE Press，2002:656－665.

［5］LOWE D G.Distinctive image features from scale－invariant key points［J］.International Journal of Computer Vision，2004，60(2):91－110.

［6］刘丹丹，魏维.一种改进的车头SURF 特征提取和匹配［J］.成都信息工程学院学报，2014(2):167－172.

［7］FISCHLER M A，BOLLES R C.Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography［J］.Communications of the ACM，1981，24(6):381－395.

［8］RICHARD H，ANDREW Z. Multiple view geometry in computer［M］.2nd ed.New York:Cambridge University Press，2003.

［9］HARTLEY R I.Estimation of relative camera position for uncalibrated cameras［C］//Proc.the 2nd European Conference on Computer Vision.Santa Margherita Ligure，Italy:ECCV，1992:579－587.

［10］YAN L W，ZHEN J M.Automatc panorama image mosaic and ghost e1iminating［C］//Proc.IEEE International Conference on Multimedia and Expo.Hannover，Germany:ICME，2008:112－115.

［11］高文，陈熙霖.计算机视觉—算法与系统原理［M］.北京:清华大学出版社，1999.