ZVS隔离型高增益DC/DC变换器
邾玢鑫,程 杉,谭 超
(三峡大学 电气与新能源学院,湖北 宜昌 443002)
0 引言
随着环境问题和能源危机的加剧,近年来新型清洁能源在世界范围内得到了快速的发展[1-4]。但如燃料电池、光伏电池板等新型能源的输出电压均较低,且输出电压也不规范。因此在其输出端口需要一个具备高升压能力的变换器,一方面将较低的电压升高到合适可用的电压等级,另一方面将不稳定的输出电压转化为稳定可靠的输出电压[5-7]。在一些对安全性要求较高的场合,如电动汽车或家庭式光伏发电中,利用高频变压器实现输入输出电气隔离也是必不可少的一部分[8-9]。总体而言,在该类应用场合中,高效、高可靠性以及高功率密度的隔离型高增益升压变换器已经成为一个研究热点[10-21]。
隔离型DC/DC变换器按照其变压器输入端电能输入形式可以分为电压输入型和电流输入型。不考虑变压器变比时,电压输入型具有降压、输入电流断续等工作特点。在高增益应用场合中,将进一步增加变压器原副边匝数比,此外由燃料电池和光伏电池的输出特性可知,采用该类型的变换器时,还需要较大体积的LC滤波器以保证电池输出电流的连续平滑,这无疑会给变换器的功率密度、成本以及效率带来不利的影响。因此在该类型的高增益变换场合中,采用电流输入型更有优势。常见的电流输入型拓扑可以归结为桥式、推挽式以及L式3种类型[10-11]。相比较而言,L式具备开关导通损耗小、变压器利用率高以及输入电流纹波小等优点,更适合于低压大电流输入的应用场合[12]。
为了在避免较高变压器匝比的情况下提高隔离型变换器的输入输出增益,文献[12-16]通过采用多个变压器及相应的整流电路,将多个变压器的输入端各自并联输入多个电流源,而次级的整流电路输出端串联在一起工作,得到的最终输出电压为各路整流输出电压之和,这显然可以获得较高的输入输出增益比。该方法的优点在于不仅可以有效提高输入输出增益,而且可以有效降低器件的电压、电流应力,以及开关损耗和电路的导通损耗;缺点在于使用过多器件会降低电路的整体可靠性,且控制及驱动电路的设计也较为复杂。文献[17-19]通过提高后级整流电路的增益来获得较高的输入输出比。与前一种方法相比,该方法具有元器件少、电路结构简单等优点,近年来所受关注也较多。文献[17-18]通过采用倍压整流电路获得了2倍的电压增益,但其所增加的增益倍数有限,且整流滤波电路中所用二极管的电压应力并未降低。文献[19]在传统倍压整流电路上,提出了一种4倍压整流电路,其进一步增加了输入输出增益比,且有效降低了二极管的电压应力,较适合于要求输入输出隔离的高增益应用场合。
前述方案虽然提出了多种具备高增益升压能力的整流电路,但其增益倍数均是固定不变的。文献[20]提出一种基于 DCM(Diode-Capacitor Multiplier)单元实现的非隔离型高增益DC/DC变换器,其输入输出增益可以通过设定DCM单元数来调节。本文进一步将该增益单元与L式电流输入型拓扑相结合,提出了一种ZVS隔离型高增益DC/DC变换器。文中以含有3个DCM单元的变换器为例,分别阐述其工作原理及性能特点,在此基础上讨论了变换器中关键参数的设计,并制作了一台输出功率为200 W的实验样机,对所述理论分析进行了实验验证。
1 工作原理
本文所提ZVS隔离型高增益DC/DC变换器拓扑如图1所示。图2为含有3个DCM单元的变换器拓扑。为简化其分析过程,下面均假设:①电感电流iL1、iL2连续;②电容 Co、C1、C2、C3足够大,其上电压保持不变;③所有器件都是理想器件,不考虑寄生参数等的影响;④箝位电容与漏感间的谐振周期远大于开关关断时间,且忽略箝位电容上的电压纹波;⑤有源开关VT1、VT2采用交错控制策略,而且开关占空比D>0.5;⑥辅助开关VTc1、VTc2与各自支路的主开关互补导通,且主开关与相应的辅助开关在切换时留有足够的死区时间。
在一个开关周期Ts内,变换器有21个等效工作电路,各状态稳态工作时的主要波形如图3所示(图中 D=0.7)。其中 DVT1、DVT2、DVTc1、DVTc2分别表示开关 VT1、VT2、VTc1、VTc2的占空比波形。下面具体介绍变换器稳态工作时的开关状态。
(1)状态 1(t0~t1)。该状态中,主开关 VT1、VT2均导通,电感电流iL1、iL2在输入电源uin的激励下线性上升;变压器次级二极管 VD0、VD1、VD2、VD3均反向截止,辅助开关 VTc1、VTc2均关断,箝位电容 Cc1、Cc2上的电压均保持不变,输出滤波电容Co独自向负载供电,输出电压uo下降。
(2)状态 2(t1~t2)。在 t1时刻主开关 VT2的驱动信号关断,主开关VT1保持导通,电感电流iL1在输入电源uin的激励下继续线性上升;电感电流iL2向开关VT2的漏源极电容CVT2充电,由于电容CVT2的存在,限制了开关VT2漏源极电压的上升速度,可以有效降低开关VT2的关断损耗;该过程持续到电容CVT2上的电压上升至uo/(4N)结束,其中N为变压器变比。
(3)状态 3(t2~t3)。在 t2时刻开关 VT2漏源极电容 CVT2上的电压上升至 uo/(4N),二极管 VD1、VD3导通,漏感电流iLk开始上升,但由于漏感Lk的存在,iLk上升速度受限,因此二极管VD1、VD3实现了近似零电流导通。电感电流iL1继续为电容CVT2充电,该过程持续到电容CVT2上的电压上升至uCc2结束。由于电容CVT2非常小,所以从漏感电流开始上升到电容CVT2端电压为uCc2的过程很短,因此在电路性能分析时可以忽略该过程的影响,认为漏感电流iLk上升的时刻与电容CVT2端电压被电容Cc2箝位的时刻一致。

图1 所提ZVS隔离型高增益DC/DC变换器拓扑Fig.1 Topology of proposed ZVS isolated high step-up DC/DC converter

图2 含有3个DCM单元的电流输入ZVS隔离型高增益DC/DC变换器拓扑Fig.2 Topology of current-fed ZVS isolated high step-up DC/DC converter with 3 DCM cells

图3 静态工作时一个开关周期Ts内的主要波形Fig.3 Main waveforms within one switching period Ts in steady-state operation
(4)状态 4(t3~t4)。在 t3时刻电容 CVT2端电压上升至uCc2,辅助开关VTc2的体二极管导通,由于箝位电容Cc2相对电容CVT2来说很大,因此大部分电感电流iL2将流入箝位电容Cc2中,开关管VT2漏源极电压被箝位在uCc2,且从此刻开始漏感Lk、箝位电容Cc2以及变压器次级电容将会形成一个谐振电路,由于变压器次级电容设计时足够大,其电压纹波可以忽略,因此在分析其谐振过程时可以等效为一个恒定的电压源。这个谐振周期与漏感Lk和箝位电容Cc2的值有关(忽略电容CVT2的影响),且谐振周期必须足够大,以保证电路的可靠工作[19]。该谐振过程会持续到t4时刻(辅助开关VTc2驱动信号到来)结束。
(5)状态 5(t4~t5)。在 t4时刻辅助开关 VTc2的驱动信号到来,因其体二极管已提前开通,故辅助开关VTc2实现零电压开通;该状态下漏感电流iLk近似线性上升,该过程持续到iLk上升至电感电流iL2时结束。
(6)状态 6(t5~t6)。在 t5时刻漏感电流 iLk上升至电感电流iL2,箝位电容电压uCc2停止上升并开始向漏感Lk进行放电,漏感电流iLk继续上升,该过程持续到辅助开关VTc2关断时结束。
(7)状态 7(t6~t7)。在 t6时刻辅助开关 VTc2的驱动信号关闭,电容CVT2的存在限制了开关VTc2端电压的上升速率,可以有效降低开关VTc2的关断损耗,之后箝位电容Cc2退出谐振电路,此时仅余开关VT2漏源极电容CVT2独立向漏感Lk谐振放电,该状态持续到电容CVT2上电压下降至uo/(4N)结束。
(8)状态 8(t7~t8)。在 t7时刻电容 CVT2上的电压下降至uo/(4N),漏感Lk端电压反向,漏感电流iLk达到最大值并于此刻开始下降,电容CVT2通过漏感Lk继续放电,该过程持续到电容CVT2上的电压下降至0。
(9)状态 9(t8~t9)。在 t8时刻电容 CVT2上电压下降至0,主开关VT2的体二极管导通,漏感Lk端电压为 -uo/(4N),漏感电流iLk线性下降,电感电流 iL1、iL2在输入电源uin的激励下线性上升;该过程持续到主开关VT2的驱动信号开通时结束。
(10)状态 10(t9~t10)。在 t9时刻主开关 VT2的驱动信号开通,由于其体二极管已经导通,主开关VT2实现了零电压开通,漏感电流iLk继续线性下降,该过程持续到漏感电流iLk下降至电感电流iL2时结束。
(11)状态 11(t10~t11)。在 t10时刻漏感电流 iLk下降至电感电流iL2,主开关VT2的电流在此时反向,该过程持续到漏感电流iLk下降至0时结束。变压器次级二极管VD1、VD3的电流也随之下降至0。值得注意的是,受漏感电流iLk下降速率的控制,二极管VD1、VD3的电流下降速率也得到了有效控制,实现了近似零电流关断,可以有效降低二极管的反向恢复损耗。在 t10时刻之后,次级二极管 VD0、VD1、VD2、VD3均反向截止,主开关 VT1、VT2均导通,电感电流 iL1、iL2在输入电源uin的激励下线性上升,与状态1一致。
主开关VT1、辅助开关VTc1的开关切换状态与主开关VT2、辅助开关VTc2的开关切换状态相似,在此不再赘述。
2 性能分析
根据上述4倍于普通L型升压变换器的工作原理,下面对其进行性能分析,并将分析结果推广到含有m个DCM升压单元的L型升压变换器中,以便根据输入输出参数进行设计。在以下分析过程中进行如下简化:开关均采用交错控制策略,且开关占空比D>0.5,并假定所有电感电流均连续,忽略寄生参数的影响及电容上的纹波。下面分别从输入输出增益、电压和电流应力及各相输入电流间的关系方面进行性能分析。
2.1 输入输出增益
忽略漏感以及主开关与有源箝位开关之间死区时间的影响,由电感L1、L2的伏秒平衡可得:
化简可得:

推广到含有m个DCM升压单元的L型升压变换器中可得输入输出增益M为:

图4所示为不同DCM单元数m及变压器变比N下,输入输出增益M关于占空比D的函数。可见通过增加DCM单元数和变压器的匝比均可显著提高变换器的输入输出增益。

图4 输入输出增益与变压器匝数比、DCM单元数及占空比之间的关系Fig.4 Curve of conversion ratio vs.duty cycle for different turn-ratios and DCM cell numbers
2.2 开关器件的电压应力
忽略箝位电容上的电压纹波、电感电流纹波(电感电流记为IL)以及主开关与有源箝位开关之间死区时间的影响,由前述分析可知,开关器件的电压应力即为箝位电容上的电压峰值。因此此时仅需计算箝位电容上的电压值即可。由电源输入功率和变压器输入功率平衡可得(忽略中间损耗的影响):

由于忽略了箝位电容上的电压纹波以及主开关与有源箝位开关之间死区时间的影响,因此可以认为漏感电流iLk是线性上升的:

通过式(4)和式(5)可以解得:

将式(3)代入式(6)进行化简可得:

可以看出箝位电容电压由两部分构成:一部分是忽略漏感时理想状态下的开关管的电压应力;另一部分和漏感大小直接相关,随着漏感值的增加而增加。因此在保证电路正常工作时,漏感值应越小越好。值得注意的是,由于箝位电容上电压纹波的存在,实际开关管的电压应力要略高于式(6)计算的结果。推广到含有m个DCM升压单元的L型升压变换器中可得箝位电容上电压为:

定义二极管 VD0、VD1、VD2、VD3的电压应力 uvpVD0、uvpVD1、uvpVD2、uvpVD3,根据电路工作原理易知:

推广到含有m个DCM升压单元的L型升压变换器中可得:

2.3 开关管及二极管的电流应力
忽略漏感以及主开关与有源箝位开关之间死区时间的影响,忽略电感电流纹波,设它们的值分别为IL1和IL2。同样忽略输入电流iin的纹波,设其值为Iin。根据电容C3的安秒平衡可得:

由式(12)可知,电感电流实现了自动均流,无需采用任何有源均流策略。
设开关管电流iVT1、iVT2的平均值分别为IVT1和IVT2,二极管电流 iVD0、iVD1、iVD2、iVD3的平均值分别为IVD0、IVD1、IVD2、IVD3。根据变换器工作原理,流过开关管的电流平均值分别为:
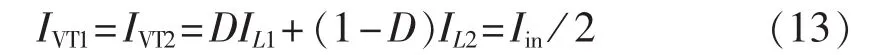
由于正常工作时电容电流平均值为零(电容的安秒平衡),于是可得:
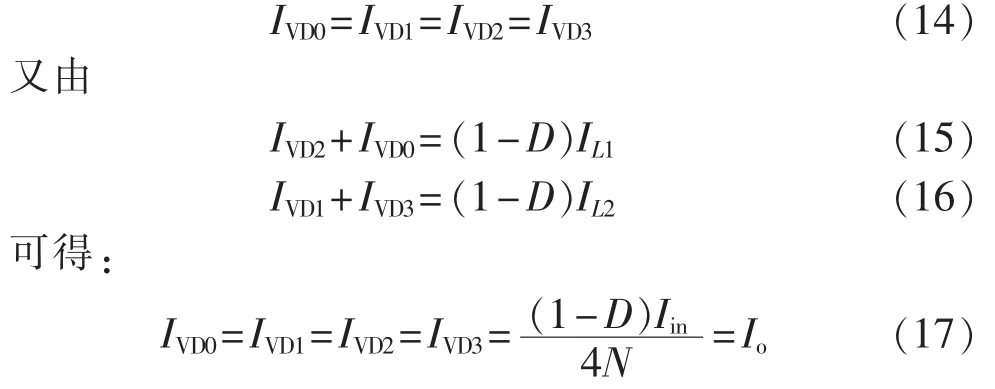
通过类似推导,对于含有m个DCM升压单元的L型升压变换器,当m是奇数时,电感电流及流过开关管和二极管的电流平均值分别为:

当m是偶数时,电感电流及流过开关管和二极管的电流平均值分别为:
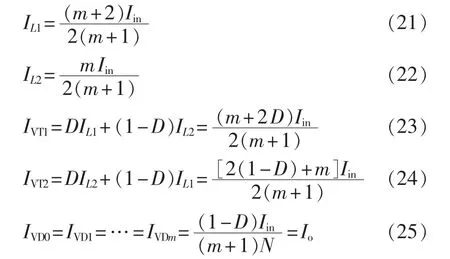
通过上述分析可知,次级二极管的电压应力和电流应力均相等,开关管的电压应力一致,电流应力在DCM单元m是奇数时一致,为偶数时近似一致。这意味着这些器件的损耗基本一致,有利于器件的选择和散热器设计。
3 关键参数设计
在进行仿真和实验之前,首先应该设计出满足变换器工作要求的电路参数,因此本节中对影响变换器工作性能的几个关键参数进行设计指导。
3.1 变压器变比
前级采用L型结构,开关占空比需满足D>0.5,在根据输入输出电压变化范围可以确定变压器变比N(N=n2∶n1)的上限,另一方面变压器变比直接关系到原边反射电压的大小,较小的原边电压可以获得较小的开关电压应力。因此可通过设定最小的占空比D来确定变压器变比,如式(26)所示。

其中,m为后级增益单元数。
3.2 漏感值
通过第2节的分析可知,漏感值与箝位电容上的电压满足式(8)。因此在不考虑其他因素的前提下,总是希望漏感值越小越好。但由第1节中的分析可以看出,漏感在辅助开关关断之后必须保证足够的能量去完成开关漏源极电容的放电,从而保证主开关的零电压导通。因此可得式(27)。

3.3 箝位电容
漏感值确定之后,通过设定箝位电容的值可以设定箝位电容与变压器漏感之间谐振工作的谐振周期;由变换器在开关管关断之后的谐振工作过程不超过该谐振周期的一半可以得到式(28)[19]。

值得注意的是,谐振电容取较大值可进一步降低箝位电容上的电压纹波,以降低开关器件上电压应力。通过前述理论分析可知,过大的箝位电容不会影响电路的其他性能,故可以式(28)为下限,考虑变换器的功率密度后选择合适的箝位电容值。
4 实验研究
为验证前述理论分析的正确性和有效性,搭建了一台实验样机,其参数如下:输入电压uin=24 V;输出电压uo=400V;最大输出功率Po=200W;开关频率fs=100kHz;有源开关 VT1、VT2、VTc1、VTc2采用 IPP110N20N3G;二极管 VD0、VD1、VD2、VD3采用 STTH15L06;箝位电容Cc1=Cc2=10 μF;有源开关端电容 CVT1=CVT2=6.6 nF;增益单元电容C1=C2=2.5 μF;增益单元电容C3=5μF;输出滤波电容 Co=20 μF;输入电感 L1=L2=200 μH;实测漏感值 Lk=2.69 μH;变压器变比 N=n2∶n1=12∶7。
实验结果如图 5所示,通过图 5(a)—(d)可以看出所有开关均实现了零电压导通,开关损耗得到了有效降低。同时图 5(e)与图 5(a)、(b)比较可见,主开关漏源极端电压应力被有效控制在箝位电容Cc1、Cc2的端电压附近。最大电压尖峰不超过90 V,箝位电路有效限制了由变压器漏感引起的电压尖峰。
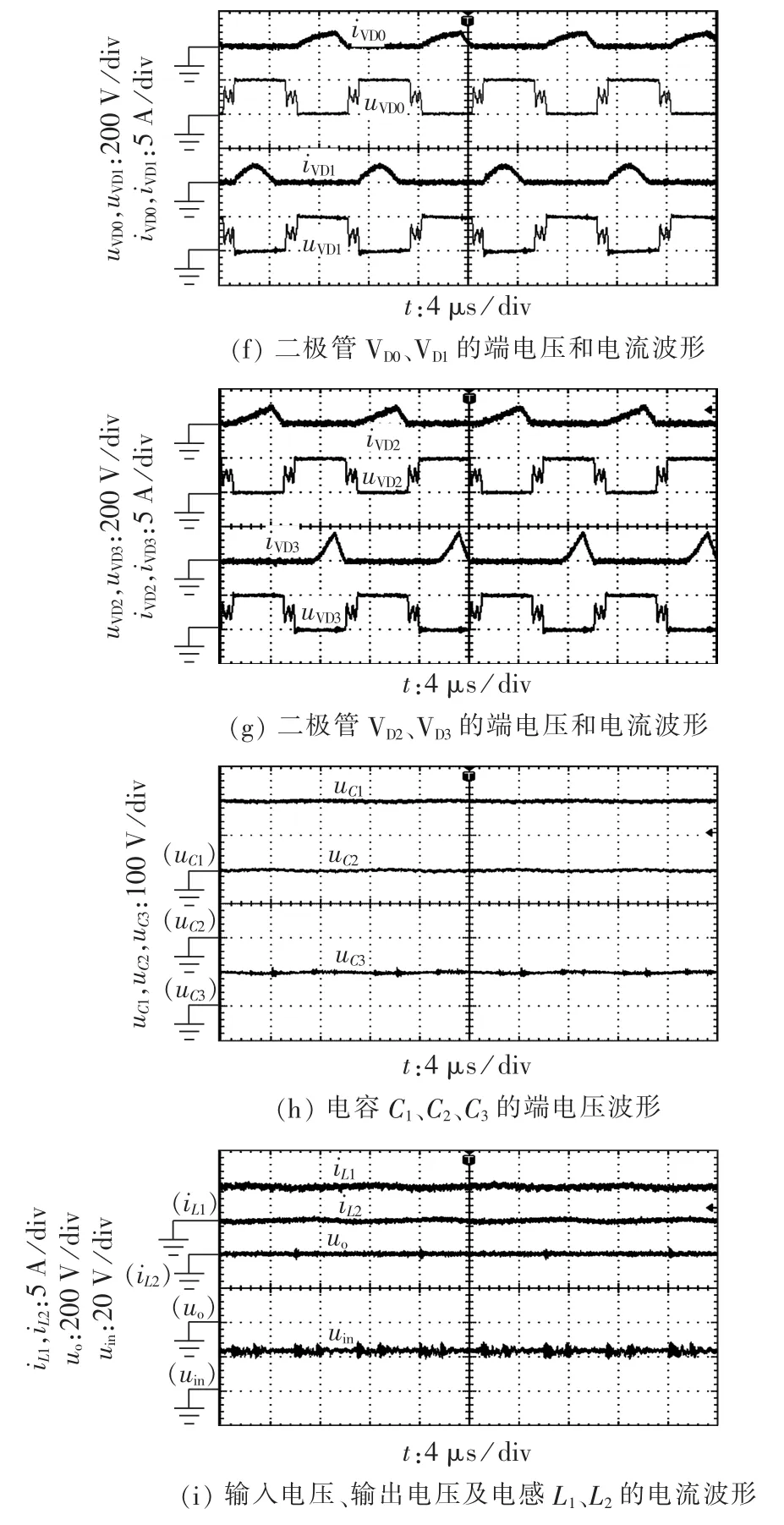
图5 实验波形Fig.5 Experimental waveforms
从图 5(f)、(g)可见变压器次级二极管 VD0、VD1、VD2、VD3的电压应力均约为200 V,电流有效值相等,所有二极管均实现了零电流关断,几乎没有反向恢复电流的存在。从图5(h)可见电容C1、C2的端电压uC1、uC2约为200 V,电容C3的端电压uC3约为 100 V,与理论分析一致。
图5 (i)为输入电压uin,输出电压uo及电感电流iL1、iL2的波形,理论分析中此时主开关占空比约为0.6;由图 5(a)、(b)可知实际工作时主开关占空比约为0.65,与理论分析较为接近。
图6所示为实测的样机工作效率,其中最大工作效率约为95.2%,额定工作时效率约为93%。

图6 效率曲线Fig.6 Curve of efficiency vs.load

表1 损耗分析Table 1 Power loss analysis
表1 是通过理论分析得到的额定工作时变换器的损耗分布,考虑到所有开关均实现了零电压导通且二极管实现了零电流关断,因此忽略了开关损耗和反向恢复损耗,同时为简化分析过程,不考虑开关管的驱动损耗。显然,主要损耗集中在开关管和二极管的导通损耗、电感的损耗以及变压器的损耗上。理论分析得到的变换器额定工作效率为95.37%,与实际测量得到的93%相差较小。
5 结论
本文将L式电流输入型拓扑与DCM单元相结合实现了一种具备软开关能力的高增益隔离型DC/DC变换器,该变换器在实现高增益的同时,避免了DCM单元电压调节能力差的问题,同时通过箝位电路限制了变压器漏感导致的开关管电压应力尖峰,并实现了开关管的零电压导通和二极管的零电流关断。文中分析了变换器的工作原理并给出了关键参数的设计方法,理论分析和实验结果均表明所提变换器较适合于需要输入输出隔离的高增益变换场合。

