感生电动势的理解与应用

董友军

摘 要：笔者细读《物理教师》2014年第4期《一例有关感生电动势计算的讨论》原文，发现文中存在一些错误，通过分析错误原因，得出了正确结论，并用正确结论解析了一道教材题、一道高考题和一道模拟题。

关键词：法拉第电磁感应定律；感生电动势；欧姆定律；麦克斯韦电磁场理论

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2015）8-0070-3

《物理教师》2014年第4期上刊登了沈老师的一篇文章——《一例有关感生电动势计算的讨论》，笔者认真拜读多遍，发现沈老师对感生电动式的理解和应用存在不当之处。在写论文前，笔者把原文题目发在《物理教师》《物理通报》《物理教学探讨》《中学物理教学参考》《物理之友》的QQ群上讨论，发现很多老师也存在相同的不当观念。电磁感应是高考的必考点，感生电动势的应用常在高考物理试卷中出现。笔者认为有必要纠正教师中存在的不当观念，避免在高中教学中传播，以免影响学生的高考。

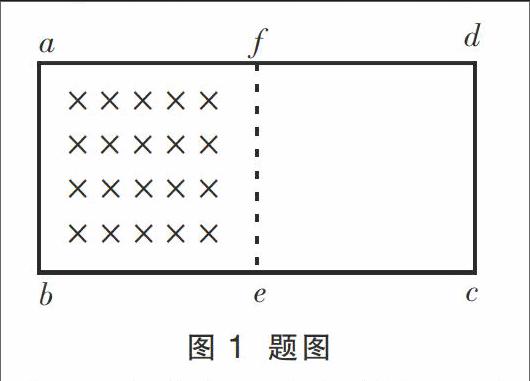
沈老师文章的原题如下：如图1，用均匀导线做成矩形线框abcd，且bc=2ab，ab=0.2 m，线框的左半部分放在垂直纸面向里的正方形区域匀强磁场中。当该磁场以10 T/s的变化率均匀增加时，求线框e、f两点的电势差的大小。

纵观全文，笔者认为沈老师有以下四个观点值得商榷：

1.感生电动势在线圈上是如何分布？

沈老师认为，“左半部分存在磁场而将其视作等效电源，右半部分不存在磁场，将其视作外电路”的观点是“不科学的”，进而得出自己的正确结论：“整个线圈都会产生感应电动势”，“右半部分为总电动势的1/4，左半部分为总电动势的3/4”。笔者认为，前面两种观点都是不科学的，正确的理解为：变化的磁场产生涡旋电场，线圈在涡旋电场作用下产生感生电动势，感生电动势分布在整个线圈上。若为闭合线圈，无论线圈是全部在磁场中还是部分在磁场中，感生电动势会分布在整个闭合线圈上，而不能理解为在磁场中那部分的线圈分布的电动势大，不在磁场中部分的线圈分布的电动势小。如图1，线圈的电阻均匀分布，若产生的感应电动势为E，则E均匀分布在闭合线圈abecdfa中，不是E只分布在fabe中而ecdf中没有电动势，也不是fabe中为3E/4而ecdf中为E/4。若为不闭合线圈，无论线圈是全部在磁场中还是部分在磁场中，感生电动势都是分布在整个不闭合线圈上的，而不能理解为在磁场中的部分线圈分布的电动势大，不在磁场中的部分线圈分布的电动势小。如图2，设电动势大小为E，E是均匀分布在不闭合线圈fabe中。如图3，设电动势大小为E，E是均匀分布在不闭合线圈dfabec中，不是E只分布在fabe中而df、ec中没有电动势。

2.如何正确理解麦克斯韦电磁场理论？

人教版《物理 选修3-4》中对麦克斯韦电磁场理论表述如下：变化的磁场产生电场，变化的电场产生磁场。

正确理解为：正弦变化的磁场产生正弦变化的电场，其产生的正弦变化的电场又会产生正弦变化的磁场，不断循环下去，就形成了电磁波，如人教版《物理 选修3-4》的图4。而均匀变化的磁场产生稳定的电场，产生的稳定的电场不再产生磁场，不能形成电磁波。

沈老师认为“右半线圈里虽然看似没有磁场通过也无磁通量产生，但左侧变化的磁场在右侧空间也要产生感生电场，右侧线圈里的自由电荷也会定向移动，该侧线圈中也要产生感应电动势”。

笔者认为，左侧变化的磁场是均匀变化的有界磁场，故在与有界磁场垂直的区域产生稳定的电场强度大，有界磁场以外的区域的电场强度小，高中阶段应该忽略不计。否则，任何一个有关感生电动势的习题都无法解答，如人教版《物理 选修3-4》的图5。所以，右侧线圈有感生电动势不是“左侧变化的磁场在右侧空间也要产生感生电场”而产生，而是左侧变化的磁场产生的感生电动势要分布在整个线圈，右侧线圈才有感生电动势。

3. 感生电动势公式E=nS中S的含义是什么？

沈老师认为，S为“线框在磁场中的面积，为线框的有效面积”，却没有说明什么是“有效面积”。笔者认为，当磁场和线圈垂直时，有效面积应该是磁场区域与线圈区域重叠的面积。如图6、图7、图8中，S应该为abcda的面积，不是线圈的面积，也不是磁场的面积。

4.感生电动势电路中两点间电势差用什么公式？

沈老师求解e、f两点的电势差用“Uef=Eebaf-IRebaf”。笔者认为，因为感生电动势均匀分布在线圈上，所以两点的电势差应该理解为电阻产生的电压降，即应该用部分电路欧姆定律求得。如原题e、f两点的电势差，应该理解为顺着电流方向的电压降，用部分电路的欧姆定律的公式求得，即Uef=IRef。

根据以上分析，原题正确解答：

步骤1：根据楞次定律，判断感应电流方向为逆时针。

步骤2：由E=S可得闭合线圈abecdfa中的感应电动势为E=0.2 m×0.2 m×10 T/s=0.4 V。

步骤3：设ab边的电阻为r，线圈的总电阻为6r，由闭合电路的欧姆定律得总电流为I=E/6r。

步骤4：Uef=I·3r=0.2 V。

有关感生电动势的习题非常多，教科书、高考卷、模拟卷上都会有。在解题时，一定要注意感生电动势是分布在整个线圈上，这样才可以正确理解电路结构，分清多个电阻的连接是串联还是并联关系，从而求得闭合电路的总电阻，再用闭合电路欧姆定律得出电路的总电流。现在各举一例，体验在有关感生电动势的习题中如何解析。

应用1 教材题：（“人教版”选修3-2第四章第5节习题）如图9甲，100匝的线圈（图中只画了2匝）两端A、B与一个电压表相连，线圈内有磁场，线圈中的磁通量在按图乙所示规律变化。

（1）电压表的读数应该等于多少？

（2）请在线圈位置标出感应电场的方向。

（3）A、B两端，哪端应该与电压表标+号的接线柱（或红接线柱）连接？

解析

（1）由乙图可得=0.5 Wb/s，由E=n=100×0.5 V=50 V，因为A、B断开，此时电压表测量的电压等于电动势，即电压表的读数等于50 V。

（2）根据楞次定律可得，感应电场的方向为逆时针方向。

（3）因为感应电场的方向为逆时针方向，即A端的电势高，B端的电势低，则A端应该与电压表标+号的接线柱连接。

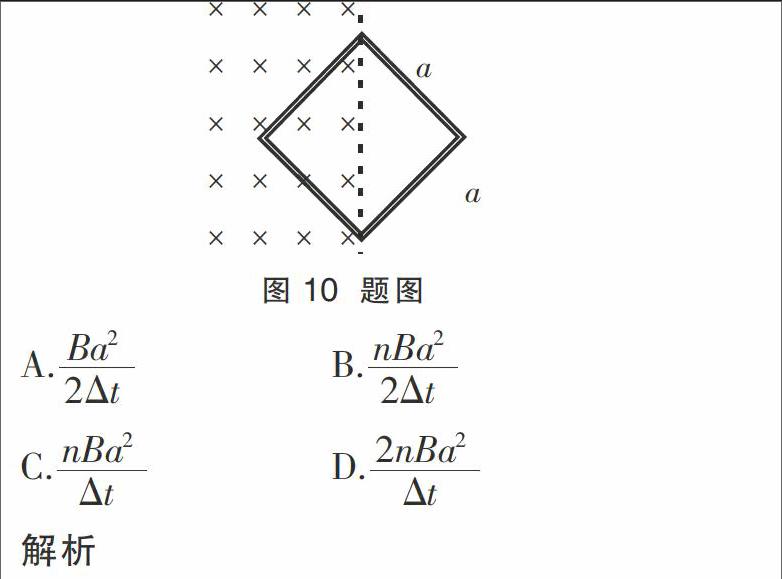
应用2 高考题：（2014年江苏高考物理卷）如图10所示，一正方形线圈的匝数为n，边长为a，线圈平面与匀强磁场垂直，且一半处在磁场中，在 Δt时间内，磁感应强度的方向不变，大小由B均匀地增大到2B，在此过程中，线圈中产生的感应电动势为（ ）

A.R1中的电流方向为M→R1→P，R2中的电流方向为B→R2→A

B.电压表的示数为0.3 V

C.R1的电功率为0.045 W

D.0～0.2 s内R3中通过的电荷量为0.3 C

参考文献：

[1]沈海辉.一例有关感生电动势计算的讨论[J].物理教师，2014，35（4）：63—64.

[2]普通高中课程标准实验教科书·物理·选修 3-2[M].北京：人民教育出版社，2004：21.

（栏目编辑 邓 磊）