在不规则图形问题中巧用平移

江炜杰

其实，我们在小学时就已经跟平移有所接触了.初学平移，感觉平移问题就是画平移的图形.其实平移也是一种数学方法.

我们有时会碰到有关不规则图形的问题，这时通过平移构造规则图形，就可使问题简单化.

例1如图，在长为50m，宽为30m的长方形地块上，有纵横交错的几条小路，宽均为1m，其他部分均种植青菜，求种植青菜的面积.

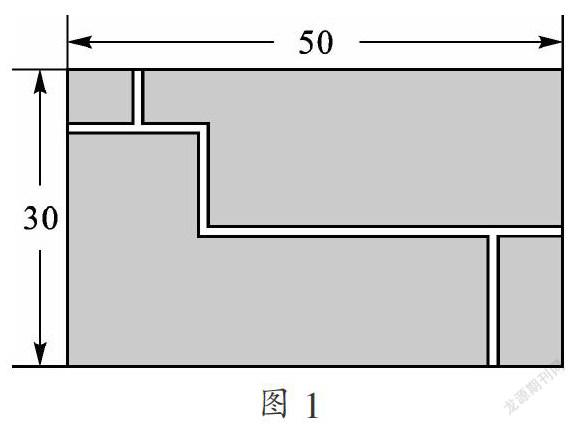
首先很容易想到，直接求是行不通的.分割的方法就算可以，也很麻烦，还可能导致算错.所以我们这时候就不能局限于原图形了，试试平移吧.可以看到大长方形被小路分成了四块图形，只要把这四块图形拼到一起，就可以拼成一个矩形，至于怎么拼也不用多说了，很简单.再结合小路宽度为1m，计算出拼合矩形的长和宽，最后求出面积.

例2 如图，求图形的周长

这个不规则图形倒是挺“规则”的，是一个类似于领奖台的图形.首先图形大部分都由折线构成，但一条折线的数据都没有，就算它们都是相等的也没用.这样不由得就要联想到：如果这些折线能连成一条线段就好了.使折线拼成线段？于是就又联想到了平移的知识了，只要我们把横线段和竖线段分别移到最上面和最两边（如图的箭头），那就又变成一个矩形了，周长也就可以算了.这样利用10和16这两个数据马上可以算出周长为52

例3 如图是山西省某古宅大院窗棂图案：图形构成10×21的长方形，空格与实木的宽度均为1，求这种窗户的透光率.（即空格面积与全部面积之比）

这显然又不能直接求空白面积，而且图形比上两题更为复杂.可能有人会想到把它分成一个一个长方形来求，我只能用一个字来说：烦！大量的算式还可能导致计算错误，那么就要看看该怎么平移来改变原图了.首先看清楚这个图形，眼睛千万不要被它绕晕了.仔细看清楚这个问题的图中的两个空白部分，你肯定会发现其实这两个“回”字形图形是由其中一个旋转180°得来的，通俗地说，就是一个倒过来变成另一个，那问题就好办了，把左边的空白部分向右平移，需要注意的是，还要再向下平移1格才能覆盖住右边的实心部分.就可以拼合成一个矩形，然后回到题目要求，就要知道这个矩形的长和宽才能求面积.不难想到是“空格与实木的宽度均为1”来求，数一数这个矩形的长和宽分别由几条空白或实心构成，最后求出面积，面积为90.全部面积为10×21=210，所以透光率为90：210=3：7.

由上面的几道小例题可以说明，学习平移，就要有应用它来解决问题的主动意识.平移是一种数学方法，我们应该主动去调用它解决问题！

（指导老师：浦长宇）