挠性航天器浮动质心动力学建模

杨一岱，荆武兴，刘 玥

(哈尔滨工业大学航天工程系，150001哈尔滨)

随着空间技术逐步发展，航天器承担的任务日益复杂，很多任务需要借助带有较大挠性的附件来完成，如太阳帆板的对日定向，大型天线的对地或对其他星体的定向，有效载荷对空间中某方位的精确指向，空间机械臂灵活运动等［1-3］.在现代航天任务中，为减小发射质量，此类附件通常采用轻质的新型材料，故具有较大的尺寸和较小的质量，致使现代航天器整体结构趋于挠性化［4-5］.此类带有大挠性附件的航天器具有复杂的动力学特性［6］，附件的挠性振动与航天器的姿态、轨道运动之间相互耦合，在对此类航天器的动力学问题，特别是高精度控制问题进行研究时，须对挠性附件带来的影响进行详细分析.为此如何建立一套能精确反应航天器真实动力学特性的模型就成为一个重要课题.

在大挠性航天器的动力学建模方面，不少国内外学者进行了相关的研究.在早期的研究中，常采用分布参数法［7］(distributed parameter)和集中参数法［8］(lumped parameter).分布参数法可精确描述对象的动力学特征，但具有不易求解的缺点;集中参数法物理意义清晰明了且易于求解，但是其模化精度较低，不能满足工程需要.随着计算机水平的发展，现阶段最常用的手段是有限元法［9-10］.由于有限元法将整个系统结构看成由有限个用节点连接起来的小单元组成，在理论上单元可无限细分，使其模化精度可任意逼近，且便于计算机编制程序进行计算，从而成为当前工程上最常用的手段.在我国的航天控制领域中，也有大量学者对大挠性航天器的动力学建模问题进行了研究［11-13］.其中，屠善澄［14］提出一种基于有限元法的姿态动力学模型，对航天器姿态控制在工程实践方面具有很大的指导意义.但是，该模型是建立在卫星结构坐标系上的，而卫星于实际在轨飞行过程中，由于挠性附件振动的影响，其真实质心在其结构坐标系中是不断变化的，这就导致应用此动力学模型描述卫星姿态、轨道运动时会产生一定的误差.此外，由于卫星的轨道运动状态通常情况下都是以其质心的运动描述的，若姿态动力学的参考坐标系原点与卫星质心存在相对运动，对于描述卫星姿轨间的耦合作用也是不利的.随着工程实践中对精度指标的要求日益提高，已有的模型将不再满足新的任务需求.基于以上原因，本文建立了适用于大挠性卫星高精度姿态控制的浮动质心动力学模型，可用于定量分析卫星附件的挠性振动对卫星整体的姿态、轨道耦合作用，对实际工程应用具有一定的参考价值.

1 浮动质心模型

本文为建立适用于大挠性卫星的高精度姿轨耦合控制的动力学模型，不同于建立在结构坐标系上的传统的挠性卫星姿态动力学模型，将卫星姿态动力学模型建立在卫星实际质心上，其相对于结构质心是浮动的，称之为浮动质心.下面首先建立浮动质心的动力学模型，其中坐标系定义如下:oexyz为地心赤道惯性坐标系，原点oe为地心，oex轴指向春分点，oez轴指向北极，oey轴与其余两轴成右手系;obxbybzb为本体坐标系，原点ob为卫星实际质心，三轴与卫星的安装坐标系重合.

假设飞行器由一个中心刚体B和m个一端与其相连的挠性附件Bi(i=1，2，3)构成，如图1所示.其中P为挠性附件未变形时整星的质心，下称结构质心;ob为挠性附件变形后整星的质心，下称实际质心;rpi为第i个挠性附件与中心刚体的连结点相对于P点的位置矢量.

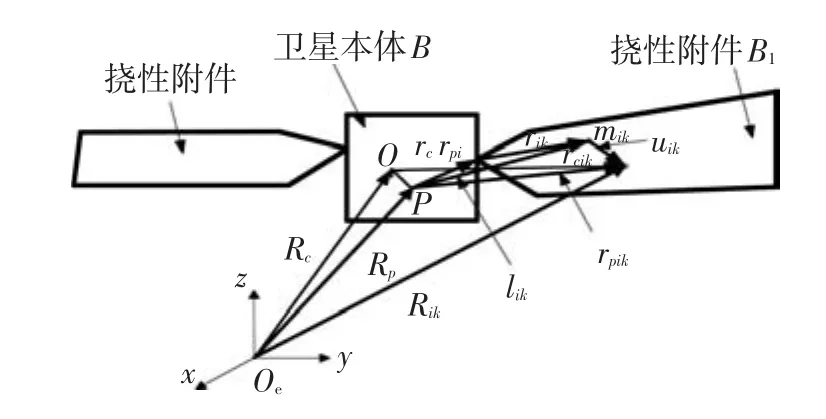
图1 由中心刚体和多个挠性附件构成的飞行器与坐标系

由图1中几何关系可知，飞行器质心浮动位移为

根据牛顿第二定律，对飞行器上任一微元mik(第i个附件上的第k个节点)有

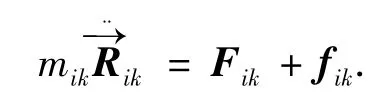
其中Fik、fik分别为mik所受外力、内力之和，对整星所有质量元求和，并结合牛顿第三定律(fik总和为0)与几何关系可得

又由质心定义结合牛顿第二定律有

将式(2)代入式(1)并将矢量做进一步分解可得

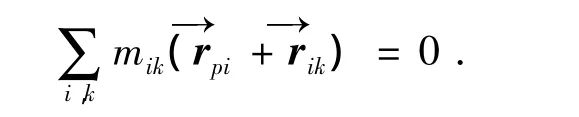
于是由式(3)最终可得到

式(4)为整星的质心位置变化与挠性附件形变的关系，即浮动质心模型.应指出，该模型描述的质心浮动位移项为航天器真实质心相对于其结构质心的位移，在实际情况下，由于挠性振动引起作用均为内力，并不会改变整个航天器的实际质心位置，真正在不断进行浮动运动的是航天器的结构质心.而航天器上的元器件和执行机构均是安装在结构坐标系下的，因此从观测的角度讲，就像是航天器的实际质心在相对其结构浮动运动.此外，对于航天器整体而言，实际质心的运动为长周期的慢变的轨道运动，结构质心相对于实际质心的晃动就是航天器受挠性振动激发的轨道耦合运动.显然，将姿态动力学模型建立在实际质心上更符合客观运动规律，且更易于描述航天器姿态与轨道之间的耦合效应.

2 姿态动力学方程

下面基于第一节给出的浮动质心模型推导航天器姿态动力学方程，由角动量定义可知

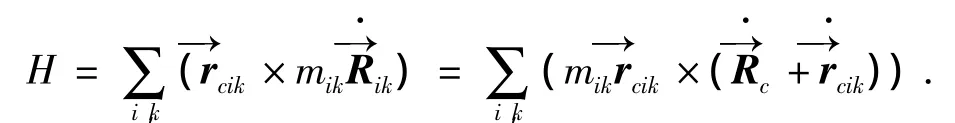
由质心定义并结合式(3)可知

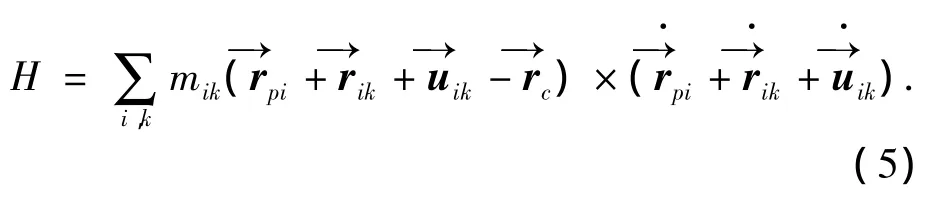
假设飞行器本体以角速度ω在惯性空间中旋转，挠性附件Bi以角速度ωi相对于飞行器本体旋转，由相对微分公式可知

将式(5)～(7)联立，经过详细推导化简最终可得

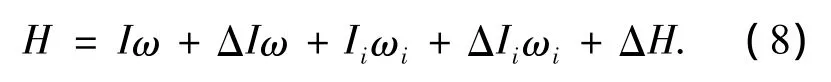
其中:Ⅰ为附件未变形时整星的转动惯量;ΔⅠ=ΔⅠc+ΔⅠu+ΔⅠcu，为由挠性变形和整星质心浮动共同引起的整星转动惯量改变量;，为仅由质心浮动引起的转动惯量改变量;，为仅由挠性变形引起的转动惯量改变量;，为挠性变形和质心变化耦合作用引起的转动惯量改变量;，为由挠性附件(帆板)转动引发的转动惯量附加项;ΔⅠi=ΔⅠic+ΔⅠiu+ΔⅠcu，为由挠性变形和整星质心浮动引起的附加项Ⅰi的改变量，其中ΔⅠic=，为挠性附件振动运动引起的整星角动量改变量;E3为3×3单位阵;Mi为第i个挠性附件的质量为第i个挠性附件未变形前的质心相对于连结点的位置矢量;在式(8)的整个推导过程中没有忽略项.

由动量矩定理，对式(8)两边求导，并假设ω，ωi和uik为一阶小量，经过推导并化简可得

其中Ⅰi为挠性附件i的转动惯量，且

式(9)即为基于质心浮动模型推导得出的卫星姿态动力学方程，其中gc为与传统模型相比，考虑质心浮动问题的新增项.对于大型航天器，其挠性附件的质量、尺寸都较大，若选用的附件挠性也较大，则会产生较大的质心浮动项，因此使得扰动项gc较大.对于高精度的航天任务，采用此动力学模型能够更加精确地描述大挠性航天器的运动状态.

3 挠性附件的动力学模型

下面用变分原理推导挠性附件的动力学方程.第i个挠性附件的动能为

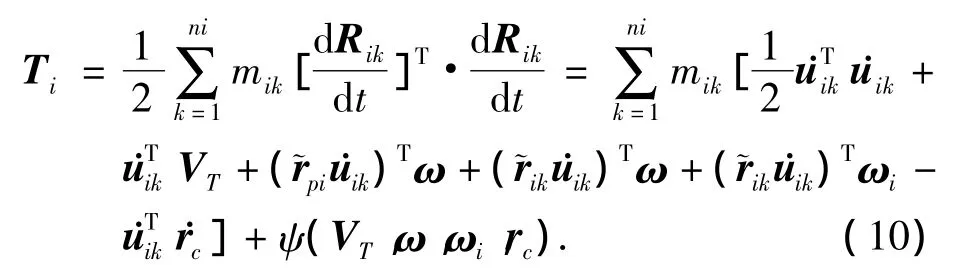
其中ψ(VT，ω)表示只含有VT和ω的项.利用有限元分析结果将式(10)化简可得

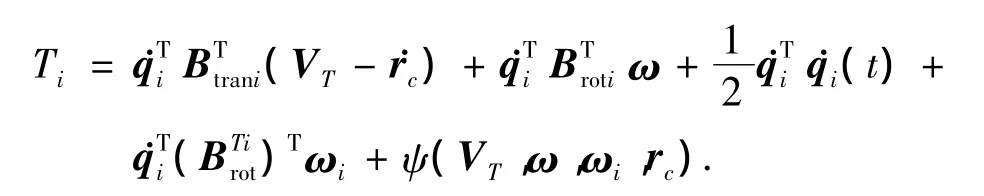
其中qi为第i个挠性附件的模态坐标，Btrani、Broti分别为由有限元分析结果给出的第i个挠性附件的平动、转动耦合系数［14］.

第i个挠性附件的应变势能为

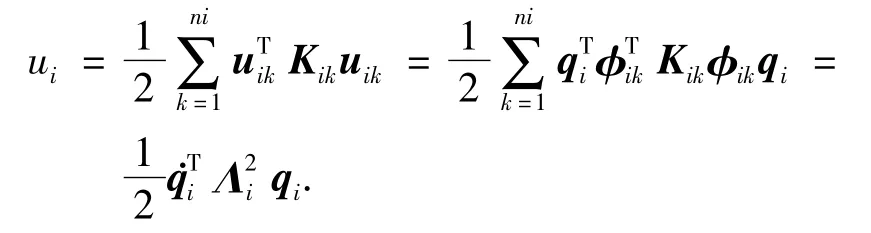
其中Kik是第k个节点的3×3刚度矩阵，Λ2i为N×N对角阵，且

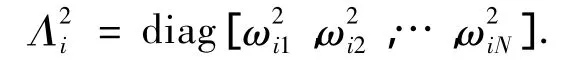
其中ωiN为第i个挠性附件的第N阶模态主频率.

由挠性附件的拉格朗日函数

结合L的变分方程

可得挠性附件的运动方程为

若考虑挠性附件的结构阻尼ζ，则式(11)可写成

将式(9)、(12)联立，即为本文所给出的建立在浮动质心上的带挠性附件的航天器姿态动力学方程组:

将式(13)给出的模型与文献［14］中的动力学模型相比较可知，本文给出的动力学模型包含了系统质心相对于航天器结构的运动状态，可以直接量化给出由附件挠性振动引起的系统质心变化量，继而可得出挠性振动对航天器整体的动力学特性(如系统转动惯量等)的影响，同时还可用于分析挠性附件振动对卫星轨道、姿态运动状态的影响.此外，该动力学模型中包含了挠性附件的运动学项ωi，还可用于分析挠性附件(太阳帆板、机械臂等)的相对运动对航天器整体的影响.

应指出，虽然本文的动力学模型在推导过程中假设飞行器由一个中心刚体B和m个一端与其相连的挠性附件组成，但并不意味着该模型仅局限于此情况适用:当飞行器不包含挠性附件时，可令m=0，此时该动力学模型将退化为刚体动力学模型;当飞行器包含多个刚体时，可将其所有刚性部分视为一个刚性主体进行等效.综上，本文所建立的动力学模型对于不同的航天器普遍适用.

4 仿真算例分析

本节应用前述章节所建立的模型，对带挠性附件的卫星姿态机动过程进行仿真，通过对仿真结果的分析，说明本文所建立的模型的优点.

本算例中，采用的挠性卫星模型为单刚体主体结构与单挠性附件组合的模式，以尽可能突出本文提出的浮动质心模型对飞行器实际姿轨状态的真实反映程度，主体和附件动力学参数的选取参照某实验飞行器配置指标给出，具体参数如下:

挠性卫星的转动惯量矩阵和耦合矩阵分别为

振动频率矩阵为

Λ=diag(0.9513 5.5078 5.7617 6.8594 14.8189)(rad/s).

阻尼矩阵为

ζ=diag(0.005 0.006 0.007 0.008 0.009).

执行机构采用控制力矩陀螺装置，控制律选用PD控制，卫星的初始姿态角θ=［3015-30］T，初始姿态角速率=［0 0 0］.卫星从t=0开始进行姿态机动，最后稳定在目标姿态.仿真结果如图2～5所示.

图2 卫星姿态角、姿态角速度变化

图3 挠性附件各阶模态变化历程

图2为卫星的姿态角和角速度在机动过程中的变化历程，从中可看出卫星在控制律作用下姿态机动至指定姿态且达到稳定，姿态指向精度可达 0.05°，姿态稳定度优于 0.01(°)/s，说明经典的PID控制律能够与浮动质心模型相适应，且控制效果可以达到较高水平.

图3为在卫星姿态运动过程中挠性附件的振动模态变化历程，从中可以看出，在整个姿态机动过程中，挠性附件始终存在一定幅度的挠性振动，其振动幅度趋于收敛.

图4为由附件的挠性振动引发的卫星质心浮动情况，从中可以看出，对于带有挠性附件的卫星，其在姿态运动过程中激发的挠性附件的振动会引起整星质心的周期性浮动，在本算例中，质心浮动位移幅值接近厘米级，质心浮动速度幅值为毫米/秒级.

图4 质心浮动位移、速度变化历程

图5为质心浮动引起的扰动力矩，即式(9)中的gc项，从图中结果可以看出，在整个姿态机动过程中，由卫星的质心浮动引起的扰动力矩幅值的量级为10-2N·m级，在通常情况下，在轨卫星受到的环境扰动力矩(如重力梯度力矩、光压力矩、地磁力矩等)的量级均在10-3N·m以下，由此可见该扰动力矩对航天器的姿态会有较为显著的影响.将此仿真计算结果与国内某科研院所的在轨实验数据相比较，结果具有一致性，由此可知该动力学模型在实际工程应用中也具有适用性.

图5 质心浮动带来的扰动力矩

从仿真结果可以看出，本文给出的动力学模型能够准确地估计挠性附件振动对在轨卫星质心的浮动影响，并可以计算出质心浮动对卫星整体姿态的干扰力矩，对提高姿态控制精度具有重要意义.此外，该动力学模型还可用于计算由这种质心浮动引起的各动力学要素的改变量，如整星转动惯量改变量、执行机构偏差量等，并由此结合卫星具体任务的精度指标需求，对导航、测量等系统的精度提出要求.该仿真结果与某科研院所给出的实验数据较为相符，符合工程约束，具有较好的实践性.

5 结语

针对挠性航天器动力学问题，提出了一种建立在浮动质心上的动力学模型，该模型更符合航天器在轨飞行过程中挠性附件运动与航天器本体姿态、轨道的动力学耦合实际情况.应用此模型能准确计算由附件挠性振动引起的航天器质心相对于其结构的浮动位移与速度，进而可计算得到质心浮动引起的航天器动力学特性的改变.在工程上应用该模型，能够减小模型误差，提高控制精度，同时可根据此模型的计算结果，对测量、执行机构的性能指标提出要求，以满足当前工程任务中日益提升的精度需求.

［1］ JIA Q，YAO W，CHEN G，et al.The trajectory tracking ofspace flexible manipulatorwith large payloads based on optimal control［C］//The8 th IEEE Conference on Industrial Electronics and Applications(ICIEA 2013).Melbourne:IEEE Industrial Electronics，2013:1569-1573.

［2］DATASHVILI L，ENDLER S，WEI B，et al.Study of mechanical architectures of large deployable space antenna apertures:from design to tests［J］.CEAS Space Journal，2013，5(3/4):169-184.

［3］BORGGRAFE A，HEILIGERS J，CERIOTTI M，et al.Distributed reflectivity solar sails for extended mission applications［C］//3rd International Symposium on Solar Sailing.Glasgow:Springer Berlin Heidelberg，2014:331-350.

［4］ JOHNSON T L.Progress in modelling and control of flexible spacecraft［J］.Journalofthe Franklin Institute，1983，315(5):495-520.

［5］缪炳祺，曲广吉.关于柔性航天器的动力学建模问题［J］.航天器工程，1998，7(3):26-32.

［6］岳宝增，宋晓娟.具有刚-柔-液-控耦合的航天器动力学研究进展［J］.力学进展，2013，43(1):162-172.

［7］POSHBERGH T A.Modeling and control of mixed and flexiblestructures， ADA444248［R］. Maryland:Maryland Univ College ParkSystems Research Center，1988.

［8］WANG Y，HUSTON R L.A lumped parameter method in the nonlinear analysis of flexible multibody systems［J］.Computers＆ Structures，1994，50(3):421-432.

［9］KAMESH D，PANDIYAN R，GHOSAL A.Modeling，design and analysis of low frequency platform for attenuating micro-vibration in spacecraft［J］.Journal of Sound and Vibration，2010，329(17):3431-3450.

［10］NGUYEN P K，HUGHES P C.Finite-element analysis ofCTS-like flexible spacecraft［M］. Toronto:University of Toronto，1976.

［11］贾英宏，徐世杰.带弹性附件的航天器的动力学与变结构控制［J］.哈尔滨工业大学学报，2003，35(1):1-4.

［12］蒋建平，李东旭.带太阳帆板航天器刚柔耦合动力学研究［J］.航空学报，2006，27(3):418-422.

［13］崔乃刚，刘家夫，荣思远.柔性太阳帆航天器动力学建模与姿态控制［J］.哈尔滨工业大学学报，2011，43(7):1-5.

［14］屠善澄.卫星姿态动力学与控制(4)［M］.北京:中国宇航出版社，2006:420-424.