ODA-IPNMF:一种在线全网络流量异常检测方法
柏 骏,夏靖波1,吴吉祥3,鹿传国4
(1.空军工程大学信息与导航学院,710077西安;2.95852部队,572600海南东方;3.空军大连通信士官学校,116600辽宁大连;4.95806部队,100076北京)
ODA-IPNMF:一种在线全网络流量异常检测方法
柏 骏1,2,夏靖波1,吴吉祥3,鹿传国4
(1.空军工程大学信息与导航学院,710077西安;2.95852部队,572600海南东方;3.空军大连通信士官学校,116600辽宁大连;4.95806部队,100076北京)
为实时、高效地检测网络流量异常,提出一种基于增量投影非负矩阵分解(IPNMF)的全网络流量异常检测方法(ODA-IPNMF).提出一种增量投影非负矩阵算法,该算法不仅具有与PCA相同的表达形式,还能以增量的方式构建正常子空间和异常子空间,进而利用Shewhart控制图实现全网络流量异常的在线检测.理论分析表明,该方法计算开销远小于NMF-NAD,具有更高的实用价值;模拟网络数据以及实测网络数据实验表明,基于NMF异常检测方法(NMF-NAD和ODAIPNMF)的检测性能优于PCA方法;本文所提ODA-IPNMF与NMF-NAD网络异常检测效果相当,且可在线检测网络异常.
网络异常检测;流量矩阵;增量投影非负矩阵分解;在线检测
随着互联网技术的迅猛发展,各类网络异常活动如影随形,网络安全成为各方关注的焦点.异常检测对于维护网络安全、高效、可靠运行具有重要意义,是网络安全领域的研究热点[1-9].
从全网的视角实时检测网络异常对于维护网络稳定运行极为重要.文献[3-4]提出基于流量矩阵子空间映射的全网络异常检测方法,该方法利用流量矩阵的空间相关性和时间相关性,从全网络的视角检测异常行为.文献[5]指出基于PCA异常检测方法对于主成分数量、检测阈值等参数的选取非常敏感,而且连续的或者足够大的网络异常可能毒害正常子空间,并致使误报率增加.文献[6]利用奇异值分解(SVD)实现PCA的在线更新,进而实现全网络的多元在线异常检测.文献[7]先利用小波去除数据中的噪声,以减轻大的异常对于正常子空间的毒害,再使用PCA将流量矩阵映射到正常和异常子空间.文献[8]亦做了类似的工作,将PCA和小波分析结合起来以提高流量异常检测的精度.针对基于PCA的异常检测方法难以解释矩阵分解过程中出现的负值以及无法连续检测异常的问题,文献[9]提出利用非负矩阵分解检测网络异常,将原始流量矩阵与重构矩阵的差视为噪声和异常,并通过Shewhart控制图捕捉网络异常,但该文献并未对方法的合理性做出解释,并且只能离线检测网络异常.
本文采用与PCA表达形式相同的投影非负矩阵分解算法(PNMF)作为检测工具,提出了一种基于IPNMF的在线全网络流量异常检测方法(ODA-IPNMF).将PNMF引入到基于流量矩阵的全网络异常检测中,并提出了一种增量投影矩阵分解算法——IPNMF;提出一种基于IPNMF的全网络异常检测方法,该方法以增量的方式对流量矩阵进行投影,构建正常子空间和异常子空间,可实时检测网络异常.
1 流量矩阵及PNMF算法
1.1 流量矩阵
流量矩阵TM(traffic matrix)是全网络流量概览,可全面、准确地描述网络流量特征(流量大小、字节数、IP地址、端口等)的分布情况[10].矩阵中的元素代表网络中某一时刻(时间间隔)源节点与目的节点之间(OD对)的流量,可表示为一个d×p的矩阵X.其中,d为测量的周期数;p为n个网络节点的OD对数,有p=n×n(或p=n× (n-1)).Xij为在第i个测量周期时第j个OD对的流量特征数据的测量值.根据选择的网络节点类型不同,可以分为链路级、路由级和PoP(point of presence)级流量矩阵.本文以PoP级流量矩阵作为研究对象.
1.2 PNMF算法
为应对高维数据“维度诅咒”问题,多采用矩阵分解来分析实际问题中的高维数据,如PCA、ICA、SVD、VQ等.然而上述方法分解的矩阵元素可能出现负数往往无法得到合理的解释,因此,文献[11]的非负矩阵分解应运而生.
对任意给定的非负矩阵X∈Rd×p+进行分解,试图寻找最优解W和H使得

并通过迭代使得二者之间的近似误差最小,用欧式距离衡量,有

PNMF[12]是一个改进的NMF算法,它试图寻找一个非负的投影矩阵使得
式中的投影矩阵可进一步表示为


PNMF算法为求得最佳W,定义了如下优化问题:

对X求偏导,有
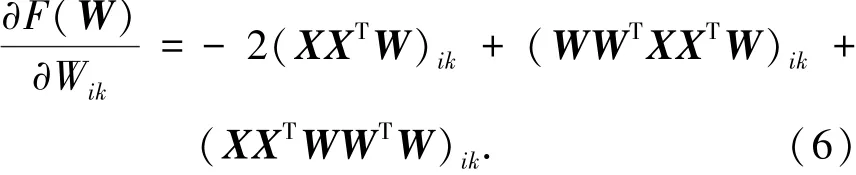
令

带入上式,得到

进而得到更新方程:
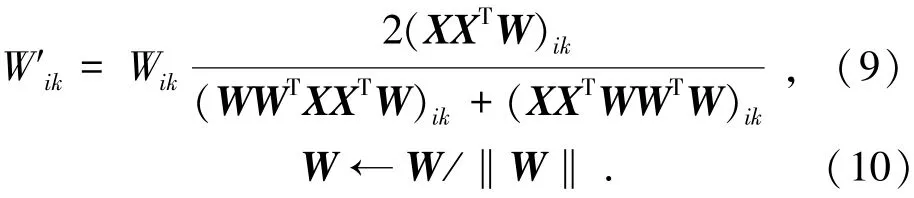
较其他NMF算法,PNMF更适用于流量矩阵的网络异常在线检测.首先,PNMF与与基于PCA的异常检测算法[3]具有相同的表达形式,可将流量矩阵向正常子空间和异常子空间上进行投影;其次,通过PNMF不仅可得到非负的稀疏矩阵,而且只需考虑更少的参数,就能产生更稀疏的矩阵,便于在线流量异常检测;而且,PNMF在不断迭代的过程中,可将正常与异常子空间的差异最大化,具备更佳的检测效果.
2 ODA-IPNMF算法
采用子空间分析方法[3]检测流量异常的前提是分离正常子空间和异常子空间,并对异常子空间进行分析以检测网络是否出现异常.上述PNMF算法只能对流量矩阵进行离线的批量处理,无法以增量的方式分离正常、异常子空间.因此,为克服PNMF只能进行离线数据处理的不足,提出一种增量投影非负矩阵分解算法(IPNMF).
增量计算是一个不断利用前面处理结果进行后续增量运算的过程.那么增量过程的关键就是如何利用已得到的计算结果.文献[13]指出,增量非负矩阵分解过程中,基向量代表了之前数据的所有信息.基于此,将新增样本数据D(t)添加到上一时刻的基向量W(t-1)中作为IPNMF算法的新的输入向量X(t),记为X(t)=[W(t-1),D(t)];然后将X(t)代入式(9)和式(10)中,不断迭代直至收敛.在迭代过程中,主要的计算是式(9)中的矩阵乘法,为减少运算量,令

下面给出IPNMF算法的伪代码:

基于以上分析,本文采用子空间分析方法,利用IPNMF将流量矩阵映射到正常子空间和异常子空间中,然后利用Shewhart控制图捕捉异常子空间中的流量异常.该方法步骤如下:

3)异常流量捕获.为了对残余矩阵进行分析,本文引入残余流量向量中所有元素的平方和(SSE)来衡量残余向量的大小,并利用Shewhart控制图来捕捉异常子空间中的流量异常.
利用上述的IPNMF增量算法思想实现全网络流量异常的在线检测——ODA-IPNMF,算法描述如下:

ODA-IPNMF方法的计算开销主要在于增量数据D(t)的IPNMF分解和基于Shewhart的异常检测.增量数据D(t)的IPNMF的时间复杂性为O(pr(r+s)k),其中p为OD对数,r是基矩阵维数,s为增量数据维数,k为迭代次数.而基于Shewhart的异常检测的时间复杂性仅与增量数据维数s相关,为O(s),远小于前者.因此,ODAIPNMF方法的时间复杂性为O(pr(r+s)k),相比于文献[9]的O(pdrk),其中(r+s)≪d,那么所提方法的运算效率有明显提高.
3 实验分析及评价
为对所提ODA-IPNMF算法性能进行分析、评价,本文基于Matlab实验平台,以检测率和误检率作为评价指标,采用模拟实验分析与因特网实测数据分析相结合的方式来比较异常检测算法的检测性能.
3.1 模拟数据实验及其分析
3.1.1 模拟数据生成
首先产生近似周期性的正常成分、高斯噪声成分和异常成分[14],再按适当的比例人工合成网络流量.具体步骤:1)通过将3种不同周期、随机初始相位的正弦波叠加来模拟OD流,进而构成基准流量矩阵,图1(a);2)在OD流上加入零均值的高斯噪声,得到不含异常的基准流量矩阵,见图1(b);3)以一定规则注入各类典型异常,见图1(c).采用间隔为5 min,共模拟一个星期的网络流量,最终生成包含2 016个测量周期、121条网络流的流量矩阵X.
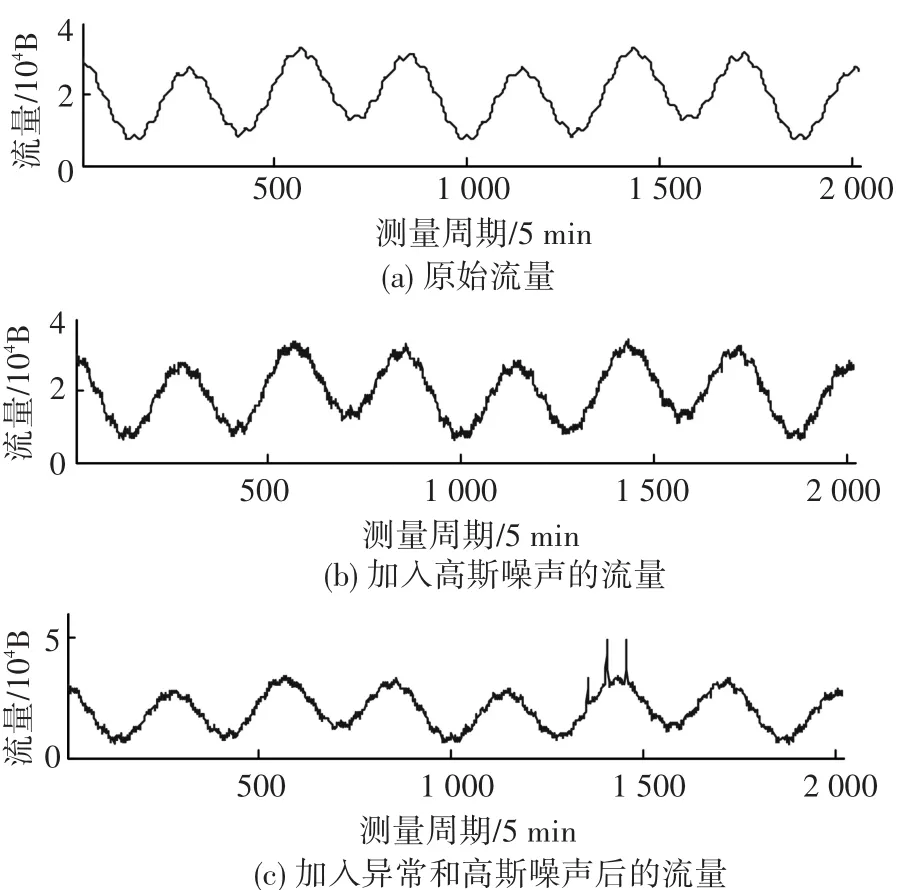
图1 模拟网络流量数据合成
本文所提方法是从流量大小的角度去检测异常,故在此考虑4种最常见的、引起流量剧烈变化的典型异常:阿尔法(alpha)异常、(分布式)拒绝服务攻击(DoS,DDoS)、突发流(flash crowd)、入口/出口移动(ingress/egress shift)异常,并利用持续时间、流量变化大小、源-目的数以及形状函数等4个参数来描述.上述异常的具体行为特征参见文献[6].
网络异常注入过程如下:从第250个测量周期到第500个测量周期,每50个测量周期注入一次持续30 min(6个测量周期)阿尔法攻击;从第750个测量周期到第1 000个测量周期,每50个测量周期注入一次持续时间为30 min(6个测量周期)DDoS攻击;从第1 250测量周期到1 500测量周期,每50个测量周期注入一次突发流;在第1 900测量周期到1 950测量周期内注入一次入口/出口移动异常.
3.1.2 IPNMF算法性能分析及参数选取

为比较本文所提IPNMF算法与PNMF算法的收敛性以及矩阵还原性,在固定基矩阵维数r= 3的条件下,利用上述两种算法对模拟实验数据重复10次,得到的实验结果见表1.

表1 IPNMF算法与PNMF算法性能比较结果
从表1中看出IPNMF算法对收敛性的明显改善,矩阵分解过程中的迭代次数以及收敛时间都大幅减少.一方面原因是IPNMF算法的时间复杂性低于PNMF算法;另一方面则是IPNMF算法所需存储的最大矩阵规模为m×(r+s),远小于后者的m×(n+s),节省了大量存储资源.此外,两种投影非负矩阵分解算法的d值相差无几,因此二者具有相当的矩阵还原性.
非负矩阵分解算法的一个非常重要的参数是基矩阵维数r.为确定基矩阵维数,本文设置最大迭代次数为500,另r从2递增至20,以寻求最优的矩阵还原性.实验重复10次,实验结果见图2.

图2 基矩阵维数r与算法性能的关系
3.1.3 ODA-IPNMF算法性能分析与比较
将本文所提ODA-IPNMF与MOADA-SVD方法[6]和NMF-NAD方法[9]进行比较.MOADA-SVD是基于奇异值分解的在线网络异常检测方法,采用Q统计量的方法检测异常;NMF-NAD是基于NMF的离线网络异常检测方法,采用Shewhart控制图的方法进行异常检测.上述3种算法异常时刻凸显的结果见图3.

图3 3种方法的异常凸显对比
由图3可发现,相较于MOADA-SVD方法,基于NMF的异常检测方法(NMF-NAD和ODAIPNMF)对网络异常更为敏感,其异常/正常流量的幅值比明显大于前者,更易被检测,且误检率更低.究其原因,MOADA-SVD仍是基于PCA算法,它力求寻找均方误差最小意义下的最优线性映射投影,却忽略了正常流量与异常流量的属性差异,导致可能包含的重要信息丢失;而NMF在不断迭代的过程中将这种差异最大化,因而具有更佳的异常检测效果.
在图4中,利用Shewhart对ODA-IPNMF与NMF-NAD的检测结果进行比较,其中R为流量变化范围,在[LCL,UCL]区间内即为正常.结合图3(b)和图3(c),可以看出,上述两种方法对全网络异常的凸显几乎是一样的,唯一不同在于第1 900到1 950测量周期的入口/出口移动异常检测结果,NMF-NAD方法表现出连续异常,而本文算法表现为突发异常.究其原因,本文方法采用增量分解算法,以6个测量周期进行矩阵分解,残余矩阵中的连续流量信息容易被忽略,导致连续异常未能被充分检测.此外,ODA-IPNMF算法以增量的方式实时检测网络异常,每次需处理的数据仅与时间间隔t有关,数据量远远小于一次性分解全流量矩阵,所占用的存储空间以及计算资源要远远小于NMF-NAD算法,因而实际应用价值更高.
重复上述实验过程10次,3种算法的检测结果见表2.通过比较发现,NMF-NAD和 ODAIPNMF方法无论是检测率还是误检率都相差无几,且明显优于 MOADA-SVD方法,而后者与文献[3]的结果吻合.实验表明,NMF具备更优异的异常检测能力.
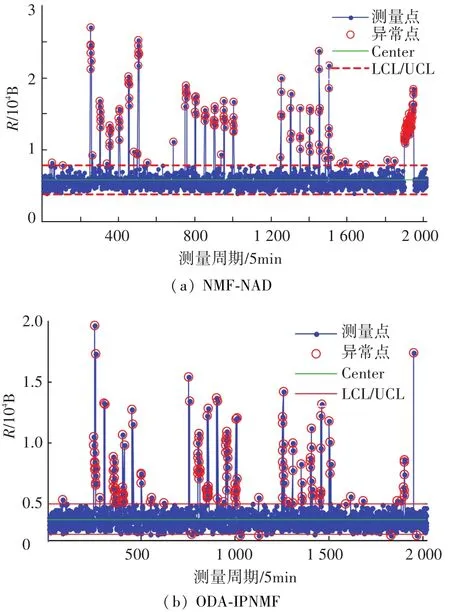
图4 基于Shewchart的异常检测结果
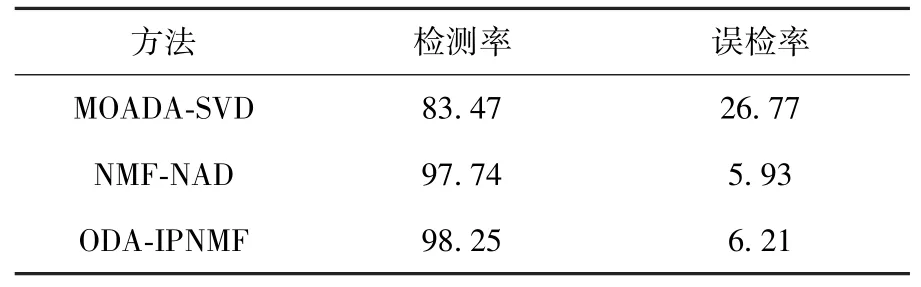
表2 异常检测结果 %
3.2 实测数据实验及其分析
3.2.1 实测数据集Abilene
为验证、评价上述方法在实际网络中异常检测的效果及性能,本文采用来自于Abilene网络的流量矩阵数据,其描述如表3所示.上述数据集自身便含有网络异常,发现并确定异常是检测的关键.
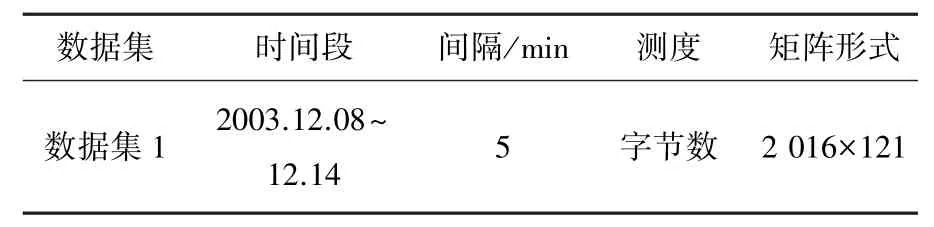
表3 Abilene流量矩阵
3.2.2 ODA-IPNMF算法实验分析
按照上述实验流程对Abilene流量矩阵数据进行异常检测.其中Dataset1的3种方法的异常凸显结果见图5.
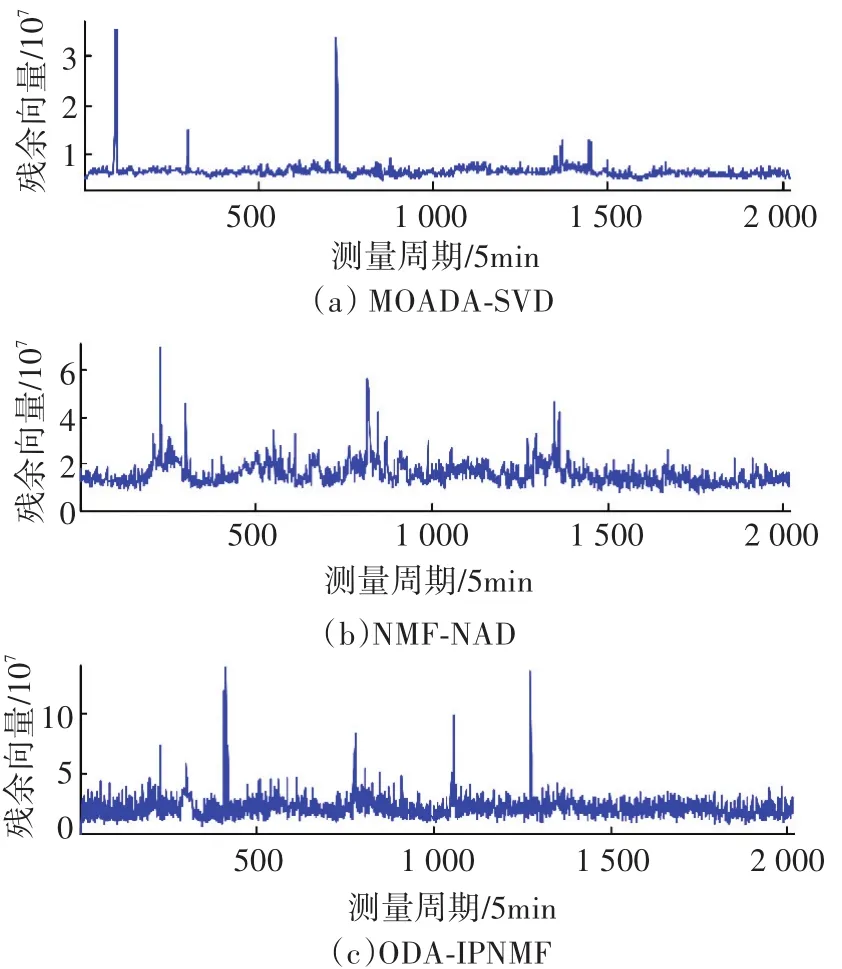
图5 Dataset1数据集异常凸显结果
实测网络数据的异常检测结果很好地验证了模拟数据的实验结论.MOADA-SVD方法仅发现了3处网络异常,而其他两种方法则发现了包括上述异常在内的5至6处异常,表明基于NMF的异常检测方法(NMF-NAD和ODA-IPNMF)在异常检测性能上优于基于PCA的检测方法;本文提出的基于增量NMF的在线异常检测算法ODA-IPNMF与NMF-NAD相比,在异常检测性能上是相当的,但对于不同的异常表现出一些差异.
4 结 语
实验与分析表明基于NMF的异常子空间投影方法较基于PCA的方法更利于网络流量矩阵异常检测.然而现有基于NMF的异常检测方法只能处理离线数据,无法对网络流量进行在线检测.针对这一不足,本文给出了一种增量非负矩阵分解算法,并将其应用于网络异常检测中,并利用Shewart控制图分析残余流量,提出了一种基于IPNMF的在线全网络流量异常检测方法.该方法以增量的方式实时检测网络异常,所占用的存储空间以及计算资源要远远小于NMF-NAD算法.通过模拟数据以及实测网络数据实验表明本文所提方法具备良好的全网络异常流量检测效果.
[1]BHUYAN M H,BHATTACHARYYA D K,KALITA J K.Network anomaly detection:methods,systems and tools[J].Communications Surveys&Tutorials,IEEE,2014,16(1):303-336.
[2]HUANG S Y,HUANG Y N.Network traffic anomaly detection based on growing hierarchical SOM[C]//2013 43rd Annual IEEE/IFIP International Conference on Dependable Systems and Networks(DSN).Budapest: [s.n.],2013:1-2.
[3]LAKHINA A,CROVELLA M,DIOT C.Diagnosing network-wide traffic anomalies[C]//ACM SIGCOMM Computer Communication Review,[S.l.]:ACM,2004,34(4):219-230.
[4]LAKHINA A,CROVELLA M,DIOT C.Mining anomalies using traffic feature distributions[C]//ACM SIGCOMM Computer Communication Review,[S.l.]: ACM,2005,35(4):217-228.
[5]RINGBERG H,SOULE A,REXFORD J,et al.Sensitivity of PCA for traffic anomaly detection[C]// ACM SIGMETRICS Performance Evaluation Review,[S.l.]:ACM,2007,35(1):109-120.
[6]钱叶魁,陈鸣.基于奇异值分解更新的多元在线异常检测方法[J].电子与信息学报,2010,32(10): 2404-2409.
[7]钱叶魁,陈鸣,叶立新,等.基于多尺度主成分分析的全网络异常检测方法[J].软件学报,2012,23 (2):361-377.
[8]NOVAKOV S,LUNG C H,LAMBADARIS I,et al.Studies in applying PCA and wavelet algorithms for network traffic anomaly detection [C]//High Performance Switching and Routing(HPSR),2013 IEEE 14th International Conference on,[S.l.]:IEEE,2013:185-190.
[9]魏祥麟,陈鸣,张国敏.NMF-NAD:基于NMF的全网络流量异常检测方法[J].通信学报,2012,33 (4):54-61.
[10]VARDI Y M.Network tomography:estimating sourcedestination traffic intensities from link data[J].Journal of theAmerican StatisticalAssociation, 1996, 91 (433):365-377.
[11]LEE D D,SEUNG H S.Learning the parts of objects by non-negative matrix factorization[J].Nature,1999,401:788-791.
[12]YANG Z,OJA E.Linear and nonlinear projective nonnegative matrix factorization[J].IEEE Transaction on Neural Networks,2010,21(5):734-749.
[13]DONOHO D,STODEEN V.When does non-negative matrix factorization give a correct decomposition into parts? [C]//Advances in Neural Information Processing Systems,2004:1141-1148.
[14]LAKHINA A,PAPAGIANNAKI K,CROVELLA M,et al.Structural analysis of network traffic flows[C]// SIGMETRICS,New York,NY,USA:[s.n.],2004: 156-167.
(编辑 苗秀芝)
ODA-IPNMF:An Online Anomaly Detection Algorithm
BAI Jun1,2,XIA Jingbo1,WU Jixiang3,LU Chuanguo4
(1.Institute of Information and Navigation,AFEU,710077 Xi'an,Shanxi,China;2.Unit 95852,572600,Dongfang,Hainan,China;3.Air Force Dalian Communications Noncommissioned Officers School,116600,Dalian,Liaoning,China;4.Unit 95806,100076 Beijing,China)
An online anomaly detection algorithm based on incremental projective non-negative matrix factorization is proposed to detect the network anomaly real-timely and efficiently.Firstly,an incremental projective non-negative matrix factorization is given,which has the same expression with PCA,and is able to construct normal and abnormal subspace to detect network-wide anomalies online by Shewhart control chart.Theoretic analysis indicates that,the proposed algorithm computation is far smaller than NMF-NAD.In addition,traffic matrix datasets analyzing for internet and simulation results show that the network anomalies detection algorithms based on NMF(such as NMF-NAD and ODA-IPNMF)performs better than that based on PCA,and the proposed ODA-IPNMF has comparable network anomaly detection by NMF-NAD,which the ability to detect the network anomaly online.
network anomalies detection; traffic matrix; incrementalprojective non-negative matrix factorization;online detection
TP393
A
0367-6234(2015)05-0104-06
10.11918/j.issn.0367-6234.2015.05.018
2014-06-19.
国家自然科学基金(61272486);陕西省科技计划自然基金重点项目(2012JZ8005).
柏 骏(1985—),男,博士研究生;
夏靖波(1963—),男,教授,博士生导师.
柏 骏,peking1985-2005@163.com.

