微波加热用磁控管电源的设计
陈家新, 汤 勇, 沈 勇, 王珍珍, 胡 成
(东华大学 信息科学与技术学院, 上海 201620)
微波加热与传统的加热相比,具有加热均匀、速度快、热利用效率高等优点,所以微波加热技术在各个领域也得到越来越广泛的应用。 用于产生微波的磁控管是微波加热器的核心元件,它可以将直流电能转换为微波能,所以说设计微波加热电源的关键实质上就是给磁控管提供电源[1-2],一般为4 000 V 左右的高压直流电。 目前中国市场上的大部分磁控管供电电源都是采用工频变压器升压后半波倍压整流的工作方式, 但是这样的设计方案带来的问题是电源的效率低、体积大、重量重,磁控管的使用寿命大大降低,所以设计一款效率高、体积小、重量轻的微波加热用磁控管电源就显得意义非常重大。
近些年来,谐振变换器由于其效率高、EMI 小、能实现软开关等一系列优点得到越来越多的关注和研究。 LLC 谐振变换器由于兼具串联谐振变换器和并联谐振变换器的优点,也得到更多国内外研究学者的重视和青睐,对这一拓扑结构的理论研究和分析也更加深入。 但是这些研究内容都局限于低电压、小功率的应用场合,没有牵涉到输出几千伏的高电压、上千瓦的大功率的应用领域。所以本文提出将LLC 谐振变换器用于高电压、大功率的应用场合,利用半桥LLC 谐振变换器作为主拓扑结构,设计一款微波加热用磁控管供电电源[3-4]。为了提高输出电压,输出端采用倍压整流电路,给负载磁控管的阳极提供高压直流电。采用这种LLC 谐振变换器和倍压整流相结合的工作方式, 会使得磁控管供电电源效率高、输出电压稳定,大大提高磁控管的使用寿命[5]。
目前市面上的仿真软件特别多, 而且功能都很强大,其中,SABER 具有更加丰富的元件库和更加精确的分析能力,仿真效果逼真直观, 所以SABER 在电源仿真领域有着非常广泛的应用[6-7]。文中在给出半桥LLC 谐振变换器主电路的参数设计后,利用SABER 软件进行仿真,给出仿真结果,对理论分析进行验证。
1 主电路原理图与工作原理
1.1 主电路原理图
磁控管供电电源的主电路原理图如图1 所示,采用半桥LLC 谐振变换器作为主电路拓扑结构,输出端采用倍压整流的方式给磁控管阳极供电。 其中,Ug为交流输入市电,D1、D2、D3、D4、L 和C 组 成 整 流 滤 波 电 路,VD1 和VD2 分 别 是Q1 和Q2 的体二极管。 Ug1和Ug2是固定0.5 占空比且带有死区时间的触发脉冲, 由单片机产生, 分别驱动开关管Q1 和Q2,能有效防止上下两个管子直通。Q1 和Q2 的寄生电容、缓冲电容和各种杂散电容之和等效为C0,Cr是串联谐振电容,Lr是 变 压 器 的 漏 感,Lm是 变 压 器 的 励 磁 电 感,Cr、Lr和Lm组 成LLC 谐振电路。 T 为高频变压器,N2 为高压绕组,N3 为灯丝绕组。 VD3、VD4、C3 和C4 组成倍压整流滤波电路为负载磁控管M 的阳极提供高压直流电。
1.2 LLC 谐振变换器工作原理
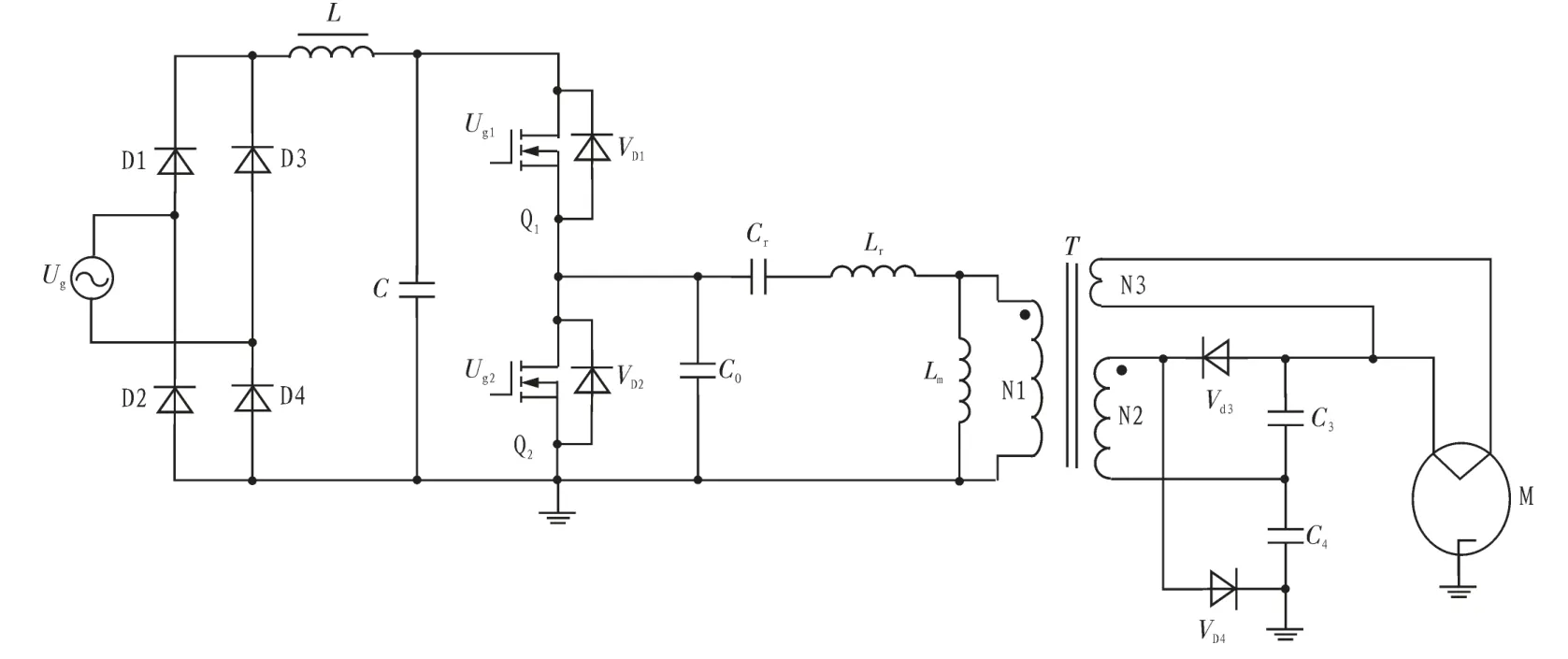
图1 磁控管供电电源主电路原理图Fig. 1 The principle diagram of the magnetron power supply main circuit
LLC 谐振变换器电路有两个谐振频率,一个是谐振电感Lr和谐振电容Cr谐振产生的串联谐振频率fr,另一个是励磁电感Lm加上串联谐振电感Lr与谐振电容Cr谐振产生的串并联谐振频率fm。 其中,

开关管的工作频率为fs, 在实际设计时通常让开关管的工作频率在fm<fs≤fr的范围内,这样可以很方便地实现开关管的零电压开通,从而实现软开关[8]。 磁控管供电电源主电路的主要波形如图2 所示, 从图中可以看出,Q1 和Q2 互补导通且留有死区时间,谐振电容Cr的电压波形和串联谐振电感Lr的电流波形都呈正弦规律变化。

图2 LLC 谐振变换器主电路的主要波形Fig. 2 The main waveform of the LLC resonant converter main circuit
1.3 变压器偏磁饱和解决方法
变压器偏磁是半桥变换器中存在的一个普遍现象,并且偏磁导致的后果非常严重。 目前的文献中提出的方法和措施都只能缓解变压器偏磁,但是不能从根本上解决问题,这里给出一种新颖的能够从根本上解决变压器偏磁饱和问题的方法。
在EE 型变压器的两侧中间各开一个很小的气隙, 各插入一个单极性霍尔传感器开关,霍尔传感器的输出接到单片机进行采样,实时检测变压器的磁感应强度B 的大小。 当单片机检测到由高到低变化的电平时,说明磁感应强度B 已增加到饱和值, 此时把该电平翻转信号传递给单片机的FLT0引脚,关闭半桥变换器的Ug1和Ug2脉冲,从而实现了从根本上有效解决变压器的偏磁饱和问题。 此方法简单有效,成本较低,可靠性较好。
2 半桥LLC 谐振变换器的建模
为了便于分析,将半桥LLC 谐振变换器主电路原理图进行分解,划分成开关网络、谐振网络和倍压整流网络3 个部分模型,如图3 所示。 假设开关管的工作频率fs接近于串联谐振频率fr,下面用基波分析法分别对这三部分进行建模分析。
2.1 开关网络
开关网络的输入为Uin, 它是市电经过整流滤波后得到的直流电压。 对开关网络的输出电压Uio(t)进行傅里叶分解,可得
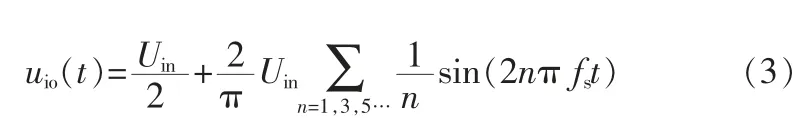
其基波电压为

基波电压分量有效值为

2.2 倍压整流网络
倍压整流网络的输出为磁控管的阳极提供高压直流电,设输出稳定电压为U0, 同样的采用傅里叶分解计算化简后,得倍压整流网络输入电压的基波分量有效值为

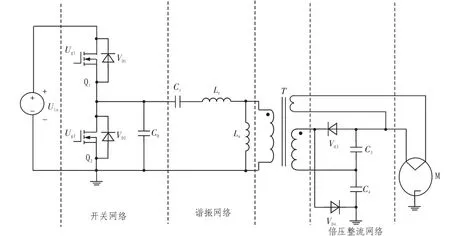
图3 半桥LLC 谐振变换器模型Fig. 3 The model of the half-bridge LLC resonant converter
负载磁控管可以等效为电阻值固定的RL,高频变压器初次级绕组的匝数比为n,将负载RL折算到高频变压器原边的等效电路如图4 所示,其中

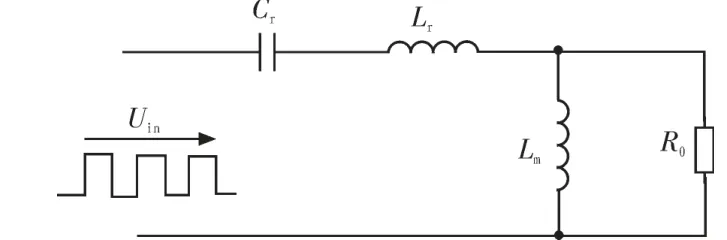
图4 变压器原边等效电路图Fig. 4 The principle diagram of the magnetron power supply main circuit
2.3 谐振网络
谐振网络的输入电压就是开关网络的输出电压,谐振网络的输出电压就是倍压整流网络输入电压的n 倍,所以谐振网络的增益为

由图4 可以看出谐振网络的输入阻抗为
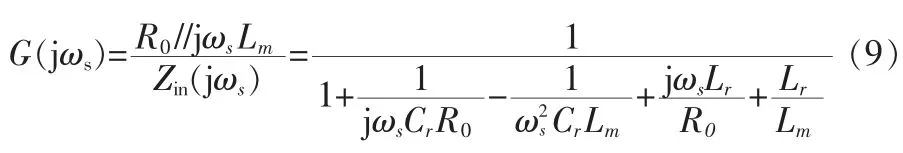
其中,ωs=2π fs。 谐振网络的交流电压增益为
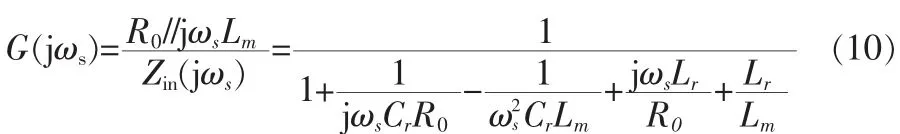
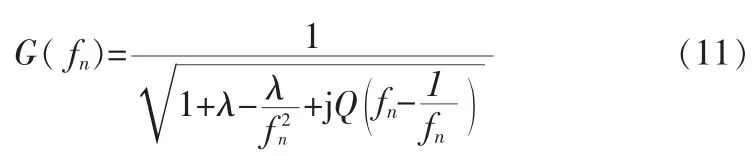
从而可得谐振网络的直流电压增益为

由式(8)和式(12)相等可得LLC 谐振变换器的直流电压增益为
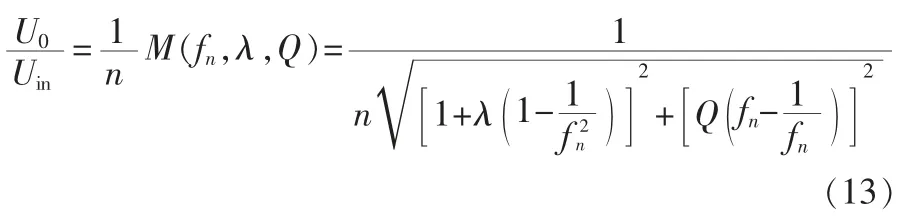
3 主电路参数设计
LLC 谐振变换器工作的核心就是参与谐振的Cr、Lr和Lm,这3 个谐振参数的设计对于整个LLC 谐振变换器的工作效率和工作性能起着至关重要的作用。
3.1 励磁电感Lm 的设计
为了实现变换器的软开关,开关管Q1 和Q2 必须要能够零电压开通, 那么谐振电流必须使得等效电容C0在死区时间Td内完全充电或放电,设变换器的工作效率为η,则励磁电感Lm的设计要满足

3.2 谐振电容Cr 和谐振电感Lr 的设计
电感系数λ 的计算公式为
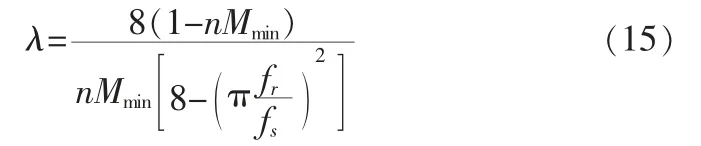
那么,谐振电感Lr为

谐振电容Cr可求出为

至此,LLC 谐振变换器最重要的3 个核心参数都设计出来了,这也是实际设计时必须参考的计算法则。
4 仿真结果
本文以负载磁控管的输出功率1 000 W、阳极电压4 000 V、谐振频率20 kHz 为例,用仿真软件SABER 对所设计的磁控管供电电源主电路进行仿真,得出仿真结果。 经过多次仿真与参数计算修正后,确定谐振参数分别为:Cr=4 μF,Lr=16 μH,Lm=45 μH。死区时间设置为Td=1.5 μs,磁控管M 的等效电阻值算出为16 000 Ω, 主电路SABER 仿真原理图及各元件参数如图5 所示。
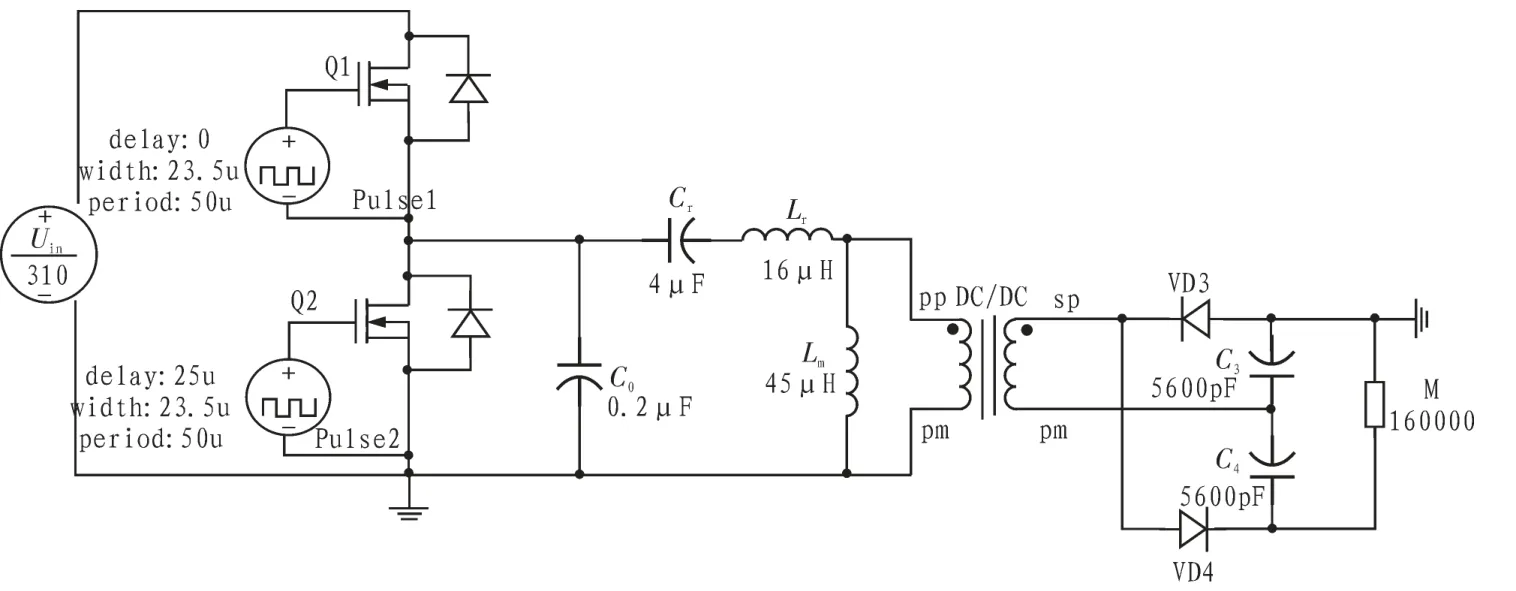
图5 主电路SABER 仿真原理图Fig. 5 The principle diagram of the main circuit SABER simulation
用SABER 软件对所设计的主电路进行仿真, 得到的仿真结果如图6 所示。 图中从上至下的波形依次为:开关管Q1的驱动电压波形、Q1 的漏-源极电压波形、开关管Q2 的驱动电压波形、Q2 的漏-源极电压波形和谐振电容的电压波形。
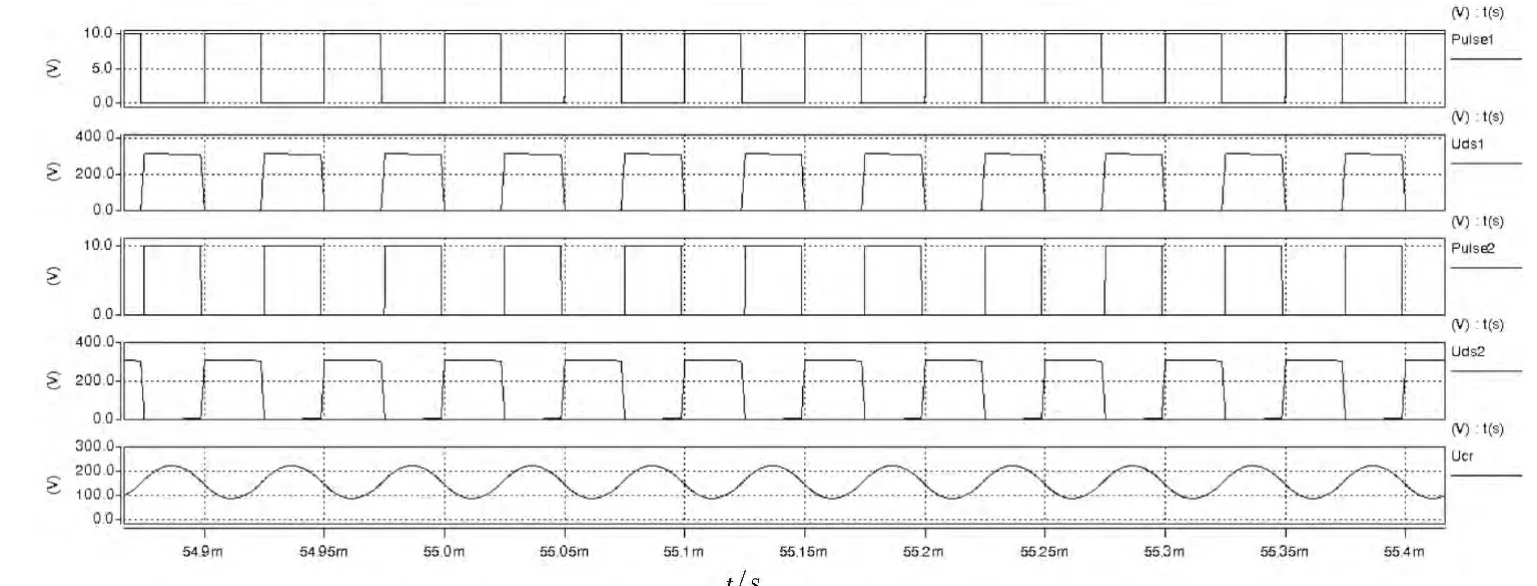
图6 主要仿真波形Fig. 6 The main simulation waveform
从图中可以清楚地看到, 开关管Q1 和Q2 互补导通,占空比为0.5 且留有死区时间,当驱动信号Q1 到来时,开关管Q1 上的电压已经降为零, 所以开关管Q1 实现了零电压开通;当驱动信号Q2 到来时,开关管Q2 上的电压已经降为零,所以开关管Q2 也实现了零电压开通。这样,开关管Q1 和Q2就都实现了软开关。 由于LLC 谐振变换器发生谐振,谐振电容Cr两端的电压波形呈正弦规律变化。这些都与理论分析是完全一致的,说明设计的主电路参数是正确的。
输出电压波形如图7 所示,从图中可以看出,输出电压的纹波比较小,输出电压比较稳定。 用SABER 自带的示波器测量工具测得输出电压的平均值为4 054.1 V,仿真所得的实际电压与要求的4 000 V 电压非常接近,精度比较高。
以上仿真结果表明,前面的理论分析是正确的,主电路各部分参数设计是合理的,本文所设计的微波加热用磁控管电源是可行的,说明了本文所做的工作是有意义的,对于微波加热电源领域具有很大的实际参考价值。
5 结 论
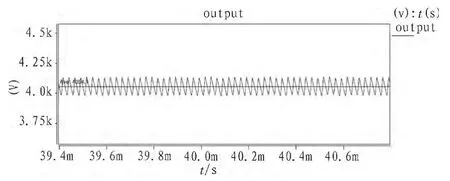
图7 输出电压波形Fig. 7 The output voltage waveform
文中采用半桥LLC 谐振变换器和倍压整流相结合的方式设计了一款微波加热用磁控管供电电源,利用基波分析法对主电路进行了建模分析,完成了LLC 谐振变换器的核心参数设计,并提出了一种从根本上解决变压器偏磁饱和问题的解决方案,用仿真软件SABER 对所设计的主电路进行仿真,验证了理论分析的正确性。 仿真结果表明该设计方案可以让半桥LLC 谐振变换器主电路可靠高效工作, 实现软开关,可以作为负载磁控管的供电电源。
[1] 李新卫. 微波加热器磁控管电源的研究与设计[D]. 山东科技大学,2009.
[2] 赵敏杰,戴瑶,张怀武. LLC谐振变换器的参数设计[J]. 磁性材料及器件,2011(2):53-57,72.
[3] 才琳,孙耀杰,高骞,等. 磁控管电源系统研究与设计[J].电子设计工程,2011(23):154-155,159.
[4] 李宗朝. 大功率微波电源控制方案的研究[D]. 武汉工程大学,2013.
[5] 徐勤超,王春芳,李从洋. LLC谐振式磁控管供电电源的研究[J]. 电力电子技术,2010(10):106-108.
[6] 杨威,郑宏伟,陈文光. 工业微波磁控管开关电源系统设计[J]. 真空电子技术,2013(1):53-55,66.
[7] 牛斌. 微波高功率源输出功率稳定技术的研究[D]. 东南大学,2006.
[8] 余昌斌. LLC谐振半桥DC-DC变换器的研究[D]. 重庆大学,2007.

