一种低复杂度的均峰功率比抑制技术--PSM

王 直， 马 踔

（江苏科技大学 电子信息学院， 江苏 镇江 212003）

由于OFDM 技术具有可以有效的抵抗频域选择性衰弱，并且频谱利用率较高等优点，所以该正交频分技术一直备受人们关注。 但是，传输信号较高的峰均功率比（PAPR）一直是OFDM 技术的主要缺陷。 因为较高的峰均功率比会大大削弱移动终端设备电池的寿命。

以前的学者提出了许多解决OFDM 信号峰值功率问题的方法，如在文献[1-2]中提出的选择性映射（SLM）和部分发送序列 （PTS）， 这两种方法相比与其他方法， 能够在抵制OFDM 信号峰值功率的时候，不会引入任何的干扰，同时不会使噪声放大。 但是，这两种方法共同有的一个缺点是，它们要从生成的大量备选信号中选取峰值功率较小的一个进行发送，从而使得运算复杂度较高。 为了克服SLM 和PTS 的这一缺点，一些学者提出了相应的低复杂度算法。 如在文献[4]中提出的改进IFFT（Inverse Fast Fourier Transform）算法以及在文献[5]中提出的转换矩阵算法。 转换矩阵算法是利用矩阵降低运算复杂度， 但同时这些矩阵也会减小某些载波的功率，导致了系统性能降低。基于文献[5]提出的算法，wang 和其他学者选取了12 个矩阵， 这些转换矩阵不会改变载波的功率。 但是，这个算法最多只能生成12 个备选信号，所以在一定程度上，影响了该算法的性能[6]。 在文献[7]中，一些学者提出利用DFT （Discrete Fourier Transform） 的特性来避免IFFT多余的运算。 文献[8]中提出通过循环移位序列方式实现利用更多的级，性能与PTS 方法相似。 上述的方法仍然需要大量的乘法运算，复杂度依然很高。

文中提出了一种复杂度较低的方法-PSM （Partial Shift Mapping），部分位移映射方法，它与SLM 相似，用较低的峰值功率产生备选信号。 利用DFT 变换特性，PSM 只需要一次IFFT 运算没有额外复杂的乘法就可以产生这些备选信号，从而实现了降低算法复杂度。 同时仿真分析证明本论文提出的方法可以有效的抑制峰值功率。

1 系统模型与DFT 性质

设表示OFDM 的并行码元符号，即在k 子信道中发送的信号（k=0，1，…，N-1），N 代表子信道的数量。 因此OFDM 信号经过IFFT 采样调制后可以表示为：

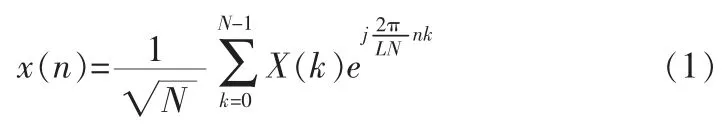
其中，L 为采样系数， 精确测量信号的峰值功率。 所以，OFDM 信号的峰值功率比PAPR 定义为最大瞬时功率与平均功率的比值，即

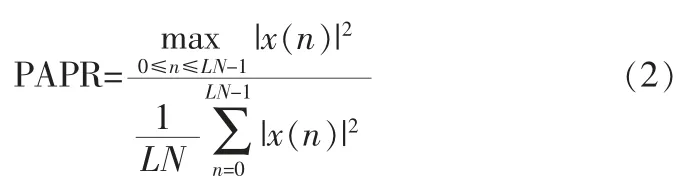
下面介绍DFT 变换性质在OFDM 信号中的应用，设fi（i=0，1，2，3），表示4 个长度为LN 的序列，即

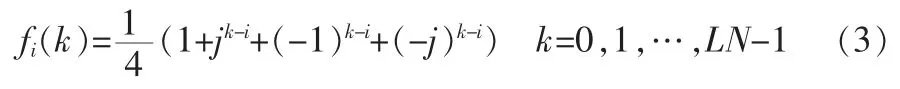
其中，fi（k）是fi中的一个元素，可以推导为f0=[1，0，0，0，1，0，0，0…，1，0，0，0]，fi是f0右循环移位i 次所得到的序列。因此，序列fi包含的所有序列即为原始的OFDM 符号序列。X（k）可以被分为4 个不相交的子数据块，每个子数据块都以非零元素开始，被fi（k）序列加权后得到：

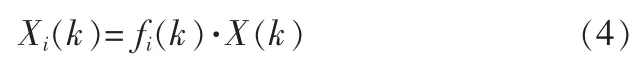
性质1：

时域信号xi（n），由上述公式（4）中Xi（k）经过一次IFFT运算得到，即：

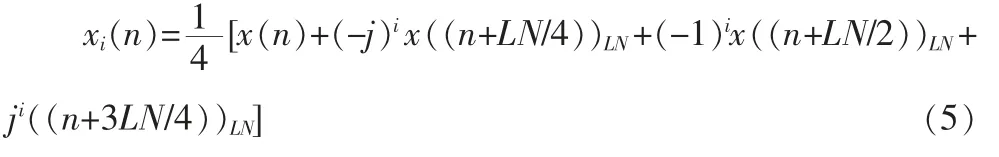
其中，（·）LN为模-LN 运算符。 基于性质1，每个子数据块Xi（k）的时域信号，可以通过一次IFFT 运算生成x，然后x 与其循环位移（LN/4，LN/2 与3LN/4）相加产生减少了大量复杂的乘法运算，有效地降低了复杂度。 文献[3，8]所述的PTS 方法，生成子数据块时域信号的方法是通过在每个子数据块上应用IFFT 变换实现的。 因此，得到的每个子数据块的时域信号与PTS 相比只应用了一次IFFT 变换。

性质2：

根据DFT 的移位性质，可以得知时域信号x（n）的循环移位等价于频域信号X（k）的相移，即

在本文提出的PSM 方法中， 备选信号由时域信号xi（n）循环位移得到。 因此，备选信号也可以由频域信号X（k）各个子块相移产生。所以本算法产生时域信号避免了大量的IFFT变换和复杂的乘法运算。

2 本文提出的PSM（峰值功率抑制技术）方法

图1 显示的是该方法的原理图，如图所示，采样时域信号x（n）是由并行输入信号经过IFFT 运算后生成，然后根据性质1 生成4 个分组时域信号xi（n）。 详细过程如图2（a）中所示，首先时域信号x（n）乘1/4，然后进行循环位移，根据位移的不同步数（LN/4，LN/2，3LN/4）生成相应的信号。 因此，这些分组的时域信号的产生是根据公式（5），即由位移后的时域信号与原始时域信号的1/4 相结合生成的。

图1 PSM 算法系统框图Fig. 1 Block diagram of PSM scheme

这些分组时域信号经过结合器后生成一系列备选信号如图2（b）所示。 本文提出的PSM 算法产生备选信号是通过将分组时域信号xi（n）（i=1，2，3）进行循环位移得到。 其中，预定步数，lm，i为第m 个备选信号第i 个分组信号的位移步数。本文中，lm，i将 随机选择1 到LN 中的整 数，然后与xi（n）相加生成备选信号，因此，第m 个备选信号为：

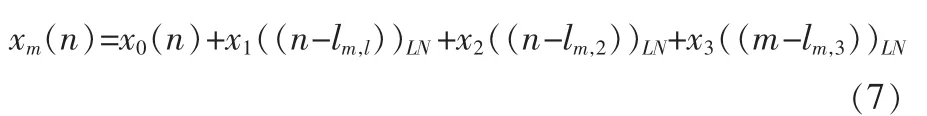
从公式（8）我们可以看出，这些备选信号就等于X1（k），X2（k），X3（k）相位移动加权。 由于在不同子模块的子载波相互分离， 所以这也意味着在每个子载波上的信号的功率是恒定的。 子数据块功率和将不会影响的每个子载波的功率。因此，PSM 可能不会降低OFDM 通信系统的误码率，与公式（5）中的转换矩阵算法相反。 最后，M-1 个备选信号与初始信号的PAPR 值可以计算出，然后选出PAPR 值最低信号进行传输。

和SLM 一样，被选中传输的备选信号的序号一定要做为边信息发送到接收机用以恢复原始数据， 因此， 根据公式（8），频域信号相位旋转。 根据边信息，可以用在子信道上相移的离散的信号恢复出原始数据。 边信息对于接收机恢复出原始数据非常重要，所以它一定要通过一个可靠、有效的方式被发送到接收机。

3 复杂度分析与仿真

由图1 可知，PSM 方法生成想x（n）信号要进行一次LN点的IFFT 运算，其中，（LN/2）log2LN包括次复数乘法与（LN/2）log2LN次复数加法，另外，生成时域分组信号xi（n）还需要12LN 次复数加法和3（M-1）次分数加法生成备选信号。 从表格1 中可以看出，SLM，PTS 的乘法复杂度是PSM 的M 或V倍。其中，V 是PTS 中分组信号的数量。因此可以看出，在PTS中，复杂度会随着备选信号的数量成倍的增加。 图3 显示为SLM 与PSM 之间复杂度的比较， 其中载波数量是1 024，过采样率为4。 可以看出，PSM 的乘法复杂度没有随M 的增加而增加。

要注意的是， 在PSM 中， 可以用相似的方法和性质将OFDM 符号分成4 个以上的分组，但是，这种情况会引进多余的乘法运算，而且在性能上也没有得到很大改善。 所以，在本文所提出的PSM 方法中，主要选择4 个分组进行研究。

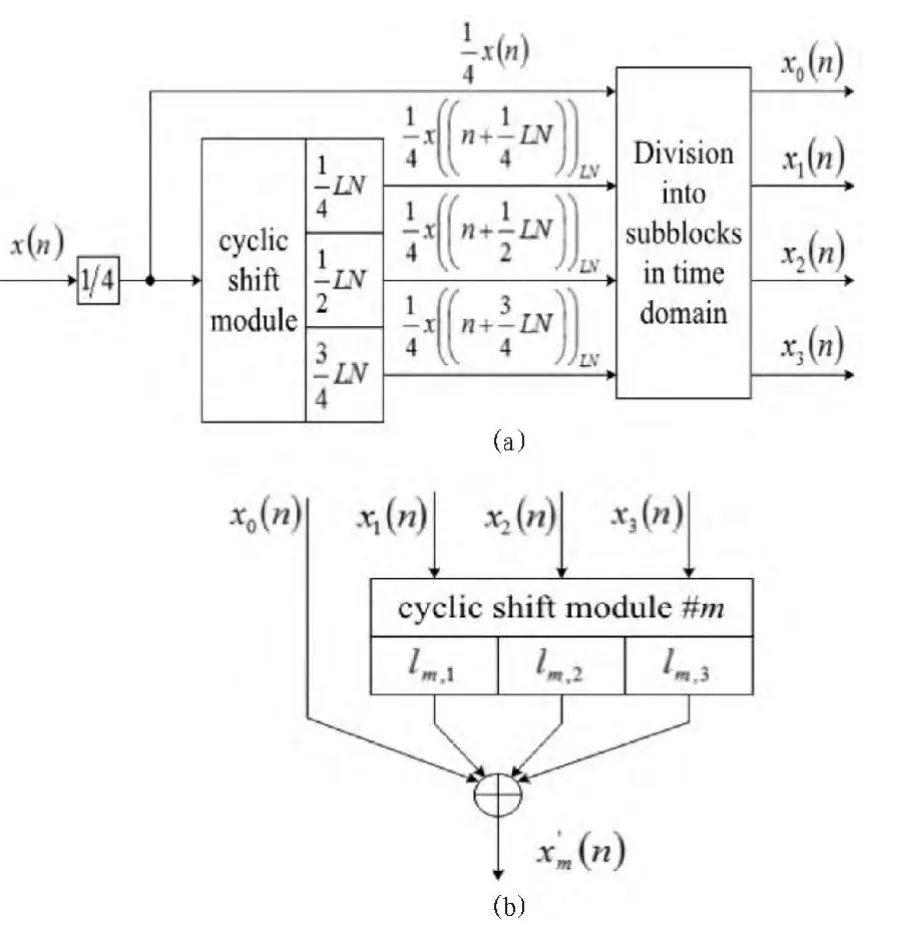
图2 PSM 中（a）分场算法框图和（b）第m 个合并器框图Fig. 2 （a）Architecture of block of dividing into disjointsubblocks and（b）architecture of m-th combiner

图3 复数加法和乘法运算与备选信号的数量关系Fig. 3 Complex operations as a function of the number ofcandidate signals M （LN=4，096）

我们通常用PAPR 的互补积累分布函数来描述PSPR 的特性。 在图4 中显示出了PTS，SLM 和PSM 经过QPSK 载波调制后的特性曲线。 在PSM 中，位移步数lm，i在1 到LN-1 之间随机选取一个数。当备选信号个数M=8 和16 时，SLM，PTS与PSM 性能十分相似， 但是SLM 的乘法运算量是PSM 的8和16 倍。 当M=16，V=4 时，PTS 比PSM 差大约0.3 dB，但是PTS 的乘法运算量是PSM 的4 倍。而且，要生成64 个备选信号来选出最佳的一个，这样就导致大量额外的运算量和更多的数据位来索引备选信号。

图5 中显示出了PSM 与图4 中所提出的低复杂度SLM算法的性能比较，PSM 算法在IFFT 多级蝶形运算中， 在第k级引入SLM 算法。 所以，当k 为0 时， 它将变为一般的SLM算法，当k 接近最后一级n 时，它的复杂度将降低，但是它的性能也随之有所下降。 由图5 可知，当k 接近5 的时候，它的性能相似于PSM。 然而它的复杂度大约是PSM 的8.48 倍，当M=16 时。

表1 SLM、PTS 与PSM 的运算复杂度Tab. 1 Computational complexity of SLM，PTS and PSM

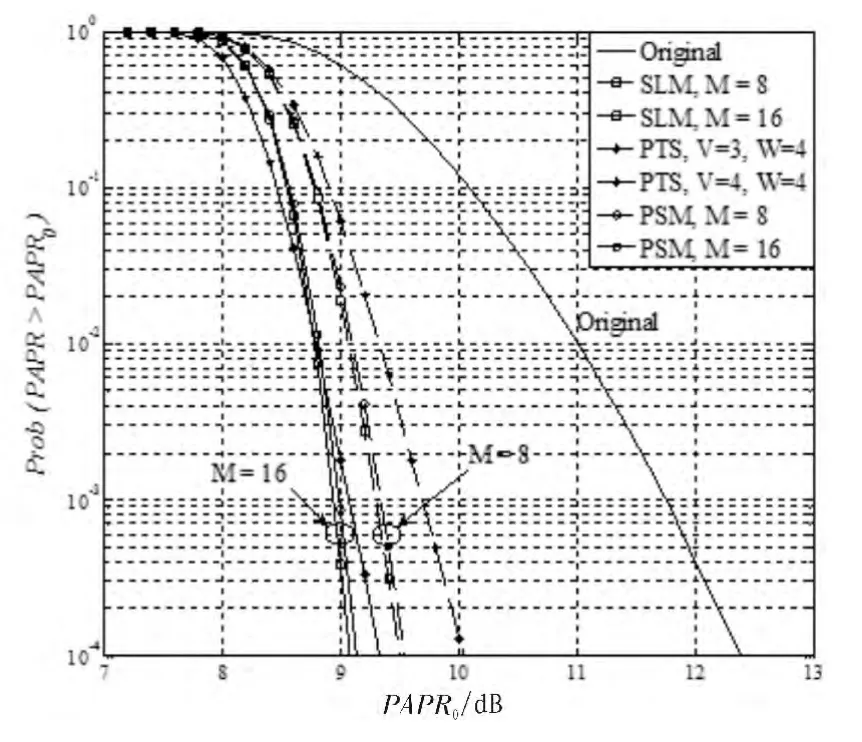
图4 SLM、PTS 与PSM 的PAPR 性能曲线Fig. 4 PAPR reduction performance for SLM， PTS，and PSM（N=1，024， L=4）

图5 低复杂度的SLM 与PSM 的PAPR 性能曲线Fig. 5 PAPR reduction performance for reduced complex SLM，proposed in [4]， and PSM （N=1，024， L=4）

还有一些其他的仿真结果，在文中没有一一展示，同样也证明了PSM 的PAPR 特性与SLM 相似， 但是比PST 性能优越； 在PSM 中不同的备选信号均有同一线性相位因子加权生成。 在PTS 中，备选信号的相关性是最高的，这也导致其最不理想的性能表现。

4 结 论

本文提出了一种OFDM 系统低复杂度的PAPR 抑制技术-PSM。 该技术基于DFT 和OFDM 信号的性质，在时域生成备选信号，从而避免大量的IFFT 运算，在一定程度上减少了运算量，并与SLM 有相似的性能。 从仿真结果我们分析得到，在相同的条件下，当备选信号数量为16 时，PSM 与SLM 性能相似，而复数加法和乘法的运算量仅为SLM 的6.25%和35%。

[1] Tao J，Wu Y. An Overview: Peak-to-Average power ratio reduction techniques for OFDM signals[J]. IEEE Trans.Broadcast.，2008，54（2）:257-268.

[2] Bäuml R，Fischer R，Huber J. Reducing the peak-to-average power ratio of multicarrier modulation by selected mapping[J].Elect. Lett.，1996，32（22）:2056-2057.

[3] Müller S H，Huber J B. A novel peak power reduction scheme for OFDM[J]. Proc. IEEE PIMRC， Helsinki， Finland，1997:1090-1094.

[4] Lim D W. A new SLM OFDM scheme with low complexity for PAPR reduction[J]. IEEE Signal Process. Lett.，2005，12（2）:93-96.

[5] Wang C L，Ouyang Y. Low-Complexity selected mapping schemes for peak-to-average power ratio reduction in OFDM Systems[J]. IEEE Trans. Signal Process.，2005，53（12）:4652-4660.

[6] Wang C L，Ku S J. Novel conversion matrices for simplifying the IFFT computation of an SLM-Based PAPR reduction scheme for OFDM systems[J]. IEEE Trans. Commun.，2009，57（7）:1903-1907.

[7] Lu G，Wu P，Aronsson D. Peak-to-Average power ratio reduction in OFDM using cyclically shifted phase sequences[J].IET Commun.，2007（6）:1146-1151.

[8] Hill G，Faulkner M，Singh J.Cyclic shifting and time inversion of partial transmit sequences to reduce the peak-to-Average power ratio in OFDM[J]. Proc. IEEE PIMRC， London， UK，Sept. 2000:1256-1259.