基于改进极限学习机的纱线质量预测

杨建国,熊经纬,徐　兰,吕志军

(东华大学 机械工程学院,上海 201620)

基于改进极限学习机的纱线质量预测

杨建国,熊经纬,徐兰,吕志军

(东华大学 机械工程学院,上海 201620)

由于随机给定输入权值和偏差,极限学习机(extreme learning machine, ELM) 通常需要较多隐含层节点才能达到理想精度.结合粒子群算法具有全局搜索能力的优势,提出一种基于改进ELM算法的纱线质量预测模型,采用改进粒子群算法优化ELM 算法的输入权值矩阵和隐含层偏差,计算出输出权值矩阵,以减少隐含层节点数.试验结果表明,相比于ELM算法,改进ELM算法能够依靠更少的隐含层节点获得更高精度, 相对误差降低2.70%,可为纱线质量预测与控制提供更有效的工具,具有广泛的推广实用性.

极限学习机；纱线质量；粒子群算法；质量预测

纺织工艺参数与加工质量之间存在着复杂的非线性、离散型和模糊的关系.纺织加工是一个依赖于领域专家知识与经验的思维过程.同其他工业领域相比,智能化方法在纺织生产中的应用还相对滞后.纺织生产中积累了大量工艺数据和质量数据,但蕴含在这些数据中的隐性工艺知识却难以获取和重用.国外已开始使用神经网络技术进行纱线质量预测研究与应用[1-2],国内也有对于毛条、纺纱、织造和后整理加工质量进行预测的研究[3-4].针对毛纱CV值预测问题,大多采用基于前馈人工神经网络的优化模型或支持向量机的优化分类模型,但由于其存在迭代次数过多及易陷入局部最优等缺点,迫切需要一种新的方法来为纺纱质量预测提供不同的视角.

文献[5]提出新型单隐层前馈神经网络极限学习机(extreme learning machine, ELM),其与传统神经网络的区别在于可调参数少,只需设置隐含层节点数,再通过随机给定的输入层隐含层的连接权值与隐含层阈值得到输出层权值矩阵,通过网络对数据样本的训练便能够得到唯一的最优解,因此，ELM的优点是泛化性能好以及学习速度快等[6-9].文献[10-13]将ELM算法应用于汽轮机故障诊断、供水管网故障智能诊断、断路器振声时联合故障诊断、航空发动机传感器故障诊断、电力故障检测等方面，均获得了较好的效果.ELM算法的最终输出权值矩阵是通过计算随机给出的权值和偏差得到的,而输入权值与隐含层偏差是随机给定的,这样存在的问题就是随机给定的值可能为0,导致部分隐含层节点在整个网络中不起作用[14-15].因此在实际的工程应用中,只有通过不断增加隐含层节点数才能得到理想的精度,这样就降低了算法在预测上的精度.针对以上问题,本文利用改进的粒子群算法来优化ELM输入权值与隐含层偏差的选取,达到消除无效的隐含层节点、提高网络的学习能力与泛化性能的目的.

1　改进粒子群算法

(1)

(2)

式中:ω为惯性权重,用来调节对解空间的搜索范围;d=1, 2,…，D，i=1, 2,…,S,D为待优化问题的维数,S为种群大小;k为当前迭代次数;vid为微粒速度;c1和c2(非负常数)为学习因子,决定了粒子的搜索与收敛能力;r1和r2为两个相互独立的随机数,取值范围为(0, 1),以增加搜索随机性.为降低粒子在迭代过程中脱离搜索空间的概率,一般将其位置和速度限制在[-Xmax,Xmax]、[-vmax,vmax].

1.1学习因子的改进

在粒子群算法中,学习因子表示粒子相互之间交流能力的强与弱,并且决定算法最终收敛的结果,其值过大或过小都将影响算法的学习与收敛能力,因此，选取一种学习因子动态调整的策略,其更新计算如式(3)与(4)所示.

(3)

(4)

式中:k为算法的当前迭代次数,kmax为算法的最大迭代次数.由式(3)与(4)可知,在算法的初期阶段c1随迭代次数的增加而递减,c2随迭代次数的增加而递增.因此，在迭代刚开始的阶段,学习因子的变化可以提高粒子的全局搜索能力,而在末期,则提高粒子收敛到全局最优的能力.

2　基于改进极限学习机的预测模型

改进ELM算法流程如图1所示.

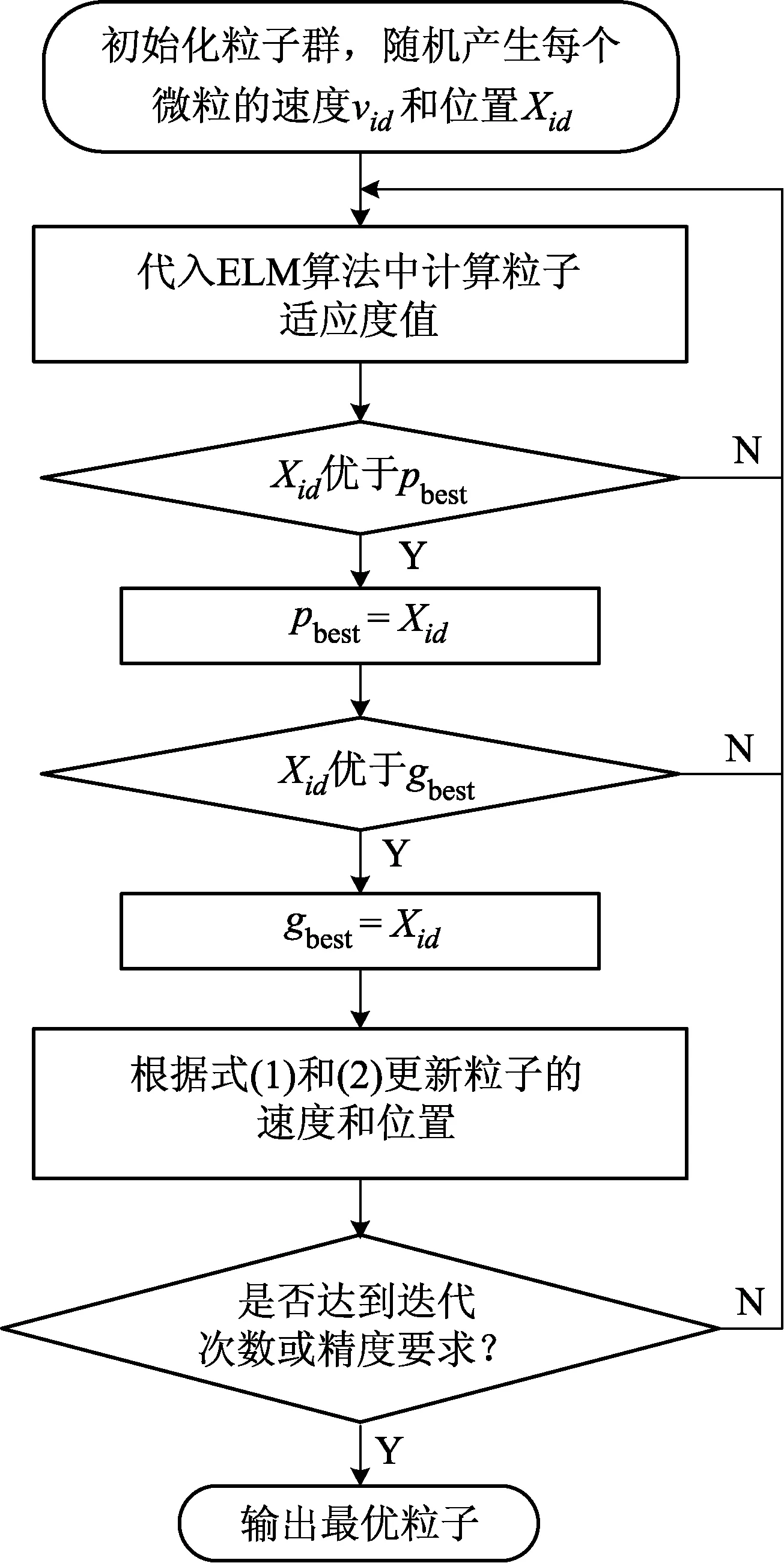
图1　改进ELM算法流程图Fig.1　Improved ELM algorithm flow chart

改进ELM算法实现过程如下：

(1) 初始化粒子群.主要是初始化粒子群算法的关键参数,包括种群的规模(即粒子的数量)、粒子的初始化速度、迭代的次数,其中粒子的数量一般为20～40,网络的输入连接权值矩阵与隐含层偏置值矩阵构成粒子的全部结构.同时初始化粒子群的速度v,并限定v∈[-vmax,vmax],迭代次数取100.

(2) 将粒子群中的每个粒子带入 ELM 算法,计算出预测结果与实际结果的平均相对误差,将其作为更新粒子速度与位置的依据,即为粒子的适应度值.本文中,改进ELM算法的隐含层激活函数选取 Sigmoid 函数.

(3) 寻优.寻优的过程就是一个迭代的过程,将粒子的适应值作为粒子更新的依据.首先计算出任意一个粒子的适应度值,记为p1,令pbest=p1；再计算出第二个粒子的适应度值p2,若其优于pbest,则pbest=p2,并且将pbest的位置更新为第二个粒子的位置,并令gbest=pbest,其中gbest为全局最优解,得到第三个粒子的适应度值之后,按同样的操作方法更新个体最优极值与全局最优极值,直到循环结束,得到最佳适应度值及对应的粒子位置.

3　应用实例

3.1试验数据准备

精梳工序是毛纱的生产瓶颈,它的生产状态好坏制约着产品的最终质量,本文以某公司生产过程中毛纱CV值的预测为例说明改进ELM算法的实现过程.已知某公司纱线生产数据如表1所示,建立毛纱CV值的预测模型,其中输入参数为直径离散(离散系数)、粗纱捻系数、毛条含油量、纤维质量不匀率、毛条回潮率、纤维长度(豪特长度LH)、纤维直径、细纱车速、细纱钢丝圈号、细纱牵伸倍数.输出参数为毛纱CV值,数据表中选取1～30条作为训练数据集,第31～36条作为模型测试数据集.

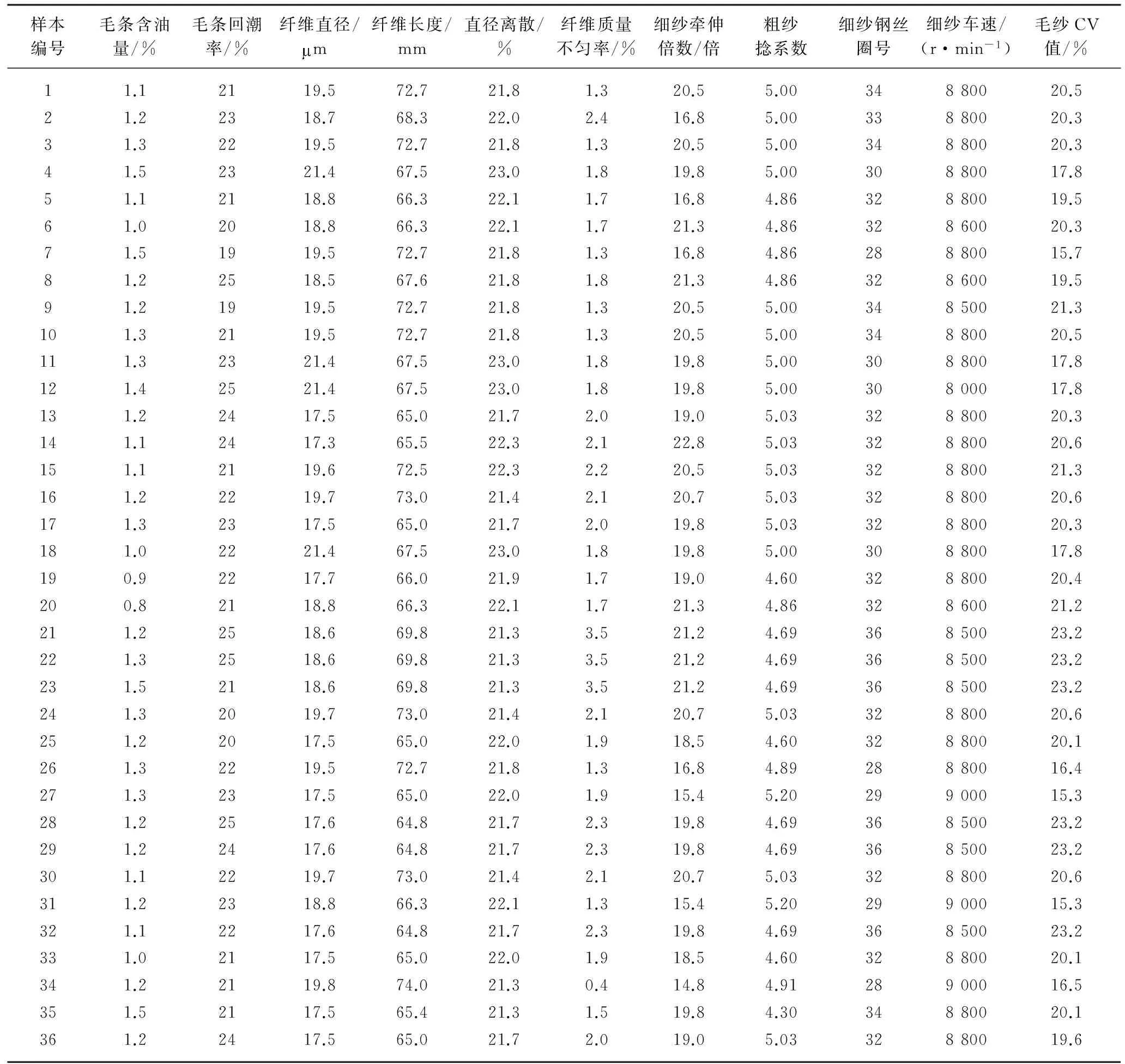
表1　精梳毛纱CV值生产质量数据Table 1　The production quality data of worsted yarns CV value

3.2改进极限学习机的性能分析

运用Matlab软件编写改进ELM算法程序.改进ELM算法中各参数设定：种群个数S=20,最大迭代次数kmax=100,学习因子c1与c2由式(3)与(4)在程序运行的过程中实时更新,惯性权重ω=0.8, 激励函数为Sigmoid,隐含层节点数为100.适应度函数值如图2所示.由图2可知,随着迭代次数的增加,适应度函数值逐渐减小,在达到68代之后,其逐渐达到稳定状态,约为1.8%,此时每个个体都是在最优解的附近.

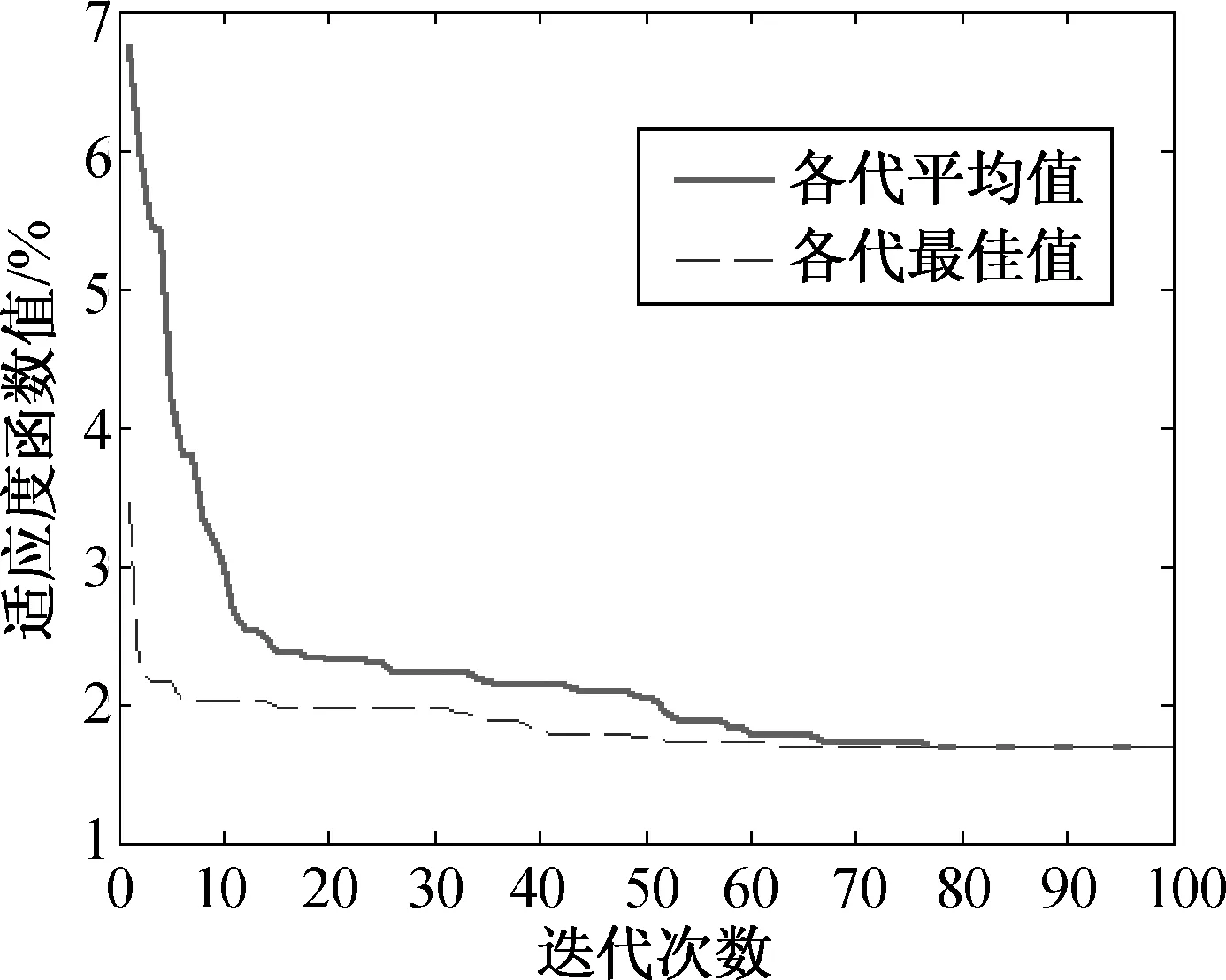
图2　改进ELM算法适应度函数迭代进化过程Fig.2　The fitness function iterative evolution process of improved ELM algorithm

隐含层节点数对ELM算法与改进ELM算法的影响如表2所示.由表2可以看出,两种算法的平均相对误差都随着隐含层节点数的增加先降低再升高.当ELM算法与改进ELM算法的平均相对误差达到最小时,其隐含层节点数分别为3 000与200,相差巨大,且ELM算法的最小误差大于改进ELM算法的最小误差,说明改进ELM算法在预测精度上具有更优的性能.在隐含层节点数为200时,ELM算法的运行时间为0.35 s, 改进ELM算法运行时间为24.7 s,虽然传统ELM算法的速度更快,但无法达到改进ELM算法的高精度效果.

表2　隐含层节点数对ELM算法与改进ELM算法的影响Table 2　Influence of hidden layer nodes number on ELM and improved ELM algorithm

为了比较改进的ELM算法在纺纱质量预测上的优势,同时利用传统的BP(back propagation)算法、ELM算法对数据样本进行训练,并采用另外12组样本数据进行预测,3种算法预测对比结果如表3所示.

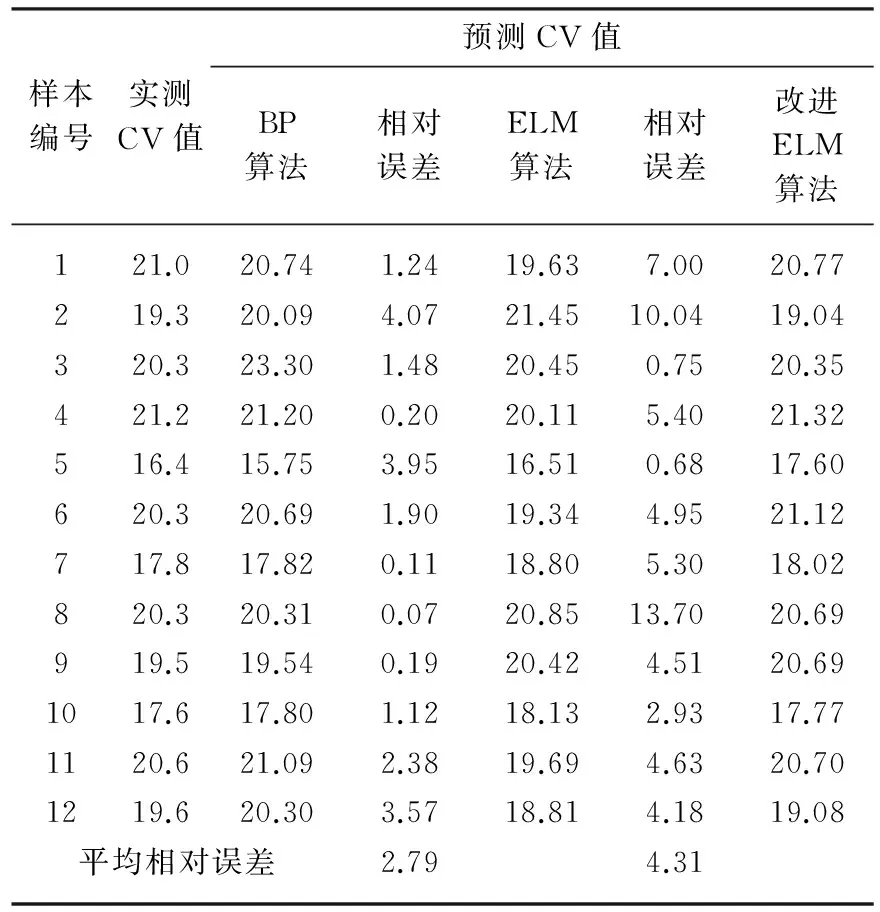
表3　3种算法预测精梳毛纱CV值比较Table 3　Comparison of worsted yarns CV value prediction by three kinds of algorithms　%

由表3可以看出,改进ELM算法平均相对误差相比于BP算法与传统ELM算法分别降低1.18%与2.70%,且从单个样本的预测误差波动上来讲,改进ELM算法的波动幅度最小,说明其稳定性在3种算法中也是最佳的.

4　结　语

针对ELM算法模型在纱线质量预测上存在的缺点,本文将改进粒子群算法与ELM算法相结合,用以优化ELM输入权值与隐含层偏差的选取.试验结果表明,同传统ELM算法相比,改进ELM算法能够用更少的隐含层节点数使纱线质量预测达到更高的精度,且其预测稳定性能也有所提高；同传统BP神经网络相比,其预测精度更高,对于工艺人员实时优化工艺参数,节约生产成本有着重要的借鉴作用.

[1] CHUNG F, JEFFERY K, KUN I, et al. Using neural network theory to predict the properties of melt spun fibers [J]. Textile Research Journal, 2004, 74(9): 840-843.

[2] ERTUGRUL S, UCAR N. Prediction bursting strength of cotton plain knitted fabrics using intelligent techniques [J]. Textile Research Journal, 2000, 70(10): 845-851.

[3] 项前,杨建国,程隆棣.基于支持向量机的纱线质量预测[J]. 纺织学报,2008,29(4):43-46.

[4] 董奎勇,于伟东.基于人工神经网络的毛精纺纱线质量预报技术[J].毛纺科技,2002(2):3-6.

[5] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine:Theory and applications [J]. Neurocomputing, 2006, 70(1/2/3): 489-501.

[6] CAO J W, LIN Z P, HUANG G B. Self-adaptive evolutionary extreme learning machine [J]. Neural Process Letters, 2012,36(3): 285-305.

[7] 李小冬.核极限学习机的理论与算法及其在图像处理中的应用[D].杭州:浙江大学控制科学与工程学院,2014.

[8] 潘红芳.极限学习机的研究及其在醋酸精馏软测量建模中的应用[D].上海:华东理工大学信息科学与工程学院,2014.

[9] 廖洪一,王欣.基于极限学习机的股票价格预测[J].计算机与现代化,2014(12):19-22.

[10] 蒋丹,赵书涛,赵现平,等.基于极限学习机的断路器振声时联合故障诊断方法[J].智能电网,2014,2(8):8-12.

[11] 高相铭,刘付斌,杨世凤.基于极限学习机的供水管网故障智能诊断方法[J].计算机工程与设计,2013,34(8):2887-2891.

[12] 孙毅刚,刘静雅,赵珍.基于极限学习机的航空发动机传感器故障诊断[J].传感器与微系统,2014,33(8):23-26.

[13] 李远景.基于极限学习算法的HVCD电力故障检测方法[J].电气开关,2014(4):36-38.

[14] 程松, 闫建伟, 赵登福,等.短期负荷预测的集成改进极端学习机方法[J].西安交通大学学报,2009,43(2):106-110.

[15] LIANG N Y, HUANG G B. A fast and accurate online sequential learning algorithm for feed forward networks [J]. IEEE Transactions on Neural Networks, 2006, 17(6): 1411-1423.

Yarn Quality Prediction Based on Improved Extreme Learning Machine

YANGJian-guo,XIONGJing-wei,XULan,LÜZhi-jun

(College of Mechanical Engineering, Donghua University, Shanghai 201620, China)

Due to the randomly-given input weights and deviation, extreme learning machine (ELM) often needs more hidden layer nodes to achieve ideal precision. By combining with particle swarm algorithm which has the advantage of global searching ability, a kind of improved ELM yarn quality prediction model is proposed. Besides, the input weight matrix and the hidden layer deviation of ELM algorithm are optimized by using the improved particle swarm optimization. In addition, the output weight matrix is calculated to reduce the number of hidden layer nodes. The test results show that the improved ELM can rely on fewer hidden layer nodes to obtain higher precision than the ELM algorithm, and the improved ELM decreases by 2.70% of relative error， so it can provide more effective tool for yarn quality prediction and control and has extensive promotion practicality.

extreme learning machine; yarn quality; particle swarm algorithm; quality prediction

1671-0444(2015)04-0494-04

2015-05-20

国家自然科学基金资助项目(51175077)

杨建国(1951—),男,上海人，教授,博士,研究方向为智能制造、质量控制. E-mail:jgyangm@dhu.edu.cn

TH 16.2

A