用模拟退火算法拟合铂电阻的热特性曲线
张佳仁 张婧瑜 王 鹏 张建忠 / 上海市质量监督检验技术研究院
用模拟退火算法拟合铂电阻的热特性曲线
张佳仁张婧瑜王 鹏张建忠 / 上海市质量监督检验技术研究院
介绍了模拟退火算法的基本原理,阐述了该算法拟合曲线的一般步骤。针对JJG 229-2010 《工业铂、铜热电阻检定规程》,在最小二乘法的基础上,利用模拟退火算法拟合铂电阻的热特性曲线,分析了这一算法在拟合过程中的稳定性。结果表明:模拟退火优化算法同样适用于曲线拟合过程,拟合过程的稳定性有待进一步研究。
模拟退火算法;铂电阻;曲线拟合
0 引言
铂电阻是工业过程中普遍使用的温度传感器。铂电阻的热特性曲线可以被描述为电阻与温度之间的函数关系,也是反映其非线性特征的重要依据[1]。在工业铂、铜热电阻的计量校准工作中,拟合电阻-温度关系的回归方程是一项重要的工作,也是研究的热点。在以往的研究中,诸多学者都基于不同的进化算法,对铂电阻的非线性特征进行了回归化拟合的研究,并取得了令人满意的结果[2,3]。
拟合回归方程的传统方法是最小二乘法。作为最为传统的数学优化技术,最小二乘法通过最小化误差的平方和获得目标函数的回归方程。利用最小二乘法可以简便地求得未知的数据,并使这些数据与实际数据之间误差的平方和为最小。不过,该方法作为一种被动性优化技术,也有其限制条件:样本中测量值的个数要多于拟合曲线参数的个数;自由度越小,最小二乘法的拟合可靠度也越低。
近年来,在最小二乘法的基础上,众多学者建立了许多启发式的优化技术,包括:遗传算法、蚁群算法、退火模拟算法等[4]。本文利用模拟退火算法拟合热电阻的特性曲线回归方程。
1 模拟退火算法
模拟退火算法最早由N. Metropolis 等人于1953年提出。1983年,S. Kirkpatrick 等成功地将退火算法引入到组合优化领域[5]。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法,其出发点是物理中固体物质的退火过程与一般组合优化问题之间的相似性。
模拟退火算法是通过赋予搜索过程一种时变且最终趋于零的概率突跳性,从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。模拟退火算法从某一较高初温出发,伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。求解优化问题的模拟退火算法与固体退火过程的模拟比较如表1所示。

表1 模拟退火算法与固体退火过程的模拟比较
模拟退火算法的一般步骤是:
1)产生一个位于解空间的新解。通常选择由当前新解经过简单变换即可产生新解的方法,如对构成新解的全部或部分元素进行置换、互换等。
2)计算与新解所对应的目标函数差。因为目标函数差仅由变换部分产生,所以目标函数差的计算最好按增量计算。对大多数应用而言,这是计算目标函数差的最快方法。
3)判断新解是否被接受。判断的依据是一个接受准则,最常用的接受准则是Metropolis准则。
4)当新解被确定接受时,用新解代替当前解,这只需将当前解中对应于产生新解时的变换部分予以实现,同时修正目标函数值即可。此时,当前解实现了一次迭代,可在此基础上开始下一轮试验。而当新解被判定为舍弃时,则在原当前解的基础上继续下一轮试验。
模拟退火算法与初始值无关,算法求得的解与初始解状态无关,具有渐近收敛性。该算法已在理论上被证明是一种收敛于全局最优解的全局优化算法,具有并行性[6]。
2 最优步长的计算
在选择模拟退火算法作为优化策略的前提下,最优步长的选取是决定优化过程有效与否、收敛速度快慢的关键。本文利用牛顿法作为最优步长的计算方法。
牛顿法是一种函数逼近法,其基本思想是:在极小点附近用二阶泰勒多项式近似代替目标函数,从而求出函数极小点的估计值,公式证明:

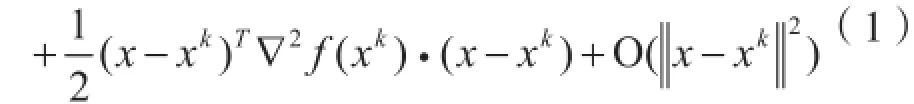
又记:
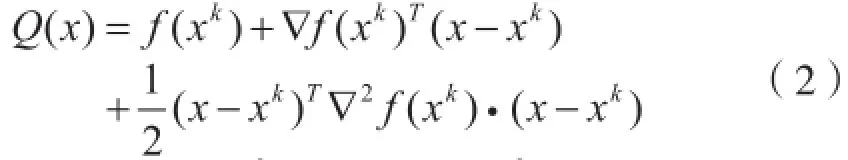
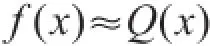
记:
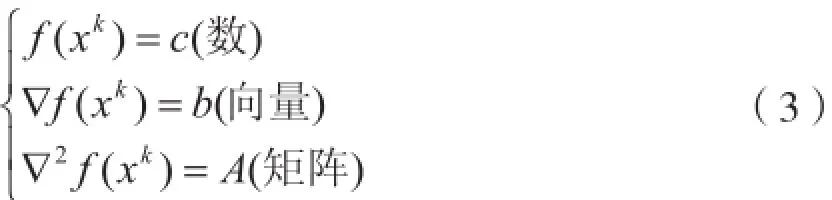
将式(3)代入式(2)有:

对式(4)求导,得:


将式(3)代入式(6)有:由式(7)可知:牛顿法的最优步长为矩阵,搜索方向为矩阵 。

3 铂电阻热特性曲线的拟合
根据JJG 229-2010 《工业铂、铜热电阻检定规程》,铂电阻的电阻-温度关系可以表示为

本文结合最小二乘法,利用退火模拟算法拟合铂电阻热特性曲线,即电阻-温度的函数关系。作为启发式的优化技术,退火模拟算法主动搜索优化方向,使目标函数的值无限小,迫使误差不断趋近于零,非线性特征不断逼近测量数据。
3.1建立曲线拟合优化过程的目标函数
目标函数即为各温度点上铂电阻阻值的实测值与拟合值的差:


式中:X — 各待定常数的矩阵表达式
3.2优化策略
优化策略的核心:1)给定优化变量的初始解;2)沿着合适优化路径不断迭代优化变量,迫使目标函数沿着最优的方向行走;3)当目标函数无限趋近于零时,设置优化终止条件,得到最优解。具体步骤如下:

(4)如果迭代终止条件满足,则算法结束,当前解为最终解,否则重新进入(3)步骤。
4 拟合示例
以pt100型铂热电阻分度表为例,在0 ~ 200 ℃范围内,均匀取20个数据作为拟合曲线的采样数据,利用退火模拟算法对采样数据进行曲线拟合,对比拟合曲线与实际数据的偏差。
在0 ~ 200 ℃温度范围内,铂热电阻的阻值-温度关系可以描述为为铂电阻在温度t时刻的阻值,(a,b,c)为待定常数,即优化变量。初始解设定(1,1,100),收敛条件设定为
最终的拟合公式为


图1 标准电阻值与拟合结果的偏差图
从图中可以看出:全温度范围内的拟合结果是比较理想的。但是,标准值与拟合值的差值在整个范围内不断地正波动,波动的范围随温度的上升而扩大,在180 ℃领域内出现了较大的波峰。出现该现象的原因:模拟退火算法是一种启发式随机性算法,计算机生成的随机数也是均匀分布的,这就导致优化方向和路径在某概率区间内随机分布,也随之不断波动。此外,优化过程仅对目标函数的整体误差建立了收敛条件,并未单独处理各温度点上的收敛性,这也导致波动范围的不可控。
5 结语
作为一种尝试,本文在拟合铂电阻热特性曲线中引入了模拟退火算法,得到了比较理想的结果。同时,该结果也揭示了优化过程中的一些问题:标准值与拟合值在整个范围内不断波动;波动的范围随温度的上升而扩大,波动范围不可控。这些问题有待进一步研究。
[1] 姚丽芳, 陈宇, 郑伟, 等.精密铂电阻温度计的校准方法[J].上海计量测试, 2014,04:21-25.
[2] 刘天键, 王劭伯, 朱善安.基于神经网络的铂电阻温度传感器非线性校正方法[J].仪器仪表学报,2002, 05:518-521.
[3] 李俭川, 张文娜, 果明明.基于神经网络的热电偶特性数学模型[J].传感器技术,2000,01:18-20.
[4] 梁旭,黄明. 现代智能优化混合算法及其应用[M]. 北京:电子工业出版社,2011.
[5] Diego Lanzi. Frames as choice superstructures[J].The Journal of Socio-Economics, 2011, 40:115-123.
[6] Xinpeng Du, Lizhi Cheng, Daiqiang Chen. A simulated annealing algorithm for sparse recovery by minimization[J].Neurocomputing,2014, 131:98-104.
The explore to fit RTD characteristic curve by Simulated annealing algorithm
Zhang jiaren, Zhang jinyu, Wang pen,Zhang jianzhong
(Shanghai Institute of Quality Inspection and Technical Research)
The basic principle of the simulated annealing algorithm,described the general steps of the algorithm curve fitting. On the basis of JJG 229-2010“Verification Regulation of Industry Platinum Copper Resistance Thermometers” and the least squares method, using simulated annealing algorithm to fit platinum resistance characteristic curve analysis of the stability of this algorithm in the fitting process. The results showed that: simulated annealing optimization algorithm is equally applicable to the curve fitting process, the stability of the fitting process for further study.
simulated annealing algorithm; RTD; curve fitting

