影响分汊河道纵向离散的因子权重及相关性研究
顾 莉,王兰兰,华祖林1,,褚克坚1,
(1. 河海大学浅水湖泊综合治理与资源开发教育部重点实验室,南京 210098; 2. 河海大学水资源高效利用与工程安全国家工程研究中心, 南京 210098; 3. 河海大学环境学院, 南京 210098)
· 试验研究 ·
影响分汊河道纵向离散的因子权重及相关性研究
顾莉1,2,3,王兰兰3,华祖林1,3,褚克坚1,3
(1. 河海大学浅水湖泊综合治理与资源开发教育部重点实验室,南京210098; 2. 河海大学水资源高效利用与工程安全国家工程研究中心, 南京210098; 3. 河海大学环境学院, 南京210098)
河流纵向离散系数是反映污染物在河流中纵向离散特性的关键性参数。前人研究主要针对顺直和弯曲河道,对于水流结构与边界条件更为复杂的分汊河道研究甚少。本文采用分类回归树(CART)挖掘技术结合示踪试验数据,对分汊河道的不同流速,分流比,宽度比,宽深比及壁面糙度等共108个工况的试验进行分析,研究了各变量因子对于纵向离散系数影响的重要程度,量化了各影响因子的权重大小,其中流速的影响权重最大、其次分流比与宽度比并列,宽深比次之,壁面糙度影响最小;此外,还分析了纵向离散系数与各因子间的响应关系,流速正相关,宽深比负相关,分流比或宽度比等于0.5,即两汊对称情形下离散系数最小。研究成果对于了解与掌握分汊型河道纵向离散特性具有重要意义。
分汊河道;纵向离散系数;分类回归树;影响因子权重;相关性
纵向离散系数反映了河流中污染物的掺混能力,对确定河流的纳污能力和污染物扩散过程至关重要,纵向离散系数的研究一直以来受到学者们广泛关注[1~4]。研究纵向离散系数的常用方法有理论公式、示踪试验以及经验公式法[5~10]。近年来,由于计算机技术的发展,一些学者开始采用各种统计类数学模型来估算河流纵向离散能力,模糊逻辑、自适应神经模糊推理技术、支持向量机、人工神经网络,M5’ 模型及人工智能[11~16]等方法都被应用于对纵向离散系数的估算。前人的研究多针对单一的顺直和弯曲型河道,且研究结果多是得到离散系数的量值或计算离散系数的公式,而对于影响因子对纵向离散系数影响的相对重要程度研究很少,尤其是对边界和水流条件更为复杂的分汊型河道的研究更为少见。分汊河道的研究多为其河床演变规律、分流比计算方法、水沙运动特征,以及分汊口与交汇口的水动力特性[17],还有少量关于污染物在分汊口或交汇口的浓度分布规律研究[18,19]。分类回归树(CART)模型可以分析变量之间的相互作用,识别对响应变量的变化具有显著贡献的参量。分类回归树(CART)模型最早由Breiman等人[20]提出,已经在统计领域和数据挖掘技术中广泛应用,但是在环境水力学方面未见使用。
本文针对分汊河道纵向离散特性开展研究,利用室内示踪试验数据,采用分类回归树方法,在对影响离散系数变量分析过程中,通过反复验证,给出了各变量对于纵向离散系数影响的相对重要性,并分析了各变量与纵向离散系数之间的相关关系,从而深入了解分汊河道的纵向离散能力。
1 分类回归树(CART)方法基本原理
CART方法是一种二元递归分解方法,可以产生基于树的模型[20]。树的构建可以看作是一个变量选择的过程,所有问题可以归结为两点:选择哪个变量作为拆分点以及怎样拆分。选择变量及选择变量分裂点的标准是使得分裂点的不纯度最小,CART算法中使用基尼系数Gini(T)来衡量节点的不纯度,基尼系数计算步骤[21]如下:
(1)假设训练集中有N类样本X1,X2,…,Xj,…,XN,每类样本的样本容量为n,根节点的基尼系数为
(1)
式中:Pj为j类样本在总体中概率,T为相应的树。
(2)指定分组变量的某个取值为分割阈值,计算各组的基尼系数,再加权平均值基尼系数,即
(2)
其中,j[1,N]为样本分类,i[1,n]为每类样本的样本容量
(3)计算根节点与其下一层基尼系数加权值的差值:
△=Gini(T)-Ginisplit(i)(T)
(3)
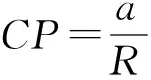
2 数据来源及结果分析
2.1数据来源
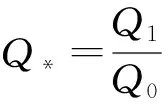
2.2结果分析
本文使用分类回归树方法(CART)对双汊型河道纵向离散特性进行研究,分类回归树方法可以给出影响变量的相对重要性,这是由于分类回归树法存在如下特性:(1)变量的重要性表现为该变量出现在树干的起始部位,或离起始部位很近;(2)重要性还表现为同一变量多次在模型中出现。

图1 实验设备平面布置示意Fig.1 Schematic layout of experimental model

表1 实验工况
在确定影响因子重要性之前,首先需要构建决策树,并结合数据特点,确定出影响程度大的主要因子,排除影响小的次要因子。图2是原始情况下的决策树,是将所有的影响因子作为输入变量得到的,此时的决策树比较复杂,图形难以辨认。因此,必须对决策树进行剪枝,图3(a)给出了模型复杂性参数图,由图3(a),模型在4次分解前,交叉验证误差随着分解次数的增加迅速减少,而接下来的模型相对误差处于波动状态,因此,选择CP=0.02将模型进行简化,简化后的决策树见图3(b)。
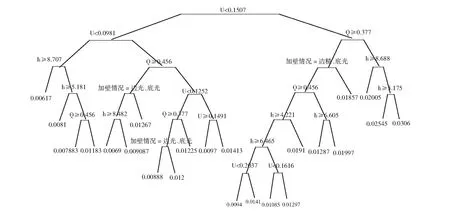
图2 原始分类回归树Fig.2 Classification and regression tree of original data

图3 参数复杂性(CP)图及剪枝后决策树(a为CP图,b为剪枝后决策树)Fig.3 The figure of CP and prune classification and regression tree(a. figure of CP; b. prune CART)
对于图3(b),每个节点的数值,表示的是纵向离散系数Kx在这种情况下的平均值,n表示108个工况中被分入该类的工况数,因为在剪枝过程中,经过反复的交叉验证,删除了对树贡献较小的变量,因此修剪后的树的节点变量可能会发生变化,每个节点处的分类变量,表示当Kx在该范围时,此变量对Kx的影响较大。对于给定数值的工况,在画出决策树后,决策者可以根据树形图的走向很容易预测未知因变量的取值范围,以图3b为例,当在U<0.0981,h≥8.707时,Kx的值约为0.006,而当0.0981≤U<0.1507,h<8.707时,Kx的值约为0.009,以此类推,可以得出其他情况下的Kx取值。
表2给出了当所有变量均作为输入变量以及减少某种输入变量时,各输入变量的权重大小。由表2可知,对纵向离散系数影响最重要的因子为平均流速U;而分流比与宽度比对纵向离散系数影响的相对重要性参数相同;宽深比对于纵向离散系数的影响相较于平均流速U,分流比和宽度比都小;而对纵向离散系数影响最小的变量为边壁情况。

表2 变量的影响权重值
通过结合变量的影响权重值和决策树可进一步分析各变量与纵向离散系数的关系。在得出变量影响权重后,对于重要性相同的因子通过进一步分析可知其是否为非独立变量。由图4a与图3b,在不考虑分流比影响时,宽度比替代了分流比,而节点的纵向离散系数值始终未改变,而不考虑宽度比时,生成的决策树与图3b完全相同(图略),由于在本实验中两支汊水深与流速差异很小,且支汊断面为矩形,所以分流比和宽度比呈正相关,两者为不独立变量,所以当输入变量中无宽度比时,其他变量的相对重要性值与无分流比时相同,两种情况下分流比与宽度比的相对重要性相同,见表2。
当缺少变量宽深比时,比较图4b和图3b可知,除平均流速为U的节点外,其他节点变量均被宽度比所替代,且决策树的树形图与图3b也有所差异,可见,宽深比的相对重要性虽没有平均流速U,分流比,宽度比大,但是其仍占有一定比重,且宽深比为独立变量,所以当变量宽深比缺失时,会对结果产生明显影响,因此在输入变量选择时要考虑宽深比。
对于影响权重小的变量,在分析中若缺失这些变量将不会对结果产生显著影响,仍可以得到较可信的结果。如不考虑边壁情况作为决策树的输入变量时,决策树也与图3b完全相同,因为边壁情况对纵向离散系数影响较小;当同时不考虑次要变量和非独立变量时,仍可以不对分类结果产生明显影响,图3b与图4c的分类结果也是相同的,由表2也可以看出,在输入变量无宽度比和边壁情况时,对其他变量的权重量值改变不大。
在实际工作中,得到大量数据后,可先通过分类回归树进行变量筛选,得到对结果影响显著的变量,去除噪声变量后,再进行分析,可以得到更为直观准确的结果,从而避免了由于数据过于冗杂,导致计算结果精度差,缺少针对性的现象。

图4 剪枝后的CART图(a为输入变量无分流比,b为输入变量无宽深比,c为输入变量无宽度比及边壁情况)Fig.4 The figure of prune classification and regression tree(a. input variable without diversion ratio; b. input variable without width-depth ratio; c. input variable without width ratio and roughness of side and roughness of bottom )
此外,由分类回归树方法生成的决策树,每个分支均可读出该分支节点变量与纵向离散系数之间的相关关系,如图4a(U<0.1507时Kx等于0.009而当U>0.1507时Kx等于0.02,),纵向离散系数与平均流速呈递增关系,这是由于水流运动越快,断面流速差异越大,纵向离散系数越大;而纵向离散系数与宽深比呈递减关系,因主河道宽度B0保持不变,所以宽深比对于纵向离散系数的影响可以概括为水深对它的影响,宽深比越小,纵向离散系数越大,即纵向离散系数与水深呈递增关系,因为水深增加,河道中的水流流速分布更加不均匀,导致纵向分散能力增强,离散系数与各变量的相关关系分析结论与文献[23]图示分析的结论一致。由图4a与4c可见,纵向离散系数与分流比和宽度比均呈递减关系,分流比或者宽度比越接近0.5,两汊的宽度以及汊道里的流速分布差异越小,分汊口与交汇口流速分布差异性也随之减小,因此纵向离散系数越小。
3 结 论
本文将分类回归树(CART)方法引入河流污染物纵向离散系数的分析,研究不同变量对分汊河道纵向离散系数的影响,该方法不仅可以量化不同影响因子的权重大小,还可以分析变量与纵向离散系数相关关系。通过对大量繁杂数据的整理分析,确定出影响的主次因子,在对纵向离散系数后续研究中,可重点控制影响重要的变量来提高计算的准确度;且可为分汊型河流中水污染防治,排污口设计,纳污能力计算等工作提供理论指导。
[1]Fischer H B, List E J, Koh R C Y, et al. Mixing in inland and coastal waters[M]. New York: Academic Press,1979.
[2]Seo I W, Cheong T S. Predicting longitudinal dispersion coefficient in natural streams[J]. Journal of Hydraulic Engineering, 1998, 124(1): 25-31.
[3]槐文信,徐孝平. 蜿蜒河道中纵向分散系数的水力估测[J]. 武汉大学学报(工学版),2002, 35(4): 9-12.
[4]Shucksmith J D, Boxall J B, and Guymer I. Effects of emergent and submerged natural vegetation on longitudinal mixing in open channel flow[J]. Water Resource Research, 2010, 46(4): W04504.
[5]Christensen B A. Predicting dispersion coefficient of stream[J]. Journal of the Enviromental Engineering Division-ASCE, 1977, 103(6): 1144-1146.
[6]叶志成. 弯曲河流中纵向混合过程的研究[J]. 华东工学院学报,1985,(34):289-299.
[7]李锦秀,黄真理,吕平毓. 三峡库区江段纵向离散系数研究[J]. 水利学报,2000,(8):84-87.
[8]陈永灿,朱德军. 梯形断面明渠中纵向离散系数研究[J]. 水科学进展,2005,16(4):511-517.
[9]郭建青,李彦,王洪胜,等. 确定河流水质参数的抛物方程近似拟和法[J]. 水利水电科技进展,2005,25(2):11-13.
[10]Sahay R R, Dutta S. Prediction of longitudinal dispersion coefficients in natural rivers using genetic algorithm[J]. Hydrology Research, 2009, 40(6): 544-552.
[11]Toprak Z F, and Savci M E. Longitudinal dispersion coefficient modeling in natural channels using fuzzy logic[J]. Clean-Soil Air Water, 2007, 35(6): 626-637.
[12]Riahi-Madvar H, Ayyoubzadeh S A, Khadangi E,et al. An expert system for predicting longitudinal dispersion coefficient in natural streams by using ANFIS[J]. Expert Systems Application, 2009, 36(4): 8589-8596.
[13]Noori R, Karbassi A R, Farokhnia A, et al. Predicting the longitudinal dispersion coefficient using support vector machine and adaptive neuro-fuzzy inference system techniques[J]. Environmental Engineering, 2009, 26(10): 1503-1510.
[14]Sahay R R. Prediction of longitudinal dispersion coefficients in natural rivers using artificial neural network[J]. Environmental Fluid Mechanics, 2011, 11(3): 247-261.
[15]Amir Etemad-Shahidi, and Milad Taghipour. Predicting Longitudinal Dispersion Coefficient in Natural Streams Using M5′ Model Tree[J]. Journal of Hydraulic Engineering, 2012, 138(6): 542-554.
[16]Fuat Toprak Z, Nizamettin Hamidi, Ozgur Kisi, et al. Modeling dimensionless longitudinal dispersion coefficient in natural streams using artificial intelligence methods[J]. KSCE Journal of Civil Engineering, 2014, 18(2): 718-730.
[17]顾莉,华祖林,褚克坚,等. 分汊型河道水流运动特性和污染物输移规律研究进展[J]. 水利水电科技进展, 2011,31(5):88-94.
[18]李克锋,罗麟,李嘉,等.河渠分汊处流量与污染物分配[J].水动力研究与进展,A 辑,1993,8(1):89-96
[19]魏娟,李然,康鹏,等. 水流交汇区污染物输移扩散特性[J]. 水科学进展,2012,23(6):822-828.
[20]Breiman L, Friedman J, Olshen R, et al. Classification and Regression Trees [M]. New York: Wadsworth International Group, 1984.
[21]井彦林,仵彦卿,曹广祝,等.基于数据挖掘技术的黄土分类问题研究[J].岩土力学与工程学报, 2005,(24):4545-4551.
[22]顾莉. 分汊河道污染物输移特性及纵向离散系数的试验研究[D]. 南京:河海大学,2008.
[23]Gu L, Hua Z L, Chu K J, et al. Evaluation of longitudinal dispersion in braided river from transient tracer tests[J]. Fresenius Environmental Bulletin, 2012, 21(3):774.
Study on Weight and Correlation of Impact Factors of the Longitudinal Dispersion in Braided Rivers
GU Li1,2,3, WANG Lan-lan3, HUA Zu-lin1,3, CHU Ke-jian1,3
(1.KeyLaboratoryofIntegratedRegulation&ResourceDevelopmentonShallowLakesofMinistryofEducation,HohaiUniversity,Nanjing210098,China; 2.NationalEngineeringResearchCenterofWaterResourcesEfficientUtilization&EngineeringSafety,HohaiUniversity,Nanjing210098,China; 3.CollegeofEnvironment,HohaiUniversity,Nanjing210098,China)
In the natural river, longitudinal dispersion coefficient is a key parameter to reflect the longitudinal dispersion characteristics of pollutants. Previous researches mainly focused on straight and curved channels, however there had little studies on the braided river with complex flow structures and boundary conditions. In this study, a data mining techniques CART combined with tracer test were used to study the factor importance and factor weights. 108 tests were undertaken, considering different flow velocity, diversion ratio, width ratio, width-depth ratio, roughness of side and roughness of bottom. The results showed that, the greatest impact weight was flow velocity, diversion ratio and width ratio tied for second place, then followed by width-depth ratio, and the roughness impact was minimal. The relationship between longitudinal dispersion and impact factors was also analyzed in this article. Velocity was positive correlated with longitudinal dispersion coefficient, while width-depth ratio was negative related with it. When width ratio and diversion ratio were equal to 0.5(namely the two branches were symmetric), the longitudinal dispersion were minimum. This study results had great significance in the research of the longitudinal dispersion of braided rivers.
Braided river; longitudinal dispersion coefficient; CART; impact factor weights; correlatio
2014-11-17
国家科技支撑计划项目(2012BAB03B04);国家自然科学基金资助项目(51379058,51179052,51479064);水体污染控制与治理科技重大专项课题(2012ZX07103-005);江苏省六大人才高峰计划(08-C)。
顾莉(1981-),女,江苏淮安人,2008年毕业于河海大学环境科学与工程专业,副教授,博士, 研究方向为环境与生态水力学。
华祖林,E-mial:zulinhua@hhu.edu.cn。
X522
A
1001-3644(2015)01-0001-06

