两种常用经验公式法计算水库水温效果比较研究

颜剑波，楚凯锋，张德见，李　璜

(中国电建集团中南勘测设计研究院有限公司，长沙　410014)

两种常用经验公式法计算水库水温效果比较研究

颜剑波，楚凯锋，张德见，李璜

(中国电建集团中南勘测设计研究院有限公司，长沙410014)

大中型水电水利工程建设引起的低温水下泄问题是主要的生态问题之一。目前水库水温计算有经验公式法和数学模型法两大类。指数函数法和余弦函数法是目前水库水温计算两种常用的经验公式方法，也是现有规范推荐的方法。选取了我国11个不同类型的代表性水库，利用实测资料分析研究了两种方法在计算水库水温精度的差异。通过比较研究，笔者建议在有较好的类比水库资料时采用指数函数法，否则建议采用余弦函数法。

水库水温计算；经验公式法；指数函数法；余弦函数法

1　前　言

水电水利工程特别是大中型水电水利工程建成后，水库在沿水深方向上呈现出有规律的水温分层，大致表现为：冬季库区趋于等温分布，下泄水温较天然情况高；春、夏季库表水温高，库底水温低，下泄水温较天然情况低。下泄低温水可对鱼类造成突出的不利影响。水温变冷，水体的溶氧量和水化学成分将发生变化，影响鱼类和饵料生物的衍生，致使鱼类区系组成发生变化。下泄低温水将使鱼类产卵季节推迟、影响鱼卵孵化甚至造成不产卵。下泄低温水还会降低鱼类新陈代谢的能力，使鱼生长缓慢。水温低、饵料生物生长缓慢，将直接影响鱼类的生长、育肥和越冬。低温水会对农作物产生“冷害”影响，造成减产甚至绝产。原国家环境保护总局2005年12月在北京召开了水电水利建设项目水环境与水生生态保护技术政策研讨会，会议形成的“关于印发水电水利建设项目水环境与水生生态保护技术政策研讨会会议纪要的函”(环办函〔2006〕11号)提出关于水库水温的计算主要有：东勘院计算方法(本文中称指数函数法)、中国水科院方法(本文中称余弦函数法)等经验法，以及垂向一维模型、立面二维模型和三维模型等数学模拟法。

总体上，水库水温计算的方法有两大类：经验公式法和数值模型法[1，2]。经验公式法是基于统计学理论建立的方法。数学模型法是基于水库的热量平衡机理建立的方法。理论上，数值模型法计算精度较高，但对基础资料及计算参数率定要求较高[3]。在水电水利工程设计实践工作中，经验公式法仍然是水库水温计算的主要方法，其中应用较多的是指数函数法和余弦函数法。现行水库水温计算相关规范中，《水电水利工程水文计算规范》(DL/T5431-2009)[4]、《水利水电工程水文计算规范》(SL278-2002)[5]推荐指数函数法，《混凝土拱坝设计规范》(SL282-2003)[6]推荐余弦函数法。为了比较这两种经验公式法计算结果的差异，笔者选取了不同调节类型、不同水温结构的水库实测资料进行研究。

2　指数函数法简介

指数函数法计算公式如下：

(1)

(2)

(3)

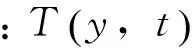
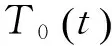
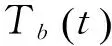
y——水深，m；

m——月份。

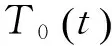
3　余弦函数法简介

余弦函数法计算公式如下：

(4)

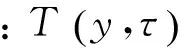
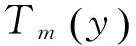
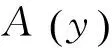
y——水深，m；

τ——时间，月；

τ0——气温年周期变化过程的初始相位，月。纬度高于30°地区，取τ0=6.5月；纬度低于或等于30°地区，取τ0=6.7月;

ω——温度变化的圆频率，ω=2π/12=0.524。

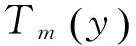
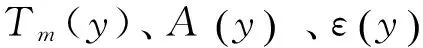
4　案例分析

4.1代表性工程

考虑指数函数法、余弦函数法建立时样本资料的特征，本文选择我国北纬30°左右11个不同类型的代表水库进行研究，包括不同调节性能、不同水温结构的电站水库，见表1。

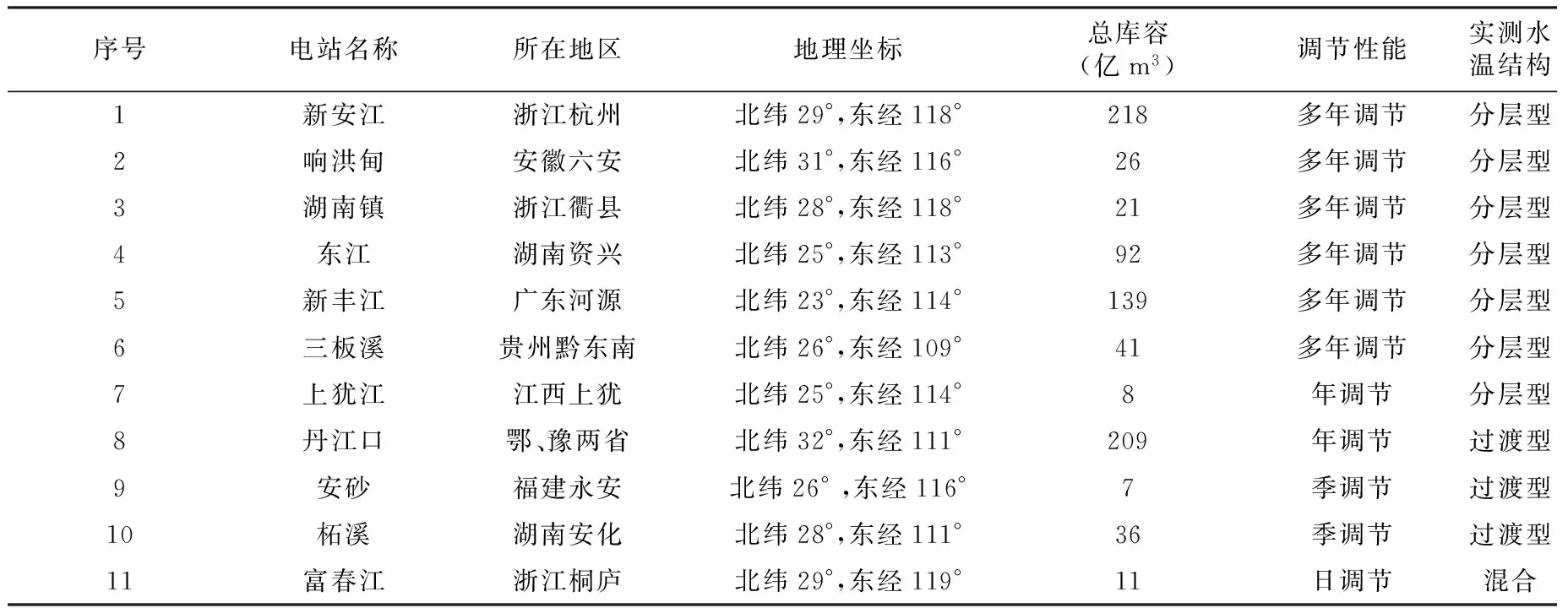
表1　研究选择的代表性电站

4.2水温计算结果比较分析

根据选择的11个代表性水库水温实测资料，分别采用指数函数法、余弦函数法计算水库坝前逐月水温，计算值与与实测值误差见表2。由表2可见，指数函数法计算水库垂向水温误差基本在3℃以内，余弦函数法计算水库垂向水温误差基本在5℃以内。不考虑选择类比水库的误差，理论上指数函数法比余弦函数法有更好的计算精度。

此外，本文分析了两种经验公式计算不同类型水库水温分布曲线的差异，见图1～图4。其中，图1新安江水库代表多年调节的分层型水库，图2凤滩代表年调节的分层型水库，柘溪水库代表季调节的过渡型水库，富春江代表日调节的混合型水库。从水温垂向分布曲线形态来看，指数函数法计算的水温分布曲线更加接近实测水温，这种形态差异是由指数函数、余弦函数不同的插值方法决定的。

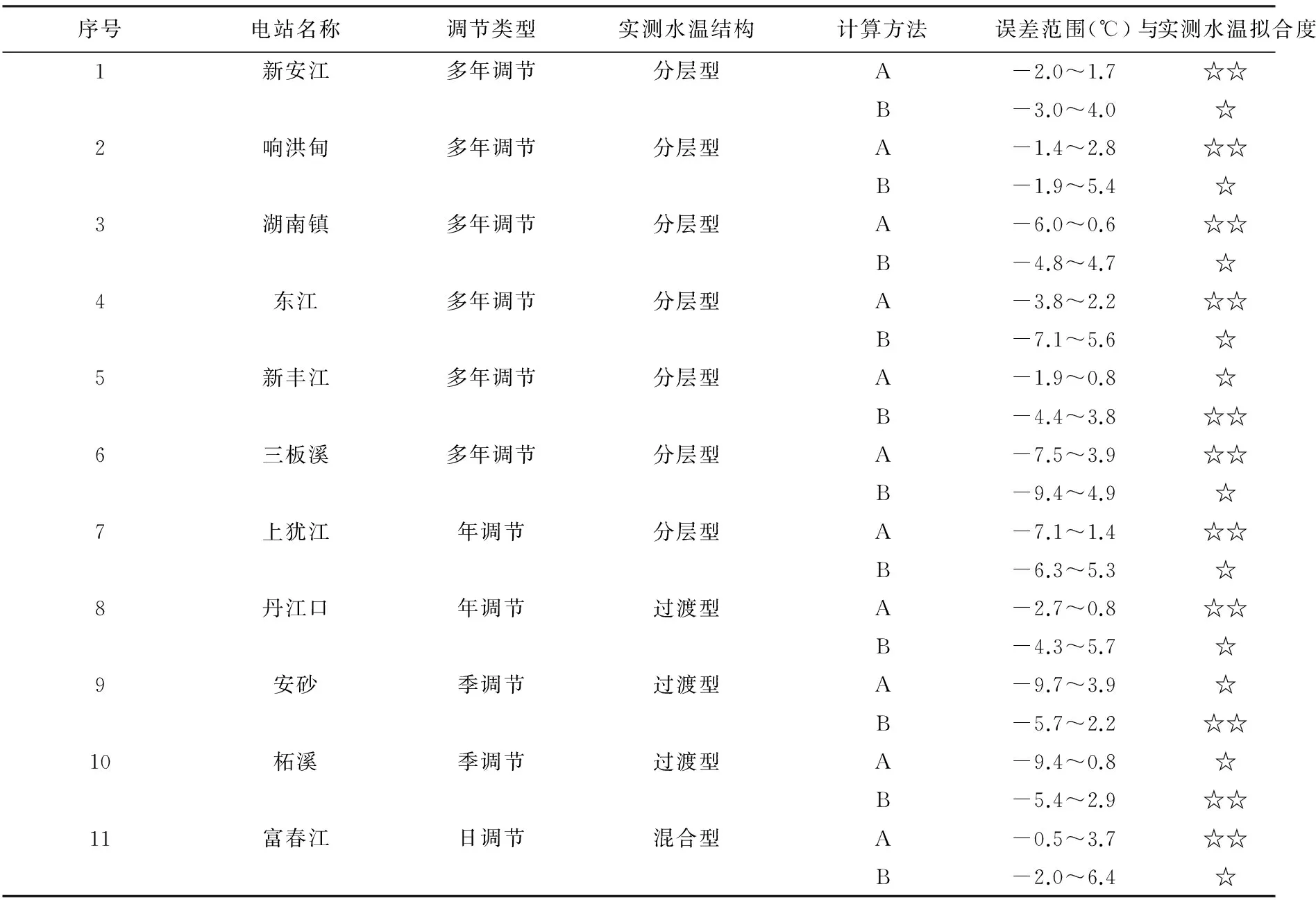
表2　指数函数法和余弦函数法计算水库水温误差比较表

备注：方案A表示指数函数法，方案B代表余弦函数法。☆数量越多代表与实测水温分布拟合度越好。

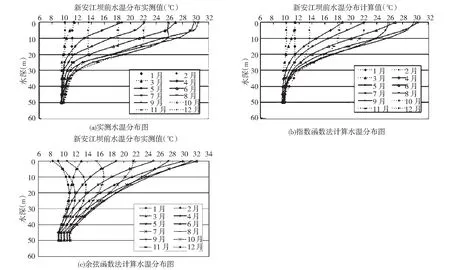
图1　新安江水库Fig.1　Xin’anjiang Reservoir

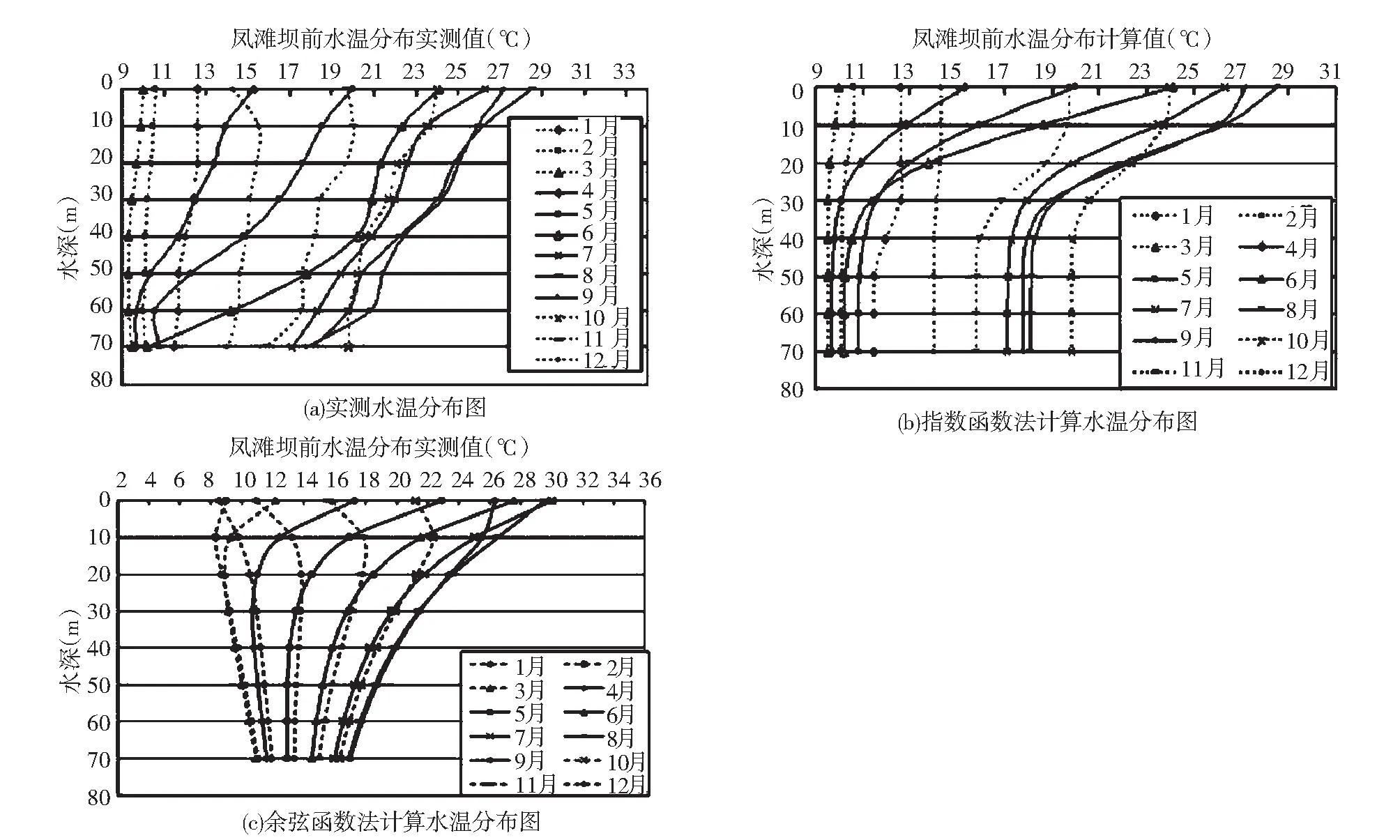
图2　凤滩水库Fig.2　Fengtan Reservoir

图3　柘溪水库Fig.3　Zhexi Reservoir

图4　富春江水库Fig.4　Fuchunjiang Reservoir

5　小　结

水温是评价水环境和水生生态环境变化的一个重要影响因子。水温的变化对水质及水生生物、农田灌溉和生活用水等将产生重大影响。水库水温计算方法有经验公式法和数学模型法两大类。指数函数法、余弦函数法是现有水库水温经验公式计算两种主要的计算方法，也是相关规范推荐的水温计算方法。指数函数法的本质是先求得库表和库底的各月多年平均水温，然后采用指数函数在空间维度上进行插值。余弦函数法的本质是先求得库表至库底任意深度的多年平均水温和年变幅，然后采用余弦函数在时间维度上进行插值。通过选择11个不同类型水库的实测资料分析发现，不考虑类比水库的误差，理论上指数函数法比余弦函数法具有更好的计算精度，计算水温分布曲线形态更加贴合实际。在应用这两种方法进行拟建水库水温预测时，如有较好的类比水库(库容、调节性能、地理位置等相似度高的水库)，本文建议采用指数函数法，否则建议采用余弦函数法。

[1]薛联芳.河流水温数学模型的比较研究[J].水电站设计,1998,14(4)：1.

[2]张仙娥,周孝德,等.水库水温研究方法述评[J].水资源与水工程学报,2006,17(3):1-4.

[3]鞠石泉,苏怀智,等.简述水库水温预测计算方法[J].水电能源科学,2004,22(3):74-77.

[4]DL/T5431-2009,水电水利工程水文计算规范[S].

[5]SL278-2002,水利水电工程水文计算规范[S].

[6]SL282-2003,混凝土拱坝设计规范[S].

Comparative Study of the Water Temperature Calculation of Reservoirs with Two Common Empirical Formulas

YAN Jian-bo, CHU Kai-feng, ZHANG De-jian, LI Huang

(PowerchinaZhongNanEngineeringCorporationLimited，Changsha410014，China)

Low Temperature water discharging problems caused by the construction of large and medium scale hydropower and water conservancy project is one of the major ecological problems. Nowadays, there are two categories method to calculate the water temperature including experienced formula method and mathematical model. The most experienced two methods we had now is Exponential function Method and Cosine Function Method for calculating the water temperature, and they also are the most formal and recommended method. This research project selected 11 representative reservoirs in China, and used actual measuring data of these 11 reservoirs to analysis and research the precision of these two methods and different characteristics. According to our research, we found that we could use Exponential function Method if we have useful and integrated date and information of reservoir, otherwise, we suggest apply Cosine Function Method.

Prediction of water temperature in reservoirs; Empirical formula method; Exponential Function Method Method; Cosine Function Method

2015-06-11

颜剑波(1984-)，男，湖南邵阳人，2009年毕业于河海大学环境工程专业，工程师，研究方向环境影响评价与环境保护工程设计。

X524

A

1001-3644(2015)06-0117-06