定期检修多态退化可修系统的维修更换策略

毋文峰，宋建社，江克侠，李 浩，杨颖涛

（1．第二炮兵工程大学，陕西西安710025；2．武警警官学院管理科学与工程系，四川成都610213；3．武警工程大学理学院，陕西西安710086）

定期检修多态退化可修系统的维修更换策略

毋文峰1，2，宋建社1，江克侠3，李 浩2，杨颖涛1

（1．第二炮兵工程大学，陕西西安710025；2．武警警官学院管理科学与工程系，四川成都610213；3．武警工程大学理学院，陕西西安710086）

针对带定期检修的多状态退化可修系统提出了一种最优维修更换策略。假定系统部件有多个失效状态，并在故障时依概率进入其中某个状态，假定系统检修“修复如旧”和故障维修“修复非新”，系统在检修期间停止工作，检修不影响系统寿命，系统依概率在工作状态、定期检修状态和故障维修状态时达到系统的有效年龄T，在系统更换策略为其有效年龄T的条件下，取系统经长期运行单位时间内期望效益为目标函数，利用推广的几何过程和更新过程理论建立了系统数学模型，并求出了系统期望效益的解析表达式，进一步利用数值法或分析法可以求出最优维修更换策略T＊。该维修更换策略及其模型对于工程实践具有一定的指导意义和参考价值。

几何过程；可修系统；定期检修；多状态系统；更换策略；期望效益

0 引 言

单部件可修系统是可靠性理论与应用领域中的一个重要研究课题，它的维修更换策略研究具有重要的理论意义和经济价值［1］。其中，退化单部件可修系统故障修复是不能“修复如新”的，它被文献［2］描述为一种单调几何过程。目前，“修复非新”退化可修系统是可修系统中的一个热门研究课题，文献［3－9］针对“修复非新”退化可修系统进行了相关研究。若单部件退化可修系统中，假设系统有1个正常状态和K个失效状态，即系统为多状态系统，则该系统称为多态退化可修系统，文献［10］提出了推广的几何过程，用以研究具有多种失效状态的退化可修系统，其他文献还有［11－16］。可修系统在使用和维护中，为了避免重大事故和重大损失的发生，往往还需要考虑定期检修。定期检修主要是为了及时排查系统是否发生故障，因此它一般可视为“修复如旧”的。文献［17］就研究了单部件可修系统的定期检修问题，它是取系统故障次数N为更换策略，求出了系统期望效益的解析表达式，相关文献还有文献［18－19］。

上述文献中系统更换策略大多是取系统的故障次数N，并研究系统期望效益的解析表达式；然而对于军用装备等特殊对象系统，人们更多关心在系统寿命T一定的条件下，系统经长期运行单位时间内的期望效益是否最大。文献［3］虽然是以系统的有效年龄T为更换策略来研究，但是它的目标函数是系统经长期运行单位时间内的平均停机时间是否最小，而且它们只是考虑了比较理想、比较简单的退化可修系统，与实际系统相差较大。因此，针对单部件退化可修系统，作者假定定期检修“修复如旧”和故障维修“修复非新”，考虑系统具有多种失效状态，系统的更换策略取其有效年龄T，并取系统经长期运行单位时间内期望效益最大为目标函数，利用推广的几何过程和更新过程理论研究并确定了最优更换策略T＊，推导了该退化可修系统期望效益的解析表达式。

1 定 义

定义1 假设ξ，η是2个随机变量，如果对任何实数α，有P｛ξ≥α｝＞P｛η≥α｝，则称ξ随机地大于η，记为ξ＞stη。如果ξ随机地小于η，记为ξ＜stη。因此，称一个随机过程｛Xn，n＝1，2，…｝是随机递增（递减）的，如果对所有的n＝1，2，…，满足Xn＜st（＞st）Xn＋1。

定义2 设｛ξ（t），t≥0｝是一个计数过程，｛Xn，n＝1，2，…｝为独立非负随机变量序列，且Xn的分布函数为Fn（t）＝F（an－1t）（n＝1，2，…；a＞0）。若，且满足｛ξ（t）≥n｝＝｛Tn＜t｝（t≥0，n＝1，2，…），则称计数过程｛ξ（t），t≥0｝为一个几何过程，并称Tn为第n个变化时刻，Xn为第n个变化间距。若a＞1，则｛Xn，n＝1，2，…｝是随机递减的；若a＜1，则｛Xn，n＝1，2，…｝是随机递增的；若a＝1，则｛Xn，n＝1，2，…｝为更新过程。

2 基本假定

假定1 初始时（即t＝0），系统是全新的；当系统有效年龄达到T时，用新的同型部件更换系统，并且更换时间可忽略不计。

假定2 Tint为连续2次定期检修之间时间间隔。若系统工作时间达到Tint而未发生故障，修理工立即检修系统，并且检修“修复如旧”；若工作时间未达到Tint而系统故障，修理工立即维修系统，并且维修是“修复非新”的；系统在检修期间停止工作，检修不影响系统寿命。

假定3 系统具有1个正常状态和K个失效状态，失效状态分别记为1，2，…，K，系统随机地进入其中一个失效状态而发生故障；K个失效状态的发生概率分别为r1，r2，…，rK，且r1＋r2＋…＋rK＝1。

假定4 系统从第n－1次故障维修结束到第n次结束之间的时间间隔为其第n个周期（n＝1，2，…），Xn表示系统第n－1次故障维修后的工作时间，Yn表示系统第n次故障后的维修时间，表示系统在第n个周期中第i次检修时间，之间相互独立，记系统第n次故障时刻为tn，故障状态为Sn（Sn∈｛1，2，…，K｝，n＝1，2，…）。假设

式中，lj∈｛1，2，…，K｝（j＝1，2，…，n－1）；a1＞1，a2＞1，…，aK＞1。同样的，假设

式中，lj∈｛1，2，…，K｝（j＝1，2，…，n）；0＜b1＜1，0＜b2＜1，…，0＜bK＜1。假设

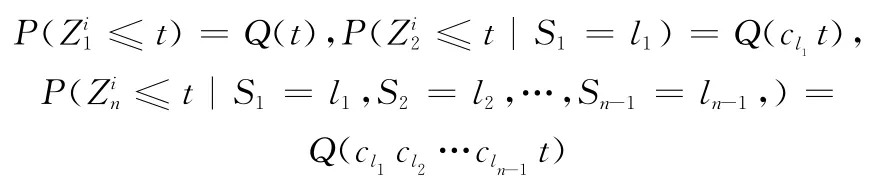
式中，lj∈｛1，2，…，K｝（j＝1，2，…，n－1）；0＜c1＜1；0＜c2＜1，…，0＜cK＜1；i＝1，2，…，ηn，ηn为系统在第n个周期中的检修次数。

假定5 变量Xn，Yn，Zin（n＝1，2，…）之间是相互独立的。

假定6 系统有效年龄在工作状态达到T的概率为p，在定期检修状态达到T的概率为q；在维修状态达到T的概率为r，并且p＋q＋r＝1。

假定7 系统工作报酬率为C1，检修费用率为C2，维修费用率为C3，系统每次更换费用为C4。

3 模型建立

根据模型假定，可以得到系统的一个可能进程图如图1所示。

设D（T）为该系统在上述策略T下经长期运行单位时间内期望效益，由更新报酬定理可得

图1 系统进程图

在讨论模型之前，首先引入几个定理。

定理1 对∀t＞0，n＝1，2，…，有

定理1表明，几何过程｛Xn，n＝1，2，…｝是随机递减的，而几何过程｛Yn，n＝1，2，…｝和｛，n＝1，2，…｝是随机递增的。证明参见文献［10］。

证明见文献［10］。

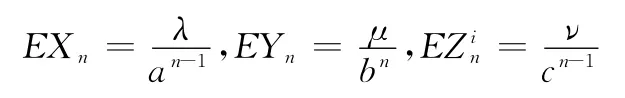
文献［17］提出了可修系统定期检修次数的概率分布，这里，本文提出推广几何过程的检修次数概率分布，它适用于处理多失效状态的退化可修系统模型。

4.统计学处理：采用SPSS 17.0进行数据的整理和统计分析。计量资料用均数±标准差表示，2组之间皮片成活率和平均换药次数的比较因为方差不齐，采用校正t检验。以P<0.05为差异有统计学意义。

定理3 设ηn为系统在第n个周期中的检修次数，则它的概率分布为

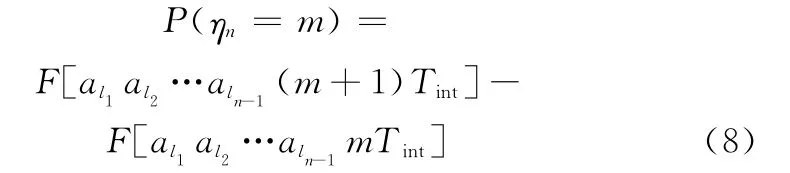
式中，m＝0，1，2，…；n＝1，2，…，N，且

证明 根据假设以及ηn的定义

由于

且广义积分

收敛。因此

证毕

设Zn表示系统在第n个周期中总的检修时间，则

由定理3和条件期望的性质有

设N为系统在［0，T］内的故障次数，它是一个取非负整数的随机变量；事件A、B、C分别表示系统处于工作状态、定期检修状态、故障维修状态时达到T。

（1）事件A

若系统处于工作状态时达到T，则系统正处于第（N＋1）个周期中，如图1（a）所示，设M为系统在第（N＋1）个周期中的检修次数，Tr为系统第（N＋1）个周期的系统寿命，则

且IA＝p，I为示性函数。因此，［0，T］内的期望效益ER 为

（2）事件B

若系统处于定期检修状态时达到T，则系统也正处于第（N＋1）个周期中，如图1（b）所示，同样地，M为系统在第（N＋1）个周期中的检修次数，Tr为系统第（N＋1）个周期的系统寿命，则

且IB＝q。因此，［0，T］内的期望效益ER为

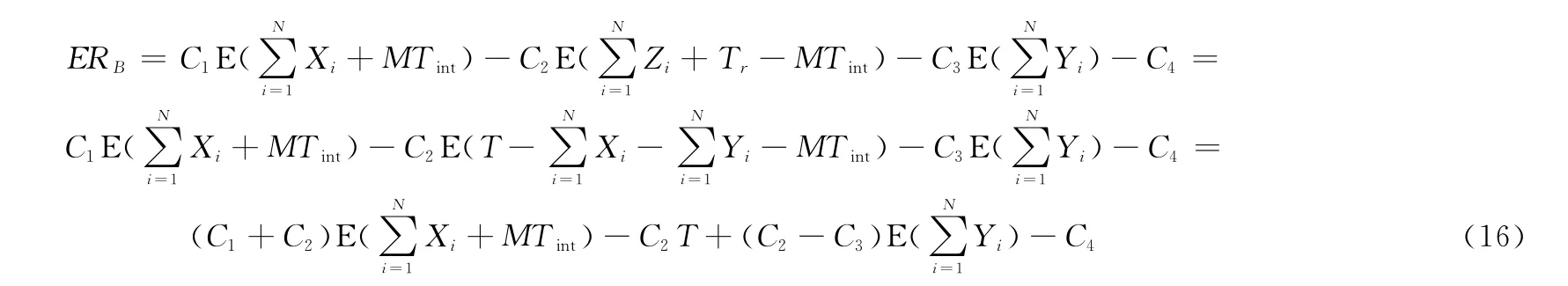
（3）事件C

若系统处于故障维修状态时达到T，则系统正处于第N个周期中，如图1（c）所示，则

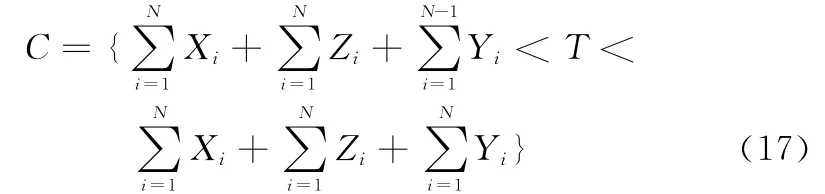
且IC＝r。因此，［0，T］内的期望效益ER为

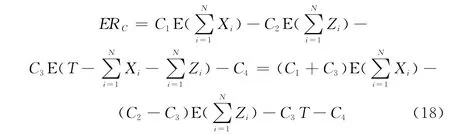
因此，系统在策略T下经长期运行单位时间内的期望效益为

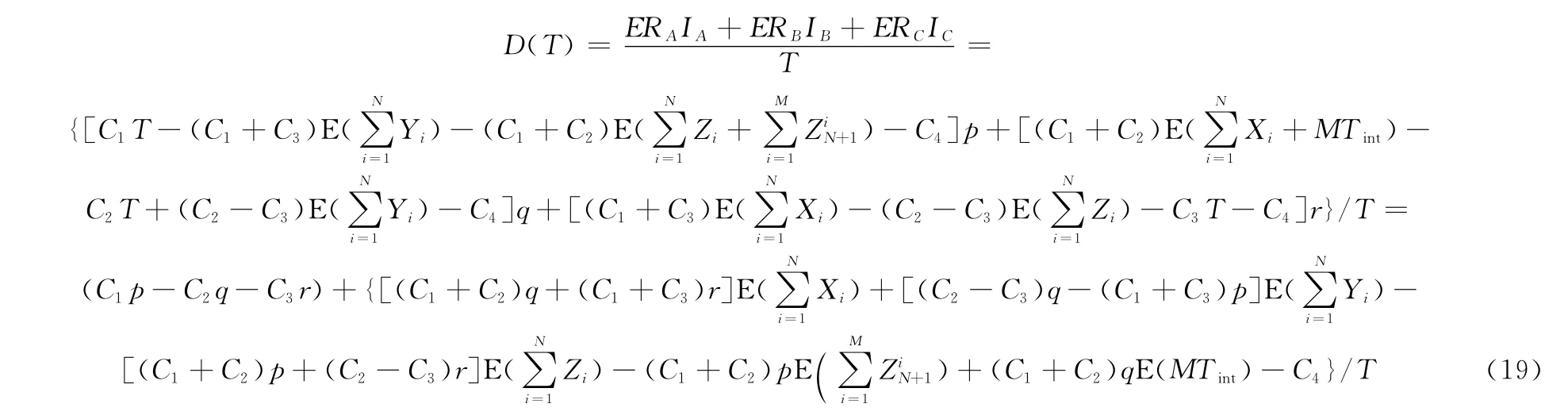
由于

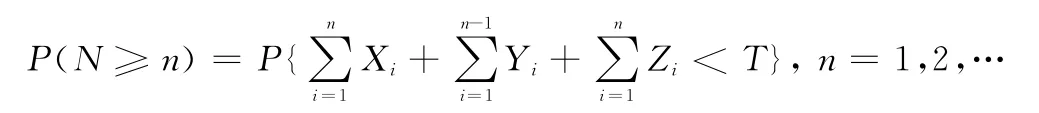
所以

式中

Fn（T），Gn－1（T）和Qn（T）分别为的分布函数，即

由此可得系统在［0，T］内的平均工作时间为

系统在［0，T］内的平均维修时间为

系统在［0，T］内的平均检修时间为

综合上述各式可得

进一步，利用数值法或分析法可以求出最优维修更换策略T＊，并使得该系统经长期运行单位时间内期望效益达到最大。

由于篇幅限制，关于模型的数值仿真实例不再赘述，另篇再叙。

4 结 论

本文带定期检修的多状态退化可修系统的最优更换策略比较具有普适性和实用性，它不仅考虑到了退化可修系统的客观规律，而且还考虑到了系统有效年龄在工作时间、定期检修时间和故障维修时间均可达到的实际，以及系统具有多个失效状态的情况。本文提出的最优更换策略及其模型对于提高对象系统可靠性、安全性和经济效益均具有一定的指导意义和参考价值。

［1］Cao J H，Cheng K．Reliability in mathematics［M］．Beijing：Science Press，2006．（曹晋华，程侃．可靠性数学引论［M］．北京：科学出版社，2006．）

［2］Lam Y．Geometric processes and replacement problem［J］．ACTA Mathematica Applicatae Sinica，1988，4（4）：366－377．

［3］Jia J S，Liu S F，Shang J L．A study on an optimal maintenance policy based on the effective age of the system［J］．Journal ofHenan Normal University（Natural Science），2005，33（4）：10－12．（贾积身，刘思峰，尚江丽．基于系统有效年龄的最优维修策略研究［J］．河南师范大学学报（自然科学版），2005，33（4）：10－12．）

［4］Jia J S，Liu S F，Dang Y G．Study on the optimal replacement policy for a deteriorative repairable system［J］．Systems Engineering－Theory Methodology Applications，2006，15（1）：80－82，89．（贾积身，刘思峰，党耀国．退化可修系统最优更换策略［J］．系统工程理论方法应用，2006，15（1）：80－82，89．）

［5］Jia J S，Wang D S，Duan Z H．Study on the mathematical model under optimal replacement for a deteriorative repairable system［J］．Mathematics in Practice and Theory，2006，36（4）：1－4．（贾积身，王东升，段振辉．退化可修系统最优更换数学模型研究［J］．数学的实践与认识，2006，36（4）：1－4．）

［6］Tan L，Chen T，Guo B．Optimal maintenance strategy for the repairable system consisting of one component based on geometric process［J］．System Engineering，2008，26（6）：88－92．（谭林，陈童，郭波．基于几何过程的单部件可修系统最优维修策略［J］．系统工程，2008，26（6）：88－92．）

［7］Lam Y．A geometric process maintenance model and optimal policy［J］．Journal of Quality in Maintenance Engineering，2013，19（1）：50－60．

［8］Yu M M，Tang Y H，Fu Y H，et al．A deteriorating repairable system with stochastic lead time and replaceable repair facility［J］．Computers ＆Industrial Engineering，2011，62（2）：609－615．

［9］Xiang Y S，Cassady C R，Pohl E A．Optimal maintenance policies for systems subject to a Markovian operating environment［J］．Computers ＆Industrial Engineering，2011，62（1）：190－197．

［10］Lam Y，Zhang Y L，Zheng Y H．A geometric process equivalent model for a multistate degenerative system［J］．European Journal of Operational Research，2002，142（1）：21－29．

［11］Zhang Y L．An optimal replacement policy for a three－state repairable system with a monotone process model［J］．IEEE Trans．on Reliability，2004，53（4）：452－457．

［12］Zhang Y L，Richard C M，Lam Y，et al．A bivariate optimal replacement policy for a multistate repairable system［J］．Reliability Engineering and System Safety，2007，92（4）：535－542．

［13］Moghaddass R，Zuo M J，Pandey M．Optimal design and maintenance of a repairable multi－state system with standby components［J］．Journal of Statistical Planning and Inference，2012，142（8）：2409－2420．

［14］Cheng G Q，Li L，Tang Y H．Optimal replacement policy for a deteriorating series repairable system with multi－state［J］．Sys－tems Engineering－Theory ＆Practice，2012，32（5）：1118－1123．（成国庆，李玲，唐应辉．多态退化串联可修系统的最优维修更换策略［J］．系统工程理论与实践，2012，32（5）：1118－1123．）

［15］Pang Y，Huang H Z，Liu Y，et al．Possibility theory based multi－state system reliability analysis［J］．Journal of Xi’an Jiaotong University，2013，47（3）：75－79．（庞煜，黄洪钟，刘宇，等．多状态系统的可能可靠性分析［J］．西安交通大学学报，2013，47（3）：75－79．）

［16］Wang L H，Yue D Q．On reliability of a multi－state degraded system with minimal repairs and replacement policy［J］．Journal of Southwest China Normal University（Natural Science），2012，37（11）：14－18．（王丽花，岳德权．带有小修和更换策略的多状态退化系统的可靠性分析［J］．西南师范大学学报（自然科学版），2012，37（11）：14－18．）

［17］Jia J S，Gao J L，Liu S F．Research on replacement model for regular overhauling repairable system［J］．Mathematics in Practice and Theory，2010，40（4）：114－119．（贾积身，高建来，刘思峰．定期检修可修系统更换模型研究［J］．数学的实践与认识，2010，40（4）：114－119．）

［18］Hu F，Deng S M．Optimal periodic preventive overhaul policy for degenerate production systems under a free－repair warranty［J］．Chinese Journal of Applied Probability and Statistics，2012，28（1）：63－78．

［19］Wang G J，Zhang Y L．A bivariate optimal replacement policy for a cold standby repairable system with preventive repair［J］．Applied Mathematics and Computation，2011，218（7）：3158－3165．

E－mail：peakxde＠163．com

宋建社（1954－），男，教授，博士，主要研究方向为系统工程、维修信息化。

E－mail：jssong＠pub．xaonline．com

江克侠（1979－），男，讲师，博士，主要研究方向为系统工程、量子光学。

E－mail：jiangkexia＠163．com

李 浩（1984－），男，讲师，博士研究生，主要研究方向为军事系统建模与优化决策。

E－mail：lihao＠163．com

杨颖涛（1980－），男，讲师，博士，主要研究方向为系统工程、故障诊断。

E－mail：yangyt＠163．com

Maintenance and replacement policy for a repairable multi－state system with regular preventive repairs

WU Wen－feng1，2，SONG Jian－she1，JIANG Ke－xia3，LI Hao2，YANG Ying－tao1
（1．The Second Artillery Engineering University，Xi’an 710025，China；2．Department of Management Science and Engineering，Officers College of Chinese Armed Police Force，Chengdu 610213，China；3．Department of Physics，Engineering University of Chinese Armed Police Force，Xi’an 710086，China）

To study a deteriorating repairable multi－state system with regular preventive repairs，a new maintenance and replacement policy is proposed．Assume that the component in the system has more than one failure states．The occurrence of a failure state of any one type is mutually exclusive and stochastic．The regular preventive repair is“as good as old”and the repair after the system failure is not“as good as new”．The system is not running during the period of the regular preventive repairs and the effective age of the system is not effected by the regular preventive repairs．The arrival of the effective age of the system is assumed to be mutually stochastic at the working state，the preventive repair state or the maintenance state．Under these assumptions，we consider a replacement policy Tbased on the effective age of the system．By using the generalized geometric process theory and the renewal process theory，the mathematic model is been established and the explicit expression of the long－run expected profit per unit time is derived．The optimal maintenance and replacement policy T＊can be calculated by the computer．Finally，we discuss the results of the model．This model can be used as references to the failure system maintenance and replacement．

geometric process；repairable system；preventive repair；multi－state system；replacement policy；expected profit

TB 114．3

A

10．3969／j．issn．1001－506X．2015．06．15

毋文峰（1978－），男，讲师，博士，主要研究方向为系统工程、可靠性维修工程。

1001－506X（2015）06－1319－06

2014－03－14；

2014－10－03；网络优先出版日期：2014－11－19。

网络优先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141119．2200．004．html

国家自然科学基金（61132008）资助课题