孤立波作用下排柱附近流动特性数值分析

蒋昌波，邓 涯，姚 宇，邓 斌

（1.长沙理工大学 水利工程学院，湖南 长沙410004；2.水沙科学与水灾害防治湖南省重点实验室，湖南 长沙410004）

海啸是一种破坏性极强的海洋灾害.海啸波首波达到近海岸时波高急剧增加，非线性特征增强，近似于孤立波，所以对海啸通常采用孤立波来模拟［1］.在海啸波向近岸推进过程中，水体内部蕴含着巨大的能量，会对近岸建筑物产生巨大冲击和潜在破坏［2］，海啸的危害在2004年印度洋海啸和2011年日本海啸中已经得到充分表现.因而对于海啸波与海洋建筑物相互作用的研究已经成为海啸灾害防治相关研究的热点.近年来随着海洋开发的不断拓深，多圆柱结构开始广泛应用于各种海洋和海岸工程建筑物，如海底管线、桩式防波堤、海洋钻井平台和跨海大桥的基础等.所以研究孤立波与多圆柱之间的作用机理，对于评估海啸波对这类建筑物的破坏作用具有十分重要的指导意义.

由于圆柱间水流结构的相互影响，多圆柱绕流问题相比传统的单圆柱绕流问题更为复杂.在孤立波与多圆柱相互作用过程中，自由液面变化剧烈，圆柱附近水体的非恒定特性和三维特征明显.目前国内外对此类问题的研究较少且以实验研究和数值模拟为主.Huang等［3］以排桩式防波堤为背景对孤立波与圆形排柱间的相互作用进行了物理模型实验研究，分析了排柱间隙大小与孤立波波高衰减之间的规律.Liu［4］在Huang［3］单排圆柱实验的基础上，对孤立波波高的衰减和排柱附近的流场进行了数值模拟研究.但由于受到浅水波方程的限制，该模型不适应于非线性较强的孤立波，也不能描述沿水深方向的流动特征.

基于Navier-Storks方程的OpenFOAM 作为CFD 开源程序包，以易扩展、并行计算稳定高效和求解方法先进等优点在计算流体力学领域得到了广泛的应用，近年来也开始应用于波浪与圆柱的相互作用问 题.Mo 等［5］和Lara 等［6］分 别 采 用Open-FOAM 开源程序包对孤立波与三圆柱间相互作用进行了数值模拟研究，分析了三圆柱附近的自由液面、流速、和动水压强的变化规律.但由于研究侧重点不同，Mo等［5］和Lara等［6］并没有分析多圆柱附近涡结构的发展和流场特性.国内对孤立波与圆柱间相互作用的数值模拟研究甚少，主要为规则波作用下的单个圆柱模型研究，如祝兵［7］和曹洪建［8］.

综上所述，为了弥补孤立波与排柱相互作用的研究中现有数值方法（如浅水波方程）的不足，分析排柱附近垂向上的水流结构，本文拟在Huang等［3］圆形排柱物理实验研究的基础上，利用OpenFOAM中的不可压缩气液两相流求解器interFoam 来建立三维数值波浪水槽，模拟孤立波与单排圆柱间的相互作用过程.通过计算分析排柱附近自由液面、平面／立面流线以及平面涡量场的变化来研究排柱附近的三维流动特性.

1 数值模型

1.1 控制方程

数值模型是求解连续不可压缩流体的气液两相流雷诺时均N-S 方程.自由面的捕捉是采用VOF方法，引入了流体体积分数φB，其值大小代表液体体积在计算网格中所占的比例，φB＝1 表示液体，φB＝0表示气体，介于0和1之间表示该网格为气液交界面，其输运方程如下：

式中：u为速度，ur为相对速度.该方法与经典VOF模型中的体积分数输运方程相比多了等式左边的最后一项，称为人工压缩项，其作用是使其对自由液面的捕捉更加精确.

气液两相流的动量方程中在方程右端增加了包含有体积分数的表面张力一项［9］，相应控制方程如下：

连续性方程：

动量方程：

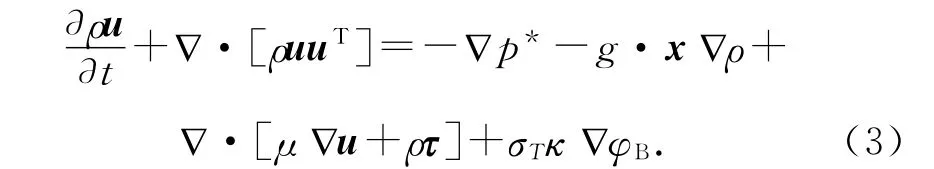
式中：u＝［u，v，w］是笛卡尔坐标系下流速场；p＊为动水压强；ρ为密度；g 为重力加速度；μ 为流体的动力黏度；ρ＝ρ（x）大小与计算网格内气液所占体积有关；τ为雷诺应力：

式 中：μt 为 湍流黏 度；k 为 紊 动 动 能；I为Kronecker张量；S 为应变速率（1／2（▽u＋（▽u）T））；▽为向量算子（∂／∂x，∂／∂y，∂／∂z）T；x＝（x，y，z）为Cartesian坐标系.式（3）右端最后一项σTκ ▽φB为表面张力，σT为表面张力系数，取值为0.074kg／s2；κ 为界面曲率，即

OpenFOAM 使用有限体积法对N-S方程进行离散，方程求解是采用PIMPLE 算法实现压力和速度的解耦，时间离散采用Euler格式，压力梯度离散采用Gauss线性离散格式，拉普拉斯项离散采用修正后Gauss线性离散格式，具体离散格式与过程详见文献［10］.

1.2 数值造波

1.2.1 造波和消波方法 采用Jacobsen［11］提出的修正速度入口方法进行造波.与通常的速度入口造波方法不同，该方法中造波边界的类型分为干网格、湿网格和临界网格3种，其中干网格的边界条件为

式中：n为边界网格面的单位法向向量.湿网格边界条件（u和φB）是根据相应的波浪理论计算所得.模型对临界网格进行了湿面修正.波浪理论计算的自由液面曲线与网格边界存在2个交点，取两点相连直线作为临界网格的湿面边界，得到网格湿面部分的中心位置，以此计算出临界网格的入流速度和体积分数.对临界网格的处理，避免了入口处自由液面的虚拟振荡.

消波方法采用松弛因子法，对消波区网格的计算变量φ（u和φB）进行数值修正：

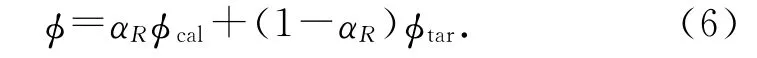
式中：αR为松弛因子，消波区域和非消波区域交界面上αR＝1，在消波区域αR∈（0，1），φcal为变量的计算值，φtar为变量的消减目标值.

1.2.2 造波验证 本文对数值波浪水槽进行了孤立波造波和传播的验证.验证水槽长11 m、高0.3m，宽为一个网格大小，两端设置长1m 的数值消波区（Relexation Zone）.模拟水深0.15 m，孤立波波高0.07m，造波起点设在x＝3m 位置（x＝0为计算左端边界），计算网格大小为0.01m，时间步长为自适应调整步长，验证结果如图1所示.孤立波波面和流速理论公式为

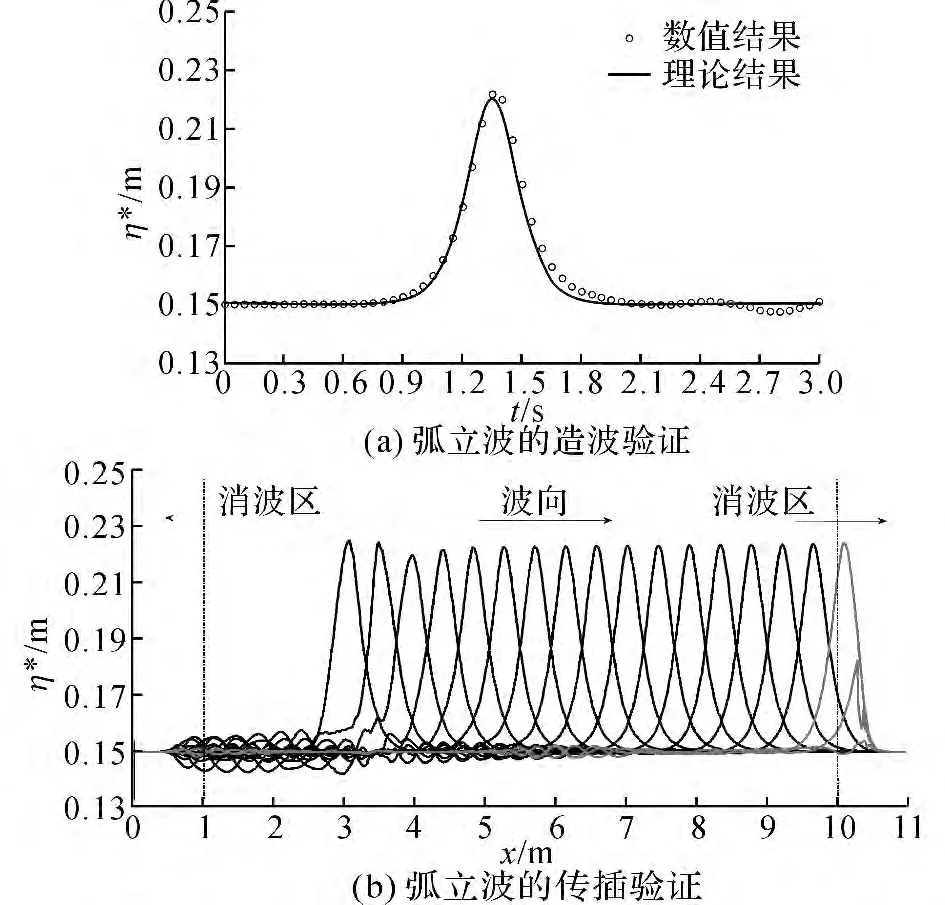
图1 孤立波造波验证Fig.1 Verification of solitary wave generation and propagation

式 中：η 为 自 由 液 面 变 化 值，H 为 波 高，h 为 水 深，c为波速.

如图1（a）所示数值生成的孤立波波形与理论波形一致，其中η＊为自由液面高程值，数值计算的波面历时数据取自数值造波点后3m 处（x＝6m）.孤立波在传播过程中，除造波点后2m 区域内（x＝3～5m）波高有略微振荡外，在其他区域波高基本保持不变，水槽两端的消波效果良好（图1（b）中灰实线所示）.通过对数值模拟的相邻时刻孤立波水平传播距离进行分析，得到孤立波的传播速度ccal＝1.43m／s，根据式（8）计算理论波速为ctho＝1.47 m／s，两者较为符合（误差小于3%）.因而该模型可以有效的模拟孤立波的生成和传播过程.

2 模型设置与验证

为了验证数值模型能否合理地模拟孤立波与排柱相互作用的过程，数值模型的设置与Huang等［2］的物理模型实验一致，其模型设置如图2（a）所示，以孤立波传播方向为x 方向，水槽断面方向为y 方向，水深方向为z方向建立空间直角坐标系，原点位于入口端水槽边壁的底部位置.水槽宽0.54 m，排柱模型直径d＝0.03 m，相邻圆柱圆心间距S＝0.045m，在x＝8m 处沿水槽横断面方向对称布置12根，在排柱模型前3m 和后1.5m 位置分别布置有浪高仪G1、G2.

图2 数值水槽和排柱附近网格划分Fig.2 Wave numerical tank and computational grids around cylinders

为节省计算资源，数值计算域选定水槽中间宽0.27m 的区域，包含有6根圆柱.上下选用对称边界以消除边壁效应的影响，最外层圆柱圆心距边界距离为S／2，如图2（a）阴影区域所示.数值水槽在长度和高度方向的设置与图1（b）所示相似，造波起点位于排柱前5m 位置，水槽入口端和出口端设置有长为1m 的数值消波区.同时为了保证排柱前后入射波和透射波的稳定传播，排柱前后分别设置有5和2m的富余长度，总计算区域长为11m.数值水槽的计算网格采用分区多块结构网格.计算区域中y 和z 方向网格大小相等dy＝dz＝0.006m，x 方向网格大小则是分区设置.在排柱前1m 至后0.5m区域内，x 方向网格大小为dx＝0.006m，在造波起点和排柱后2m 位置点dx＝0.01m，在入口和出口位置点dx＝0.02m，相邻位置点间网格进行均匀过渡.在水槽网格的基础上，排柱附近网格采用snappyHexMesh工具［12］进行划分：对圆柱表面采用单层贴体网格，排柱附近由加密的结构网格填充，与外层结构网格的衔接则是采用三角棱柱非结构网格（如图2（b）所示），网格总数为2 908 350.进一步加密圆柱附近的网格后计算结果改进不明显，说明排柱附近的网格设置可以满足计算要求.同时本文进行了单柱模型的对比模拟，单柱附近网格生成方法与排柱情况相同，网格总数为2 839 600.

本文选用一个典型的实验工况（水深h＝0.15 m，孤立波波高H＝0.07m）进行研究，湍流模型采用文献［11］建议的SSTk-ω 模型，时间步长为自适应时间步长，计算时长为8s，以保证反射波传至G1测点.

本模型中具体的边界条件设置为：水槽两侧为对称边界，底部和圆柱表面为固壁无滑移边界，上方空气为自由进出流边界，其中空气区域高0.15 m，以防止水流溢出.

图3 自由液面历时曲线的数值计算和实验结果对比Fig.3 Comparison between numerical and experimental time series of free surface elevation0.86，Kd＝0.50，实验和数值结果符合较好.

3 结果分析与讨论

3.1 自由液面的变化

图4 不同时刻的自由液面Fig.4 Free surfaces at different time steps

图5 各个圆柱附近的自由液面变化Fig.5 Surface elevations around cylinders

与传统的沿水深积分的二维数值波浪模型（如浅水波方程）相比，该模型能更合理的模拟排柱附自由液面的三维特性：图5表明单个圆柱表面自由液面壅高沿中轴线（θ＝π）两侧近似对称分布.在柱前位置（θ＝π）壅高达到最大，自由液面变化相对值为1.7，在柱后附近位置（θ＝π／8（15π／8））达到最小，自由液面变化相对值为0.6，两者差值的相对值为1.1.在θ＝π到θ＝π／2（3π／2）位置，壅高逐渐减小，液面变化相对值为0.1.在θ＝π／2（3π／2）到θ＝π／4（7π／4）位置，壅高出现了急剧下降，液面变化相对值0.6.在θ＜π／4，θ＞7π／4范围内，壅高变化幅度较小.

3.2 平面和立面流线特征

孤立波与排柱相互作用过程中，水流结构复杂多变，三维特征明显.故本文分别选取z／h＝0.83位置x-y 平面（平面的选取保证其始终位于自由液面以下，并且尽可能接近静水面位置z／h＝1）和y／d＝9位置x-z 立面（立面的选取位于圆柱3和圆柱4的间隙中心线上）为例，来研究排柱附近水流的三维流线特征，如图6 所示为不同时刻排柱附近的流线.图6中（a）～（e）为不同时刻的平面流线图，（f）～（i）为不同时刻的立面流线图，平面和立面位置如图中点画线所示.

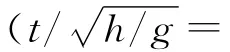
3.3 水平涡量场分析

排柱结构除了利用桩柱自身的反射外，还依靠排柱间隙产生的高速水流和柱后的尾涡脱落来增强入射波波能的耗散.为研究排柱附近自由液面涡动强度的变化规律，本文选取z／h＝0.83 位置的x-y平面（与3.2节一致）作为研究对象.由于各个圆柱附近水流结构相似，为了清晰展示排柱附近的流场结构和涡量特征，文中仅选取中间3根圆柱附近的区域作为研究对象，并且与相同孤立波作用下单柱的情况进行了比较，如图7所示.

图6 平面（z／h＝0.83）和立面（y／d＝9）不同时刻流线Fig.6 Streamlines on the horizontal（z／h＝0.83）and the vertical（y／d ＝9）planes of at different time steps

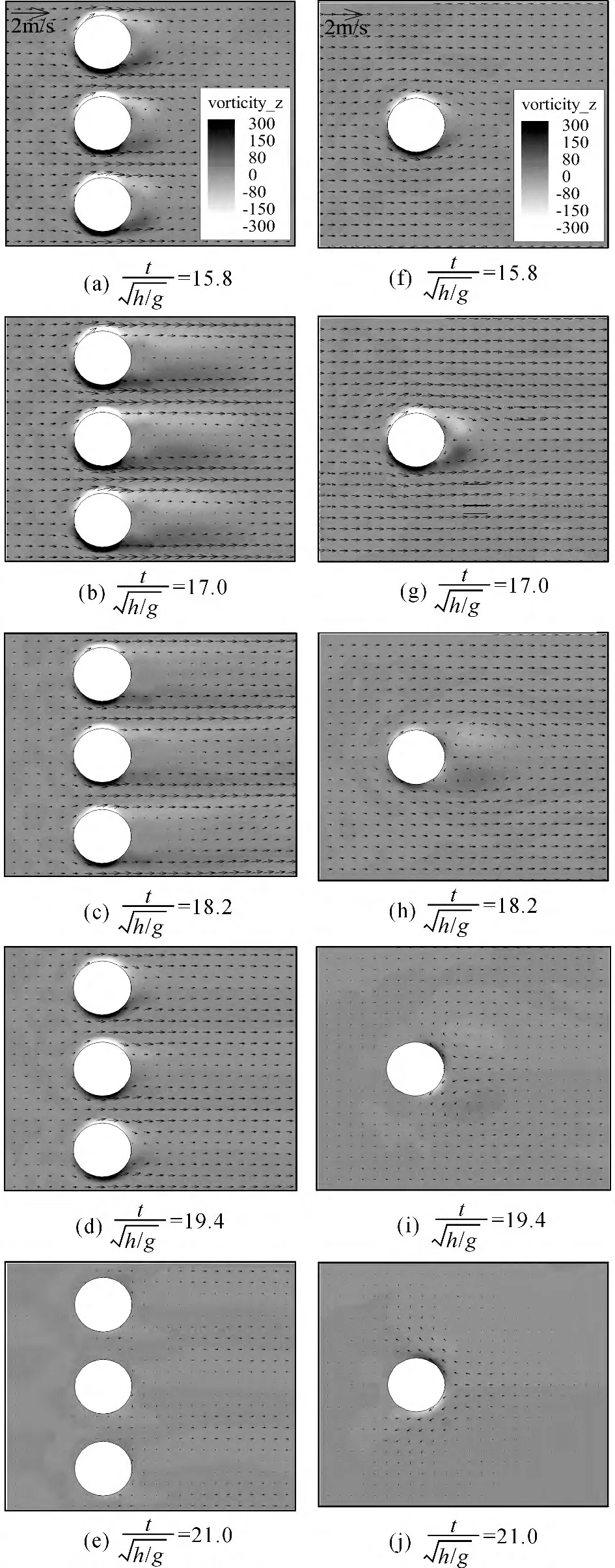
图7 z／h＝0.83位置平面上涡量（s-1）Fig.7 Vorticity on plane of z／h＝0.83（s-1）

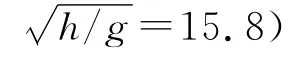
4 结 语

本文利用OpenFOAM 开源程序包建立三维数值波浪水槽，研究了孤立波与排柱相互作用下排柱附近流动特性的演变规律.圆柱表面边界层网格与外层结构网格采用了三角棱柱网格进行衔接.与传统的二维数值波浪模型相比，该模型能更合理的模拟排柱附近波浪传播的三维特性.研究结果表明：孤立波穿过排柱时，自由液面显著壅高，并沿柱面呈三维分布，随后在排柱前后分别形成沿上游传播的反射波和沿下游传播的透射波.排柱中各圆柱附近流动特性相似，柱前壅高最大时柱间水体以水平运动为主，垂向流速较小，具有典型的浅水长波流动特征；圆柱下游形成对称分布的漩涡，并逐渐耗散消失.与孤立波作用下单柱附近的涡量特征相比，排柱后方涡动强度较大，且尾涡的发展纵向相对伸长、横向相对收缩.本文的研究成果将为进一步分析排柱的受力特征以及排柱附近的泥沙运动规律提供参考.

（

）：

［1］CHANG Y H，HWANG K S，HWUNG H H.Largescale laboratory measurements of solitary wave inundation on a 1：20slope［J］.Coastal Engineering，2009，56（10）：1022-1034.

［2］陈杰，蒋昌波，邓斌，等.海啸作用下岸滩演变与床沙组成变化研究综述［J］.水科学进展，2013：750-758.CHEN Jie，JIANG Chang-bo，DENG Bin，et al.Review of beach profile changes and sorting of sand grains by tsunami waves ［J］.Advances in Water Science，2013，24（5）：750-758.

［3］HUANG Z，YUAN Z.Transmission of solitary waves through slotted barriers：A laboratory study with analysis by a long wave approximation［J］.Journal of Hydro-Environment Research，2010，3（4）：179-185.

［4］LIU H，GHIDAOUI M S，HUANG Z，et al.Numerical investigation of the interactions between solitary waves and pile breakwaters using BGK-based methods［J］.Computers ＆ Mathematics with Applications，2011，61（12）：3668-3677.

［5］MO W，LIU P L F.Three dimensional numerical simulations for non-breaking solitary wave interacting with a group of slender vertical cylinders［J］.International Journal of Naval Architecture and Ocean Engineering，2009，1（1）：20-28.

［6］LARA J L，HIGUERA P，GUANCHE R，et al.Wave interaction with piled structures：application with IHFOAM［C］∥ASME 2013 32nd International Conference on Ocean，Offshore and Arctic Engineering.Nantes，France：American Society of Mechanical Engineers，2013：V007T08A078.

［7］祝兵，宋随弟，谭长建.三维波浪作用下大直径圆柱绕流的数值模拟［J］.西南交通大学学报，2012，47（2）：224-229.ZHU Bing，SONG Sui-di，TAN Chang-jian.Numerical simulation for diffraction around large-diameter circular cylinder subjected to three-dimension wave［J］.Journal of Southwest Jiao Tong University，2012，47（2）：224-229.

［8］CAO H J，ZHA J J，WAN D.Numerical simulation of wave run-up around a vertical cylinder［C］∥Proceedings of the 21st International Offshore and Polar Engineering Conference.Maui，Hawaii，USA：International Society of Offshore and Polar Engineers，2011：726.

［9］RUSCHE H.Computational fluid dynamics of dispersed two-phase flows at high phase fractions［D］.London，UK：University of London，2002.

［10］Open CFD.OpenFOAM User Guide，Version 2.2.1［EB／OL］.2013-10-20.http：∥www.openfoam.com／.

［11］JACOBSEN N G，FUHRMAN D R，Fredsøe J.A wave generation toolbox for the open‐source CFD library：OpenFoam［J］.International Journal for Numerical Methods in Fluids，2012，70（9）：1073-1088.

［12］JACKSON A.A comprehensive tour of snappyhexmesh［R］.Darmstadt，Germany：The 7th Open-FOAM Workshop，2012.