大型异构多子以太网物理拓扑发现算法研究*

马晓波，杨国林

（内蒙古工业大学信息工程学院，呼和浩特010080）

大型异构多子以太网物理拓扑发现算法研究*

马晓波，杨国林

（内蒙古工业大学信息工程学院，呼和浩特010080）

正确的网络物理拓扑信息对许多网络管理任务起着至关重要的作用，而实际网络中可能存在不易被发现的“哑”设备，这给网络拓扑发现带来了很大难度，传统的拓扑发现算法不能全面发现网络设备。针对这种情况，提出一个大型的异构多子以太网物理拓扑发现算法。算法首先利用通用的MIB信息，得到任意两个节点间的直接连接，然后选择具有最小可能连接数的节点，使用扩展规则使所有的RSs完整。实验结果表明，不需要修改任何硬件或软件资源，能够发现“哑”设备，保证拓扑发现与给定输入库兼容。该算法在地址转发表不完整的情况下，能够高效、全面、正确地发现网络的物理拓扑结构。

异构多子网；物理拓扑发现；哑设备；地址转发表

1 引 言

很多网络管理任务（如性能分析、故障识别等）取决于网络连接知识。然而，目前网络工具不能让网络管理员得到精确的网络设备连接图，没有高性能的工具来定位网络故障、调整网络性能或识别网络流量的瓶颈，获取数据链路层（ISO体系的第二层）的网络拓扑信息十分困难，市场上的商业网络管理平台不能自动地发现网络拓扑结构。目前市场上的商业工具（例如：HP’s OpenView（opeview.hp.com），IBM’s Tivoli（tivoli.com），Cisco’s Discovery Protocol（www.cisco.com），and Nortel’s DiscoveryProtocol（www.nortelnetworks.com））大多数基于私有信息，而且在大型的多子以太网中往往无法全面捕捉第二层的连接关系，如果网络中有哑设备（hubs或semihubs），拓扑发现会变得更加复杂。许多物理网络拓扑发现算法使用本地节点的网桥和IP MIB信息。然而，网桥和交换机只参与有限的信息交换，在生成树协议期间，它们只与它们的邻居节点通信，相关的MIB信息被存储在地址转发表（Address Forwarding Table，AFT）中。

在研究了含哑设备（hubs或semihubs）的大型异构多子以太网物理拓扑发现存在的问题后，提出了一个新的实用的物理拓扑发现算法，该算法只利用通用的MIB信息，不需要修改任何硬件或软件资源，能够全面发现网络设备的连接情况，时间复杂度为O（n3），较以前算法有很大改进。

2 相关工作

文献［1］提出了不含哑设备的多子网物理拓扑发现算法，但要求地址转发表完整，而且多数情况下得到的网络拓扑结构不唯一。文献［2］中提出的多子网物理拓扑发现算法能够发现“哑”设备，然而，在地址转发表不精准的情况下，不能发现正确的网络拓扑。文献［3］中Lowekamp等人提出的算法可以在地址转发表不完整的情况下发现网络拓扑，也能发现hubs，但是该算法适用于单子网，在多子网情况下非常容易出错。为了在地址转发表不完整的情况下发现多子网的物理拓扑，文献［4］中提出了一个“两阶段”方法：第一阶段，他们试图利用地址转发表的扩展规则使不完整的地址转发表完整，如果能够使地址转发表完整，则进入第二阶段，即使用文献［1］中提出的算法来发现网络设备的连接情况，然而，要使不完整的地址转发表完整非常困难，甚至有时实现不了。文献［5］中给出了一种基于生成树协议的物理拓扑发现算法，然而，不像网桥信息，大多数的网络供应商不会定期提供生成树的根信息。

3 网络模型

进行拓扑发现的网络区域称为交换域，交换域中的节点使用生成树协议确定节点之间唯一的转发路径。可以将网络中的节点分成三类：①在拓扑发现过程中访问过该节点的MIB；②在拓扑发现过程中没有访问过该节点的MIB，但该节点出现在了第一类节点的MIB中；③在拓扑发现过程中没有访问过该节点的MIB，且该节点也没出现在其它节点的MIB中。第二类和第三类节点称为哑设备（hubs或semihubs），当semihubs或hubs直接相连时，拓扑发现很难发现它们以及它们之间的连接情况。

网络模型用无向树N＝＜V，E＞来表示，其中V是网络节点集合，E是节点之间的物理连接集合。对于网络N中的节点a来说，如果它不是hub，则用p（a）表示节点a的端口数，用ai表示节点a的第i个端口，用subnet（a）表示节点a所属的子网。如果节点a是终端节点当且仅当p（a）＝1。中间节点（即非叶子节点）代表第二层网络元素（交换机和网桥）。同一交换区域中的数据包从一个节点转发到另一个节点不需要经过路由器，然而，对于不同子网的网络设备之间要想通信必须经过各自子网的路由器。因此，把路由器看作主机，路由器和主机表示为终端节点（即叶子节点）。

如果节点a和b通过端口ai和bj相连，当且仅当在节点a和b间有从端口ai到端口bj的路径存在。路径上边的数目称为路径长度，如果路径长度为1，那么端口ai和bj直接相连。

端口ai的地址转发表记为AFT（ai），满足下列性质：①如果subnet（bj）＝subnet（ai）且从ai到bj有路径存在，则bj∈AFT（ai）；②如果subnet（bj）≠subnet（ai），但是有端口ck满足subnet（ck）＝subnet（ai）并且有路径ck…bj…ai存在，则bj∈AFT（ai）。这就意味着，AFT（ai）中包含在端口ai上收到的所有数据包的目的地址。当节点a收到数据包时，如果AFT（ai）中包含此数据包的目的地址，则节点a会通过端口ai转发此数据包。如果AFT（ai）中包含端口ai上收到的所有数据包的目的地址，不包含从ai到达不了的节点，则称AFT（ai）是完整的。除了端口ai外，在节点a的其它端口上看到的节点集合称为AFT（ai）的补集，记为CAFT（ai）。因为网络用树来表示，且任何节点都不能在它自己的端口上看见它自己，所以a∈CAFT（ai）。

如果端口ai和bj之间有路径存在，那么CAFT（ai）∩CAFT（bj）＝Ø。因为如若不然，则至少存在一个节点c，能通过两条不同的路径到达c：一条来自于端口ak（k≠i）；另一条来自于端口bl（l≠j）。因此，如果CAFT（ai）∩CAFT（bj）≠Ø，则端口ai和bj之间没有路径存在。如果端口ai和bj直接相连，则AFT（ai）∩AFT（bj）＝Ø。

从端口ai可到达的节点集合记为RS（ai）。通过定义可知，a不属于RS（ai）。如果a是终端节点（也就是说a只有一个端口），那么RS（a1）包含除a外的所有网络节点。RS（ai）的补集记为CRS（ai），即CRS（ai）＝V－RS（ai）。在单子网中，如果地址转发表是完整的，则RS（ai）＝AFT（ai）。然而，在多子网中，节点a的MIB中不包含RS（ai）信息，但包含AFT（ai）信息。用图1（a）进一步说明AFT、CAFT、RS和CRS的概念，图1中节点x是semihub，黑圈是hub，有两个子网：s1＝｛1，2，x｝，s2＝｛3，4｝，表1列出了AFTs、CAFTs、RSs和CRSs的值。

图1 含semihub和hub的网络和PDCG

表1 图1（a）中各端口的AFT、CAFT、RS和CRS值

为了推出端口ai和bj直接连接，下面介绍可能直接连接（Potential Direct Connection，PDC）的概念：

（1）AFT（ai）∩AFT（bj）＝Ø

（2）AFT（ai）∪AFT（bj）是一组子网

（3）CAFT（ai）∩CAFT（bj）＝Ø

（4）如果ai和bj属于同一子网，那么没有满足下面条件的ck存在：ck与ai不在同一子网；AFT（ai）∪AFT（bj）＝AFT（ai）∪AFT（ck）；其中AFT（ai）和AFT（ck）满足上面三个条件。

由上面可得出直接连接是PDC的子集。端口ai和bj可能连接（Potential Connection，PC）当且仅当CRS（ai）∩CRS（bj）＝Ø。PDCG（Potential Direct Connection Graph）是可能直接连接图，端口作为PDCG的节点，如果端口ai和bj可能直接连接则在PDCG中它们之间有边存在。例如，在图1（a）中，端口b2和2间有一个PDC，PCs为（a2，b1）和（a1，b2），图1（a）的PDCG如图1（b）所示。

4 拓扑发现算法

4.1 RS的扩展过程

规则1：如果端口ai和bj相连，a≠b，那么RS（ai）＝RS（ai）∪CRS（bj）且RS（bj）＝RS（bj）∪CRS（ai）。

规则2：如果端口ai和bj相连，a≠b，子网su中有一节点c，c∈RS（ak）（k≠i），并且对任何端口bl，RS（bl）不包含子网su中的节点，那么RS（bj）＝RS（bj）∪C（C包含子网su中的所有节点以及从子网su中能看到的节点）

证明：用反证法证明。因为网络拓扑是一棵树，所以网络中的任意两个节点之间只有一条路径。假设子网su中有两个节点c和d（c≠d），c∈RS（ak），d∈RS（aq），且在子网su中没有属于RS（bl）的节点（l是节点b的任意端口）。假设把节点c和d分别加到RS（bj）和RS（bk）中，但是，因为端口ai和bj相连，所以节点d也一定出现在RS（bj）中，矛盾。定理得证。

见图1（a），因为在PDCG中有边＜b2，2＞，所以b2和终端节点2直接连接。因此，节点a和b间唯一的可能连接变成了连接。应用规则2可得出RS（b1）包含节点1、3、4、x和a，RS（a2）包含节点2、4和b（见表1）。

4.2 算法描述

该算法分两个阶段：第一阶段，发现MIB中任意两个节点间的直接连接；第二阶段，选择两个它们之间具有最小可能连接数的节点，这个连接数不可能大于2（证明见下4.3）。选择了可能连接后，使用扩展规则扩展RSs，重复这个过程直到所有的RSs是完整的。每一阶段都需验证CRS的交集是否为空，该算法的时间复杂度为O（n3）。算法描述如下所示。

Input：A set of complete AFTs

Output：A set M⊆PDC ofmatchings

uniqueness＝unique；

Phase＃1

Generate Potential Direct Connection Graph PDCG（N）；

M＝Ø；CC＝（｛a｝，…，｛c｝）where CC is the set of connected components each of which at this stage is a single node；

Do while（PDCG（N）is not empty）

1.If there is a terminal node aiin PDCG（N）and U（ai，bj）is an edge in PDCG（N），

select U（ai，bj）；

（a）M＝M∪｛（AFT（ai），AFT（bj））｝；

（b）If a∈CCland b∈CCkand k≠l，thenCCl＝CCl∪CCk；delete CCkfrom CC；

（c）remove from PDC（N）Graph all edges，whose endpoints are in CCl；

2.If there are no terminal nodes in PDCG（N），uniqueness＝not unique；

（a）select an arbitrary PDC（ai，bj）；

（b）Goto 1a；

Phase＃2

Generate PCs as follows：

for any two ports aiand bjdo if CRS（ai）∩CRS（bj）＝Ф，then add＜ai，bj＞to PCs；

Do while（set of PCs is not empty）

1.find two nodes a and b such that the number of potential connections between a and b in the set of PC isminimal；

2.if＜ai，bj＞is notunique potential connection，uniqueness＝not unique；

3.M＝M∪｛（RS（ai），RS（bj））｝；（break ties arbitrarily）

4.Delete＜ai，bj＞from further considerations；

5.oldRS（ai）＝RS（ai）；

6.oldRS（bj）＝RS（bj）；

7.Extend RS（ai）and RS（bj）；

8.oldRS（ai）＝RS（ai）；

9.oldRS（bj）＝RS（bj）；

10.Update the set of PCs；

Return M and uniqueness；

4.3 正确性证明

接下来证明利用该算法得到的拓扑与输入的AFTs兼容。首先证明至少有两个节点a和b，它们之间的可能连接数不大于2。接下来证明在节点a和b间有两条可能连接或没有可能连接的情况下，如何选择节点a和b间的可能连接生成正确的拓扑。

定理1：如果AFT（ai）∩AFT（bj）≠Ø，i、j分别是节点a、b的端口，那么节点a和b间至多有两条可能连接。

证明：假设有一节点u，u∈AFT（ai）∩AFT（bj），且u属于子网s，因为没有AFT会包含同一子网中所有的节点，所以可设有一节点v，v属于子网s，并且v∈AFT（ak），v∈AFT（bl），i≠k，j≠l。考虑下面两种情况：

（1）子网s中的所有节点至少出现在节点a或b的三个端口上。假设图2（a）中的端口ai和bj间有路径，并设子网s中的节点u、v和w，u∈AFT（ai），v∈AFT（ak），w∈AFT（am）。因为拓扑图用树表示，所以节点v和w一定属于AFT（bj）。又因为节点u属于子网s，所以它一定出现在节点a和b的AFTs中。假设u∈AFT（bl）和u∈AFT（ai），则｛v，w｝∈CAFT（ai）∩CAFT（bL），u∈CAFT（bj）∩CAFT（ap），p≠i，且｛u，v，w｝∈CAFT（ap）∩CAFT（bq），p≠i≠k≠m，j≠l≠q。因此，（ak，bj）是节点a和b间唯一的可能连接。

（2）子网s中的所有节点至多出现在节点u和v的两个端口上。假设子网s中的所有节点出现在节点a和b的AFTs中，在图2（b）中，对节点a的AFT（ai）和AFT（ak）、节点b的AFT（bj）和AFT（bl）有u∈AFT（ai）∩AFT（bj），v∈AFT（ak）∩AFT（bl）。因此，在节点a和b间只有两条可能连接：（ak，bj）和（ai，bl），这是因为u∈CAFT（ak）∩CAFT（bp），p≠l，v∈CAFT（bj）∩CAFT（aq），q≠k。

图2 为了定理1的证明

定理2：如果RS（ai）∩RS（bj）≠Ø，i、j分别是节点a、b的端口，AFT（ap）∩AFT（bq）＝Ø（p、q分别是节点a、b的任意端口），那么（ai，bj）是节点a和b间唯一的可能连接。

为了说明这种情况见图3（a），节点u和v属于子网s1，节点p和q属于子网s2。

证明：假设有一子网s1，u是子网s1的节点，u∈RS（ai）∩RS（bj），子网s1属于节点a和b的某一端口，在扩展过程中s1一定被加到RS（ai）和RS（bj）中。因此，有一节点c，使路径（cp，ai）和（cq，bj）存在，节点c或者属于子网s1或者节点c至少从两个端口上能看见子网s1中的节点，而且，子网s2中的节点u和v、子网s3中的节点w和z和子网s2中的节点能被节点a和c的AFTs看到，子网s3中的节点能被节点b和c的AFTs看到。如果节点a在节点c和b间的路径上，如图3（b）所示，那么节点u和v能被节点a的两个AFTs看见，因此，这与假设（节点a和b的AFTs交集为空）矛盾。如果节点c在节点a和b间的路径上，那么有下列情况存在：

图3 为了定理2的证明

（1）节点c通过端口cp和cq（p≠q）分别与节点a和b相连，如图3（c）所示；

（2）节点c通过端口cp与节点a和b相连，如图3（d）所示。

首先考虑第一种情况。当选择可能连接（ai，cp）进行扩展时，应用规则2，子网s1和s2中的所有节点和从子网s1和s2中能看到的所有节点被加到RS（ai）中，因此子网s1中的所有节点和节点u、v、b被加到RS（ai）中。同样，当选择连接（cq，bj）进行扩展时，子网s1中的所有节点和节点w、z、a被加到RS（bj）中。因为a∈RS（bj）且b∈RS（ai），所以节点a和b间存在唯一的可能连接。

使用同样的方法，第二种情况的正确性也能被证明。

定理3：如果节点a和b间不存在唯一的可能连接，a≠b，那么没有这样的节点u和v使｛u，v｝∈AFT（ai），u∈AFT（bj），v∈AFT（bk），j≠k。

证明：假设网络中有两对不同的节点a、b和u、v，且｛u，v｝∈AFT（ai），u∈AFT（bj），v∈AFT（bk），j≠k，如图4（a）所示。因为每个节点要么能看到同一子网中的所有节点要么一个也看不到，所以有一节点w，节点u、v和w属于同一子网，且w∈AFT（bk）。因此，下面的关系成立：w∈CAFT（ai）∩CAFT（by），y≠k，u∈CAFT（ax）∩CAFT（bk），x≠i，v∈CAFT（ax）∩CAFT（by），x≠i，y≠k。所以，连接（ai，bk）是唯一的。

定理4：如果网络中任两个节点间没有唯一的可能连接，并且节点a和b间至多有两条可能连接，那么选择其中的一条可能连接来生成的网络拓扑与给定的AFTs集合兼容。

证明：假设端口b1与AFT（b1）中的节点不直接相连，如图4（b）所示，下面证明将端口b1与AFT（b1）中的节点相连可得到有效的网络拓扑。

从定理3可知，或者AFT（bi）∩AFT（cj）＝Ø（i、j分别是节点b、c的任意端口），或者AFT（ak）∩AFT（cj）＝Ø（k、j分别是节点a、c的任意端口），因此，考虑下面情况：

（1）AFT（bi）∩AFT（cj）＝Ø（i、j分别是节点b、c的任意端口），在这种情况下，AFT（b1）⊂AFT（a1）。设F＝AFT（a1）∩AFT（b1）。因为在节点a和b间恰有两条可能连接（根据定理1），所以将端口b1与F中的节点相连可在端口b2和a1间得到一条唯一的连接。通过扩展节点a和b的AFTs，节点c、11、21和从这些节点能看到的节点会被加到AFT（b2）中。最后，如果将端口b2连到端口d1上，那么（a2，d1）是一个有效的可能连接（因为a2和d1间有路径）。

?图4 为了定理3和定理4的证明

（2）AFT（ai）∩AFT（cj）＝Ø（i、j分别是节点a、c的任意端口），在这种情况下，AFT（a1）⊂AFT（b1）。设F＝AFT（a1）∩AFT（b1）。因为在节点a和b间恰有两条可能连接，所以将端口b1与F中的节点相连可在端口b2和a1间得到一条唯一的连接。通过扩展节点a和b的AFTs，将得到如图4（c）所示的拓扑。

5 综合实例

这里介绍两个实例。第一个实例证明算法利用AFTs可唯一的确定网络拓扑结构；第二个实例证明算法利用AFTs虽不能唯一的确定网络拓扑结构，但能发现网络的所有拓扑结构。

图5 含hub的网络模型

见图5所示的网络：黑圈代表hubs，子网有：s1＝｛s，t｝，s2＝｛x，y｝，s3＝｛u，v｝，s4＝｛r，q｝，节点a，b，c，d和e的AFTs见表2。

表2 多子网图5中各端口的AFT值

端口e2、x间和端口e3、u间有一个PDC，所以这些直接连接能被发现。应用算法的第一阶段和第二阶段可得到下列的PC组：（a1，b2），（a2，b1），（a1，c2），（a2，c1），（a1，d2），（a2，d1），（a1，e1），（a2，e1），（b1，c2），（b2，c1），（b1，d2），（b2，d1），（b1，e1），（c1，d2），（c2，d1），（c1，e1），（d1，e1）。

唯一的可能连接如下：（b1，e1），（c1，e1）和（d1，e1）。接下来扩展RS（b1）、RS（c1）、RS（d1）和RS（e1）。利用扩展规则1，节点e被加到RS（b1）中，节点b，q，t，v，y被加到RS（e1）中。因为从节点e的任何端口都看不到子网s4中的节点q和r，但在节点b的AFTs能看到节点q和r，利用扩展规则2，子网s4中的所有节点和从子网s4中能看到的节点都被加到RS（e1），因此节点q，r和a被加到RS（e1）。同理，扩展RS（e1）和RS（c1），节点e被加到RS（c1）中，节点c、s和t被加到RS（e1）中。最后，扩展RS（d1）和RS（e1）。各端口的RSs见表3。

之后得到的唯一可能连接是（b2，d1）和（c2，d1），扩展后的结果如表4所示。

下一步得到的唯一可能连接是（a2，d1），扩展后的结果如表5所示。

在这一阶段，每两个节点间有一个唯一的PC，所以可获得完整的RSs并能得到唯一的网络拓扑。

表3 发现了PC（b1，e1），（c1，e1）和（d1，e1）后得到的RS值

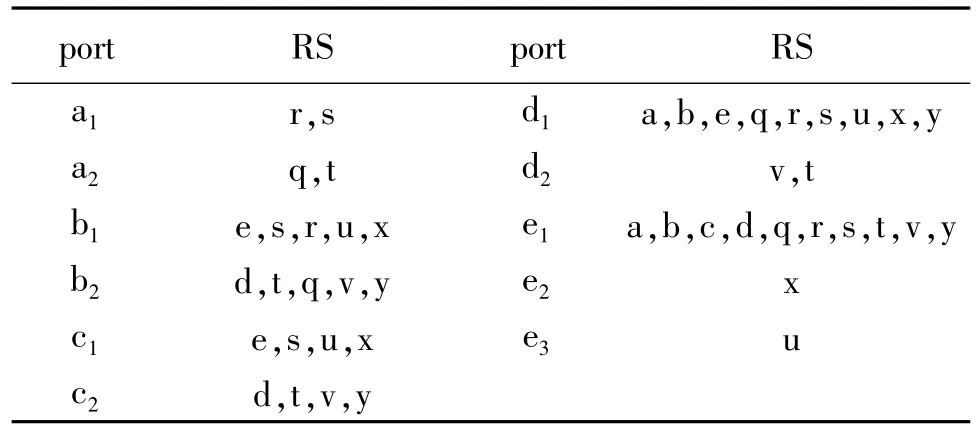
表4 发现了PC（b2，d1）和（c2，d1）后得到的RS值

表5 发现了PC（a2，d1）后得到的RS值

6 结束语

精准的网络拓扑发现对网络各方面的管理起着非常重要的作用。对现有的物理拓扑发现算法进行分析后，提出了一种异构多子以太网物理拓扑发现算法，克服了网络协议不一致，网络设备异构等带来的困难，在不完整的地址转发表情况下能够全面、准确、高效地发现大型网络的设备，该算法具有广泛的适用性。对于含VLAN的网络，只有在极少数私家Bridge－MIB中提供了相关信息，因此含VLAN的拓扑发现算法将是下一步研究工作的重点。

［1］ Breitbart Y，Garofalakis M，Jai B.Topology Discovery in Heterogeneous IP Networks：The NetInventory System［J］.IEEE/ACM Trans.Networking，2004，12（3）：401－414.

［2］ Y Bejerano，Y Breitbart，M Garofalakis，R Rastogi，Physical Topology Discovery for Large Multi－Subnet Networks［C］.In：Proceedings of INFOCOM 2003：342－352.

［3］ Lowekamp，David R.O’Hallaron，Thomas R Gross.Topology discovery for large ethenet networks［C］.In：Proceeding of ACM SIGCOMM，California，Aug 2001：237－248.

［4］ Y Sun，ZWu，Z Shi.The Physical Topology Discovery for Switched Ethernet Base on Connection Reasoning［C］.In：Proceedings of ISCIT，2005：42－45.

［5］ Y Sun，Z Shi，ZWu，A Discovery Algorithm for Physical Topology in Switched Networks［C］.In：Proceedings of the IEEE Conference on Local Computer Networks，2005： 311－317.

［6］ 马晓波.异构多子网的以太网物理拓扑发现算法研究［J］.计算机工程与科学，2008，30（9）：11－14.

［7］ 马晓波，杨国林，马志强，庄旭菲.异构IP网络物理拓扑发现的改进算法［J］.微处理机，2011，32（1）：18－20.

［8］ Xiaobo Ma，Guolin Yang，Xufei Zhuang.Research and Implementation on Algorithm of Automatic Physical Topology Discovery in Heterogeneous Multi－subnet［J］.Information Technology Journal，2013，12（20）：5736－5740.

Study on Algorithm of Discovering Physical Network Topology for Large Heterogeneous Multi－Subnet Ethernet Networks

Ma Xiaobo，Yang Guolin
（College of Information Engineering，Inner Mongolia University of Technology，Hohhot010080，China）

The exact network topology information is very important for many network management tasks，and some＂dumb＂devicesmay be not found in the network，so it is very difficult to conduct the network topology discovery because the classical topology discovery algorithm can not fully discover network devices.For this situation，a physical topology discovery algorithm of large heterogeneousmultisubnet ethernet networks is presented in this paper.Firstly，it discovers all direct connections between any two MIB－enabled nodes by the general information of MIB，and then selects two nodes with minimum number of potential connections to use the extension rules for complete RS.The experimental results show that this algorithm does not require any hardware or software modifications and can discover the＂dumb＂devices and guarantee discovering the topology which is compatible with the given input library.In the case of incomplete address forwarding table，it can discover physical layer topology in efficient，complete and accurate ways.

Heterogeneousmulti－subnet；Physical topology discovery；Dumb device；Address forward table

10.3969/j.issn.1002－2279.2015.01.010

TP393

A

1002－2279（2015）01－0029－06

内蒙古自然科学基金项目（2013MS0906）；内蒙古自治区高等学校科学研究项目（NJZY13102）；国家自然基金（61363052）

马晓波（1976－），女（蒙古族），内蒙古呼和浩特人，副教授，硕士，硕士生导师，主研方向：计算机网络，网络拓扑发现。

2014－09－11