基于Beam Search算法的集装箱装载问题研究

杨会志

摘 要：针对具有优先装载约束的集装箱装载问题，对Partial Beam Search算法进行了改进。在搜索过程中去除相似中间状态，增加了搜索过程的多样性，提高了算法的搜索效率。实验结果证明了算法的有效性。

关键词：集装箱装载问题；Beam Search算法；优先装载约束；搜索过程多样性

DOIDOI：10.11907/rjdk.151292

中图分类号：TP319 文献标识码：A 文章编号：1672-7800（2015）007-0106-03

0 引言

在集装箱的实际装载过程中，除了考虑最大化空间利用率之外，还要考虑多种约束因素，如：货物的摆放方向、某些货物的隔离性、货物的承载能力、货物装载的稳定性、装载的优先级、集装箱的承重性等。目前，针对货物装载过程中具有优先装载约束的研究成果还比较少，主要有Ren[1]等人提出的基于树搜索的方法，在该方法中，采用5个评价函数选择简单块。Ning Wang[2]等人提出的基于Partial Beam Search的方法，该方法改进了 Beam Search算法，定义了更加高效的块选择函数和完整装载方案的评价函数，计算效果优于Ren 等人提出的基于树搜索的方法。目前，满足C1和C2约束的集装箱装载问题的最好算法是I.Araya[3]等人提出的基于Beam Search的算法，该算法的最主要特点是运用Beam Search算法进行搜索时，通过去除搜索过程中产生的相似中间状态来提高搜索过程的多样性，进而提高搜索效率。

本文针对具有优先装载约束的集装箱装载问题，改进了Partial Beam Search算法，通过去除搜索过程中生成的相似中间状态来增加搜索过程的多样性，进而提高算法的搜索效率。

1 改进的具有优先装载约束的Partial Beam Search算法

根据Wenbin Zhu[4]等提出的集装箱装载算法分析框架，改进的具有优先装载约束的Partial Beam Search算法可以从以下6个方面进行描述。

1.1 空间表达方法

基于cover representation方法而不是cut representation方法进行装载空间表达，这是获得较高装载率的关键因素之一。

1.2 货物块种类

分别基于简单块和复合块，各用总体计算时间的一半来计算装载方案。在计算过程中不仅使用简单块，同时也使用复合块，这是获得较高装载率的关键因素之一。

1.3 选择装载空间

选择最佳装载空间遵循以下标准：①选择具有最小z轴坐标的可用空间；②如果满足上述标准的空间有多个，则选择具有最小Corner Distance的可用装载空间，见图1；③如果满足上述标准的空间有多个，则选择其中体积最大的空间；④如果满足上述标准的空间有多个，假设（x1，y1，z1）和 （x2，y2，z2）分别为可用装载空间的corner中离坐标原点最近和最远的点的坐标，按照（y1，z1，y2，z2，x1，x2）的次序依次选择具有最小值的空间。

图1 可装载空间与集装箱之间的Corner Distance

1.4 货物块选择策略

对状态S，在选择可用空间s后，可根据货物块的适应值最多选择m个货物块。设h（b）和l（b）分别为货物块b中优先装载的货物体积和非优先装载的货物体积。货物块的适应值函数f（s，b，S）为：

f（s，b，S）=h（b）+（l（b）-waste）·（1-l（S）/maxnh）（1）

其中waste是货物块b装载到空间s产生的浪费空间近似值，waste项前面的负号表示浪费空间越大的货物块，其适应值越小。l（S）是当前状态非优先装载货物的总体积，maxnh是装载方案中非优先装载货物和浪费空间的体积之和。货物块适应值函数的第一项倾向于装载优先货物，在适应值函数的第二项中，（1-l（S）/maxnh）是一个随非优先装载货物被装载到集装箱而不断减少的权重系数。

1.5 货物块放置方式

当货物块b放入到可用装载空间后，放在Anchor Corner，也就是具有最小Corner Distance的可装载空间的底角。

1.6 全局搜索算法

整体搜索过程采用基于Double Search Effort机制的Partial Beam Search算法。对一个给定的beamWidth值，当m设置为一个很小的值时，常常会得到一个很差的解，而如果m取值太大，计算过程耗时又太长。因此，采用多次运行Partial Beam Search优化过程进行计算。计算开始时以很小的搜索代价r=m2进行计算，然后加倍r的值再次进行计算，连续进行此类过程直到计算时间结束，而beamWidth作为算法的一个参数通过实验来确定它的最佳值。

Partial Beam Search算法如图2所示。每一次的搜索以stateList中包含一个代表空集装箱的状态开始。对每个stateList中的状态S，如果它不是一个装载方案的最终状态，算法将产生最多m=r个后继状态并加入到canList中。在所有下一层的候选状态都生成之后，开始评价每一个候选状态。在第一轮搜索，初始化搜索代价r=8，这个值对应搜索宽度m=2。在一轮搜索完成后，开始把r值加倍，得到m值后开始下一轮搜索。在给定的计算时间内连续进行多轮搜索，然后返回，找到最好的装载方案。

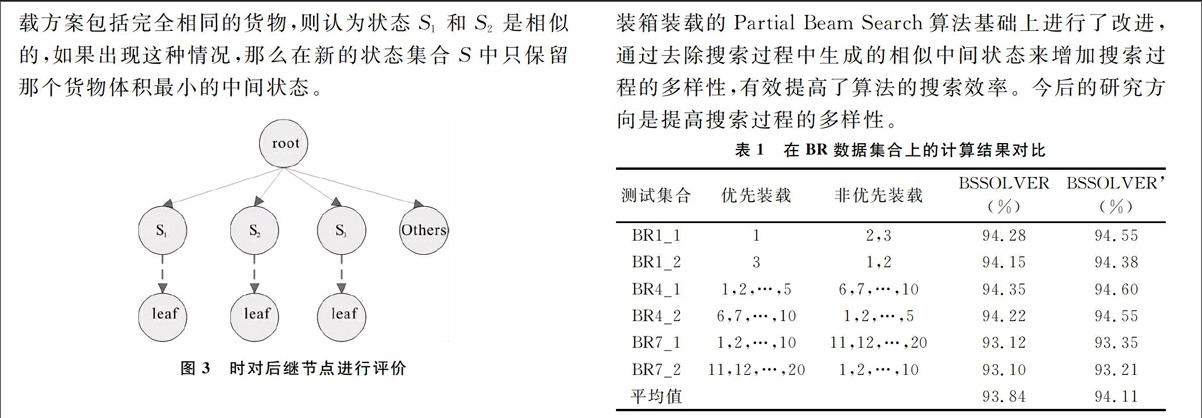
评价在状态S下生成的m个后继节点，采用一种深度受限制的树搜索算法，如图3所示。root节点对应要装载的一个货物块，对每个 root节点的后继节点状态的评价，采用连续装载适应值最好的货物块策略，直到完成所有装载过程。在得到所有的完整装载方案后，装载方案的评价函数由装载方案中优先装载货物的体积和装载方案总体积组成数据对，然后对所有装载方案所对应的数据对值进行降序排序，排序越靠前，函数值就越高。为了避免搜索过程收敛到相似的状态，提高搜索过程的多样性，在搜索过程生成新状态的集合S中去除相似的状态。规定如果搜索过程中的两个中间状态通过贪婪过程得到的装载方案包括完全相同的货物，则认为状态S1和S2是相似的，如果出现这种情况，那么在新的状态集合S中只保留那个货物体积最小的中间状态。

图3 时对后继节点进行评价

2 计算结果

表1是在BR数据集合上的改进算法与原有算法计算结果的对比情况，Partial Beam Search算法用BSSOLVER标识，本文算法用BSSOLVER标识。每个数据组包含100个实例，装载率的值是100个实例装载率的平均值。在Intel 酷睿2双核 T7200，2G内存计算机上，每个实例运行和BSSOLVER算法相同的时间400s。从表1可以看出，BSSOLVER算法在计算机性能较低的情况下，计算结果优于BSSOLVER算法，平均装载率提高了0.27%。

3 结语

本文针对具有优先装载约束的集装箱装载问题，在集装箱装载的Partial Beam Search算法基础上进行了改进，通过去除搜索过程中生成的相似中间状态来增加搜索过程的多样性，有效提高了算法的搜索效率。今后的研究方向是提高搜索过程的多样性。

参考文献：

[1] REN J ，TIAN Y ，SAWARAGI T. A tree search method for the container loading problem with shipment priority[J]. European Journal of Operational Research，2011：526-535.

[2] WANG N，LIM A，ZHU W. A multi-round partial beam search approach for the single container loading problem with shipment priority[J]. International Journal of Production Economics，2013，145（2）： 531-540.

[3] I ARAYA，M C RIFF. A beam search approach to the container loading problem[J]. Computers & Operations Research，2014（43）：100-107.

[4] ZHU W，OONW，LIM A，et al. The six elements to block-building approaches for the single container loading problem[J]. Applied Intelligence，2012，37（3）：1-15.

（责任编辑：杜能钢）