平顶高斯光束通过复杂光学系统的传输特性研究
杨利茹 王峰 王春芳
摘要: 为研究平顶高斯光束通过高斯光阑透镜系统的传输特性,基于光学矩阵的方法和Collins公式导出了平顶高斯光束通过该复杂光学系统后的场分布的解析表达式和近轴光强分布值,进而分析了平顶高斯光束通过高斯光阑透镜系统后的传输特性。研究结果表明,平顶高斯光束通过高斯光阑透镜系统后,实际焦点位置和几何焦点位置并不重合,即发生焦移现象。焦移量的大小与高斯光阑宽度及光阑与透镜间的距离等因素有关,即在一定条件下,光阑宽度增大,相对焦移量变小,光阑与透镜之间的距离与焦距的比越小,相对焦移量就越小。
关键词: 平顶高斯光束; 光阑透镜系统; 焦移
中图分类号: TN 012文献标志码: Adoi: 10.3969/j.issn.10055630.2015.03.015
Abstract: In this paper, we study propagation properties of flattened Gaussian beam passing through a Gaussian aperturelens system. Based on the optical matrix method and Collins formula, the analytical expression of field distribution and axial intensity distribution of flattened Gaussian beam passing through the complicated system are obtained. Propagation properties of the flattened Gaussian beam passing through Gaussian aperturelens system are analyzed. Results show that, as the beam passing through the optical system, the actual focus position is not at the position of the geometric focus, that is, the focal shift occurs. The focal shift is not only determined by the width of the Gaussian aperture, but also affected by the distance between the aperture and lens distance. Under certain conditions, if the aperture width increases, the relative focal shift diminishes. The ratio of the distance between the aperture and lens and focal length is smaller and the relative focal shift is smaller.
Keywords: flattened Gaussian beams; aperturelens system; focal shift
引言在激光的实际应用中,往往要求光束的光强为均匀的平顶分布,自从Gori提出一种新的平顶高斯光束以来[1],该模型便得到了广泛的研究[27]。由于实际光学系统经常受到光阑及透镜的限制,此类光学系统也很常见[810],但对于光阑透镜分离系统的研究却很少,尤其是精确的解析式更是难以获得。本文将采用光学矩阵的方法,将系统中的光学元件及传输路径都以矩阵形式表示出来,然后从Collins公式出发[11],得到精确的解析式,这对研究平顶高斯光束通过复杂光学系统提供了一种更为直观的方法。通过计算表明,平顶高斯光束通过高斯光阑透镜系统后,实际焦点和几何焦点位置发生偏移,即出现焦移现象,焦移量的大小与光阑宽度、光阑透镜间距离有关。
(2)式中以A、B、C、D表示的矩阵代表了一般系统,在该系统中可以分别表示成M4、M3、M2、M1 4个矩阵相乘的形式,Δz为出射面到透镜后焦面的距离。由Collins公式可推导出射面P处的横向光场分布E0(x0,z)=iλB∫∞-∞E0(x0,0)×exp-ik2B(Ax20-2xx0+Dx2)dx0(3)将式(1)、式(2)代入式(3),并用积分公式可得∫∞0x2nexp(-a2x2)cos(xy)dx=(-1)nπ122-2na-(2n+1)exp-y24a2H2ny2a(4)式中H2ny2a为2n阶的厄米特多项式。由此平顶高斯光束通过高斯光阑透镜系统的场分布公式转化为E(x,z)=ik2Bexp-ikD2Bx2N+1ω20+ikA2Bexp-kxB24N+1ω20+ikA2B×
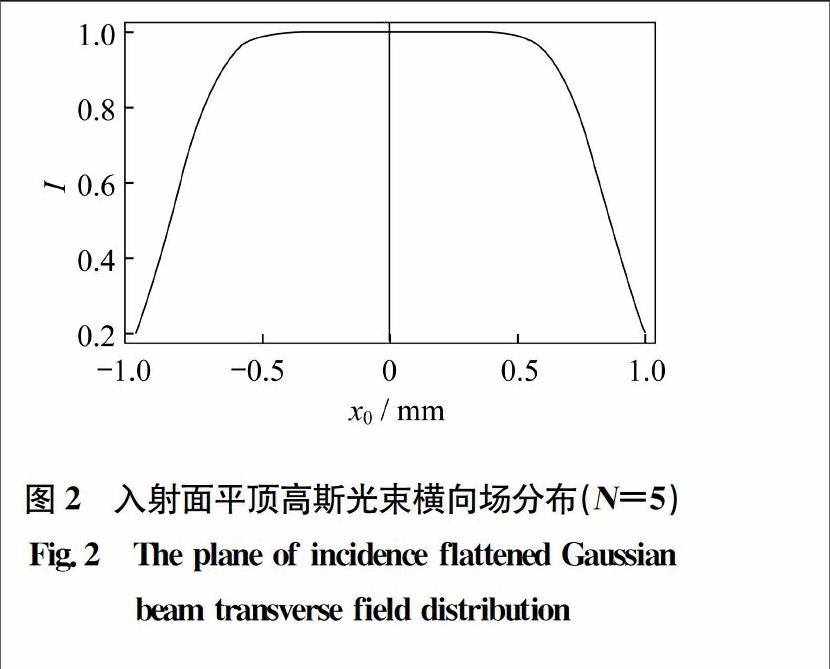
∑Nn=0-14n1n!N+1ω20nN+1ω20+ikA2B×H2nkxB2N+1ω20+ikA2B(5)为了便于绘图和分析,还需计算接收面的光强分布,其分布式为I(x,z)=E(x,z)×E*(x,z)(6)图2入射面平顶高斯光束横向场分布(N=5)
Fig.2The plane of incidence flattened Gaussian
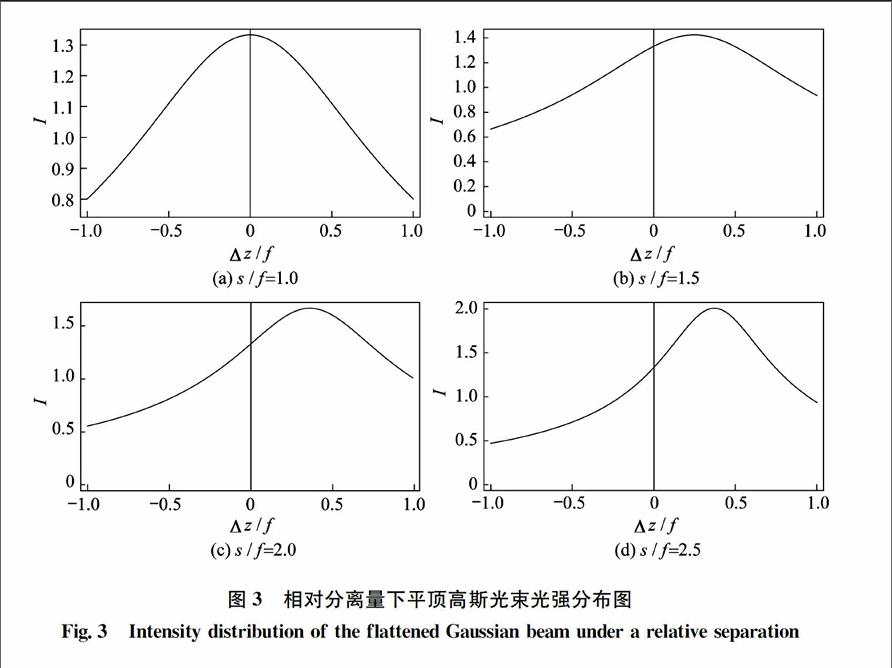
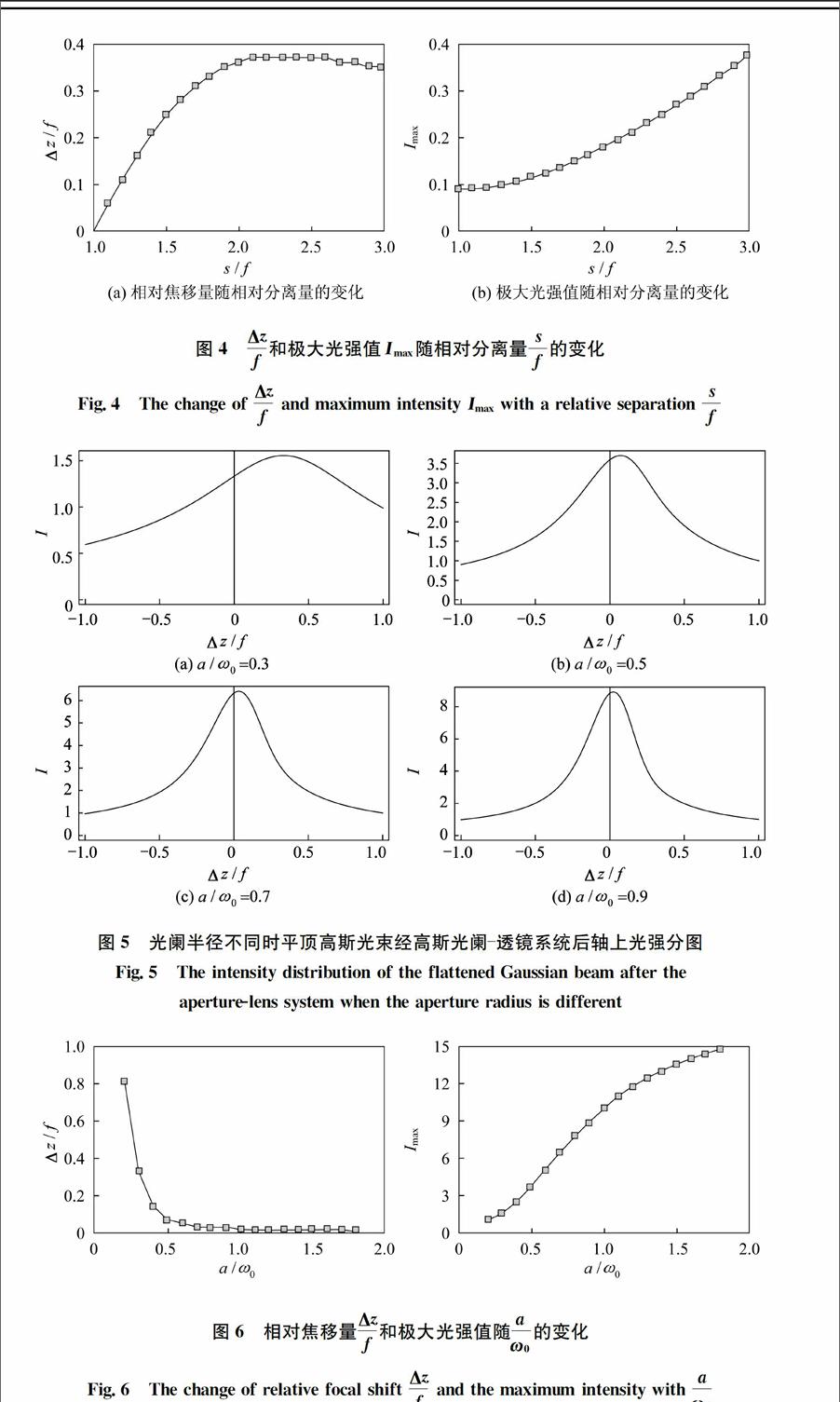
beam transverse field distribution2数值计算与分析设波长λ=1.06 μm,束腰宽度ω0为1 mm,薄透镜的焦距f为200 mm,平顶高斯光束的阶数N=5,高斯光阑的半宽a=0.3 mm。用Mathematica软件做出入射面平顶高斯光束的横向场分布图,如图2所示。取不同的s,以s与f的比值为变量,在其他参数与图2的参数一样的情况下做出平顶高斯光通过高斯光阑透镜系统后的轴上光强分布,见图3。在图3(a)~(d)中,高斯光阑与薄透镜的距离与焦距的比值分别为sf=1.0、sf=1.5、sf=2.0及sf=2.5。由图可以看出,高斯光阑与薄透镜之间的距离s与焦距的比(以下称相对分离量sf)越小,相对焦移量Δzf越小,光强极大值也越小。图4描述了相对焦移量Δzf、极大光强值Imax与sf的关系。考虑不同的高斯光阑的半宽a,其它参数与图2的参数一样,作出平顶高斯光束通过高斯光阑透镜系统后的近轴上光强分布图,见图5。图5(a)~(d),分别对应a/ω0=0.3、a/ω0=0.5、a/ω0=0.7和a/ω0=0.9,由图可以看出a/ω0越大,平顶高斯光束通过光学系统后产生的焦移量就越小,而极大光强值增加。这是因为当光阑增大时,衍射现象越来越不明显,当光阑增大到一定程度时,光线近乎直线传输,即光阑对光线的影响可近似忽略。此时,焦移量便越来越小,而极大光强(焦点处光强)就变得越来越大,如图6所示。
3结论以矩阵光学理论为基础,利用Collins公式研究了平顶高斯光束的传输规律。对平项高斯光束通过光阑透镜系统后其轴上光强分布和焦移进行详细研究,通过数值计算分析了各个参数对光强分布和焦移的影响,得到了精确直观的解析式。结果表明:光强分布和焦移不仅与高斯光阑宽度有关,还与光阑与透镜间的距离有关,即在一定条件下,光阑宽度增大时,相对焦移量变小,光阑与透镜之间的距离与焦距的比越小,相对焦移量越小。研究结果对准确确定高斯光束通过光学系统后实际焦点位置和焦点运动规律有指导意义,具有一定的实际应用价值。参考文献:
[1]GORI F.Flattened gaussian beams[J].Optics Communications,1994,107(5/6):335341.
[2]BORGHI R,SANTARSIERO M,VICALVI S.Focal shift of focused flattopped beams[J].Optics Communications,1998,154(5/6):243248.
[3]L B D,LUO S R.The pointing stability of flattened Gaussian beams[J].Journal of Modern Optics,2002,49(7):10891094.
[4]JI X L,L B D.Focal shift of flattened Gaussian beams passing through a spherically aberrated lens[J].OptikInternational Journal for Light and Electron Optics,2002,113(5):201204.
[5]罗时荣,吕百达.平顶高斯光束通过透镜序列的传输特性[J].激光技术,2003,52(12):143146.
[6]JIANG H L,ZHAO D M,ZHANG R M.Propagation characteristics of the rectangular flattened Gaussian beams through circular apertured and misaligned optical systems[J].Optics Communications,2006,260(1):17.
[7]肖希,赵光普,吕百达.平顶高斯光束通过硬边光阑传输算法的改进[J].激光技术,2005,29(1):106108.
[8]季小玲,吕百达.平顶高斯光束通过光阑透镜的焦移[J].激光技术,2003,27(1):5557.
[9]罗时荣,吕百达.平顶高斯光束在有光阑光学系统中的传输[J].中国激光,2002,29(5):425428.
[10]L B D,LUO S R.Approximate propagation equations of flattened Gaussian beams passing through a paraxial ABCD systems with hardedge aperture[J].Journal of Modern Optics,2001,48(15):21692178.
[11]COLLINS S A.Lenssystem diffraction integral written in terms of matrix optics[J].Journal of the Optical Society of America,1970,60(9):11681177.
(编辑:刘铁英)

