基于补偿分量的MMC最大调制系数的分析

刘一琦， 李宁宁， 傅裕， 王建啧， 纪延超

(哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨150001)

基于补偿分量的MMC最大调制系数的分析

刘一琦， 李宁宁， 傅裕， 王建啧， 纪延超

(哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨150001)

针对模块化多电平换流器(MMc)的相间环流问题，提出基于补偿分量的调制方法以便于降低MMc调制系数中的基频分量。首先通过结合实际系统中电容参数设计和换流器的正常运行范围，对MMc子模块电容电压纹波进行取值并求解其最大值，然后分析调制系数中抑制环流的补偿分量与电容电压纹波之间的数量关系，最终得到MMc最大调制系数的取值范围。仿真和实验验证的结果表明，通过对含有补偿分量的最大调制系数范围的确定，系统环流得到了有效抑制，避免了过调制现象的发生，有利于MMc系统的稳定运行。

补偿分量;环流抑制;模块化多电平换流器;调制系数;电容电压纹波

0 引 言

近年来随着风能和太阳能等可再生能源在分布式发电和大规模电站中的广泛应用［1］，电力电子变换器技术得到了快速发展，高压大功率能量转换系统的需求也日益增长［2-4］。模块化多电平变换器(modular multilevel converter，MMc)是一种新颖的多电平变换器拓扑结构，通过将多个相同子模块串联在一起，具有控制简单、存在公共的直流侧、突破了功率半导体器件容量的限制等优点，已成为高压大功率电能变换应用领域中的一种理想的解决方案［5-7］。但由于MMc在工作过程中，子模块电容的充放电导致了MMc的每相桥臂输出电压不同。因此，MMc存在子模块电容电压的均压、环流等明显的问题。其中，环流主要是由二倍频谐波分量构成［8-10］，采用开环的调制方法，从理论上消除了环流，但难点在于需要得到各电容电压的精确估计值［11］。闭环的调制方法［12］与开环的调制方法类似，都是引入一个附加分量到桥臂电压参考值中，补偿子模块电容电压的变化［13-14］。为了避免对MMc交流侧的影响，这个补偿分量被等量地加到上(下)桥臂中。

MMc的桥臂电压参考值由一个恒定的直流电压和一个基频分量组成。基频分量的幅值反映了换流器的调制系数，因此对桥臂电压参考值的限制决定了调制系数的大小。由于环流控制引入了补偿分量到桥臂电压参考值中，因此需要减小MMc调制系数的最大值从而避免过调制，但同时也降低了直流电压利用率，这在高压直流输电应用中是一个严重的问题。本文在考虑了环流抑制的前提下，详细地分析了MMc的数学模型，然后通过理论推导得到了含有补偿分量的子模块投入系数，基于上面的分析和投入系数的求解，得到了基于补偿分量法的最大调制系数的取值范围。最后通过比较仿真和实验结果验证了其正确性和合理性。

1 MMC的广义动态建模

三相MMc系统结构如图1所示。

MMc的子模块由2个带有反向续流二极管的全控型开关器件和1个直流储能电容构成［12］。通过采用平衡控制方法，假设每相桥臂上的不同子模块的电容电压相同。因此，MMc的每相桥臂电压可以表示为

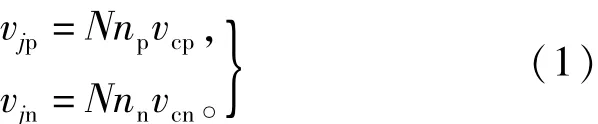
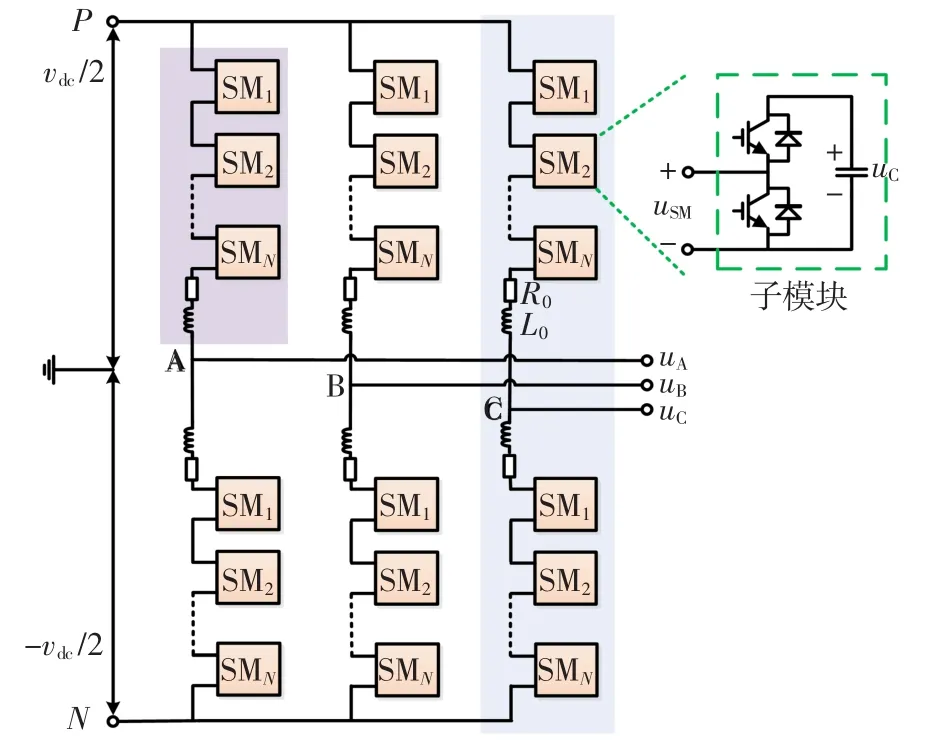
图1 三相MMC系统结构示意Fig.1 Three phase MMC main circuit structure

其中np和nn是投入系数。N是上(下)桥臂子模块的总数，vcp和vcn是上(下)桥臂子模块电容电压值，流过上(下)桥臂子模块的电流［15］可表示为

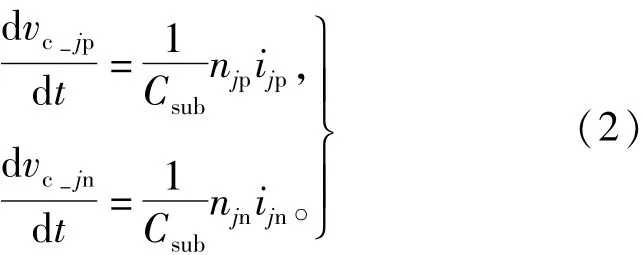
分别对第j相上(下)桥臂应用基尔霍夫电压定律可得

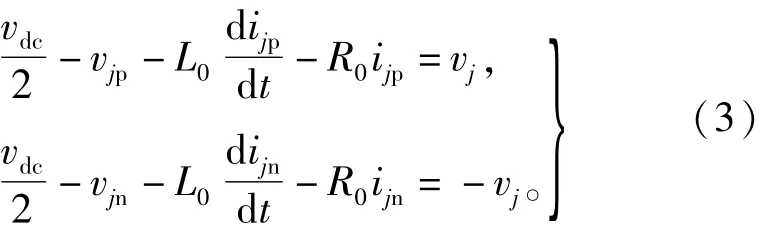
其中:L0和R0是桥臂电感与桥臂电阻，vdc是MMc的直流侧电压。由式(3)可知MMc交流侧和直流侧的电压模型为

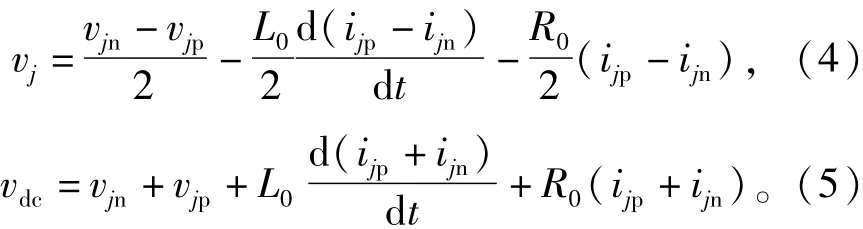
文献［16］中提出，由于环流控制会导致系统损耗增加，所以在投入系数中引入一个补偿分量，可以实现降低系统损耗。因此，含环流抑制的投入系数可定义为

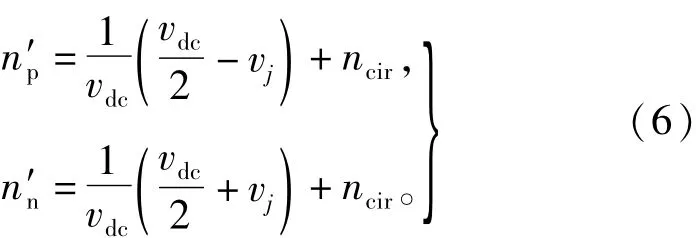
由式(6)可知，式(3)可以简化为

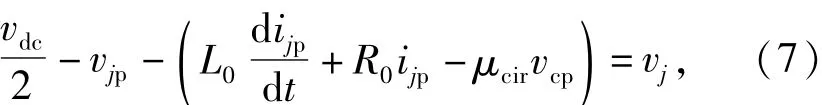
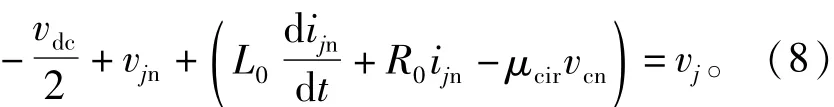
结合式(7)和式(8)，直流侧和交流侧等效模型如下:

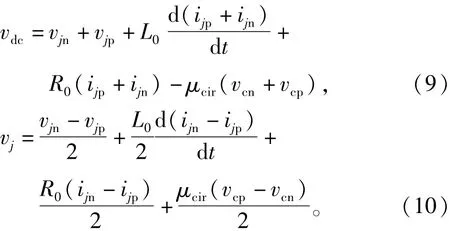
2 稳态值计算

在MMc中，通常将交流侧电流、直流侧电压和环流作为控制目标，结合上文中得到的数学模型，vcp+ccn，vcp-vcn的稳态值可以进行理论计算。然而，由于系统中同时存在基频分量和二次谐波分量使稳态值不能做到十分精确。首先可以忽略子模块电容电压纹波:

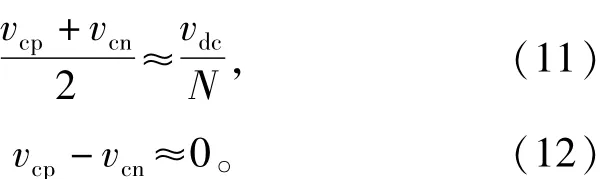
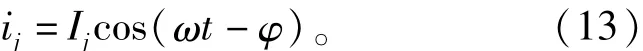
其中φ代表交流相电压和相电流的功角。

假设换流器无损耗，通过直流侧和交流侧的功率平衡:

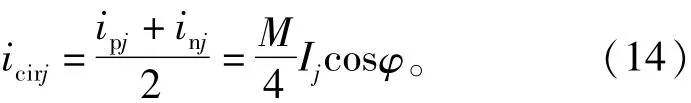
如果比较式(11)，式(12)中的近似值，可以发现最初的假设只有当Csub足够大时才能成立。从实际应用设计的角度考虑，Csub不可以太大否则换流器的成本会大大地增加。实际设计中将限制最大电容电压纹波在10%左右。电容电压纹波为［17］

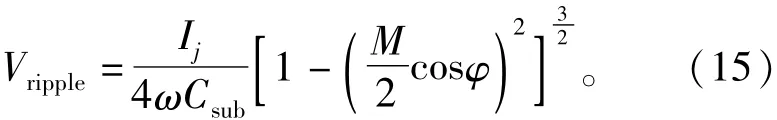
式(5)表明最大电容电压纹波取决于换流器运行范围，最大无功功率一般被定义为最大视在功率的一半，所以MMc运行在满载视在功率时最小功率因数为因此可以得到最大电容电压纹波

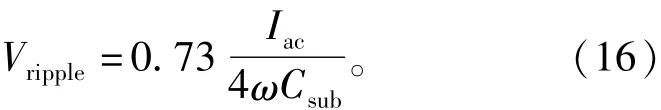
其中M的最大值为1，系数0.73与最大无功功率的约束相关。

如上述可知，环流控制将会加入一个补偿分量ncir到np和nn中。这个附加分量将会对上、下桥臂的投入系数产生影响，以至于影响MMc的调制系数的最大值。

3 补偿分量下调制系数最大值的计算

3.1 补偿分量的计算

被控的ijp+ijn只含有直流分量，考虑到R0相对很小，式(9)可简化为

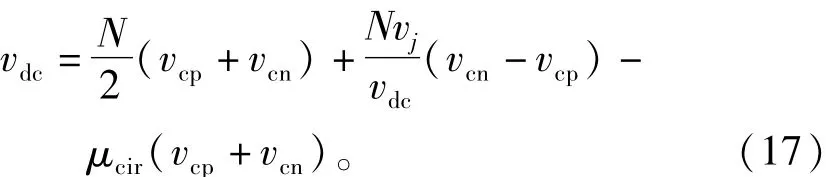
因此将式(11)带入上式得

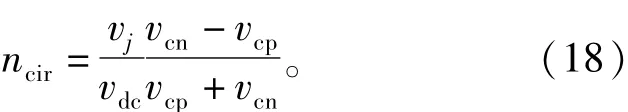
结合式(2)，式(6)，式(11)、式(12)和式(14)可得

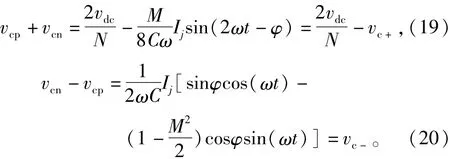
将式(19)和式(20)代入式(18)可以求得补偿分量的表达式为

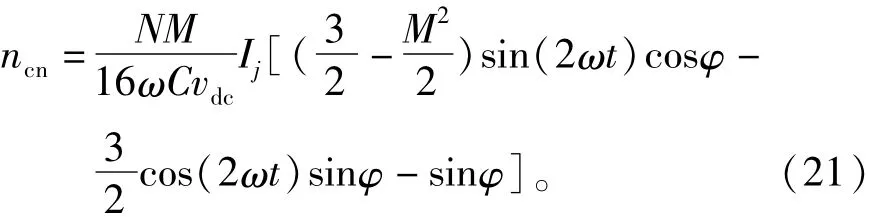
式(21)表明补偿分量是一个二倍频谐波，与系统参数(Csub、N)和运行条件(M、Iac和φ)有关。所以评估其对调制信号的影响并不方便。下面的数学运算可以用来简化ncir的表达。基于式(16)，子模块电容电压纹波的相对最大值可以被定义为

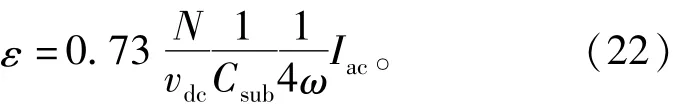
由于ε可以被看成一个固定值，则式(21)可以被简化为

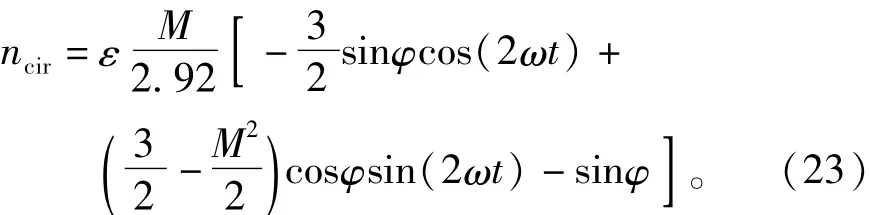
3.2 调制系数最大值的计算

上(下)桥臂的投入系数可以通过式(6)可得

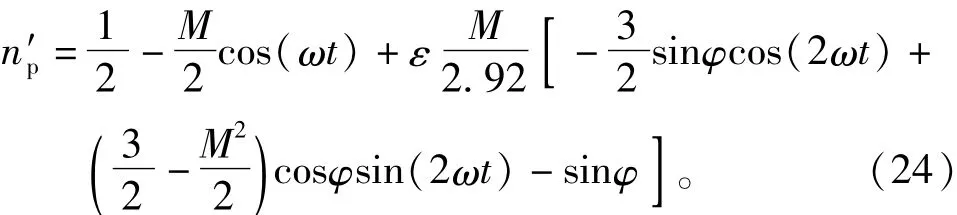
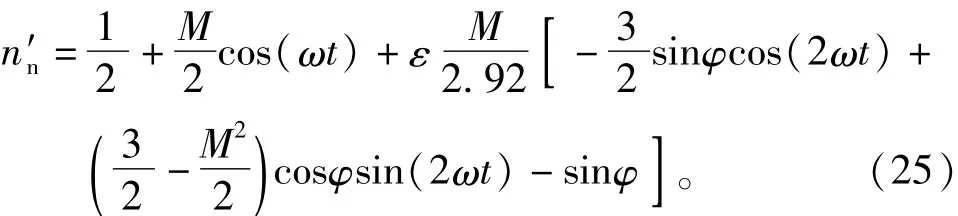
投入系数应该满足:

根据式(26)，上、下桥臂投入系数的最大和最小值可以在cosφ等于最小值的时候得到

所以可以得到调制系数的约束方程为

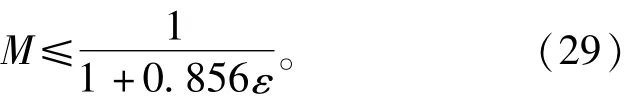
式(29)表明，调制系数最大值小于1，并且电容电压纹波越大会导致损耗越大。可以得出结论，如果假设子模块电容电压纹波为10%，则使用环流控制后调制系数的最大值将减少8%(从1到0.92);这些削减是不可以忽视的，而应该在MMc设计阶段就被考虑于额定调制系数的选取中。

4 仿真验证

为了验证上述理论计算和分析的正确性和可行性，在Matlab/SIMULINK仿真软件中搭建了MMc并网逆变器的模型。采用NLM调制策略，上(下)桥臂取反向的三角波与调制波进行比较，避免同向三角波与调制波进行比较过程中出现调制间隙导致开关器件频繁切换，减少切换损耗。系统参数见表1。

表1 MMC-HVDC系统参数Table 1 The parameters of MMC-HVDC system.

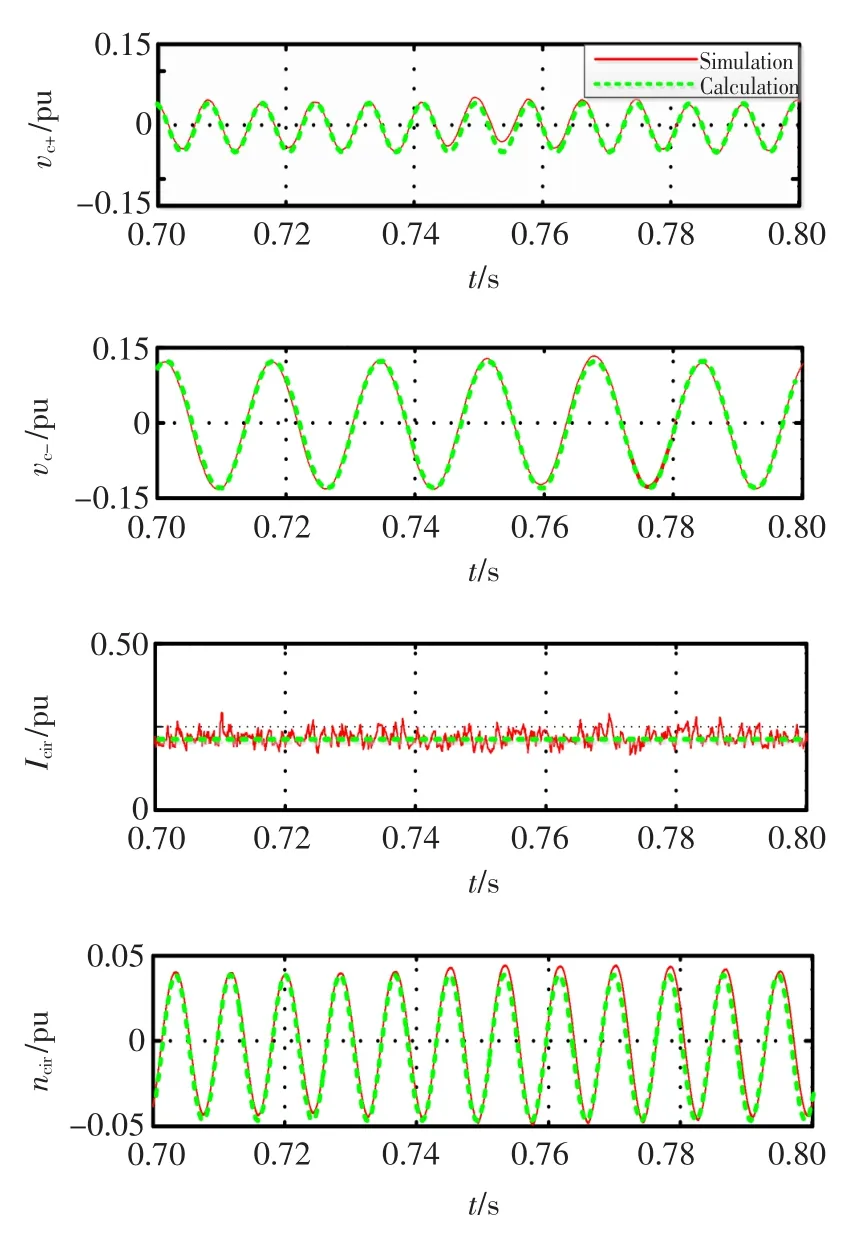
图2 稳态仿真结果Fig.2 Simulation results of steady state

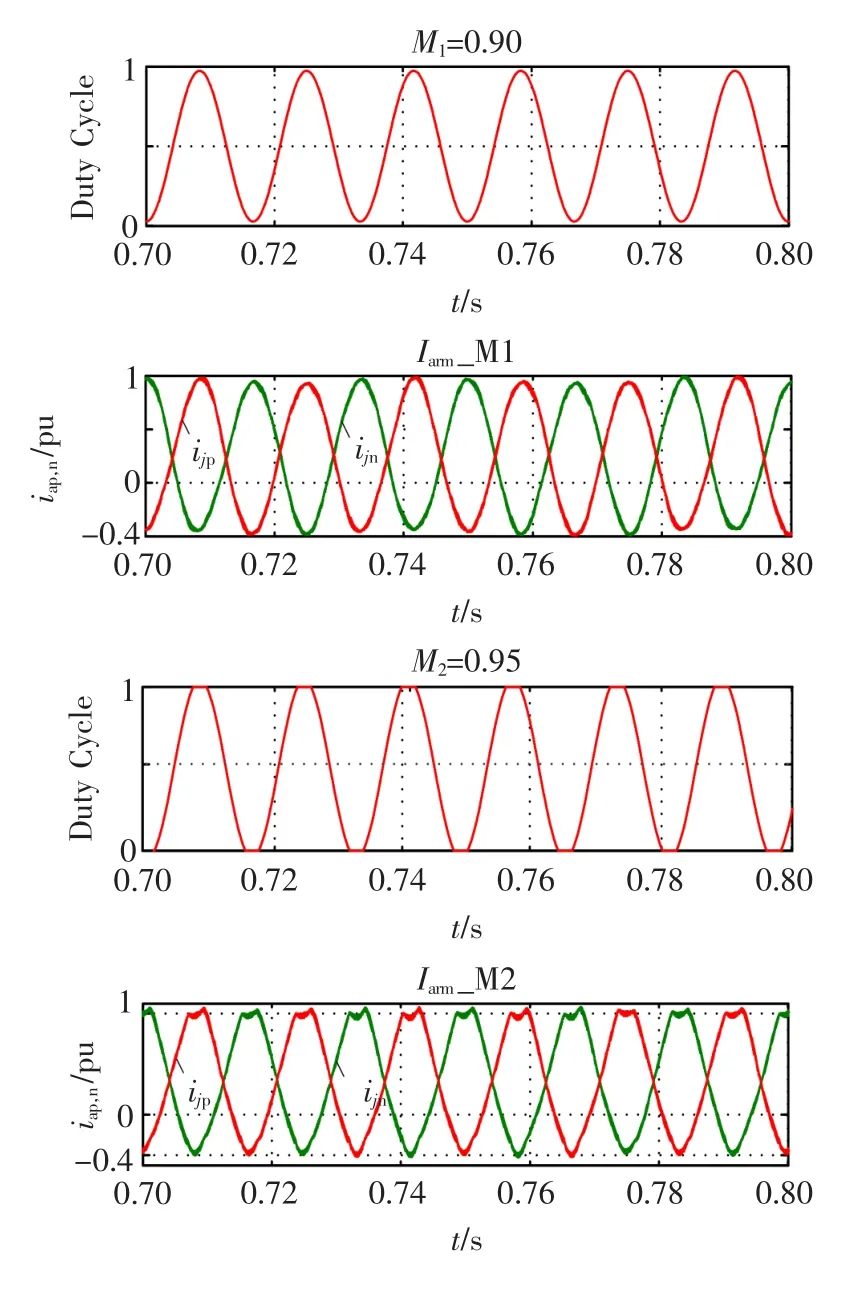
图3 在不同调制比条件下的电流信号Fig.3 The current signalwith differentmodulation indices

5 实验验证

为了验证MMc模型和调制系数最大值的正确性，研制了1 kW三相五电平的MMc实验样机，上(下)桥臂各有2个子模块，额定直流电压为100 V，子模块电容值为2 700μF，桥臂电感值为0.26mH。MMc直流侧连接一个恒定的直流电压源，运行在逆变状态，交流侧连接三相平衡的无源阻感负载。每相的电阻值为3.3Ω，电感值为5.5mH，为了模拟下限的运行情况，功角设定为30。。

在该样机中，由于死区的要求，每桥臂的调制指数最大值被限制到了0.98。在上述的系统参数下，相对电容电压波动设计越大，调制系数将越小。图4(a)说明了MMc达到稳态运行时，当调制系数按上述推导设定到约束条件的最大值0.92时，交流侧输出电压、电流和上(下)桥臂电流波形处于稳定运行状态，而MMc系统的相间的环流出现少数锯齿状波形，说明调制系数已经达到最大，如果超过0.92将会出现过调制现象。图4(b)是对投入系数中加入补偿分量后MMc子模块电容电压达到均衡运行的实验结果。因此可以证明，实验和仿真结果与理论分析基本一致，验证了理论分析的正确性和合理性。

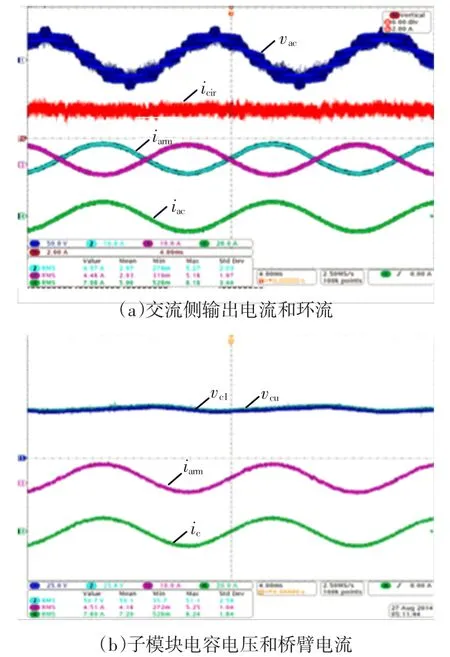
图4 稳态实验结果Fig.4 Experimental results of steady state

6 结 论

通过添加一个补偿分量为二倍频的补偿系数到含有环流控制的调制信号中，这个补偿分量会调节换流器最终的调制系数的大小，这将影响直流电压的利用率。因此得到调制系数最大值的削减量与子模块电容值有关，越小的电容值会导致越大的削减。如果电容被设计成满足10%的电压纹波要求，那么调制指数的最大值将减少8%。这个削减量不能被忽视，而应该在换流器设计时就考虑到额定调制系数的选取中。对于调制系数的合理考虑设计，会对系统的稳定运行和电容电压的均衡控制均会起到更佳的效果，保证了系统稳定运行的安全性和提高了系统功率传输的可靠性。

［1］ XIAONAN L，GUERRERO JM，KAIS，et al.Hierarchical control of parallel Ac-Dc converter interfaces for hybrid microgrids［J］.IEEE Transactions on SmartGrid，2014，5(2):683-692.

［2］ JM cARRAScO，L G FRANQUELO JT.BIALASIEWIcZ，et al. Power-electronic systems for the grid integration of renewable energy sources:A survey［J］.IEEE Transactions on Industrial Electronics，2006，53(4):1002-1016.

［3］ X LU，K SUN，JM.GUERRERO，et al.State-of-charge balance using adaptive droop control for distributed energy storage systems in Dc micro-grid applications［J］.IEEE Transactions on Industrial Electronics，2014，6(61)，2804-2815.

［4］ M GLINKA，RMARQUARDT.A new Ac/Dc multilevel converter family［J］.IEEE Transactions on Industrial Electronics，2005，52(3):662-669.

［5］ 刘钟淇，宋强，刘文华.基于模块化多电平变流器的轻型直流输电系统［J］.电力系统自动化，2010，34(2):53-58. LIU Zhongqi，SONG Qiang，LIU Wenhua.VSc-HVDc system based onmodularmultilevel converters［J］.Automation of Electric Power Systems，2010，34(2):53-58.

［6］ 管敏渊，徐政.模块化多电平换流器型直流输电的建模与控制［J］.电力系统自动化，2010，34(19):64-68. GUAN Minyuan，XU Zheng.Modeling and control ofmodularmultilevel converter in HVDc transmission［J］.Automation Power Systems，2010，34(19):64-68.

［7］ 管敏渊，徐政，屠卿瑞，等.模块化多电平换流器型直流输电的调制策略［J］.电力系统自动化，2010，34(2):48-52. GUAN Minyuan，XU Zheng，TU Qingrui，et al.Nearest levelmodulation for modular multilevel converters in HVDc transmission［J］.Automation of Electric Power Systems，2010，34(2):48 -52.

［8］ QINGRUI TU，ZHENG XU，LIE XU.Reduced switching-frequencymodulation and circulating current suppression formodular multilevel converters［J］.IEEE Transactions on Power Delivery，2013，26(3):2009-2017.

［9］ 屠卿瑞，徐政，郑翔，等.模块化多电平换流器型直流输电内部环流机理分析［J］.高电压技术，2010，36(2):547-552.

TU Qingrui，XU Zheng，ZHEN Xiang.et al.Mechanism analysis on the circulating current in modular multilevel converter based HVDc［J］.High Voltage Engineering，2010，36(2):547-552.

［10］ DORN J，HUANG H，RETZMANN D.A new multilevel voltage sourced converter topology for HVDc applications［c］//c I2 GRE Session.Paris，France:c IGRE，2008.

［11］ L ANGQUIST，A ANTONOPOULOS，D EMASZKO，et al. Open-loop control ofmodularmultilevel converters using estimation of stored energy［J］.IEEE Transactions on Industry Application.，2011，47(6):2516-2524.

［12］ A ANTONOPOULOS，L ANGQUIST，H P NEE.On dynamics and voltage control of the modular multilevel converter［c］//in Proc.European conf.Power Electronics and Applications (EPE)，Sept.2009:1-10.

［13］ YALONG L，EDWARD A JONES，FRED WANG.Switchingfrequency ripple in dc link voltage in a modular multilevel converter with circulating current suppressing control［c］//Proc. Applied Power Electronics conference and Exposition (APEc)，2014.

［14］ YALONG L，FREDWANG.Arm inductance selection principle for modular multilevel converters with circulating current suppressing control［c］//Proc.Applied Power Electronics conference and Exposition(APEc)，2013.

［15］ K.ILVES，A ANTONOPOULOS，S NORRGA，et al.Steadystate analysis of interaction between harmonic components of arm and line quantities ofmodular multilevel converters［c］//IEEE Transactions on Power Electronics，2012，27(1):57-68.

［16］ YALONG L，EDWARD A.JONES，FRED WANG.Analysis of the relationship between switching frequency and sub-Module capacitor unbalanced voltage for a modular multilevel converter［c］//Proc.Applied Power Electronics conference and Exposition(APEc)，2014.

［17］ S.ENGEL，RW DE DONc KER.control of themodularmultilevel converter forminimized cell capacitance［c］//in Proc.European Power Electronics and Application conference，2011.

(编辑:刘素菊)

Maximum modulation index analysis of MMC based on compensating component

LIU Yi-qi， LINing-ning， FU Yu， WANG Jian-ze， JIYan-chao
(School of Electrical Engineering and Automation，Harbin Institute of Technology，Harbin 150001，china)

Aiming at the circulating current in modular multilevel converter(MMc)，the modulation method was proposed based on compensating components to reduce the fundamental component in the modulation index.First，considering the parameter of capacitor design and the range of converter operation in practical system，capacitor voltage ripple in MMc was calculated，its maximum value was derived，and then the relationship between compensating component for eliminating circulating current in modulation index and capacitor voltage ripple was analyzed.Finally，the range of themaximum modulation index for MMc was obtained，and the simulation and experimentwere performed to verify the theoretical results.It is shown that by confirming the maximum modulation index with the compensated term，the circulating current can be effectively eliminated.At the same time，over-modulation is avoided，which ensures the stable operation of MMc.

compensating component;circulating current control;modularmultilevel converter(MMc); modulation index;capacitor voltage ripple

10.15938/j.emc.2015.04.009

TM 46

A

1007-449X(2015)04-0053-05

2014-09-06

科技部国际科技合作计划资助项目(2010DFR70600)

刘一琦(1984—)，男，博士研究生，研究方向为可再生能源功率变换和高压直流输电技术等;李宁宁(1982—)，男，博士研究生，研究方向为无功功率补偿，蓄电池储能等;傅 裕(1990—)，男，硕士研究生，研究方向为可再生能源功率变换和无功功率补偿技术等;王建赜(1972—)，男，研究员，研究方向为无功功率补偿、清洁能源并网控制等;纪延超(1962—)，男，教授，博士生导师，研究方向为无功功率补偿、有源滤波技术等。

刘一琦