基于改进单相dq变换与形态滤波的电压暂降检测方法

金显吉， 佟为明， 卢雷， 李凤阁

(哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨150001)

基于改进单相dq变换与形态滤波的电压暂降检测方法

金显吉， 佟为明， 卢雷， 李凤阁

(哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨150001)

针对电压暂降特征量检测时存在的实时性差、准确度低的问题，结合数学形态学理论和d-q变换原理提出了一种基于改进单相d-q变换与形态滤波的电压暂降检测方法。研究了改进单相d-q变换算法实现原理，构造了混合形态滤波器，并给出了滤波器结构参数选择依据。仿真分析了方法在理想电压暂降波形和含谐波电压暂降波形下的检测性能，并进行了实验验证。仿真分析和实验验证结果表明运用改进单相d-q变换可以快速准确地得到暂降幅值和相位;形态滤波能够去除检测结果中非直流量，计算量小、精确度高。

电能质量;电压暂降;形态滤波;dq变换;相位跳变

0 引 言

近年来，随着现代工业及高科技产业的飞速发展，以计算机、微处理器为核心的设备得到了广泛应用，它们对系统的扰动更敏感、对电能质量的要求更严苛。在各种电能质量问题中，电压暂降对于敏感设备影响最为严重，是导致其故障机损坏的主要原因，会造成巨大经济损失［1-3］。据统计，由电压暂降造成的经济损失占全部电能质量问题所造成的经济损失的70%～90%［4］。电压暂降不仅会造成经济损失，还可能造成人员意外伤亡和设备毁坏。例如医院的一些医疗保健设备、用计算机和微处理器控制的脑外科、心血管外科手术等，当发生电压暂降而造成设备不能正常工作时将带来严重后果［5］。因此对电压暂降进行监测是十分必要的，而准确地检测电压暂降的特征量，如暂降深度、持续时间与相位跳变是电压暂降监测的核心内容。

在电压暂降的检测方法中，较经典方法有:有效值法、缺损电压法、电压峰值法以及dq变换法等，也有学者将新的数学工具和信号处理方法如小波分析、傅里叶变换、神经网络，Dyn测度、分形测度等应用于电压暂降信号的检测［6-11］。这些算法都有其自身的局限性，适用与不同的场合。例如，有效值法无法给出电压暂降发生时可能出现的相位跳变，傅里叶变换法存在一个周波的延时，无法用于实时检测中。目前较常用的方法是基于dq变换原理的方法，对于dq变换法，其最大优点就是检测速度快，能够瞬时检测出暂降深度与相位跳变，且计算量小，但该算法受谐波畸变和噪声的影响较大，而且只能用于三相对称电压暂降的检测［12，13］。单相d-q变换法对传统d-q变换算法进行了改进，使其适用于单相检测，原理是根据单相电压构造α-β静止坐标系，再将α-β静止坐标系变换到d-q旋转坐标系，从而得到电压暂降的特征量。该方法能够适用于单相系统，但代价是增加了90。检测延迟，动态响应较差。另外，在实际配电网系统中，系统电压存在畸变和不平衡等问题，因此需要在d-q变换后的结果加低通滤波器，低通滤波器的时延特性给电压跌落的实时检测带来了困难，为了选择合适的低通滤波器，需要在滤波效果和时延两方面进行综合考虑。

本文提出的方法首先通过延时角度(理论上延时间角度可足够小)构造虚拟三相系统，然后进行dq变换，并用dq分解法计算出电压暂降深度和相位跳变，最后通过形态滤波器进行低通滤波，得到准确的基波电压暂降深度和相位跳变信息。方法中延时角度的减小，使得检测延时时间大幅减少，形态滤波器在电压暂降检测性能上也要优于传统的低通滤波器，具有检测计算量小、延时时间短、精度高等特点。改进单相d-q变换与数学形态滤波的结合提高了电压暂降检测是的实时性和精度。

1 改进单相d-q变换算法原理

利用理想三相电压波形相同、相位相差120。的特点，依据磁场等效原理，在单相系统中构造虚拟三相电压系统。

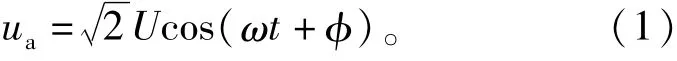
将ua延时60。，可以得到-uc，从而

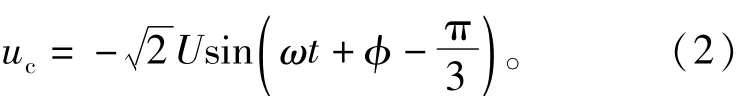
由于ua+ub+uc=0，因此

ua延时σ角度的电压uσ为

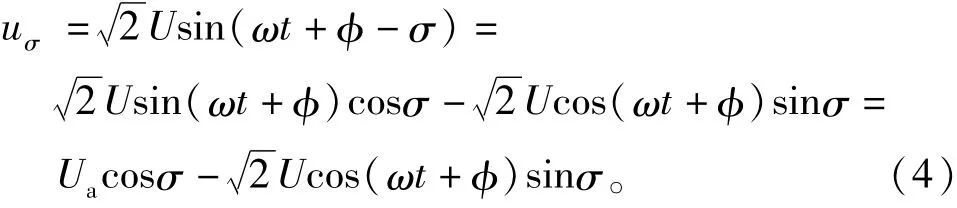
根据式(4)，可得

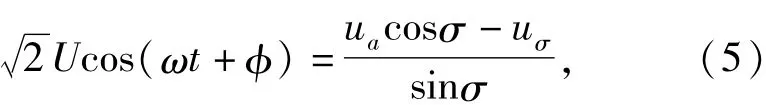
由式(2)和式(5)可得

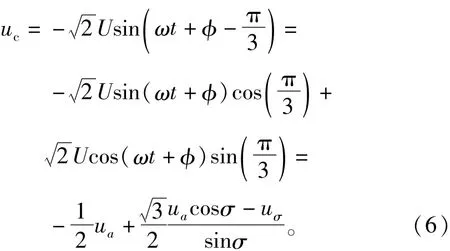
将式(6)代入式(3)可得

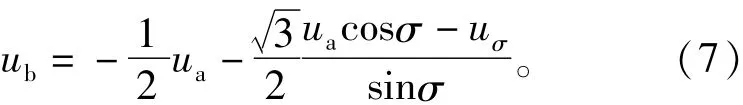
将三相电压变换到d-q轴

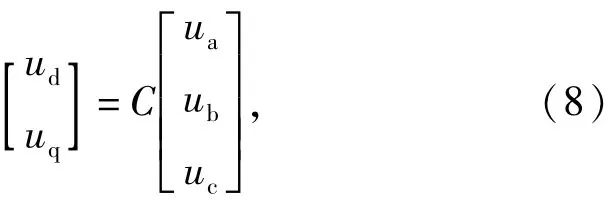
式中，

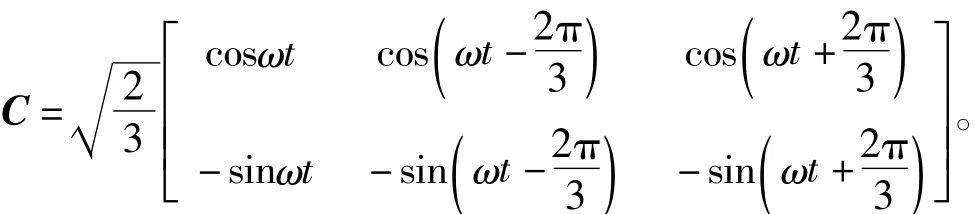
变换阵C中sinωt和cosωt是与a相电压同相位的正、余弦信号。将式(6)和式(7)代入式(8)，计算后可得

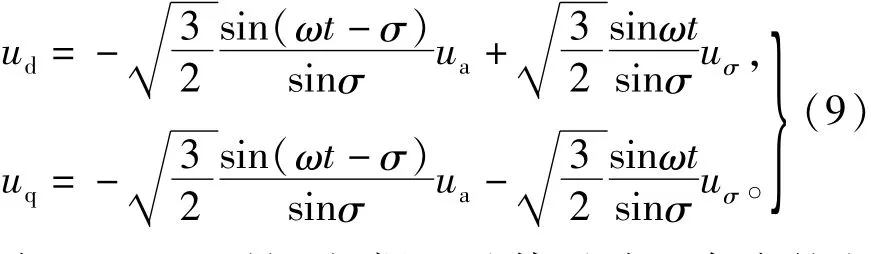
由于ua=u，所以根据u及其延时σ角度的电压值uσ计算ud、uq有

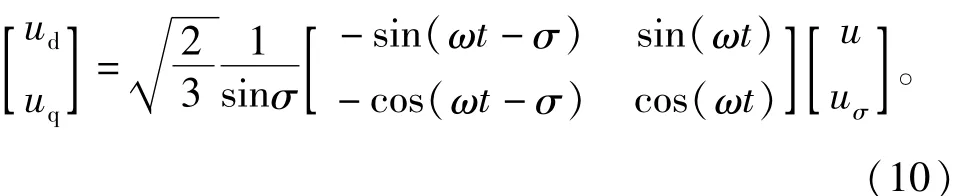
根据ud、uq即可求出单相电压u的有效值与初始相位

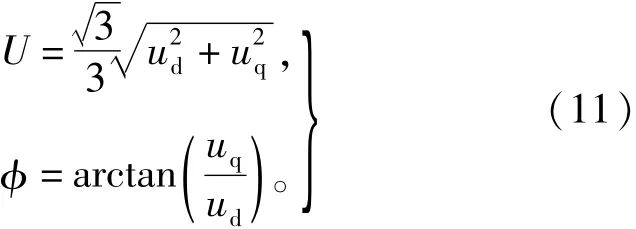
理论上，此改进算法所需的延时角度σ可以任意小，从而虚构信号与实际信号的延时可任意小，采用式(11)的检测延时可接近于0。但是，当σ太小时很大，使得u、u的计算结果受u的噪声影dq响较大，因此σ的取值不宜太小。

2 形态滤波

2.1 形态滤波器的构造

数学形态滤波是建立在数学形态学基础上，利用结构元素在信号中不断移动，考察信号各部分之间的相互关系，提取有用特征的方法。形态变换一般分为二值形态变换和灰度(多值)形态变换，其基本运算包括膨胀、腐蚀以及由此引出的开、闭运算等［14-15］。形态运算主要是布尔运算和少量的加减运算，与一般低通滤波器相比，计算简单且延时短。由于本文的研究对象为电网中的电压采样信号，属于一维多值信号，也可看作是一维灰度图像，因此下面给出一维灰度形态变换的4种基本运算定义。

设f(x)和b(x)分别为输入信号和结构元素，长度分别为N和M，且N≥M，则f(x)关于b(x)的腐蚀运算和膨胀运算分别定义为

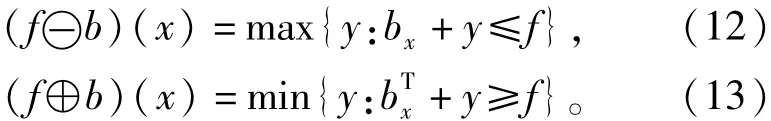
式中，bx表示将沿横轴平移x的结构元素表示关于原点对称的结构元素。

从几何角度讲，为求出点x处的腐蚀结果，应将结构元素从原点平移到x点，然后再向上推，始终保持结构元素位于输入信号的下方，能够向上推动的最大值即为该点的腐蚀结果。膨胀运算依然与腐蚀运算互为对偶，x处的膨胀结果是通过将b的对称结构元素bT平移到x处再上推，使得在bTx的定义域内bTx完全位于信号上方(在输入信号的无定义处，将其值视为负无穷)，此时bTx的上推高度的最小值即为该点的膨胀值。除式(12)和式(13)外，腐蚀和膨胀还有一种在程序上较为容易实现的表达式为

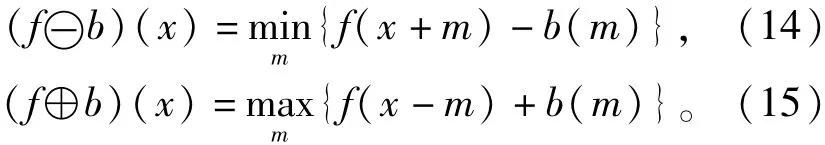
式中结构元素b以m为自变量。

膨胀和腐蚀运算是不可逆运算，先腐蚀后膨胀被定义为开运算;先膨胀后腐蚀被定义为闭运算。利用式(14)和式(15)定义的形态膨胀、腐蚀运算，则一维灰度形态开运算和闭运算可分别定义为

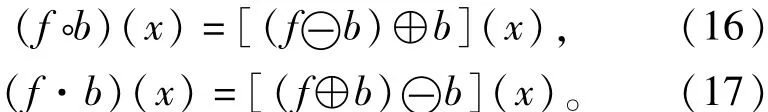
对于含有毛刺噪声的一维输入信号，可通过灰度开/闭运算进行滤波。开运算可以从信号波形的下方对波形进行平滑，消除正尖峰噪声;闭运算则从信号波形的上方对波形进行平滑，消除负尖峰噪声。而在实际采样信号中通常同时包含这两种噪声。为了能够同时滤除正、负脉冲噪声，可对开运算和闭运算进行级联。由此便形成了开-闭(Oc)和闭-开(co)两种形态滤波器，其定义分别为

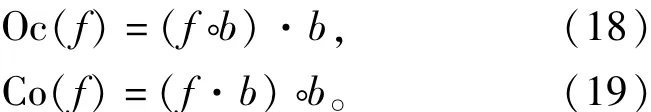
两种滤波器均有较好的低通滤波效果，但是当噪声密度较高时，两种滤波器的输出均会产生向上或向下的偏移。

根据改进单相dq变换后的电压信号组成特征，如果选择合适的结构元素和相应的宽度，则对变换后的信号进行co和Oc运算后，直流分量可以保留，而信号中混杂的宽度小于结构元素宽度的谐波分量将被消除，从而得到暂降深度和相位跳变。同时考虑到co和Oc滤波器均存在统计偏移现象，单独使用上述两种滤波器均不能取得理想的滤波效果，因此，为了消除这种偏移，本文采用两种滤波器平均组合形式，构造混合滤波器为

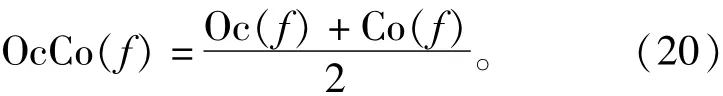
2.2 滤波器结构元素参数选择

在结构元素的选择上，要使其尽可能小，同时结构要尽可能接近待分析信号的图形特点。根据待处理电压信号的特点，由于要保留的是直流分量，故需采用扁平型结构元素。

实际电网中的电压信号含有大量的谐波，根据形态滤波器的特点，为仅保留电压信号中的直流分量，需使结构元素的宽度大于最低次谐波半个周期的宽度。虽然结构元素宽度越长，则滤波器的低通能力越强，滤波效果越好，但是动态响应时间也随着增大。因此，综合考虑滤波效果和动态响应时间，结构元素宽度应略大于最低次谐波半个周期的宽度。例如，在采样频率为12.8 kHz(每周波采样256点)的情况下，为了能滤除2次以上的谐波，结构元素的长度取为65较为合适。另外，为减少形态运算的计算量并减少偏移量，结构元素的值选择为0。

3 方法的实现

综上所述，采用改进单相dq变换结合数学形态滤波器对电压暂降进行检测的算法实现原理如图1所示。

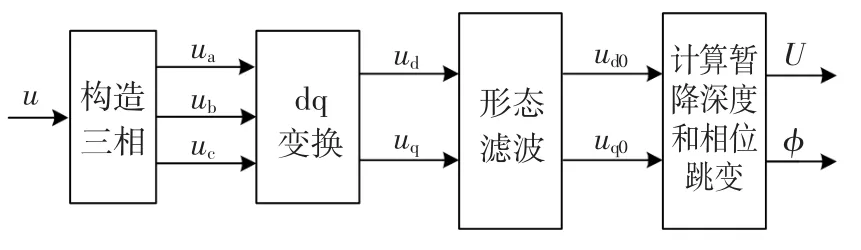
图1 检测算法原理Fig.1 Princip le diagram of detection algorithm

用本文提出的新方法对电压暂降进行检测的主要步骤如下:

步骤1)将单相系统构造成虚拟的三相系统;

步骤2)根据式(8)将三相电压变换到d-q旋转坐标系下，并结合式(9)和(10)得到d轴分量(ud)和q轴分量(uq);

步骤3)利用构造的形态滤波器进行低通滤波得到dq电压分量中的直流成分ud0和uq0;

步骤4)根据式(11)计算暂降电压信号的暂降深度和相位跳变。

4 方法性能仿真分析

4.1 理想电压暂降波形下检测方法比较

利用Matlab对某一单相电压暂降采用改进单相d-q变换方法进行检测，并与目前广泛应用的有效值法和传统单相d-q变换方法进行比较。

设定电压暂降信号表达式为

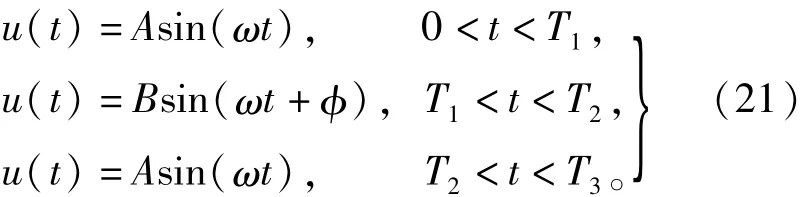
式中，A为暂降发生前和恢复后的电压瞬时值，B为发生暂降的电压瞬时值，T1和T2为暂降开始和结束的时间，T3为仿真信号的结束时间，φ为相位跳变。

仿真中设定该相电压有效值为100 V，频率为50 Hz，电压暂降发生在60～160ms之间，暂降深度为50%，暂降起始时刻发生了-60。相位跳变。理想电压暂降波形如图2所示，该波形采样频率为12.8 kHz(每周波采样256点)。检测时改进方法的延时角度取σ=11.25。。

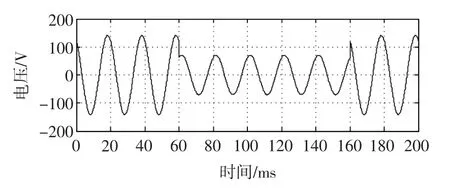
图2 理想电压暂降波形Fig.2 Ideal voltage sag waveform

图3为3种方法电压暂降深度检测结果的比较。其中，图3(a)为有效值法，图3(b)为传统单相d-q变换法，图3(c)为改进单相d-q变换法。

图3 电压暂降深度直接检测结果Fig.3 The direct detection result of sag dep th

由于相位跳变的检测结果与暂降深度的检测结果趋势相同，故文中仅从电压暂降深度角度对3种方法进行了比较。

由图3可以看出，有效值法在检测电压暂降时，能够较为准确地检测出暂降深度值，并且抗噪声干扰能力较强。但该方法在准确检测出暂降深度前，会经历一个周期的过渡期，这是由暂降发生前的“历史数据”所引起的。过渡期内检测到的有效值既不是暂降前的正常电压有效值也不是暂降后的有效值，而是介于二者之间的值。此外过渡期还导致了暂降持续时间的减小，图中可以明显看出该方法得到的暂降持续时间比实际少了近一个周期。因此，有效值法虽然在计算暂降深度时较为准确，但不能准确地给出暂降的起止时刻，也无法给出相角跳变。

传统单相dq变换法可通过两个间隔90。的采样点计算得到当前的电压有效值与相位，对暂降深度及相角跳变的检测比较精确，计算量很小。但延时大(90。的检测延时)，实时响应特性不够好。

改进后的单相dq变换方法，继承了传统单相dq变换法的准确度高、计算量小等优点，并在动态响应时间上有了明显的改善(在本文的算例中检测延时仅为11.25。)，提高了检测实时性。但其看抗干扰性能仍较弱，需要后续合理的滤波处理。

3种电压暂降检测方法的特点如表1所示。

表1 3种电压暂降检测方法特点Table 1 Detection features for three kinds of voltage sags

4.2 含谐波电压暂降检测结果滤波效果比较

通常情况下电网中的电压信号中会有一定的谐波成分，利用改进单相d-q变换进行电压暂降检测时，被测电压u的基波分量表现为ud、uq中的直流量，而u的h次谐波分量表现为ud、uq中的h+1次谐波和h-1次谐波。因此当电压信号主要含3、5、7次谐波时，经过变换后会变现为2、4、6、8次谐波。这就需要通过低通滤波器滤波以得到ud、uq的直流量ud0和uq0。滤波器会影响到检测的精度和延时时间。为了验证本文构造的形态滤波器滤波性能，下面对常用的二阶巴特沃斯低通滤波器和本文构造的数学形态滤波器的滤波性能进行比较。

仿真模型中电压信号的基本参数与无谐波时相同，只是注入谐波成分(5次谐波含量2%，7次谐波含量5%)，含谐波的电压暂降波形如图4所示。

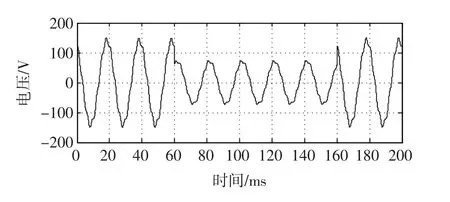
图4 含谐波的电压暂降波形Fig.4 Voltage sag waveform w ith harmonic

采用改进单相dq变换结合二阶巴特沃斯滤波器与采用改进单相dq变换结合形态滤波器，对电压暂降检测结果进行滤波时，检测到的电压暂降深度结果如图5所示，检测到的电压暂降相位跳变结果如图6所示。

通过图5和图6中使用巴特沃斯滤波器和使用形态滤波器对电压暂降结果进行滤波后的结果可以看出:采用传统巴特沃斯滤波器延时较长，精度也稍差;而形态滤波器延时短，精度也较高，且可以精确确定暂降发生起止时刻，在检测性能上明显优于巴特沃斯滤波器。除此以外，形态滤波器的计算量要小于巴特沃斯滤波器。因此在电压暂降检测性能上形态滤波器要优于巴特沃斯滤波器。

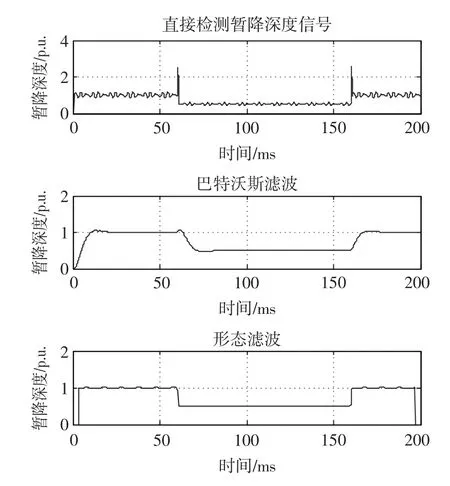
图5 使用形态滤波器和巴特沃斯滤波器的电压暂降深度检测结果滤波效果比较Fig.5 Comparison of filtering effects for detection results of sag depth between m orphological and butterworth filter

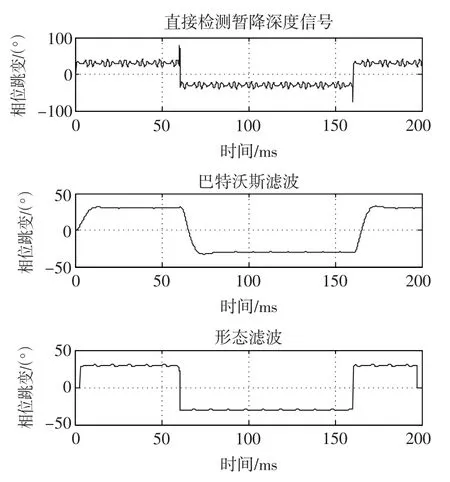
图6 使用形态滤波器和巴特沃斯滤波器的电压暂降相位跳变检测结果滤波效果比较Fig.6 Comparison of filtering effects for detection results of phase angle jum p between morphological and butterworth filter

5 实验验证

为验证方法的有效性，在自行开发的电能质量监测装置中对所提方法的检测性能进行了实验验证。利用GDS-1102信号发生器的衰减功能产生一个深度为0.1p.u.、相角跳变为0。的电压暂降信号，在c c S软件中对装置的暂降检测效果进行观察(采样率为每周波256点，延时角度为11.25。)。

图7为装置通过故障录波功能记录的电压暂降波形，图8(a)、图8(b)和图8(c)分别为与之对应的暂降扰动点、暂降深度、相位跳变检测结果。

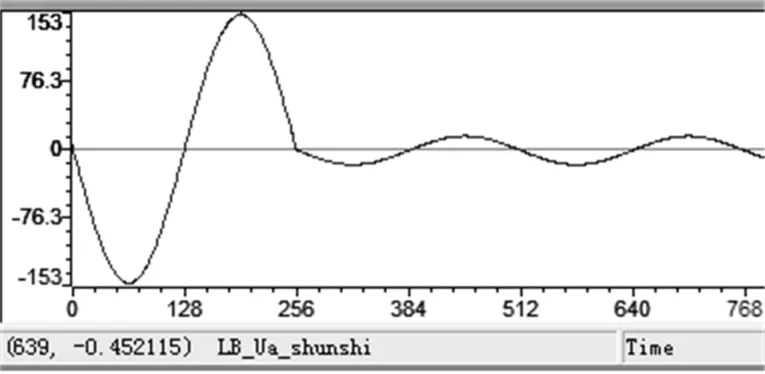
图7 故障录波记录的暂降波形Fig.7 Voltage sag waveform of fault record

从实验结果可以得出，暂降扰动检测延时仅为为0.6ms左右，较传统单相d-q变换法5ms左右的延时有较大提升，暂降深度的检测误差小于0.001p.u.，相位跳变的检测误差小于0.1。，可见新方法对电压暂降特征量的检测具有较高的快速性和准确性。

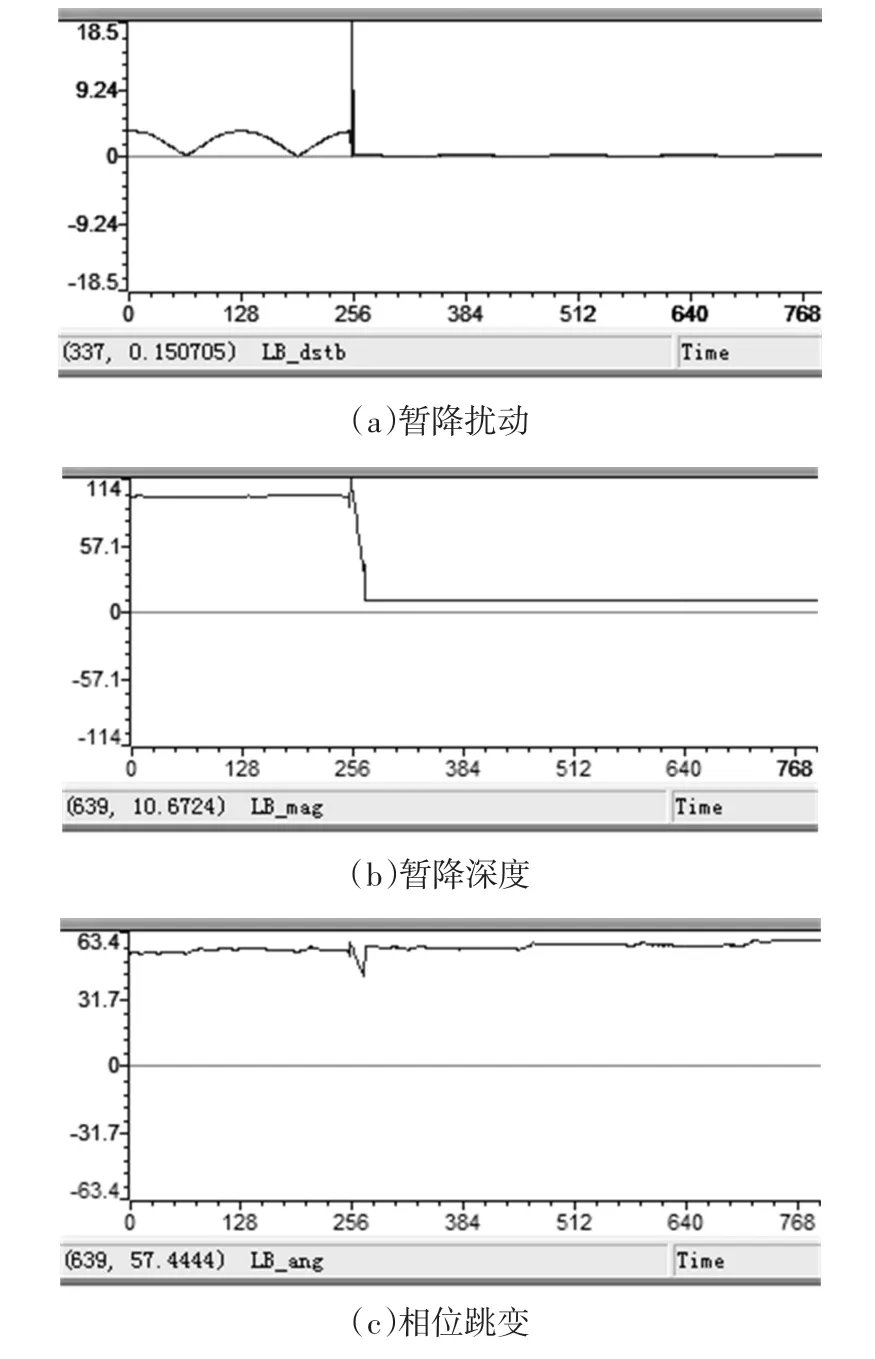
图8 电压暂降检测实验结果Fig.8 The experimental results of voltage sag detection

6 结 论

本文提出了一种电压暂降检测的新方法。改进单相dq变换方法所需的延时角度理论上可以为任意小，较传统方法能更快速估计电压暂降发生过程中基波电压有效值和初相位，检测精度也较高;形态滤波具有数据处理窗短、运算速度快等优点，所构造的形态滤波器在电压暂降检测滤波性能上要优于传统的低通滤波器。二者的综合运用，提高了电压暂降检测的实时性和准确性，这对动态电压补偿与恢复是有实质意义的。

［1］ 吕干云，孙维蒙，汪晓东，等.利用三点法的电压暂降源定位方法［J］.中国电机工程学报，2011，31(7):25-26. LÜGanyun，SUNWeimeng，WANG Xaiodong，etal.Voltage Sag Source Location Based on Three-point Method［J］.Proceedings of the c SEE，2011，31(7):25-26.

［2］ NIELSEN JG，NEWMAN M.control and testing of a dynamic voltage restorer(DVR)atmedium voltage level［J］.IEEE Trans on Power Electronics，2004，19(3):806-813.

［3］ 曹立志，王小君，和敬涵，等.基于DSP的电压暂降检测方法研究［J］.电力系统保护与控制，2012，13:78-83.c AO Li-zhi，WANG Xiaojun，HE Jinghan.Research of voltage sag detection methods based on DSP［J］.Power System Protection and control，2012，13:78-83.

［4］ GOMEZ J c，MORcOSM M.Voltage Sag and Recovery Time in Repetitive Events［J］.IEEE Transactions on Power Delivery，2002，17(4):1037-1043.

［5］ LEE D M，HABETLER TG，HARLEY RG，etal.A voltage sag supporter utilizing a PWM-switched autotransformer［J］.IEEE Trans on Power Electronics，2007，22(2):626-635.

［6］ 刘连光，贾文双，肖湘宁，等.用小波变换和有效值算法实现电压凹陷的准确测量［J］.电力系统自动化，2003，27(11):30-33. LIU Lianguang，JIA Wenshuang，XIAO Xiangning，et al.Measurementmethod of voltage sag bywavelet transform and RMSmethod［J］.Automations of Electrical Power Systems，2003，27(11): 30-33.

［7］ 赵凤展，杨仁刚.基于短时傅里叶变换的电压暂降扰动检测［J］.中国电机工程学报，2007，27(10):28-34. ZHAO Fengzhan，YANG Rengang.Voltage sag disturbance detection based on short time Fourier transform［J］.Proceedings of the c SEE，2007，27(10):28-34.

［8］ 李承，杨博，邹云屏，等.基于反馈神经网络的电压暂降特征量实时检测方法［J］.电机与控制学报，2010，14(9):19-25. LI cheng，YANG Bo，ZOU Yunping，et al.Voltage sag real-time detectionmethod based on feedback neural network［J］.Electric Machines And control，2010，14(9):19-25.

［9］ 刘应梅，白晓民，王文平，等.基于Dyn测度的电压暂降检测方法［J］.电力系统自动化，2004，28(2):45-49. LIU Ying-mei，BAIXiao-min，WANGWen-ping，et al.A Dynamics-based method for voltage sags detection［J］.Automations of Electrical Power Systems，2004，28(2):45-49.

［10］ 李智勇，吴为麟.基于分形测度的电压暂降持续时间检测［J］.电工技术学报，2007，22(9):148-153. LIZhiyong，WU Weilin.Voltage sag duration detecting method based on fractal numbermeasurement［J］.Transactions of china Electrotechnical Society，2007，22(9):148-153.

［11］ ENRIQUE Perez，JULIO Barros.An extended Kalman filtering approach for detection and analysis of voltage dips in power system［J］.Electric Power Systems Research，2008，78(4):618 -625.

［12］ 常学飞，田立军，秦英林.一种精确确定电压暂降凹陷域的算法［J］.电力自动化设备，2011，31(4):64-68. c HANG Xuefei，TIAN Lijun，QIN Yinglin.Method to accurately determine vulnerable areas of voltage sag［J］.Electric Power Automation Equipment，2011，31(4):64-68.

［13］ FITZER c，BARNESM，GREEN P.Voltage sag detection technique for a dynamic voltage restorer［J］.IEEE Trans on Industry Applications，2004，40(1):203-212.

［14］ 陈平，李庆民.基于数学形态学的数字滤波器设计与分析［J］.中国电机工程学报，2005，25(11):60-65. c HEN Ping，LIQingmin.Design and analysis of mathematical morphology-based digital filters［J］.Proceedings of the c SEE，2005，25(11):60-65.

［15］ 欧阳森，王建华，宋政湘，等.基于数学形态学的电力系统采样数据处理方法［J］.电网技术，2003，27(9):61-65. OUYANG Sen，WANG Jianhua，SONG Zhengxiang，et al.A new power system sampled data processingmethod based onmorphology theory［J］.Power System Technology，2003，27(9):61 -65.

(编辑:于智龙)

A detection algorithm of voltage sag based on improved single-phase dq trans for mation and morphological filtering

JIN Xian-ji， TONGWei-ming， LU Lei， LIFeng-ge
(School of Electrical Engineering and Automation，Harbin Institute of Technology，Harbin 150001，china)

Aiming at the problems of bad real time capability and low accuracy on voltage sag characteristic quantity detecting and combined with mathematicalmorphology and dq transformation，a new algorithm for voltage sag detection was presented，which integrates improved single-phase dq transformation with morphological filtering.The principle of improved single-phase dq transformation algorithm was studied，and amixedmorphological filterwas constructed with structure parameters given.The detection performances of the proposedmethod using in ideal voltage sagwaveform and containing harmonic voltage sag waveform were analyzed by simulating，and the results have been verified through experiments.The results of simulation analysis and experimental verification show that the amplitude and phase angle of voltage sag can be got quickly and accurately by using improved single-phase dq transformation and morphological filtering is used to remove Ac componentswhich is low computational complexity and high precision.

smart grid;voltage sag;morphological filtering;dq transformation;phase angle jump

10.15938/j.emc.2015.04.008

TM 761

A

1007-449X(2015)04-0046-07

2014-01-16

国家自然科学基金(51077015，50907014);中央高校基本科研业务费专项资助(HIT.NSRIF.2015017)

金显吉(1982—)，男，博士，助理研究员，研究方向为电能质量监测，电力系统信息及通信技术;俘为明(1964—)，男，博士，教授，博士生导师，研究方向为电气智能化技术，变电站自动化等;卢 雷(1987—)，男，博士研究生，研究方向为电力系统信息安全;李凤阁(1967—)，女，硕士，高级工程师，研究方向为电力系统自动控制。

俘为明