磁致伸缩对变频器供电永磁电机振动噪声影响

韩雪岩， 张哲， 吴胜男， 陈健

(沈阳工业大学国家稀土永磁电机工程技术中心，辽宁沈阳110870)

磁致伸缩对变频器供电永磁电机振动噪声影响

韩雪岩， 张哲， 吴胜男， 陈健

(沈阳工业大学国家稀土永磁电机工程技术中心，辽宁沈阳110870)

为了研究变频器供电下磁致伸缩现象对电机振动噪声的影响，以一台2.1kW永磁电机为例，应用有限元计算了不同工作频率下的磁场分布和铁心振动位移，在此基础上分析了铁心周围的声场分布，并对该电机的噪声进行了试验研究。通过理论计算与测量结果的比较，验证该计算方法的正确性，为在设计阶段计算永磁电机振动噪声大小、分布和寻求新的降噪措施，提供了理论依据和计算方法。

永磁同步电机;变频器;磁致伸缩;有限元分析;振动噪声

0 引 言

目前对于永磁电机振动噪声的研究通常认为电磁力是电机的主要电磁振动激励源，而忽略了磁致伸缩效应的影响。随着社会经济的发展，人们对电机的振动噪声日益关注，对电机低噪声化也提出了越来越高的要求，因而国内外学者开始逐渐重视电机磁致伸缩效应引起的振动噪声研究。

磁致伸缩效应对电机振动噪声影响的研究正处于起步阶段［1］。一些学者通过测量研究了电工钢的磁致伸缩特性，发现磁致伸缩与磁通密度成非线性关系且不同型号的电工钢磁致伸缩系数不同［2-5］。2002年，比利时Koen Delaere等人对磁致伸缩导致电气装置的振动进行研究，利用磁力藕合有限元方法获得磁致伸缩材料特性。通过研究表明，电磁力和磁致伸缩力通常共同作用改变磁性材料的形状，磁致伸缩力导致材料变形或振动［6］。2008年波兰的Jerzy PODHAJEc KI等学者对无刷直流电机空载时由麦克斯韦力和磁致伸缩引起的振动进行了计算，发现定子铁心中的磁致伸缩会使电机振动的量级增加;由于磁致伸缩引起的电机振动约等于麦克斯韦力产生的振动的20%［7］。2010年，芬兰阿尔托大学Katarzyna Fonteyn等学者对电机定子铁心中磁致伸缩和电磁力引起的振动进行了计算。认为电磁力对电机变形的影响较小［8-9］。但是作者只对电机进行了静态分析，没有考虑电机重量和阻尼的影响。综上所述，磁致伸缩效应对永磁电机影响研究主要集中在振动方面，并未对噪声进行计算。

以一台2.1 kW的永磁电机为例，对变频器供电下的永磁电机进行了磁场分布和振动位移的有限元计算，并进一步分析了电机周围声场的分布情况并通过试验进行验证。该分析方法可在设计阶段实现对电机磁场、振动、及其噪声大小分布的数值化，并为分析新的降噪方法提供理论依据。

1 永磁电机铁心的磁致伸缩测量

为了分析考虑磁致伸缩效应的永磁电机振动噪声，应对无取向各向同性电工钢片进行磁致伸缩特性的测量试验。

将50DW270的无取向硅钢片裁制成100mm× 500mm大小，按照Ic E/TR 62581标准［10］，应用辽宁省现代电工装备理论与共性技术重点试验室的一维磁致伸缩测量系统对该样片进行了测试。得到了不同磁通密度幅值下的磁致伸缩回环，也称为蝴蝶曲线，其中0.6T、1.2T和1.7T测得的蝴蝶曲线如图1(a)所示。为了将测量的磁致伸缩数据应用于电机铁心的形变仿真计算，利用磁通密度幅值与磁致伸缩峰峰值的关系数据，将磁致伸缩回环处理为磁致伸缩单值曲线，进一步通过三次样条插值得到平滑的磁致伸缩单值曲线，如图1(b)所示。

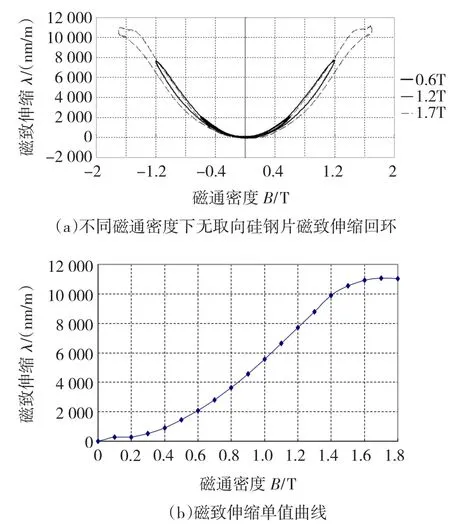
图1 永磁同步电机铁心硅钢磁性测量Fig.1 Magnetic properties measurement of the PMSM core silicon steel

2 考虑磁致伸缩效应的永磁电机振动噪声物理模型

对一台2.1 kW的伺服永磁电机进行了数值计算和试验比较，铁心采用50DW270硅钢片。该电机的主要参数见表1所示。

由于在实际情况下硅钢片并非处于自由状态，为了使建立的模型更接近实际，建立了带有机壳的二维电机模型。还将对电机的周围声场进行计算，故在电机周围建立了一个半径为0.4m的空气外包半圆，电机物理模型如图2所示。

建立模型后，通过多物理场藕合分析软件cOMSOLMultiphysics的前处理功能将模型分为旋转部分、定子、机壳3部分，使用装配体产生两个边界。

图2 二维电机计算区域Fig.2 Calculation area of two-dimensionalmotor

在计算电磁场时选用cOMSOL Multiphysics中Ac/Dc模块中的旋转机械—磁模块，旋转部分和定子接触处的边界设为连续。由于该电机为伺服电机，由变频器供电，为此通过试验测量了该电机不同频率下空载时的电流波形，将其加载到建立的绕组上。最后通过麦克斯韦方程对选中的区域进行求解。

在计算电机的机械振动时，选用cOMSOL Multiphysics中的固体力学模块，定子与机壳接触处的边界设为连续，将电机与地面的接触部分设为固定约束。将定子受到的电磁力根据式(1)添加到定子齿部表面。

单位面积径向电磁力的瞬时值可以表示如下:

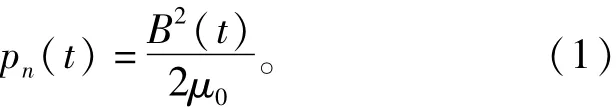
其中:B(t)是电机气隙磁密;μo是真空磁导率。

根据线性压磁方程［2］:

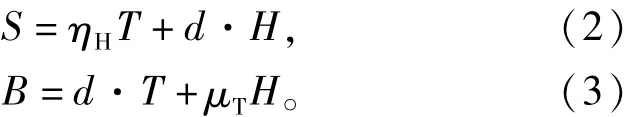
其中:S为应变;ηH为杨氏模量的倒数;T为应力;d为压磁应变系数;H为磁场强度;B为磁通密度;μT为在恒定压力下的磁导率。

通过间接藕合的方式，将磁致伸缩应变项d.H替代成磁致伸缩曲线λ(B)，即可在cOMSOL Multiphysics的固体力学模块计算时考虑磁致伸缩效应。

对电机进行磁—机械藕合分析的主要目的是为了研究铁心磁致伸缩对电机的振动和噪声的影响及如何正确计算永磁电机的噪声大小和分布情况。对计算电机的声场分析域和噪声测试点如图2所示。对于永磁电机，依据计算声学基本原理，电机机壳与空气接触的面独立地辐射噪声，即机壳的外表面振动为声场的源。选用cOMSOL Multiphysics压力声学模块，对电机的声场进行了分析。

选用模块求解域中的方程为

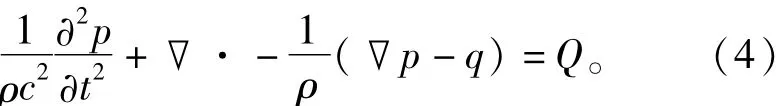
其中:ρ为密度;p为声压;q为可选的偶极子源;Q为外部的源。

根据式(4)可计算得到电机周围声压级的大小和分布。

3 不同供电电流下电机振动噪声计算和试验

3.1 不同供电电流下电机振动计算

通过对电磁力和磁致伸缩效应两种振动力源作用时电机的振动噪声的计算，研究了不同供电电流对永磁电机振动噪声的影响。

对变频器供电下永磁同步电机是否考虑磁致伸缩的瞬态计算结果进行了比较。首先计算了该电机在额定工作频率(fN=266.7 Hz)时电机定子铁心中磁场、机械振动位移的分布。图3所示为0.75 ms时刻电机的磁密分布。

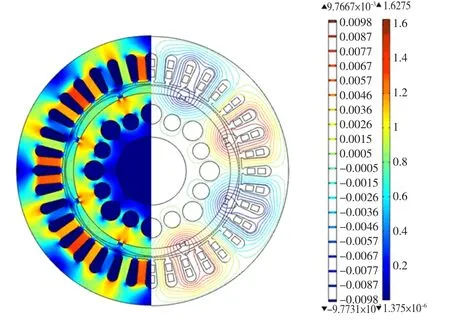
图3 永磁电机分析区域的磁力线和磁密分布Fig.3 The analysis domain and flux density of the PMSM

图4所示为不考虑铁心磁致伸缩效应瞬态解中4个不同时刻(0.75ms，1.5ms，2.25ms，3ms)定子系统变形分布;与此相对应的，图5所示为考虑磁致伸缩与图4中对应的4个不同时刻定子系统变形分布情况。

图4 不考虑铁心磁致伸缩效应瞬定子系统变形分布Fig.4 Deformations from transient with electromagnetic force

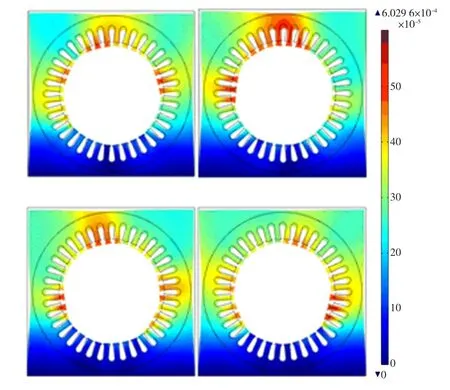
图5 考虑铁心磁致伸缩效应瞬定子系统变形分布Fig.5 Deformations from transient with electromagnetic force and MS

图4和图5右侧表示位移量，单位为mm。为了变形形状视觉化效果，振动变形图的显示比例因子为104。通过图4和图5比较可看出磁致伸缩对电机的振动影响比较明显，考虑磁致伸缩效应时定子的变形量明显大于只有电磁力作用下定子的变形。

此外，还对变频器供电永磁同步电机不同工作频率下，考虑磁致伸缩效应和电磁力共同作用引起的电机振动进行了计算。根据计算得到某时刻不同频率下定子系统变形分布如图6所示。0-4-4

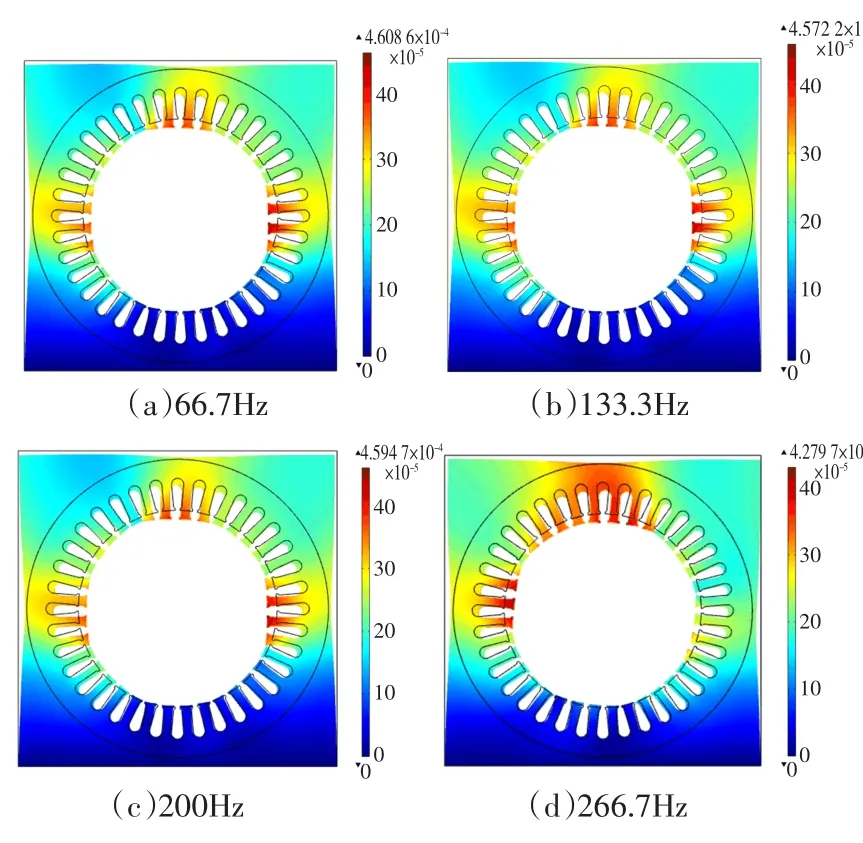
图6 考虑磁致伸缩效应不同频率下定子的变形Fig.6 Deformations from transient with electromagnetic force and MS at different frequency

由图6可见，4种频率下定子系统形变最大值分别为4.608 6×10-4mm、4.572 2×10-4mm、4.594 7×10-4mm、4.279 7×10-4mm，不同工作频率下稳定运行时定子的振动量基本相当，只是振动的频率不同。

选择铁心定子中质点A(如图2所示)，分别计算不同工作频率下电磁力和磁致伸缩共同作用时该点的振动速度、振动加速度，相关信息分别如图7和图8所示。

图7 质点在不同频率下的振动速度比较Fig.7 Vibration velocity of particles under different frequencies

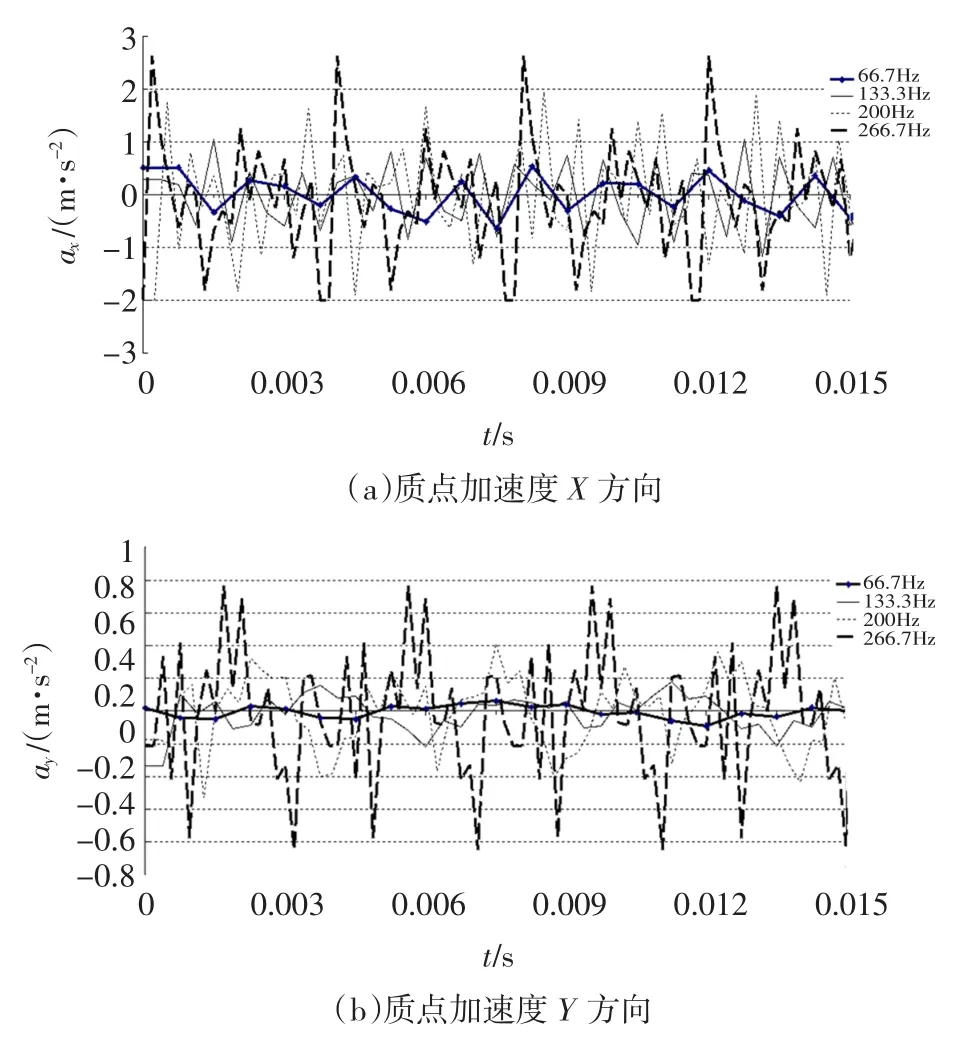
图8 质点在不同频率下的振动加速度比较Fig.8 Vibration acceleration of particles under different frequencies

从图7和图8可以看出，电流频率为66.7、133.3、200、266.7Hz时计算的振动速度在X方向上的最大值分别为0.88×10-4m/s、3.02×10-4m/s、3.26×10-4m/s和3.84×10-4m/s，计算的振动加速度在X方向上的最大值分别为0.48m/s2、1.04 m/ s2、1.96 m/s2和2.67 m/s2，随着频率的变大而增加，在Y方向上也是如此。很明显在高频率状态下质点的振动速度和加速度幅值较大，会产生较大的电磁振动。

3.2 不同供电电流下电机噪声计算和试验验证

由于电机振动位移的数量级较小，很难通过试验对其进行验证。先计算了某时刻电机周围的的声场分布，之后通过试验对比验证计算方法的正确性。

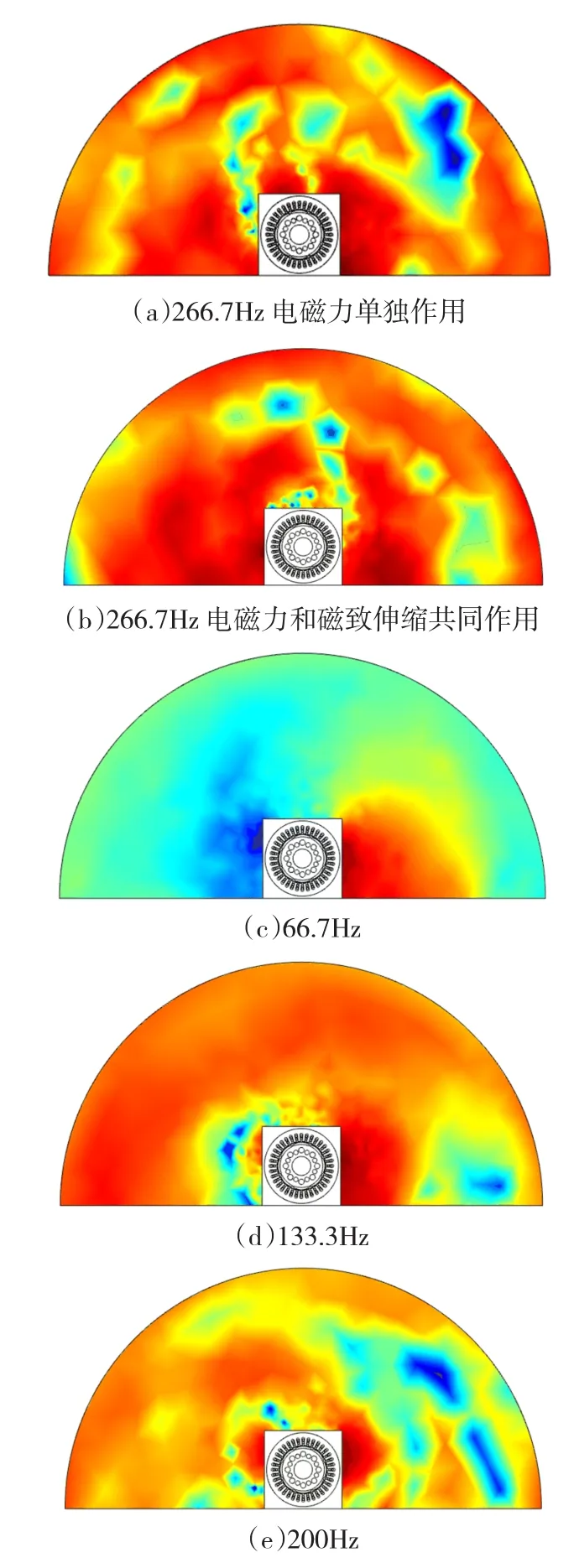
图9 不同频率电流下电机声场分布Fig.9 Sound field distribution of PMSM under different frequency current

某时刻在不同频率电流下的电机声场分布如图9所示。其中，图9(a)为变频器电流为266.7 Hz时电磁力单独作用时电机的声场分布，图9(b)至图9(e)为变频器输出不同频率电流时电磁力和磁致伸缩共同作用时电机的声场分布。

永磁电机的噪声试验在沈阳工业大学国家稀土永磁电机工程技术研究中心消声室内进行。永磁同步电机噪声测量系统由噪声分析仪、数据采集系统、样机组成，如图10所示。

图10 永磁同步电机噪声测量Fig.10 The testing system for PMSM noisemeasurement

通过此系统测量空载运行时2.1 kW永磁同步电机产生的噪声。现将266.7 Hz下电流不同力源引起的噪声计算结果和试验值汇总如表2所示。

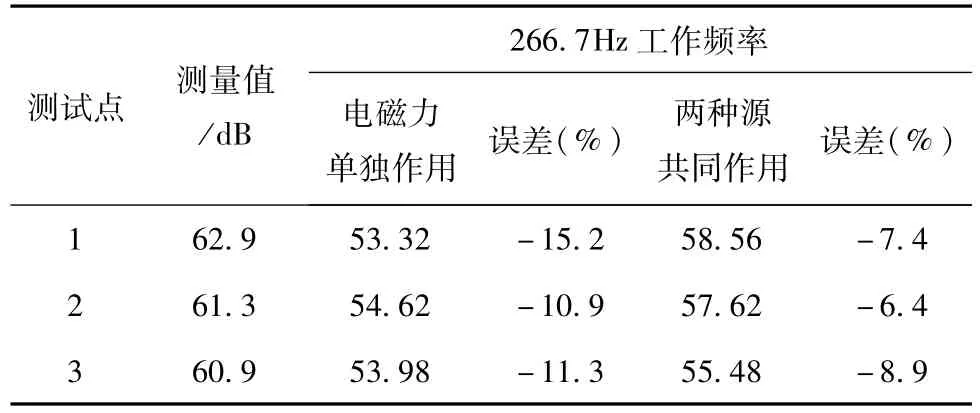
表2 266.7 Hz电流下不同力源引起的噪声Table 2 Noise caused by the different force sourceunder 266.7 Hz current

通过表2中各点的计算值和测量值的比较说明，考虑磁致伸缩效应对永磁电机进行振动噪声的分析值与实际噪声的最大误差为-8.9%，误差范围能够满足工程设计的要求。综上根据电机噪声的分析测量结果，考虑磁致伸缩效应对铁心振动分析结果与测量结果误差远小于不考虑其效应的分析结果，所以，在进行电机设计和预测振动噪声大小时考虑铁心磁致伸缩效应是必要的。

变频器其他频率电流下噪声分析和测量结果如表3所示。

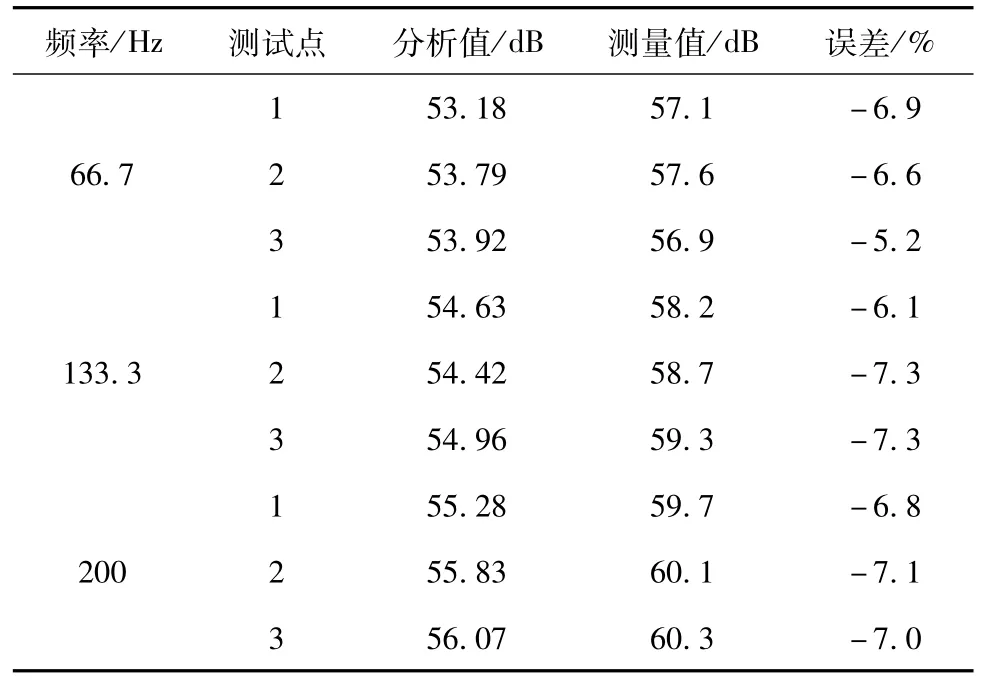
表3 变频器其他频率电流下噪声分析和测量结果Table 3 Results of analysis and measurement of noise under different frequency

从表3可以看出，电机的噪声随着电机通入电流的频率提高而变大。

4 结 论

本文以一台2.1 kW永磁电机为例，应用有限元计算了其不同工作频率下的磁场分布和铁心振动位移，在此基础上分析了铁心周围的声场分布，并对该电机的噪声进行了试验研究，得出以下结论:

1)考虑磁致伸缩效应对永磁电机进行振动噪声的分析值与实际噪声的大小基本相等，比单独考虑电磁力时更接近试验值。所以，在进行电机设计和预测振动噪声大小时考虑铁心磁致伸缩效应是必要的。

2)通过计算和试验发现，电机的振动噪声随着变频器接入电流频率的提高而变大，计算误差的来源可能是电机的机械振动噪声影响。

3)经过声场分析将电机周围声压级大小和分布可视化，可为设计阶段预测电机噪声大小和分布具提供有效分析方法，为进一步分析验证降低电机振动噪声新方法新措施提供理论依据和计算方法。

［1］ Anouar Belahcen.Vibrations of rotating electricalmachines due to magnetomechanical coupling and magnetostriction［J］.IEEE Transactions on Magnetics，2006，42(4):971-974.

［2］ 冯大军，朱业超，黄璞，等.无取向硅钢片磁致伸缩特性的试验研究［J］.武汉工程职业技术学院学报，2009，2(3):13-15. FENG Dajun，ZHU Yechao，HUANG Pu，et al.Laboratorial study on magnetostriction characteristics of non-oriented silicon steel sheet［J］.Journal ofWuhan Engineering Institute，2009，2(3):13 -15.

［3］ 张艳丽，孙小光，谢德馨，等.无取向电工钢片磁致伸缩特性测量与模拟［J］.电工技术学报，2013，28(11):176-181. ZHANG Yanli，SUN Xiaoguang，XIE Dexin，et al.Measurement and simulation ofmagnetostrictive properties for non-grain oriented electrical steel sheet［J］.Transactions of china Electrotechnical Society，2013，28(11):176-181.

［4］ Sakda Somkun，Anthony J.Moses，Philip I.Anderson，et al.Quantification of magnetostriction for analysis of vibration of electrical machine cores［c］//The45th International Universities Power Engineering conference(UPEc)，Aug.31-Sept.3，UK，2010:1 -6.

［5］ Sakda Somkun，Anthony J.Moses，Philip I.Anderson.Mechanical resonance in non-oriented electrical steels induced bymagnetostriction under PWM voltage excitation［J］.IEEE Transactions on Magnetics，2008，44(11):4062-4065.

［6］ Koen Delaere，Ward Heylen，Ronnie Belmans，et al.comparison of inductionmachine stator vibration spectra induced by reluctance forces and magnetostriction［J］.IEEE Transacions on Magnetics，2002，38(2):969-972.

［7］ Jerzy PODHAJEc KI，Adrian MLOT，Mariusz KORKOSZ.comparison vibration due to Maxwell forces andmagnetostriction in BLDc motor-dynamic analysis［J］.Prace Naukowe Instytutu Maszyn，Napedów i Pomiarów Elektrycznych Politechniki Wroclawskiej，2008，62(28):325-330.

［8］ Katarzyna Fonteyn，Anouar Belahcen，Reijo Kouhia.FEM for directly coupled magneto-mechanical phenomena in electrical machines［J］.IEEE Transactions on Magnetics，2010，46(8):2923 -2926.

［9］ Katarzyna Fonteyn，Anouar Belahcen，Reijo Kouhia.contribution of Maxwell stress in air on the deformations of induction machines［J］.Journal of Electrical Engineering&Technology，2012，7 (3):336-341.

［10］ IEc/TR 62581，Electrical Steel-Methods of Measurement of the Magnetostriction characteristicsby Meansof Single Sheetand Epstein Test Specimens［S］.

(编辑:刘素菊)

Research on vibration and noise of permanent magnetmotor caused by magnetostriction effects under inverter power supply

HAN Xue-yan， ZHANG Zhe， WU Sheng-nan， cHEN Jian
(National Engineering Research center for REPM Electrical Machines，Shenyang University of Technology，Shenyang 110870，china)

In order to develop the influences of magnetostrictive phenomenon on vibration and noise of motor under inverter power supply，taking a 2.1 kW permanentmagnet synchronousmotor(PMSM)as an example，themagnetic flux and vibration of themotor were calculated under differentworking frequency. On the basis of the vibration calculation，acoustic field around the motor was analyzed.And then，the noise of themotor was experimented.Through the comparison of theoretical calculation and measurement results，the validity of the proposedmethod was verified.Furthermore，thismethod which could help predict the noise level in permanentmagnetmotor design step and seek new denoise methods has great potential in future application.

permanent magnetmotors;frequency converter;magnetostriction;finite element analysis;vibration and noise

10.15938/j.emc.2015.04.001

TM 351

A

1007-449X(2015)04-0001-06

2014-07-11

国家科技支撑计划项目(2013BAE08B00);国家自然科学基金(51307111);辽宁省教育厅科学技术研究项目(L2013049)

韩雪岩(1979—)，女，博士，副教授，研究方向为特种电机及其控制技术;张 哲(1988—)，男，硕士研究生，研究方向为永磁电机振动噪声;吴胜男(1985—)，女，博士研究生，研究方向为永磁电机振动噪声;陈 健(1982—)，男，硕士，研究方向为永磁电机振动噪声。

韩雪岩