VMI模式下供应链物流成本核算及利益分配模型—面向汽车零部件市场

赵 琨，刘金虎

（北京物资学院 物流学院，北京 101149）

VMI模式下供应链物流成本核算及利益分配模型—面向汽车零部件市场

赵 琨，刘金虎

（北京物资学院 物流学院，北京 101149）

针对北京现代汽车制造有限公司零部件物流，提出应用VMI-TPL集成模式降低供应链整体物流成本的方案。结合定性分析和定量分析，构建实施VMI-TPL集成模式前后，参与供应链各方的物流成本模型，进而得出供应链物流总成本变化模型。通过对实际影响因素的筛选，设定关键参数构建模型，通过定量计算验证了实施VMI-TPL集成模式可使供应链整体物流成本降低的结论。利用Shapley值法建立了参与供应链各方的利益分配模型，得出各方都相对满意的分配方案，为VMI-TPL集成模式的实行奠定理论基础。

VMI-TPL；汽车物流；成本核算；利益分配

1 引言

供应商管理库存（Vendor Managed Inventory,VMI）是一种供应链集成化运作的决策代理模式，可以通过合理的库存管理和补货策略减少供应链整体的库存水平，使供应链整体效益得到优化。但该模式对供应商的物流水平要求较高，由供应商单独实现VMI会分散其资源和精力到非核心业务上面，同时也难以达到所设定的水平，甚至可能拖累主营业务的经营。而在汽车零部件物流领域中，早已成功运用专业的第三方物流，汽车厂商将自己并不擅长的物流业务外包给第三方物流公司，由其提供专业的物流服务，既提升了物流服务水平，又集中了资源和精力。因此VMI在汽车零部件物流领域中实施，借助第三方物流可以有效弥补自身的先天不足，发挥最大效益。

第三方物流（Third Part Logistics,TPL）是相对自营物流而言，由供方与需方以外的第三方物流企业提供物流服务的业务模式，一般把提供第三方物流服务的公司成为第三方物流公司。第三方物流公司通过为客户提供仓储、运输、流通加工、配送、信息数据处理、物流方案设计及其他增值服务来获取利益，既不直接参与商品的买卖，也不拥有货权。

VMI-TPL模式是指供应商借助第三方物流的专业优势，弥补自身物流服务水平的不足，为实施VMI模式创造条件。VMI模式的实施对供应商的物流服务水平要求较高，需要具备一定的物流规划及物流系统设计能力，通过不断调整物流系统的各项参数达到VMI持续改进的效果。而供应商一般只具备处理简单的仓储、运输、流通加工等业务的能力，物流业务并不是其主营业务，这也是制约VMI模式在全行业实行的关键。因此，有第三方物流参与的VMI-TPL模式有效地弥补了VMI模式的先天缺陷。

本文希望通过建立面向汽车零部件供应市场的供应链物流成本模型，研究VMI模式在该领域推行所产生的经济效益，进而建立由一个供应商、一个第三方物流公司和一个主机厂构成的单级供应链实施VMI的利益分配模型，得出具有代表性的分配方案。合理的利益分配方案可以很大程度上促进供应商主动实施VMI，从而促使供应链整体效益趋向最大化。VMI的最大作用不是单个参与者实现成本降低，而在于其对整条供应链的影响，寻求供应链整体效益最优才是最终目标。利益分配的研究可以提高供应商对实施VMI的积极性，而准确的成本核算是利益分配的基础，因此本文研究供应链中各个参与者的物流成本核算与利益分配具有现实意义。

2 国内外研究现状

VMI是一种供应链集成化运作的决策代理模式，以双方成本最低为目标，在一个共同框架协议下把用户库存决策权代理给供应商，由供应商代理分销商或批发商行使库存决策权力，并通过对该框架协议经常性监督和修正使库存得到持续改进。VMI概念最早是由Magee（1958）探讨货权的最佳归属时提出的，但真正应用到实践中是在20世纪80年代末沃尔玛和宝洁公司的成功合作，通过实践验证了VMI模式在降低供应链整体库存及提高物流服务水平方面的作用。此后VMI模式逐渐进入学术界的视野，大量文献相继涌现。

周阳[1]（2012）研究了针对单一品种的“单供应商、多分销商”物流配送网络，以寻求最优的库存补货策略及运输配送决策，构建了VMI模式下库存与运输集成化模型。崔文全[2]（2014）研究了VMI模式在企业中的应用，但仅局限于面向供应商及零售商的供应链，并未涉及生产企业。宣杰[3]（2014）等研究了制造型企业如何实施VMI模式，从确定VMI物料、筛选合格供应商、选择实施形式、实施策略等方面构建了VMI的体系框架，但并未涉及制造型企业实施VMI模式前后的直接利益变化，缺少说服力。谭洁[4]（2014）等研究了库存成本视角的供应链VMI利益分配问题，应用价格契约和Stackelberg博弈模型建立了零售商强势情况下供需双方利益分配模型，局限在于没有推广到涉及第三方物流的三方利益分配问题。夏晗[5]（2014）研究了具有单一供应商及单一销售商的供应链系统协调机制，通过模型分析了供应商及销售商的利润变化情况。

Zahra Lotfi[6]（2015）等研究了信息共享对供应链管理的重要影响，得出加强企业间信息共享可以提高供应链的竞争性。Seyed Taghi[7]（2015）等研究了多供应商多零售商供应链随机需求和不平等的补货周期的供应商管理库存。Arqum Mateen[8]（2015）等研究了单供应商多零售商供应链的供应商管理库存。Javad Sadeghi[9]（2015）等研究了VMI模式下供应链成本的优化。

王道平[10]（2011）等基于传统的EOQ模型，在充分考虑运输成本和安全库存量的条件下，构建了TPL模式下的VMI库存模型，论证了新模型降低了供应商的库存成本和物流成本，但随着订货成本的增加，库存和物流相关成本呈上升趋势，但是他仅考虑了不允许缺货的情况，并未拓展到允许缺货，有缺货成本及补货有延时的情况。徐静[11]（2012）研究了VMI-TPL模式下的库存运输集成问题（Inventory Routing Problem, IRP）。黄活泼[12]（2012）研究了面向汽车制造业零部件供应商的第三方物流参与下的VMI服务模式，并基于数学模型对第三方物流开展VMI服务的预期增值效益进行分析，具体包括对供应链总体物流成本、供应商利润及制造商利润的变化情况，但没有涉及到利益分配问题。李正[13]（2014）对有第三方物流参与的VMI进行了利润分析，对比了有第三方物流参与的新型VMI模型和没有第三方物流参与的传统VMI模型。戴君[14]（2015）等构造了面向生产型企业，TPL拥有库存决策权且不允许缺货的VMI模型，将VMI模式推广到了生产企业。常莎莎[15]（2015）等针对第三方物流实施VMI模式，研究了如何在满足客户对货物送达时间窗要求的前提下，使得车辆综合利用率最优的问题，以容积积载率、重量积载率、时间积载率为优化目标，建立了带时间窗限制的多车多品种货物配装问题的数学模型。

3 供应链成本核算模型

谭杰[4]等研究了针对供应商-零售商的供应链库存成本模型，在该模型中，运输成本、库存维持成本及订货成本被考虑其中，运用EOQ模型，计算得出零售商的经济订货批量。由于实施了VMI模式，库存决策权由供应商掌握，因此该经济订货批量就是供应商的最优补货批量，进而得出供应链的库存成本。该模型是面对供应商-零售商订单推动式的供应链，因此可以做到恒定订货批量；而本文所需的模型针对汽车制造业零部件供应领域，属于供应商-制造商需求拉动式的供应链，采用EOQ模型的恒定订货批量不符合实际情况，且该文并未引入第三方物流。

本文从该文中汲取分类计算的思想，将物流成本细化为运输成本、仓储成本和流通加工成本，基本涵盖物流成本的主要组成部分，并在供应链中加入第三方物流，引入距离参数，将制造商周边的供应商或第三方物流公司仓库考虑其中，各个成员的物流成本分别构建模型，进而得出供应链整体物流成本模型。模型前提是采用恒定周期采购的方式，计算单个周期内的物流成本，更贴合汽车制造业的实际情况。

假设：

（1）不考虑缺货情况及缺货成本；

（2）设定只有一个供应商、一个第三方物流公司和一个汽车制造商的供应链；

（3）库存决策权由第三方物流公司和供应商共同掌控，第三方物流公司拥有提议权，供应商拥有决策权，供应商产成品的所有物流活动均交由第三方物流公司运营；

（4）汽车生产商将生产计划等信息提前一周告知供应商和第三方物流公司；

（5）以一个周期为节点计算物流成本。

参数设定：

CS：供应商单位时间内存储成本；

Cm：制造商单位时间存储成本；

Cl：TPL单位时间内存储成本；

Q：制造商订货批量；

T：订货周期；

Ct：运输成本；

Cll：TPL单位产品物流处理成本；

λ：库存放大系数，且1≤λ≤2；

α：供应商物流成本放大系数，且α≥1；

NS：供应商安全库存；

L1：供应商到制造商周边的RDC的距离，L1≥500km；

L2：RDC到制造商的距离，L2≤10km。

3.1 实施VMI-TPL模式之前物流成本模型

供应商物流成本分为库存成本、运输成本和物流加工处理成本，这三项成本对应的物流活动均由供应商自营，只计算成本。为保证及时供货，供应商一般设定λ倍的库存放大系数，汽车制造商提前一个周期向供应商下达订单，在该周期内供应商生产出订货量放大λ倍数量的零部件，预留紧急订单的货量。生产之后，在下一周期将订单货物运送到制造商处，剩余的λ-1订货量的零部件划归安全库存NS。

因此，每一个周期T内，都有订货量Q的零部件在仓库内存储，同时有(λ-1)Q的货物会存放两个周期，因此供应商库存成本为

供应商物流成本模型：

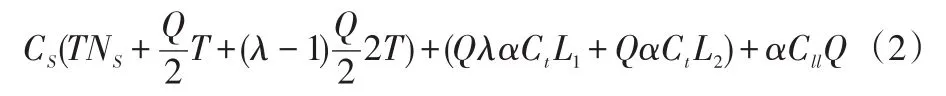
其中，第一项是库存成本，第二项是运输成本，第三项是物流加工处理成本。

制造商物流成本只有库存成本,其模型为：

供应链总成本模型如下：

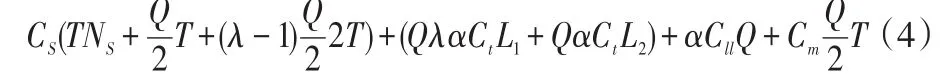
3.2 实施VMI-TPL模式之后物流成本模型

供应商由于确切掌握制造商的生产计划、消耗速度、销售数量等信息，最理想的情况下，供应商可以逐步减小库存放大系数，直至不放大，即λ=1，产品生产出来在仓库存放一个周期T后，由第三方物流公司负责之后的运输配送、流通加工等活动，供应商支付给物流公司一定的物流费用，以实际处理量来计算，此时供应商的物流成本包括库存成本和支付给第三方物流公司的物流费用。供应商物流成本模型为：

TPL物流成本：

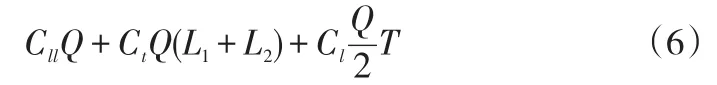
第一项为物流加工处理成本，第二项为运输成本，第三项为库存成本。

制造商由于实施VMI，库存压力转移到上游供应商，因此库存成本变为零。

供应链总成本：

VMI实施后，供应商物流成本变化为（5）-（2）：

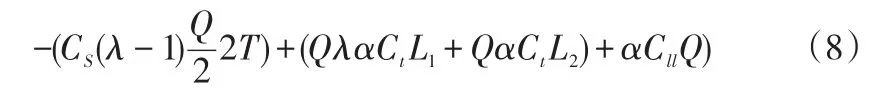
第三方物流公司物流成本变化为式（6）。制造商物流成本变化为：

供应链总成本变化为：

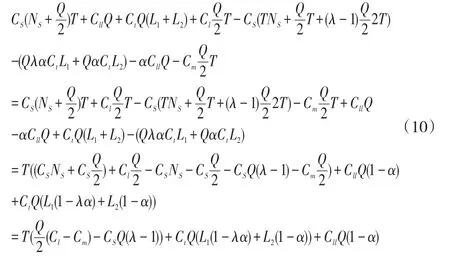
式（10）中第一项为供应链仓储总成本变化，第二项为供应链流通加工总成本变化，第三项为供应链运输总成本变化。

由于第三方物流的专业性和物流作业的规模效益，我们默认在各环节物流作业成本的比较中，第三方物流公司均比供应商和制造商低。在此前提下，式（10）中第一项，TPL的单位时间内存储成本Cl低于制造的单位时间内存储成本Cm，1≤λ＜2，所以Cl-Cm＜0，λ-1＞0，因此第一项小于零，即实施VMI后供应链仓储总成本有所降低；式（10）中第二项，由于(1-λα)＜0，(1-α)＜0，因此第二项小于零，即实施VMI后供应链流通加工总成本有所降低；式（10）中第三项，1≤α＜2，(1-α)＜0，因此第三项小于零，即实施VMI后供应链的运输总成本有所降低。

综上所述，在汽车零部件供应物流领域，应用VMI模式可以有效减少供应链总物流成本。

4 供应链利益分配模型

Shapley值法是Shapley L S在1953年发表的解决N个成员合作对策问题收益分配的数学方法。当n个成员从事某项经济活动时，对于他们之中若干成员组合的每一种合作参与形式，都会获得一定的效益，当成员之间的利益活动为非竞争性时，合作中成员数量的增加不会引起收益的减少，这样，全体n个成员的合作将带来最大收益，Shapley值法是分配这个最大收益的一种方案。供应链上各企业通过核心能力的优化调整，实现风险共担、资源共享，可以有效地分担风险，降低成本，促进企业创新，从而得到比加入供应链前更高的利润。供应链上企业都是独立经营的经济实体，以各自的利润最大化为目标，因此对每个企业而言，使整条供应链增加利润是该企业可以加入供应链的前提；加入供应链后，该企业所获得的利润不少于加入供应链前能获得的利润是维持供应链正常运转的保证。因此，供应链各合作伙伴间的利益分配问题可以看作是多人合作对策的利益分配问题，可以用Shapley值法求解,其定义如下：

设集合I={1 ,2,…,xi}，如果对于I的任一子集s（表示n个人集合中的任一组合）都对应着不同的v(s)，并且满足：

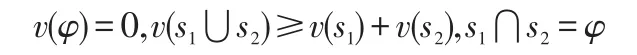
那么称[I,v]为n人合作对策。用xi表示I的成员i从合作中最大收益v(l)所获得的收益。当满足：

则称x=(x1,x2,…,xn)为n人合作对策下的其中一个分配。

ϕi(v)=0表示在I的合作方式下运用Shapley值法所计算的第i个成员所得的分配利益，则在I的合作方式下各个成员所得利益的Shapley值为：

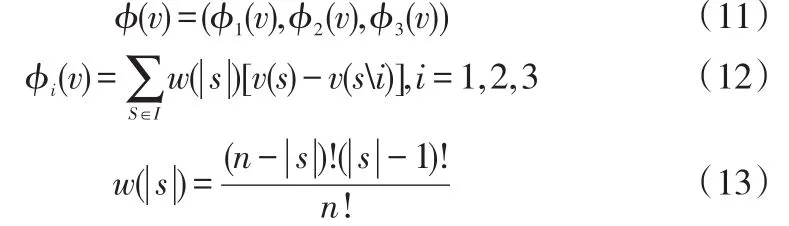
其中，|s|是子集s中的元素个数，w(|s|)是加权因子。v(s)是在s的合作方式下的收益，v(si)是s去除i后得到的收益。

李晓晓[16]等研究了Shapley值法分配引入VMI-TPL模式的供应链收益问题，此处的收益为营业收益。由于该文章的研究重点是利益分配问题，在利益核算方面较为简单，构建的模型及算例均以简单的字母参数和数值直接代入，涉及的物流成本相关内容较少。

在本文中，Shapley值法所提到的收益是指实施VMI-TPL模式后，供应链物流整体成本的减少量，零部件供应商、第三方物流公司和汽车制造商对减少的物流成本进行分配，且利益分配模型建立在第三章物流成本核算的基础上，对上文计算得出的物流成本进行分配，衔接性更好。

下面构建本文的供应链Shapley值法模型。

（1）s={1}或{2}或{3}，即供应商或第三方物流公司或制造商。此时供应链中的各个成员独立经营决策，只关注自身利益不求合作，无任何成员参与的供应链也就没有任何收益的增加，所以：

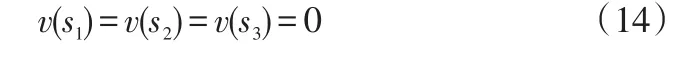
（2）s12={1 ,2}，s23={2 ,3}或s13={1 ,3}。以上合作是供应链成员中任意两个之间的合作。v(s)等于供应链实施合作方式后较实施前的成本减少值，所以：

（3）s=I={1,2,3}。这是代表供应链实施VMI-TPL的集成模式。v(s)等于供应链实施合作方式后较实施合作方式前的成本减少值，所以：

（4）采用该方法分别计算供应商、第三方物流公司和制造商分得的利益，具体计算方法如下：

①供应商利益分配

表1 供应商利益分配机制的相关参数表

这里的IS指供应商参与合作的I的所有子集的集合。

②第三方物流公司利益分配

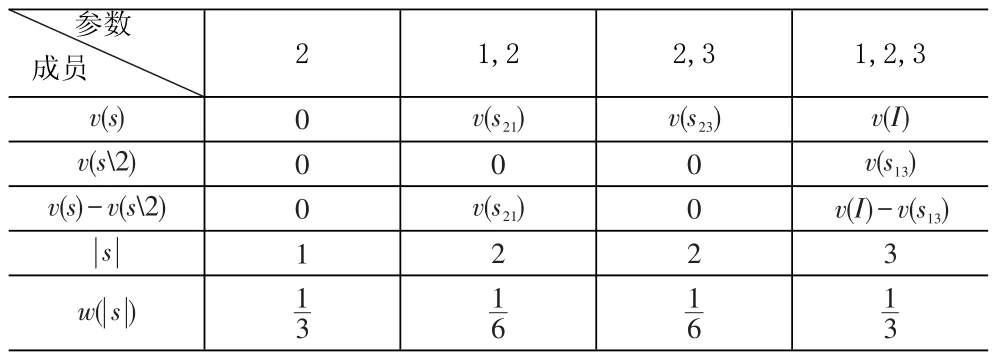
表2 第三方物流公司利益分配机制的相关参数表

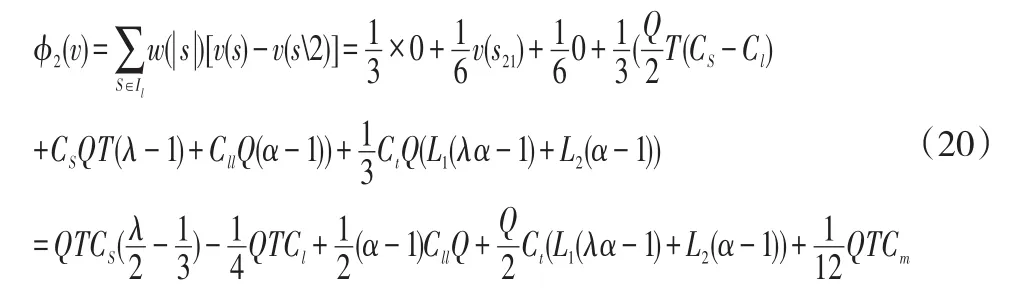
这里的Il指第三方物流公司参与合作的I的所有子集的集合。

③制造商利益分配

表3 制造商利益分配机制的相关参数表

这里供应链共有3个成员，因此将参数代入得：

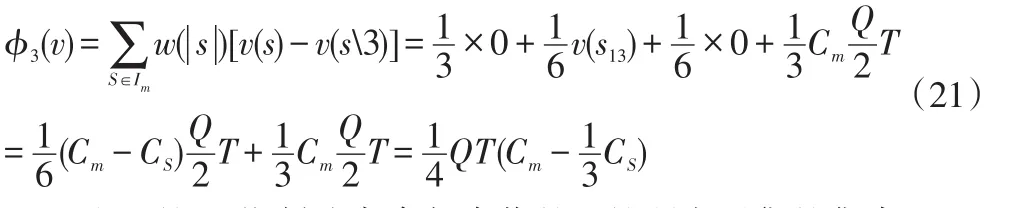
这里的Im指制造商参与合作的I的所有子集的集合。

5 算例分析

北京现代汽车制造有限公司在北京拥有3个制造厂，总产能110万台，平均每周约为21 154台。假设某零部件供应商可以供应北京现代全车型的一种零部件，即供应商平均每周生产供应21 154套零部件，为便于计算，只取平均值作为代表性数值。北京现代提前一周将生产计划等信息告知供应商及第三方物流公司，供应商根据预测的批量进行生产，之后的物流作业交由第三方物流公司负责。

一般情况下，供应商会设定10%左右的库存放大系数，即每批次生产批量放大系数λ=1.1。由于第三方物流公司在物流业务方面的优势，设定第三方物流公司的物流作业成本放大α=2倍为供应商和制造商的物流作业成本；由于制造商的土地资源有限，人员工资、设备购置费用及管理成本平均到每个零部件上更高，因此设定仓储成本Cm＞CS＞Cl，具体数值为Cm=2Cl，CS=1.1Cl，具体输入参数见表4。

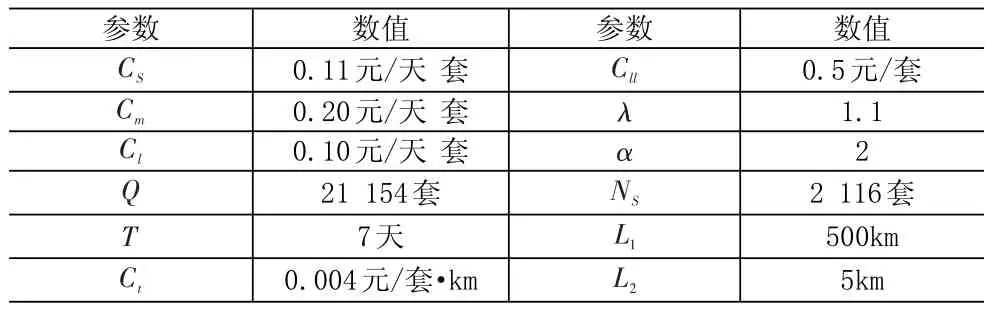
表4 输入参数

将表4数据带入式（10）得，供应链实施VMI-TPL模式一个周期内物流总成本变化：

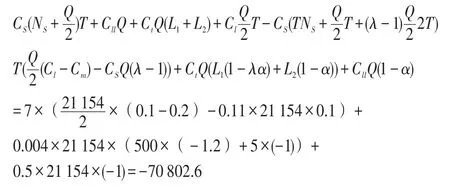
（1）供应商分得收益

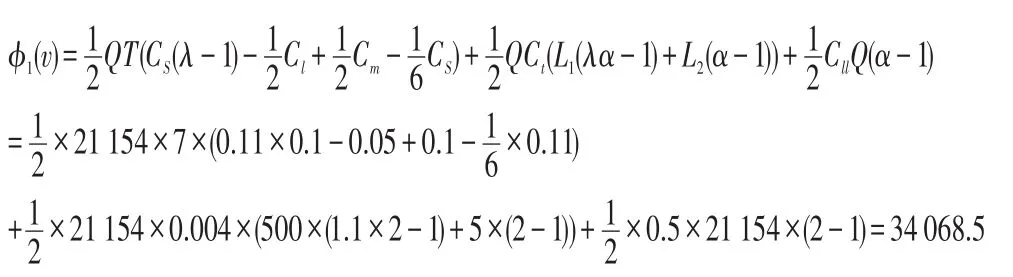
（2）第三方物流公司分得收益

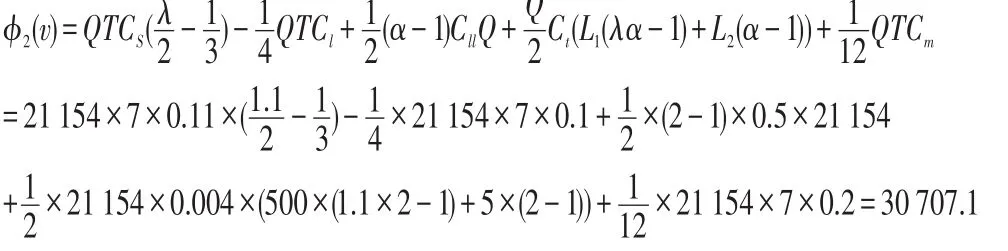
（3）制造商分得收益

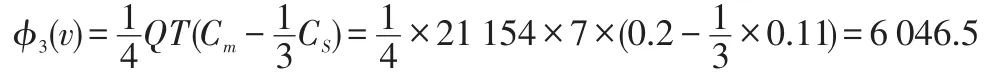
使用Shapley值法计算得出的总收益为34 068.5+ 30 707.1+6 046.4=70 822元，而供应链降低的物流总成本为70 802.6元，误差为0.03%，证明该收益分配方案具备可行性。

以上收益为参与供应链的三方成员最终应获得的净收益，将参数分别代入式（6）、（8）、（9）三方的成本变化值如下：

（1）供应商物流成本变化：

（2）第三方物流公司物流成本变化：

（3）制造商物流成本变化：

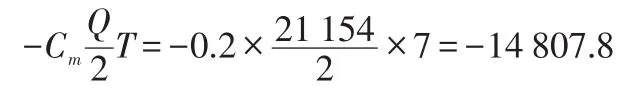
因此制造商每周期支付给供应商订货费用：

14 807.8-6 046.4=8 761.4元

供应商每周期支付给第三方物流公司物流服务费用：

116 706.7-34 068.5+8 761.4=91 399.6元

6 结论

汽车行业是国民经济的支柱产业，其发展带动了橡胶、钢铁、电子、机械等一系列周边产业的发展，拉动经济增长，促进就业，对国民经济贡献极大，作为配套服务的汽车物流服务因此也越来越受到关注。由于发展水平的原因，我国汽车制造商的物流成本普遍高于国际水平，研究降低汽车物流成本的问题具有实际意义。

本文研究主要针对北京现代的零部件物流运营模式，探究在第三方物流的参与下，VMI-TPL模式对各成员物流成本和供应链整体物流成本的影响，通过建立物流成本模型进行定量分析，得出实施VMI-TPL模式可使供应链整体物流成本下降，即可使利益增加；之后采用Shapley值法对收益进行分配，得出各方易于接受的分配方案；最后通过北京现代的实际案例对模型及结论进行验证，证实方法可行。

[1]周阳.VMI模式下库存与运输集成化模型机算法研究[D].长沙:中南大学,2012.

[2]崔文全.VMI模式在企业中的运用研究[J].郑州航空工业管理学院学报,2014,32(3):82-87.

[3]宣杰,毕英英,王静.制造型企业实施VMI模式的体系构建[J].物流工程与管理,2014,36(9):130-132.

[4]谭洁,郑齐,林强.基于库存成本视角的供应链VMI利益分配[J].武汉理工大学学报(信息与管理工程版),2014,36(4):523-527.

[5]夏晗.VMI模式下基于批量生产的供应链协调研究[EB/OL].http:// www.cnki.net/kcms/detail/11.3443.F.20141112.1519.261.html,2014-11-12.

[6]Zahra Lotfi,Muriati Mukhtar,Shahnorbanun Sahran,Ali Taei Zadeh.Information Sharing in Supply Chain Management[J].Procedia Techology, 2013,(11):298-304.

[7]Arqum Mateen，Ashis Kumar Chatterjee.Vendor managed inventory for single-vendor multi-retailer supply chains[J].Decision Support Systems,2015,70:31-41.

[8]Poorbagheri T.Vendor managed inventory of a multiple-vendor multiple-retailer supply chain with stochastic demand and unequal replenishment cycle times[EB/OL].http://www.researchgate.net/publication/ 271854823.

[9]Javad Sadeghi,Mahziar Taghizadeh,Ahamd Sadeghi,Reza Jahangard, Reza Tavakkoli-Moghaddam.Optimizing a vendor managed inventory (VMI)model considering delivering cost in a three-echelon supply chain using two tuned-parameter meta-heuristics[J].International Journal of System Assurance Engineering and Management,2014,(4):1-11.

[10]王道平,等.第三方物流参与供应商管理库存模型[J].工业工程, 2011,14(5):1-7.

[11]徐静.基于VMI-TPL模式的库存运输集成模型和算法研究[D].长春:吉林大学,2012.

[12]黄活泼.基于第三方物流的VMI服务模式研究—面向汽车制造业零部件供应商[D].广州:华南理工大学,2012.

[13]李正.第三方物流参与的供应商管理库存利润分析[J].物流技术，2014,33(6):272-275.

[14]戴君,等.基于第三方物流的生产型企业的VMI问题研究[J].现代管理科学,2015,(1):106-108.

[15]常莎莎,等.第三方物流实施VMI配送优化的研究[J].经营与管理, 2015,(3):126-130.

[16]李晓晓,等.引入TPL的VMI集成模式的利益分配研究[J].物流技术, 2014,33(8):319-321.

Logistics Cost Accounting and Benefit Allocation Model of Automobile Spare Parts Supply Chain under VMI Mode

Zhao Kun,Liu Jinhu
(School of Logistics,Beijing Wuzi University,Beijing 101149,China)

In this paper,in view of the spare parts logistics process of the Beijing HYUNDAI Automobile Manufacture Co.,Ltd.,we proposed to use the integrated VMI-TPL mode to reduce the overall logistics cost of the supply chain,then built the logistics cost model of the supply chain participants both before and after the implementation of the integrated VMI-TPL mode to derive the total logistics cost change model of the supply chain.Next through screening the actual influence factors and defining the key parameters,we built the corresponding model to verify the conclusion that the implementation of the integrated VMI-TPL mode could reduce the overall logistics cost of the supply chain.At the end,we used the Shapley value method to build the benefit allocation model of the supply chain participants

VMI-TPL;automobile logistics;cost accounting;benefit allocation

F570；F252

A

1005-152X(2015)10-0213-05

2015-08-25

北京高等学校青年英才计划项目（Beijing Higher Education Young Elite Teacher Project）；国家自然科学基金资助项目（11271361）

赵琨，北京物资学院物流学院讲师，博士，研究方向：最优化、数据挖掘、支持向量机。

10.3969/j.issn.1005-152X.2015.10.057