物流能力随机条件下的LSSC任务分配模型及算法

吴晓研，路世昌，刘忠敏

（1.吉林师范大学 管理学院，吉林 四平 136000；2.辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 123000）

物流能力随机条件下的LSSC任务分配模型及算法

吴晓研1,2，路世昌2，刘忠敏1

（1.吉林师范大学 管理学院，吉林 四平 136000；2.辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 123000）

实际物流运作过程中，功能型物流提供商的物流能力具有随机性。考虑FLSP物流能力的随机性，建立了物流服务供应链订单分配模型，并给出了模型的求解方法，最后进行了算例分析。

物流能力；随机条件；物流服务供应链；订单分配；遗传算法

1 引言

物流服务供应链（Logistics Service Supply Chain,LSSC）是适应物流发展要求而出现的一种新型供应链模式。LSSC以物流服务集成商（LSI）为核心，通过与功能型物流服务提供商（FLSP）合作，共同完成产品的物流运作。物流服务供应链本质上是一条能力链，由于其服务的无形性、不可储存性和顾客参与性等特点，更具有动态性和不确定性。LSSC任何一个节点企业或环节出现差错，都会波及其他节点企业或环节，甚至整个供应链[1]。作为物流服务供应链中的一环，供应商的选择对物流供应链的发展极其重要。物流供应商合作伙伴的选择及物流任务分配的合理性直接影响物流运作的稳定性与可靠性。物流服务集成商根据其客户群体的需求与自身供应能力的分析，与各个专业化功能型物流服务提供商建立外购关系，如何选择外购的物流供应商及最优分配任务量成为物流服务供应链研究的关键。

对于产品供应链，可靠性已成为合作伙伴选择的一个重要因素[2-3]，对于物流供应链，已有学者认识到物流运作可靠度的重要性，但相关文献并不多见。刘伟华、季建华、周乐[4]（2008）研究了不确定需求情况下，物流服务集成商面对多个功能物流服务提供商时如何进行订单任务分配的问题，并综合考虑了成本、满意度、惩罚强度和能力匹配等因素，研究表明，物流服务集成商的关系成本系数与物流提供商的总体满意度和惩罚强度有密切关系。张德海等[5]（2009）提出基于可靠度分配的物流服务能力优化模型，研究LSSC可靠性、成本及服务能力之间的协调。姜意扬等[6]（2011）建立了基于物流供应商现有手头订单、物流能力可获得性、配送效率、缺损率与成本的供应商选择与订单分配组合优化模型，并进行了算例分析。陈玉镇、赵一飞[7]（2012）在综合考虑物流服务供应商的成本、服务质量和满意度的基础上，构建了物流服务供应链物流任务分配的多目标规划模型。程建刚、李从东（2009）[8]提出了一种多目标混合整数规划模型来优化物流服务供应链网络，综合考虑了服务质量、服务能力、交付时间等因素。李珊珊[9]（2014）针对物流服务供应链订单分配问题中，物流服务集成商通常会按照所分配的订单价值向分包商收取一定比例交易费用的特点，构建了新的物流服务供应链订单分配优化混合整数规划模型，并设计了相应的遗传算法。范琛等[10]（2014）提出一个多期多任务的多目标动态整数规划模型，通过引入方案锁定期和带服务质量目标控制机制，进一步给出了存在信息更新的多次订单分配规划模型。

关于物流供应商合作伙伴选择问题的研究，上述文献综合考虑了成本、满意度、可靠性、物流能力等因素，但并没有对FLSP物流供应能力的随机性进行假定。由于供应链通常只是复杂供应网络的一部分[11]，功能型服务提供商可能不只是为一个集成商服务。因此，在现实物流运作中，FLSP存在与多个物流集成商合作的情况，在完成某一集成商订单任务的过程中，其可供使用的物流能力是不确定的。因此，本文假定集成商在进行任务分配时，FLSP的可用物流能力服从一定的概率分布，从而FLSP完成既定任务量的物流运作的可靠性也服从一定的概率分布。

2 物流服务供应链任务分配模型

设集成商需将一任务量为D的物流任务外包给若干个FLSP完成，现有多个FLSP对该任务进行竞标。由于各投标企业可靠度与成本各不相同，需要综合考虑成本、可靠性及满意度等因素进行合理分配。

设共有m个物流供应商企业参与竞标，wi为第i个FLSP的单位能力竞标价格，i=1,2,…,m。物流集成商的成本不仅包括随订单变化的配送费用，还包括与供应商建立与维持合作关系的固定成本。设集成商与所有FLSP合作的固定成本相同，均为 f。 xi表示分配给第 i个FLSP的任务量，0≤xi≤D。故完成该物流任务的总成本可表示为其中yi为0-1变量

设物流供应商共有s个物流能力状态，hik表示物流供应商i的第k个能力状态的物流供应能力，k=1,2,…,s。物流供应商i处于第k个能力状态的概率为 pik，则供应商i完成xi单位的物流任务的可靠度为，LSSC完成该任务的可靠度为

另外，供应商的满意度也是需要考虑的重要因素。设物流供应商i的满意度为Hi，等于分配到的物流量xi除以其平均物流能力，即则系统满意度为其中 βi表示集成商对物流提供商i的偏好程度，且满足

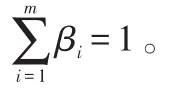
物流服务供应链订单任务分配问题可以归结为下列优化问题：选择一组中标企业集合，以成本最小、可靠性和满意度最大为评价准则，所确定优化模型如下：

模型Ⅰ：

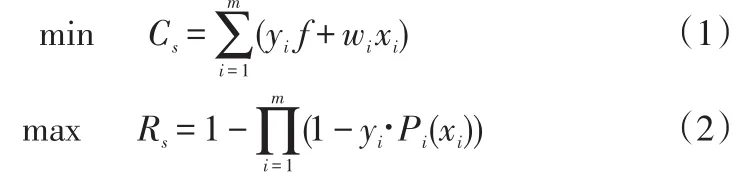
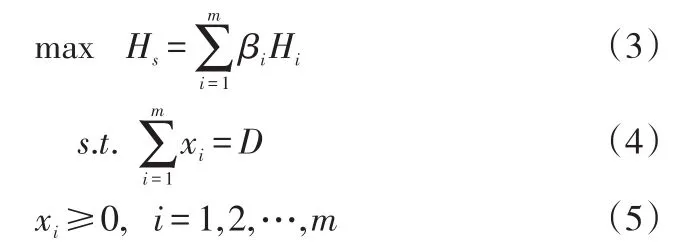
约束条件（4）要求物流任务分配量必须等于订单量。约束条件（5）是物流任务分配量的非负约束。

3 遗传算法求解

众所周知，线性整数规划问题是NP-hard问题，求解该问题的精确解算法具有指数复杂性。因此，线性整数规划问题的近似算法和演化算法近年来得到快速发展。而非线性规划问题则更加困难。遗传算法是演化算法中较好的一种，近年来在各个领域中得到广泛应用，本文采用遗传算法对其进行求解。

3.1 目标函数的处理及适应度函数的选取

上述模型是一个多目标规划问题（Multi-objective opimization）。由于多目标规划问题中各目标之间存在着相互冲突和不可公度性，很难找到一个绝对的最优解，因此，通常采用的方法是在各目标之间进行折衷，以得到Pareto最优解。目前，关于多目标确定性问题，已有专门的求解方法，如评价函数法（线性加权法、参考目标法、极大极小法）、目标规划法、分层序列法、交互规划法、隶属函数法等。该模型的求解按如下思路进行：先将目标函数（1）转化成约束条件，再利用线性加权和法将目标函数（2）和（3）合称为一个单目标，从而将多目标规划模型转化为单目标规划模型。

首先通过引入关系成本系数的方法，将Cs转化为Cs≤(1+δ)，其中，为Cs的最小值，δ为一个较小的正数。这种处理方法表示在进行LSSC任务分配时，不以追求成本最小化为目标，而只是要求将成本限制在一个合理的范围内即可。然后通过线性加权法将式（2）和式（3）合成一个新的max型目标函数，此时的模型为：

模型Ⅱ：

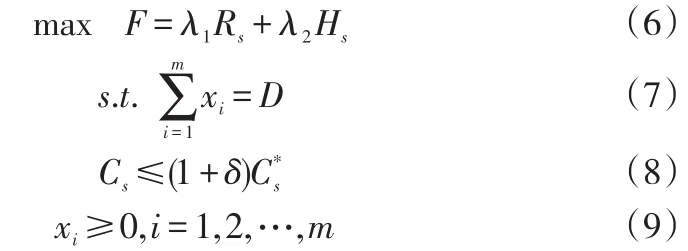
式（6）为模型Ⅱ的目标函数，其中λ1，λ2分别为系统可靠性Rs和任务分配总体满意度Hs在多目标优化问题中的重要程度，可由决策者主观决定。算法直接采用目标函数（6）作为适应度函数。

3.2 编码方案及算法规则

常用的个体编码方式有二进制、格雷码、浮点数（实数）三种。为了解码方便及提高运算速度，采用整数编码方案。

由于模型中包含成本约束和需求约束，所以合法父代染色体经遗传算子操作后可能产生违反约束的无效染色体。针对约束条件的处理，常用的策略主要有拒绝策略、修复策略、改进遗传算子策略和惩罚策略等。根据该模型的特点，本文采用修复策略。其中修复算子采用启发式规则对无效染色体进行修复。修复的步骤：首先检查染色体是否满足各子任务需求等式的约束，根据单位物流服务价格的大小对决策变量进行排序，对某项子任务，分配量若超出订单量，则减少单位物流服务价格最大的决策变量的值（若值不为零），若减少到值为零仍不满足约束，可减少下一个单位物流服务价格较大的决策变量（若值不为零）的值，直到满足需求等式约束为止；若分配量少于订单量，则增加单位物流服务价格最小的决策变量的值（增加后的分配量不能超出其能力），否则，可增加第二个单位物流服务价格较小的决策变量的值，直到满足需求等式约束为止。其次，检查染色体是否满足总成本约束，若总成本超出预期值，可减少单位物流服务价格最大的决策变量值（若不为零），而同时增加相同数量的单位物流服务价格最小的决策变量值，直到满足成本约束为止。采用这种方法，一个不可行解不仅能得到快速修复，而且在被修复的同时还能被推进到解空间中一个局部较优的位置，进而提高计算结果的准确性和效率。

算法流程如图1所示。

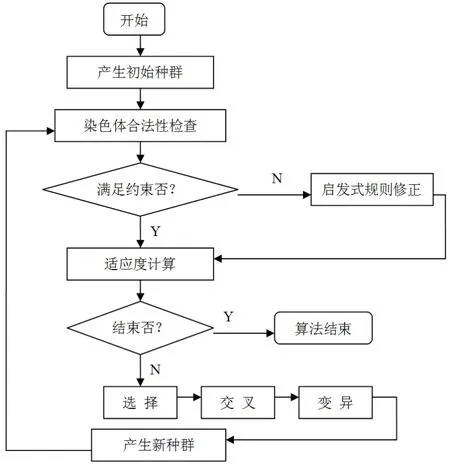
图1 LSSC订单分配算法流程图

3.3 复制、交叉和变异算子

复制算子采用轮盘赌（roulette wheel）选择，即个体被选中进行复制的概率与该个体的适应度大小成正比[12]。交叉操作采用常用的两点交叉，变异操作采用均匀变异。根据适应度值动态地确定调节遗传操作的交叉概率和变异概率。

4 算例仿真

设物流服务集成商有一物流运输任务需外包给其他物流供应商完成。物流任务量为110TEU（Twenty-feet Equivalent Uint）。现有6个物流供应商参加投标。若集成商与某物流商合作，则合作的固定成本均为1 000USD，总成本约束为33 000USD。各物流供应商的物流能力状态及投标价格见表1。集成商面临的问题是如何将订单任务分配给合适的物流供应商使得任务完成的可靠性最大、供应商的满意度最大、任务完成的总成本最小。

算法用Matlab编程实现，编码为整数编码（取值范围为0到各物流提供商的最大物流能力），1条染色体中有6个决策变量。设置目标权重λ1=λ2=0.5，种群规模80，交叉概率取0.8，变异概率0.2。计算后得近似最优解x*=[9 38 24 6 33 0]，即物流任务分配给五个物流供应商共同完成，此时订单完成的总成本为Cs=32 690，完成该任务的可靠度Rs≈0.999 9，总体满意度Hs=0.454 3。

显然，若目标函数只考虑成本最小化，最优解只需将订单任务分配给两个物流供应商（1和2，或2和5）即可，而此时可靠度和满意度都没有达到最优。只考虑成本因素的订单任务分配方案既不利于与物流供应商的长期合作，也会影响客户的满意度。

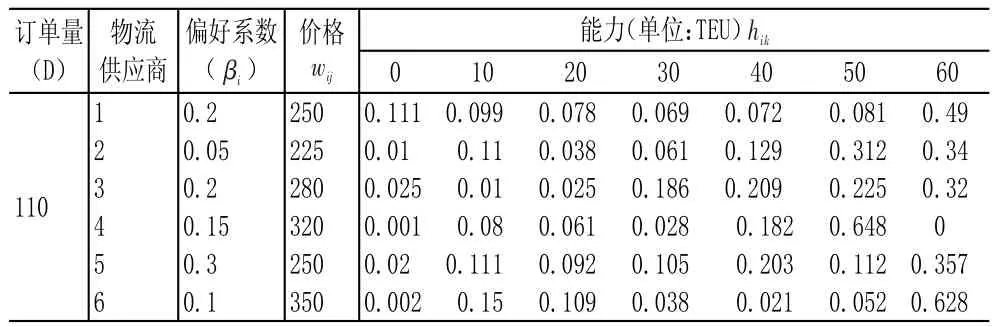
表1 集成商物流订单量与提供商物流价格和能力分布

5 结论

考虑了物流供应商物流能力随机条件下物流订单任务的分配问题。建立了基于多种物流能力的任务分配模型，给出模型的求解方法，并对订单任务分配模型进行了算例分析。由于受多种因素影响，物流供应企业物流能力存在随机性，进而影响物流任务完成的可靠性。物流集成商在进行订单任务分配时，不仅需要考虑成本因素，还需考虑供应商满意度和物流任务完成的可靠度。

[1]李阳珍,张喜征.基于Markov过程的物流服务供应链可靠性分析[J].重庆交通大学学报(自然科学版),2012,(4).

[2]Gerard J Bruke.Sourcing Decisions with Stochastic Supplier Reliability and Stochastic Demand，Production and Operations Management Society,2009,18(4):475-484.

[3]陈香,龚本刚,胡朝忠.面向LSSC可靠性的制造商威胁度多属性评估模型[J].统计与决策,2012,(8).

[4]刘伟华,季建华,周乐.两级物流服务供应链任务分配模型[J].上海交通大学学报,2008,(9).

[5]张德海.物流服务供应链的故障树分析及优化[J].统计与决策,2009, (14).

[6]姜意扬,王勇,邓哲峰.基于LSSC的供应商选择与订单分配[J].工业工程,2011,(6).

[7]陈玉镇,赵一飞.基于模糊优化的物流服务供应链任务分配研究[J].中国经贸导刊,2012,(1).

[8]程建刚,李从东.一种新型物流服务供应链建模方法[J].工业工程, 2009,12(1).

[9]李姗姗.物流服务供应链订单分配优化及其遗传算法[J].运筹与管理,2014,23(5).

[10]范琛,王效俐,陈瑾,张露.信息更新下的物流服务订单分配[J].同济大学学报(自然科学版),2014,42(9).

[11]黄小原.供应链模型与优化[M].北京:科学出版社,2004.

[12]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,2002.

Study on LSSC Task Allocation Model and Algorithm under Stochastic Logistics Capacity

Wu Xiaoyan1,2,Lu Shichang2,Liu Zhongmin1
(1.School of Management,Jilin Normal University,Siping 136000; 2.School of Business Administration,Liaoning Technical University,Huludao 123000,China)

In this paper,considering the randomness of the logistics capacity of the functional logistics service providers(FLSP),we built the corresponding logistics service and supply chain order allocation model,introduced its solution,and at the end,presented a numerical analysis.

logistics capacity;random condition;logistics service and supply chain;order allocation;genetic algorithm

F252；F224

A

1005-152X(2015)10-0091-03

2015-07-25

吉林省社会科学基金项目（2015BS5）

吴晓研，吉林师范大学管理学院讲师，辽宁工程技术大学在读博士，研究方向：物流与供应链管理；路世昌，辽宁工程技术大学工商管理学院教授，博士生导师，研究方向：战略管理、供应链管理；刘忠敏，吉林师范大学管理学院副教授，博士，研究方向：技术经济管理。

10.3969/j.issn.1005-152X.2015.10.026