基于TEI@I方法论的防城港港口吞吐量预测

范林胜，邓建新,2，闵 浩，张 琦

（1.广西大学 制造系统与先进制造技术重点实验室，广西 南宁 530004；2.广西大学 机械工程学院，广西 南宁 530004）

基于TEI@I方法论的防城港港口吞吐量预测

范林胜1，邓建新1,2，闵 浩1，张 琦1

（1.广西大学 制造系统与先进制造技术重点实验室，广西 南宁 530004；2.广西大学 机械工程学院，广西 南宁 530004）

针对防城港港口吞吐量的波动趋势，基于TEI@I方法论，提出一种预测防城港港口吞吐量的框架。采用多元线性回归拟合其线性特征，采用三层BP神经网络模型拟合其非线性特征，并将其结果集成相加得到防城港港口吞吐量的预测模型。实际预测结果表明，这种预测方法有较高预测精度，优于单一的预测方法，平均绝对百分比误差从9.33%下降到1.52%，该方法可为未来防城港的发展规划提供数据支撑。

TEI@I方法论；多元线性回归；BP神经网络；防城港；港口吞吐量；预测

1 引言

防城港位于广西南部北部湾北岸，是全国19个枢纽港之一，地处中国—东盟自由贸易区、泛珠三角经济圈和广西壮族自治区北部湾经济区的结合部，现与世界80个国家的220个港口通商通航。随着北部湾经济地位的提升、中国—东盟自由贸易区的进一步发展以及“一带一路”的推进，防城港对于西南地区通往东盟和海外各国的大通道将发挥越来越重要的作用。当前经过防城港港口的经济贸易往来更加频繁，在2014年，防城港港口的吞吐量为1.15万t，同比增长8.9%。随着该港口的物流吞吐量迅猛增长，运输能力不足、货物压港严重等问题日渐凸显，同时，港口吞吐量对周边地区的经济发展也十分重要，在很大程度上能影响一个地区的投资方向和经济走向。因此，急需科学有效地预测和分析其港口吞吐量，以实现优化调度和资源配置、促进运输系统的高效运作，为港口规划建设、确定港口投资规模提供重要决策信息，从而提高投资效益，促进港口及其所在城市的发展和经济增长。

针对港口吞吐量的预测，国内外学者开展了大量类似的研究，得到了丰富的研究成果，涉及港口吞吐量、集装箱量、物流需求量等，提出了多种预测方法或模型，但还鲜见对防城港吞吐量的预测。王景敏等[1]采用三次指数平滑法预测了广西北部湾港口物流需求；J.G.de Gooijer等[2]使用多变量时间序列模型预测了安特卫普港的交通流量；Chien-Chang Chou[3]运用修改的回归模型预测了台湾进口的集装箱量；C.H.Wei等[4]使用人工神经网络研究预测了高雄港的集装箱量；M.T.Chou等[5]应用SARIMA模型分析了高雄港的集装箱量；C.I.Hsu等[6]应用灰色模型预测了航空货运业务数量；Xiao Jin等[7]运用粒子群算法预测了转移集装箱吞吐量；Shih-Huang Chen等[8]采用遗传规划预测了集装箱吞吐量；侯宝燕[9]基于组合预测方法预测了营口物流需求量；黄俊聪[10]基于组合预测方法预测了福州港物流需求量；许利枝等[11]基于TEI@I方法论预测了青岛港口的货运量；Huang Anqiang等[12]使用混合模型预测了青岛港口集装箱吞吐量；Gang Xie等[13]基于LSSVR的混合模型预测了集装箱吞吐量。传统的线性回归和时间序列预测方法虽然易于操作而且简单，但是预测精度很难达到要求，智能算法在一定程度上能达到预测的精度，但预测对参数十分敏感，很难就有稳定性。TEI@I方法论在处理具有高度波动性和复杂系统的预测问题上（例如原油价格、汇率），取得了很好的预测效果。

港口吞吐量受港口所在区域的经济产业发展的多种因素的影响，具有高度的波动性、复杂性和不确定性，表现出很强的线性和非线性特征。图1所示为防城港1990-2013的吞吐量数据，在1990到2004年这段时间，吞吐量增长速率较稳定，表现为一定的线性关系，从2005到2013年增长速率不稳定，表现为非线性关系，单独运用线性和非线性模型进行预测，误差都较大，如对图1中的数据应用指数模型预测，平均相对误差在9%左右。为了更准确地预测其吞吐量，本文引入TEI@I框架，定量地分析港口吞吐量的线性和非线性部分，以提高对港口吞吐量的分析能力和预测能力。

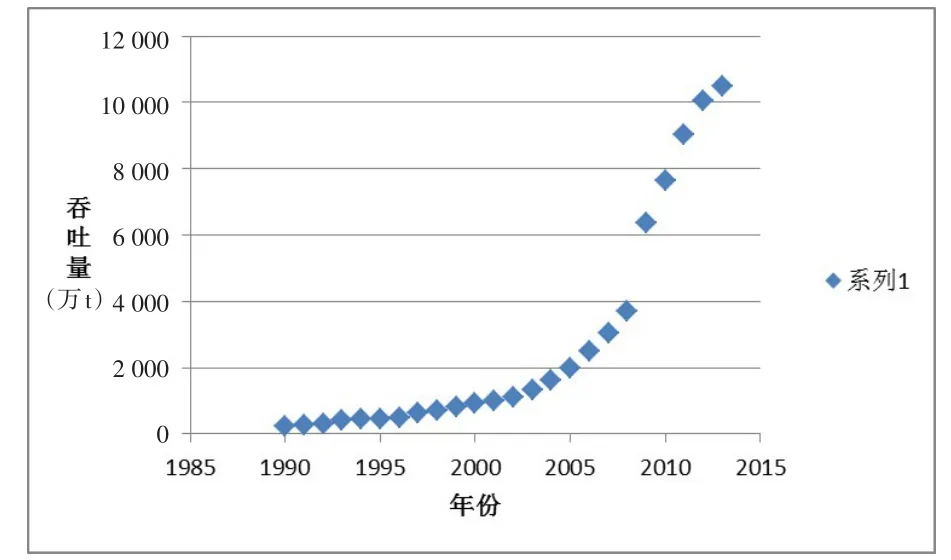
图1 防城港港口历年吞吐量

2 基于TEI@I方法论的港口吞吐量预测框架

TEI@I方法论是汪寿阳等[14]提出的一种针对具有突现性、不稳定性、非线性和不确定性等特征的现实复杂系统进行分析的全新研究方法论。该方法基于先分解后集成的思想。首先，用计量经济模型预测线性部分，其次，用人工智能方法，如BP神经网络拟合非线性部分；然后，利用专家预测系统来量化重要事件的影响结果；最后，集成三者的结果，得到一个综合的预测数据。

然而，对于影响防城港港口吞吐量不规则的事件，如因北部湾经济区的批准、政府加大投资等，处理难度较大，且不易量化，很难预测，因此，本文暂不考虑不规则事件对吞吐量的影响，即只基于防城港吞吐量线性和非线性部分进行集成预测，得到一个综合的预测数据。本文建立的基于TEI@I方法的防城港港口吞吐量集成预测框架如图2所示。

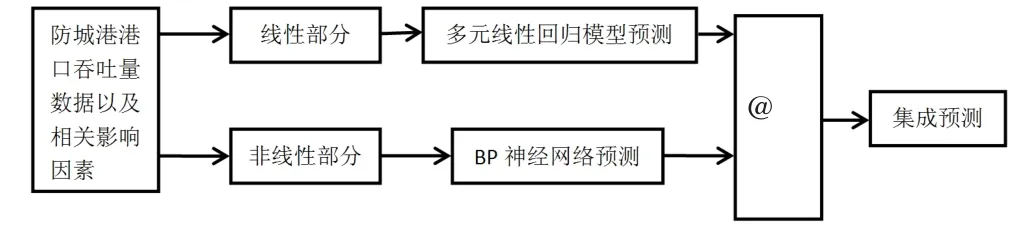
图2 防城港港口吞吐量集成预测框架

设防城港港口每年的吞吐量实际数据为{Yt，t=1，2，3，...}。综合考虑数据的可得性和对防城港港口的实际考察，影响防城港港口吞吐量的可能因素有：防城港市的第一产业总值、第二产业总值、第三产业总值、全年固定资产投资、社会消费品零售总额、进出口总额等。因此，首先用多元线性回归来拟合防城港港口吞吐量的历年数据，产生一个新的预测序列，记为{}：

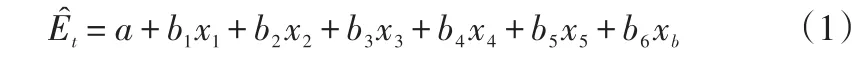
式（1）中，x1表示防城港市的第一产业总值，x2为第二产业总值，x3为第三产业总值，x4表示全年固定资产投资，x5表示社会消费品零售总额，x6表示进出口总额，a和bi（i=1，2，…，6）是需要确定的预测参数。

通过分析{Yt}和{}序列，可以得到防城港港口吞吐量的误差序列，记为{et}。

在此基础上，应用三层的BP神经网络来拟合得到的误差序列，如图3所示，即包含1个输入层、1个隐含层和1个输出层，每层都有若干个神经元组成，神经元的传递函数为S型函数，输出量是0到1之间的连续量，权值的调整采用反向传播（Baekpropagation）学习算法，每个输入都通过一个适当的权值W与下一层相连，网络输出表示为a=f(WP+c)。其输入层为式（2）得到的误差序列，输入层的节点个数N，需要根据误差序列数量的多少来确定，一般不少于3个，如果序列数据量大，输入为3个以上。输出层为预测得到的吞吐量新误差，该吞吐量新误差仍然是一个时间序列，记为{}。

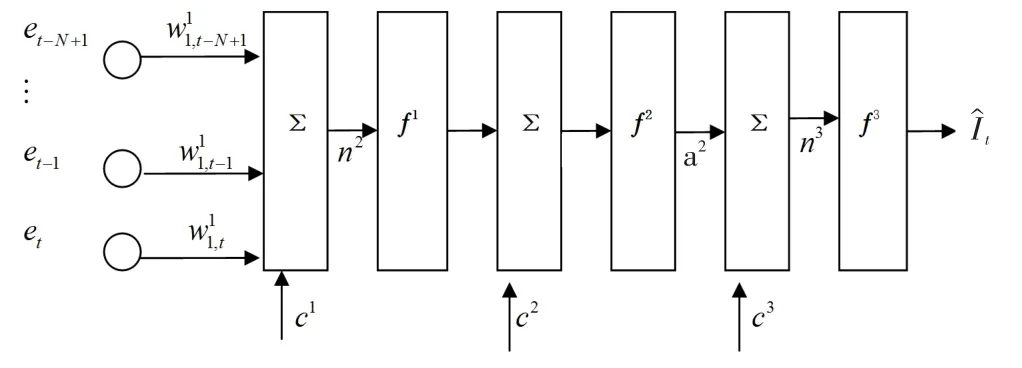
图3 三层BP神经网络模型

用三层BP神经网络拟合得到的吞吐量误差序列仍然是一个时间序列，记为{}。实际上{}是一个非线性函数，根据图3可以表示为：

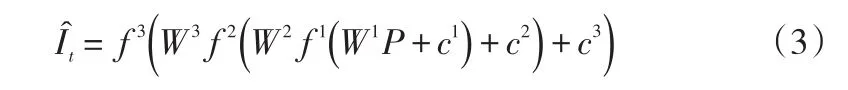
其中 fi为第i层网络的输出值，Wi为第i层的权值矩阵，P为输入变量矩阵，ci为阈值（i=1,2,3）。

根据式（4）确定隐含层数。

式（4）中，N为输入层节点数，L为隐含层节点数，M为输出层节点数，a为0到10之间的常数。

为了评价预测的性能，本文使用平均绝对百分比误差（MAPE）、均方根误差（RMSE）作为评价准则，定义为：

式中D为测试周期。

3 预测分析

3.1 数据来源

综合分析，影响防城港港口吞吐量的可能相关因素为防城港市的第一产业总值、第二产业总值、第三产业总值、全年固定资产投资等。根据广西年鉴及广西统计信息网（http://www.gxtj. gov.cn/tjsj/tjnj）的相关信息，统计得到防城港港口1990-2013年的吞吐量数据及影响吞吐量因素的相关数据，见表1。

表1 影响防城港港口吞吐量的各项经济指标

3.2 预测模型及预测分析

为了建立预测模型和进行验证，以下选取1990-2010年数据进行模型建立，使用2011-2013年的数据为测试样本数据，用于检测预测误差和评估预测精度。同时，为了评估集成预测模型的性能，还将与二次曲线等独立预测方法的预测结果进行对比分析。

3.2.1 二次曲线预测。从图1知，防城港港口1990-2013年吞吐量呈指数发展趋势，可直接建立指数模型进行预测。根据1990-2010年的数据，利用Excel求解，可以得到对应的指数拟合模型为

3.2.2 多元线性回归模型。按照图1所示的框架，首先使用多元回归模型进行防城港吞吐量的预测分析，处理其线性部分的特征。

使用SPSS20，输入1990-2010年防城港市的第一产业总值（x1）、第二产业总值（x2）、第三产业总值（x3）、全年固定资产投资（x4）、社会消费品零售总额（x5）、进出口总额（x6）的数据，作为多元线性回归的训练样本，采用逐步进入的方式，选入P≤0.05，剔除标准P≥0.10得到的进入变量和对应的系数，求解结果见表2、表3。

表2 模型概要

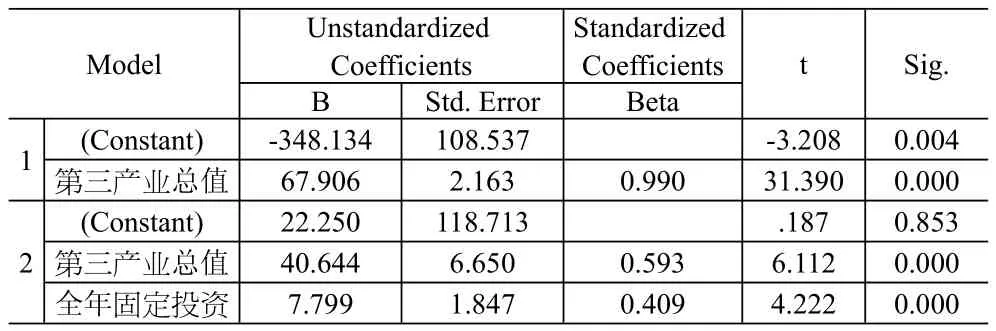
表3 模型系数

从表2可以看出R2为0.990，拟合效果较好，从表3中得到对应多元线性回归模型为：

从模型可以看出，吞吐量主要与第三产业总值、全年固定资产投资直接相关，这与陈涛焘等[15]得出的结论相一致。这是因为防城港及其周边地区第一产业和第二产业一直薄弱，而且需求比较稳定，在1990至2010年前没有大量大型企业投产，产生的需求不大。2012年后，防城港才开始了千亿元产业园的建立，如防城港钢铁项目，但目前这些企业仍未投产，因此对其吞吐量影响不够明显。

把2011-2013年防城港港口的吞吐量作为测试样本，结果见表4。

表4 测试样本的误差值

根据式（1）得到误差序列，将得到的预测误差序列制作成散点图，如图4所示。

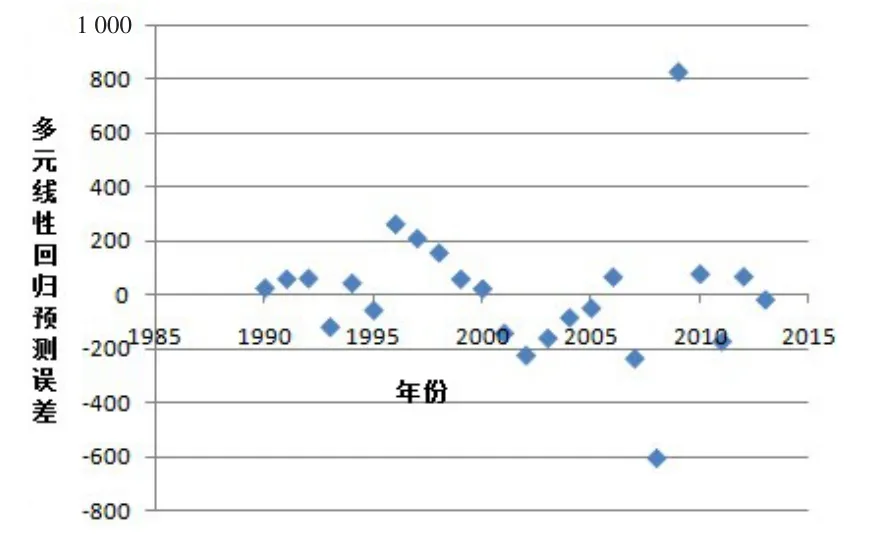
图4 多元线性回归预测误差散点图

从图4中可以看出，得到的多元线性回归预测误差不稳定、呈非线性特征。

3.3 BP神经网络

根据前面已建立好的三层BP神经网络模型，使用Matlab求解计算实现时，首先将得到得多元线性预测值标准化处理，其中e*t为标准化的多元线性回归预测误差值，et为多元线性回归预测误差值，h和g分别是多元线性回归预测误差值中的最大值和最小值，设置学习目标误差值为0.000 1，训练最大次数为2 000次。其它的网络参数确定过程如下：

（1）输入层节点数。由于数据的有限性，确定该实例中的输入层节点为3个，即将相邻三年误差序列作为一组输入数据，如将1990、1991、1992年多元线性回归预测模型的误差序列为第一组输入数据，将1991、1992、1993作为第二组输入等。

（2）隐含层节点数。参考式（4），用逐一试算法确定最佳的节点数，经过试算，该实例预测隐含层节点数为4。

（3）输出层节点数。本文将拟合的误差序列作为输出值，即输出节点数为1。

（4）转换和学习函数。第一层的转化函数选为logsig，第二层的转化函数选为purelin，学习函数选为traimlm。

（5）训练样本集。样本集选为1990-2010年多元线性回归预测模型的误差序列。

（6）测试样本集。测试样本选为2011、2012和2013年多元线性回归预测模型的误差序列。

最后得到以下拟合曲线，如图5所示，其中横轴表示误差序列组，纵轴表示标准化后的预测误差值或者真实值。

从运行结果可以得出，最后3个点的测试平均绝对百分比误差分别为57.55%、24.69%、2.86%，随着样本量的提高，绝对误差会逐渐降低。

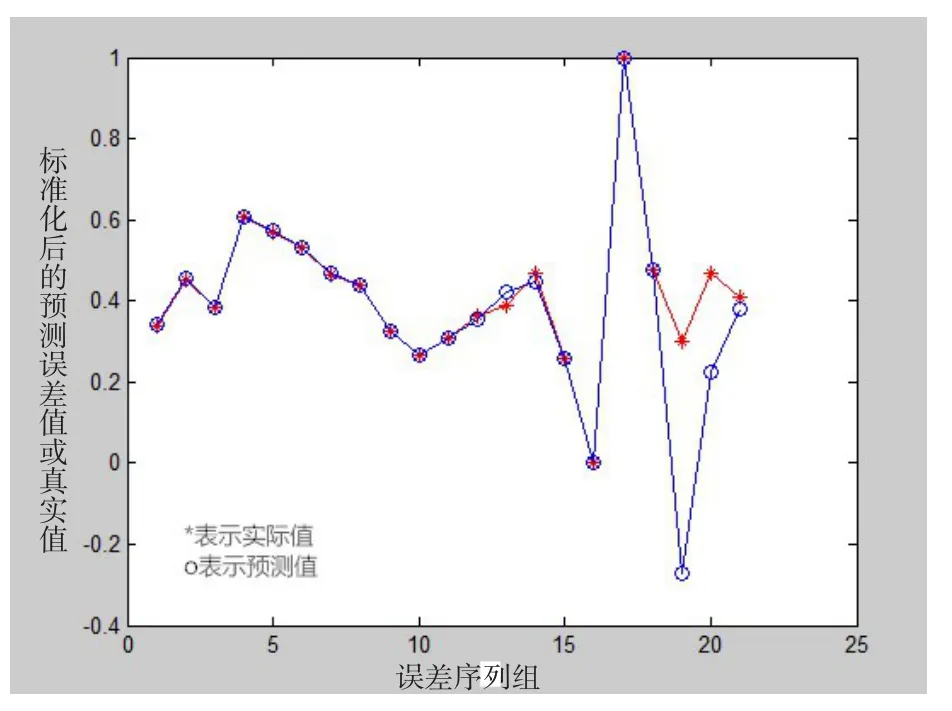
图5 BP神经网络拟合数值与真实值的比较

3.4 综合集成与单一预测比较

将多元线性回归拟合值E^t与BP神经网络值I^t求和，得到综合预测结果Y^t，预测结果见表5。

从表5可以看出，指数回归模型预测、单一多元线性回归预测与集成模型预测的平均绝对百分比误差分别为9.33%、6.78%和1.52%。它们的均方根误差分别为1 058.997、290.35和239.60。无论是预测的准确性还是稳定性,综合集成预测的结果都大大高于单一模型的预测。这也充分说明了集成预测适合防城港港口吞吐量预测。

4 结论

防城港的吞吐量近年不断增加，波动较大，有明显的线性和非线性特征，本文基于TEI@I集成理论框架，提出防城港港口吞吐量的预测模型，模型将吞吐量的线性部分通过多元线性回归进行拟合，非线性部分转化为线性部分的预测误差，通过BP神经网络进行建模预测，该模型框架操作简单，不存在复杂的数据处理。由实际预测可知，目前防城港的吞吐量主要与第三产业总值、全年固定资产投资直接相关，从预测的效果可以看出，所提出的模型可较好地用于防城港港口吞吐量的预测，在平均绝对误差和平方误差上都优于单一的多元线性回归模型和直接的非线性预测，能较好地适应防城港吞吐量的波动趋势，可为港口运营管理和相关部门投资决策等提供更准确的依据。

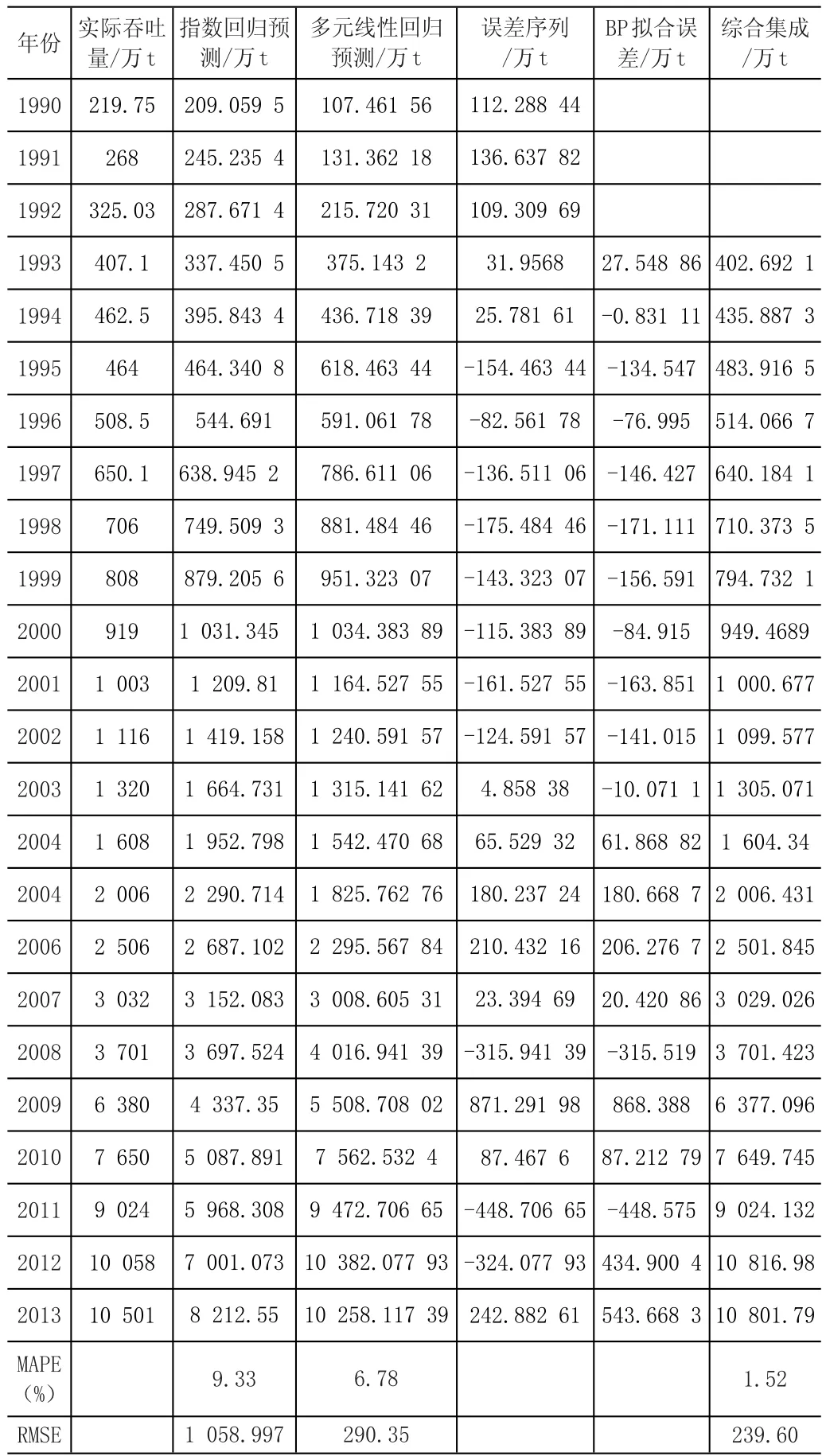
表5 指数回归模型和多元线性回归模型与集成模型的比较

[1]王景敏,朱芳阳,隋博文,等.广西北部湾港口物流需求预测及发展模式研究[J].物流科技,2010,(12):26-28.

[2]Gooijer J G de,Klein A.Forecasting the Antwerp maritime steel traffic flow:A case study[J].Journal of Forecasting,1989,8(4):381-398.

[3]Chou C,C Chu,G Liang.A modified regression model for forecasting the volumes of Taiwan's import containers[J].Mathematical and Computer Modelling,2008,47(9-10):797-807.

[4]Wei C H,Yang Y C.A study on transit containers forecast in Kaohsiung port-applying artificial neural networks to evaluating input variables[J].Journal of the Chinese Institute of Transportation,1999,11(3): 1-20.

[5]Chou M T,Lee H S,Lin K.A study of forecasting the volume of trans and the harbor operation for port of Kaohsiung[J].Journal of Maritime Sciences,2003,12(1):235-250.

[6]Hsu C I,Wen Y H.Applying grey forecast models to predict international air travel demand for Taiwan area[J].Transportation Planning Journal,1997,6(3):525-555.

[7]Xiao Jin,Xiao Yi,Fu Ju Lei,et.al.A transfer forecasting model for container throughput guided by discrete pso[J].系统科学与复杂性（英文版）,2014,27(1):181-192.

[8]Chen S,J Chen.Forecasting container throughputs at ports using genetic programming[J].Expert Systems with Applications,2010,37(3):2 054-2 058.

[9]侯宝燕.基于组合预测法的营口港物流需求预测研究[D].大连:大连交通大学,2013.

[10]黄俊聪.基于组合方法的港口物流需求预测研究[D].福州:福建农林大学,2009.

[11]许利枝,汪寿阳.港口物流预测研究:基于TEI@I方法论[J].交通运输系统工程与信息,2012,(1):173-179.

[12]Anqiang Huang,Kinkeung Lai,Yinhua Li,Shouyang Wang.Forecastingcontainer throughput of Qingdao port with a hybrid model[J]. Journal of Systems Science and Complexity,2015,28(1):105-121.

[13]Xie Gang,Wang Shouyang,Zhao Yingxue,etal.Hybrid approaches based on LSSVR model for container throughput forecasting:A comparative study[J].Applied Soft Computing Journal,2013,13(5):2 232-2 241.

[14]Wang S Y,Yu L,Lai K K.Crude oil price forecasting with TEI@I methodology[J].Journal of Systems Science and Complexity,2005,18 (2):145-166.

[15]陈涛焘,高琴.港口集装箱吞吐量影响因素研究[J].武汉理工大学学报(信息与管理工程版),2008,(6):991-994,1 003.

Throughput Forecasting of Fangcheng Port Based on TEI@I Methodology

Fan Linsheng1,Deng Jianxin1,2,Min Hao1,Zhang Qi1
(1.Guangxi Key Laboratory of Manufacturing System&Advanced Manufacturing Technology,Guangxi University,Nanning 530004; 2.School of Mechanical Engineering,Guangxi University,Nanning 530004,China)

In this paper,in view of the fluctuation of the throughput of the Fangcheng Port,and based on the TEI@I methodology,we proposed a framework for the forecasting of the throughput of the port,built the corresponding throughput forecasting model and through an empirical test,showed that the method could yield more accurate result and reduce the average absolute error from 9.33%to 1.52%.

TEI@I methodology;multiple linear regression;BP neural network;Fangcheng Port;port throughput;forecasting

U691.71；F224

A

1005-152X(2015)10-0075-05

2015-08-25

广西自然科学基金项目“面向资源利用优化的物流业务协同感知模型研究”（2014GXNSFBA118281）

范林胜（1989-），男，广西桂林人，广西大学机械工程学院硕士研究生，主要研究方向：物流工程；邓建新（1979-），男，四川广元人，博士，副教授，主要研究方向：制造系统及其信息学、物流信息学；闵浩（1989-），男，湖北仙桃人，广西大学机械工程学院硕士研究生，主要研究方向：物流作业流程管理和智能化决策系统；张琦（1989-），男，河南信阳人，广西大学机械工程学院硕士研究生，主要研究方向：物流信息化。

10.3969/j.issn.1005-152X.2015.10.022